> Техника, страница 43 > Дифференциальная геомetpия

Дифференциальная геомetpия

Дифференциальная геомetpия, отдел геометрии, изучающий свойства кривых и поверхностей методами анализа бесконечно малых. Д. г. разделяется на теорию кривых, плоских и пространственных, и теорию поверхностей.

Теория плоских кривых. Плоская кривая м. б. задана в декартовых координатах ур-ие.ч У-/(*), (1)

А В

Фигура 13.

или

F(x,y)= 0. (2)

Наряду с этими двумя видами, часто пользуются более симметричным представлением кривой в параметрической форме:

χ=φ(<), у=(3)

При изменении параметра t точка (х, у) перемещается по плоскости, описывая кривую (если f обозначает время, то параметрическ. ур-ия характеризуют движение точки, а кривая является траекторией движения). Па-раметрич. форма является наиболее общей; наир., в этой форме получится уравнение (1), если мы положим: ж=t, y=f{t). В случае уравнения (2) у оказывается, вообще говоря, многозначной ф-ией от гг; при представлении кривой в форме (3) часто удается подобрать для φ и ψ однозначные ф-ии.

II р и м е р. Ур-не окружности в форме (2): х²- -у²=а^г; в форме (I): у=± V а² — х^г; в качестве параметрич. формы можно взять: х — а cos f, у—asm f. Наряду с декартовыми координатами кривая м. б. задана ур-ием в полярных координатах: r=F(<p).

Длина дуг и кривой определяется как предел длин вписанных ломаных, когда длины звеньев ломаной стремятся к нулю. Методами интегрального исчисления доказывается, что этот предел представляется в виде интеграла. Для ур-ий (3) имеем следующее выражение длины дуги s:

т

s=S »V(0J^J + Ш dt,

t.

где 1₀ и Т—значения параметра (, соответствующие началу и концу дуги; отсюда для вида (1), в частности, имеем:

Л

s= J У i. + у^г dx.

U

Для д и ф ференциала д у г и получаем выражение:

ds -- γΐφζηγ + [.7(f)]² dt, или, возводя его в квадрат и замечая, что <p(t) (It dx и φ(ί) dt - dy, получаем:

ds² - dx² + dy². (4)

Последняя ψ-ла справедлива, в какой бы из трех форм ни была задана кривая. Если ур-не кривой дано в полярных координатах, то выражаем х и у через г и φ(χ=τ cos φ и у—т sin т>); дифференцируя эти выражения и подставляя в формулу (4), получаем: ds²=dr² -f r^?d<p².

II p π μ e p. Ценная линия:

X _ X

e" + e ^a j; ds=Vi + y- dx =

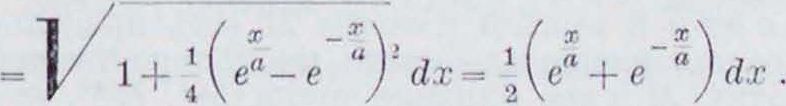
Длина дуги от ж —0 до х=Х:

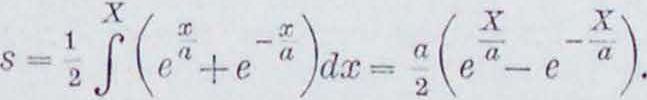
о

У p-и е касательной и нормали. Касательная определяется как предельное положение секущей ММ, когда точка М

неограниченно приближается к М (фигура 1). В дифференциальном исчислении доказывается, что для кривой, заданной в форме (1), угловой коэффициент касательной в точке М равен значению производной:

(5)

Таким образом, ур-ие касательной в данной точке М(х, у) напишется так:

Y-y=?^y-(X-x),

где X, Y—текущие координаты точки на касательной. В случае параметрической формы dy _ у>(0 _ dx p(t)

Нормалью называется прямая, проходящая через точку прямой перпендикулярно к касательной в этой точке. Ее ур-ие:

X-x + %{Y-y)=Q.

В Д. г. определяются отрезки касательной MQ и нормали MR от точки прикосновения до пересечения с осью абсцисс (фигура 1):

; MR-г/~1+ (§). dx

Г

У1 1 +

о

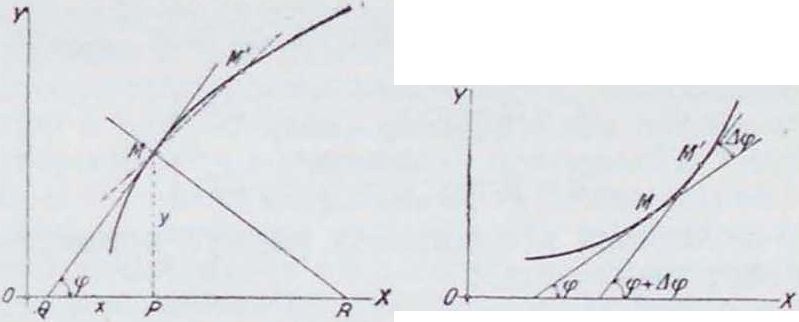
Проекции этих отрезков на ось абсцисс носят названия: QP—п о д к а с а т е л ьн а я, PR—поднормаль. Их выражения таковы:

QP=!, PR =у‘‘^у

^с dy “ dx

dx

Предельное положение касательной, когда точка прикосновения удаляется по кривой в бесконечность, есть асимптота (смотрите Асимптотическое прибли-жепие). Методами

Фигура 2.

дифференциальной геометрии исследуются выпуклость и вогнутотп (смотрите) плоской кривой и в связи с этим точки перегиба, а также особые точки кривой.

К р и в и з н а плоско и к р и в о й. Кривизну можно рассматривать как меру укло-неииякривой от касающейся ее прямой. Проводим касательную к кривой в точке М(х, у) (фигура 2); берем близкую точку кривой М; касательная в ней образует с первоначальной касательной угол λφ пусть длина дуги

ММ есть As. Отношение ~^чх назовем сред-

п е и к р и в и з н о и кривой на дуге ММ. Когда точка М неограниченно приближается к М, отношение ^ стремится к пределу К К - - 7 есть к р ивизяа к р и-

вой в точке М. Если произведем это вычисление для круга радиуса г, получим

К=“; для прямой, очевидно, в каждой точке К=0. Для вычисления кривизны в общем случае замечаем, что φ=arc tg

dy

dx

ИЗ

формулы (5), ds=|/dx -f dy¹ из ф-лы (4), откуда дифференцированием находим: jr _ dxd*y - d*xdy (Λс“+ dy)¹!

Эта формула принимает более простой вид, если кривая задана ур-ием (1); тогда d²x=0, и мы имеем:

Замечаем, что в точке перегиба (?/"=0) имеем К=0. Обратную кривизне величину называют радиусом крив и зны:

1 _ _ (dx+dy)¹

К ~ ⁴ ~ dxd*y - cPxdy

Центр кривизны кривой в точке Ы есть точка С, которая получится, если отложить на нормали в направлении вогнутости кривойотрезокМС.рав-ный радиусу кривизны.

Круг с центром в С и с радиусом МС называют с о п р и к а сающимся кругом; его можно определить и независимо от кривизны,—как о--иредельное положение окружности, проходящей через точку М и две близкие к пей точки кривой, когда эти последние неограниченно приближаются к М. Координаты (с, η)центра кривизны даются ф-лами:

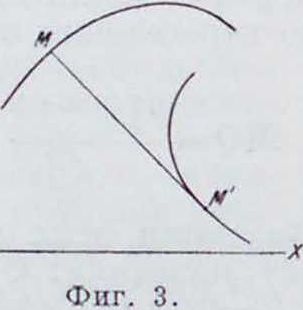
ξ=х-

1 + у"· у"

У,

1 + у“ V ’

(6)

если кривая задана в виде (1), причем у= ф. > У"— · В общем случае имеем:

ξ=χ-п=у+

dx* + dy* dxd*y - d*xdy dx*+dy* dxd*y - d*xdy

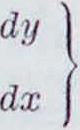
6)

В полярных координатах радиус кривизны имеет выражение:

(Г* г·)· г- + 2г"· - гг" ’

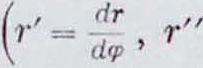
dr

d<?)

Пример. Найти кривизну К параболы у^г=2рх. Дифференцируя, находим: уу =

= р; У² + у"= 0, откуда ν=ζ, ν"=-ζ,· Кривизна

К____ ^р‘.=- *.

!/*(l + Щ¹* (У’:+ V-)^U

Для радиуса кривизны в вершине (t=0) получаем: (<= — р. Центр кривизны лежит в точке (р, 0).

Эволютой кривой называют геометрии, место ее центров кривизны. Рассматривая в ур-иях (G) точку кривой (х, у) как переменную (х—независимое переменное, у—его данная ф-ия), имеем выражения координат (с,р) точки эволюты в функции х, играющего роль параметра. Это и есть параметрические уравнения эволюты. Геометрическое свойство эволюты состоит в том, что: нормаль к кривой в точке М(х,у) (радиус соприкасающегося круга) есть касательная к эволюте в соответствующей точке Μ(ξ,η) (фигура 3).

Первоначальная кривая по отношению к эволюте называется эвольвентой.

П р и мер. Эволюта параболы х²=2 ру,

имеем:?=“; у"=¹. Уравнения (6) принимают следующий вид:

X-,

?>*

J> ’ ^ 2J)

р’. 3.V

⁼ Р + 2_Р

Исключая х, находим:

tffo-P)’·

Теория пространственных кривых. Кривая в пространстве м. б. задана двумя ур-иями между х, у, z как пересечение двух поверхностей: 1< х, у, г) — 0, Ф(х, у, г)=0. Более симметрично представлять пространственную кривую тремя уравнениями в параметрической форме:

®=<К0> 2/=Ψ(0, СП

Для квадрата дифференциала дуги пространственной кривой имеем выражение:

ds²=dx¹ + dy- + dz². (8)

Касательная к пространственной кривой в точке (х, у, г) определится как предельное положение секущей через точки кривой (х, у, z) и (х + Дх, у+Ху, г+Дг), когда вторая точка неограниченно приближается к первой. Уравнения касательной имеют вид:

X - х _Ύ - у Z - z х‘ y’ z’ ’

где X, Y, Z—текущие координаты, х, у, z—значения производных но параметру ( от х, у, z, определяемых формулами (7). Обозначая косинусы углов касательной с осями координат через а, β, γ, находим для них выражения:

X_ β ₌ _у’

а —

I я^,+ у^, + г“

V

У — -

V х“+ у‘‘+ z’·

Если взять за параметр длину дуги, эти формулы примут вид:

_ dx „ _ ily dz

^а ~ ds ’ Р ds ’ ^ ds

Плоскость, проходящая через точку кривой перпендикулярно к касательной, называется нормальной плоскостью. Ее уравнение:

а(Х - х) + β(Υ - у) + γ(Ζ - z)=0.

Всякая плоскость, проходящая через касательную прямую, называется к а с а т е л ь-ной плоскостью к кривой. Из касательных плоскостей выделяют ту, которая имеет наиболее тесное соприкосновение с кривой; соприкасающаяся плоскость к кривой в точке М есть предельное положение плоскости, проходящей через точку М и две близкие точки Μ, М", когда эти последние неограниченно приближаются к М. Для плоской кривой соприкасающаяся плоскость есть та, в которой лежит кривая. Всякий перпендикуляр к касательной прямой в точке М называется норм а-лыо к пространственной кривой; в частности, нормаль, лежащая в соприкасающейся плоскости, называется главной пор-

малью, а нормаль, перпендикулярная к этой плоскости, — бинормалью. Наконец, касательная плоскость, перпендикулярная к бинормали, называется спрям-л я ю щ е и плоскость ю. Кривизна пространственной кривой, как и плоской, характеризует меру уклонения кривой от прямой липни и определяется как предел отношения угла менаду двумя бесконечно близкими касательными к длине соединяющей их дуги. Ее выражение:

*

Наряду с кривизной для пространственных кривых вводится еще вторая кривизна, или кручение, характеризующая степень уклонения кривой от плоской линии. Берем па кривой точку М и близкую к ней Мпусть As—длина дуги ММ и Ду— угол менаду соприкасающимися плоскостями в обеих точках; тогда величина кручения в точке М:

Т=-=Пт

Δν*

Δβ

Связь между производными от направляющих косинусов касательной (α,β,γ), главной нормали (i, m,n) и бинормали (λ,μ,ν) и радиусами кривизны ρ и кручения т устанавливается формулами Серре-Френе:

da I _t dl а λ _л άλ I

US ρ ’ ds ρ τ’ ds τ ’

и еще 6 формулами, аналогичными этим трем, для β и у, m и η, μ и V.

Теория поверхностей. Уравнение поверхности в декартовых координатах дается в виде:

²=/(£,2/). (9)

F(x,y,z)=0. (9)

Возможно также выразить все три координаты точки поверхности в функции двух параметров и, v:

x=*rp{u,v) y=tp(u,v); z=/(u,v). (10)

Из уравнений (10) получается форма (9) в частном случае, когда х=и, у= v, z=f(u,v). Для вычисления дифференциала дуги любой кривой, лежащей на поверхности и проходящей через точку M(x,y,z), в выражение ds²=dx² + dy² + dz²подставляем значения дифференциалов,вычисленные из формул (10), и собираем члены с du², dudv, dv²; получаем: ds²=Edu² + 2 Fdudv + Gdv², (11)

^{где E}= ©² + SO* + ^{и τ}· ^д· Выражение (11) дает квадрат дифференциала дуги любой кривой на поверхности и называется квадратом линейного элемента поверхности. В частности, для поверхности, заданной ур-ием (9), линейный элемент имеет вид:

ds²=(1 + p²)dx² -f 2pqdx dy + (1 + [f)dy², где °*_χ=p,=q. Все касательные к кривым, лежащим на поверхности и проходящим через точку М поверхности, лежат в одной плоскости; эта плоскость называется касательной плоскостью к поверхности в точке М. Уравнение касательной плоскости в случае поверхности, заданной уравнением (9), имеет вид:

Z —2= р(Х -х) + q(Y - у),

где X, Y и Ά—текущие координаты точки плоскости. Перпендикуляр к касательной плоскости в точке касания называется н о р-м а л ыо к поверх н ос т и. Всякая плоскость, проходящая через нормаль, называется нормальною плоскостью; пересечение нормальной плоскости с поверхностью дает кривую, называемую н о р м а л ь-ным сечением поверхности. Исследуя кривизну различных линий па поверхности, проходящих через точку М, мы убеждаемся, что она зависит только от кривизны нормального сечения, имеющего общую касательную с данной кривой, и от угла 0 между плоскостью нормального сечения и соприкасающейся плоскостью кривой в точке ili; обозначая радиус кривизны кривой через с а радиус кривизны соответствующего нормального сечения через R, имеем формулу: с=R cos 0. Это соотношение и составляет содержание теоремы Менье. При исследовании кривизны нормальных сечений, проходящих через данную точку М. обнаруживается, что эта кривизна получает экстремальные значения (наибольшее и наименьшее) для двух сечений, лежащих во взаимно перпендикулярных плоскостях,— главные сечения. Радиусы кривизны ii, и ii₂ главных сечений называются г л а в-н ы м и радиуса м и к р и в и з н ы поверхности в точке М. Выражение ’ + ,! называ-

Н Иг

„ г» 11

ется средней крив и з и ой, а -=- · -=--

IX i IX 2

гауссовой кривизной поверхности. Если ii, и И_г одного знака, то гауссова кривизна положительна в данной точке; радиусы кривизны главных сечений (а поэтому и всех нормальных сечений) направлены по нормали к поверхности в одну сторону; вся поверхность имеет выпуклость, направленную в одну сторону (поверхность лежит по одну сторону касательной плоскости). Если ii, и Д, разных знаков, то гауссова кривизна отрицательна; поверхность вблизи данной точки имеет седлообразную форт-му, то есть лежит по обе стороны касательной плоскости и пересекается ею. Если хоть один из главных радиусов кривизны равен со, то гауссова кривизна равна 0. Точки поверхности, в которых гауссова кривизна положительна, отрицательна или равна нулю, называются соответственно эллиптическими, гиперболическими и параболическим и. Примерами поверхностей положительной кривизны в каждой точке является эллипсоид; отрицательной—однополый гиперболоид, нулевой—плоскость. Шар радиуса R является поверхностью постоянной положительной кривизны; его гауссова кривизна равна. Поверхности постоянной нулевой кривизны называются р а з в е р ты в а ю щ и м и ся поверхностями, т. к. могут быть разогнуты на плоскость; таковы все цилиндры и конусы. Поверхности постоянной кривизны замечательны тем, что на них реально осуществляются свойства неэвклидовой плоскости (смотрите Геометрия), если прямыми называть геодезические линии. Геодезическая линия на поверхности обладает тем свойством, что

27

Т. Э. m. VI.

она является кратчайшей из всех линий на поверхности, которые соединяют две достаточно близкие точки; например: па поверхности шара геодезическими линиями являются дуги больших кругов. Обыкновенно геодезии, линию на поверхности определяют ее геометрии. свойством: это—такая линия, главная нормаль которой в каждой точке совпадает с нормалью к поверхности. Л и и и и кривиз ны поверхности можно определить как такие линии, касательные к которым в каждой точке совпадают с касательной одного из главных сечений. Через каждую точку поверхности проходят две линии кривизны.

. Ium.: Е го р о в Д. Ф., Дифференциальная геометрии, М.—П., 1923; Г у р с а Курс математического анализа, т. 1. М. 1911; Кош теге 11 V. и. К. Allgemeine Theorie d. Raumkurveii и. Flachen. В. 1, 2, В —Lpz. 1921. В. Степанов.