 > Техника, страница 44 > Дифференциальное исчисление
> Техника, страница 44 > Дифференциальное исчисление
Дифференциальное исчисление
Дифференциальное исчисление, отдел исчисления бесконечно ма-л ы х, изучающий свойства производных и дифференциалов от функций.
Производные функции. Пусть задана однозначная и непрерывная ф-ия у—fix), и независимое переменное л получило определенное численное значение. Затем даем л (положительное или отрицательное) приращение Ух; новое значение независимого переменного будет л+Ал, соответственное значение ф-ии будет /(л + Ал). Вычисляем приращение ф-ии Уу=}(х+Ух)—/(л). Из свойства непрерывности f(x) следует, что при безгра-ничном уменьшении абсолютной величины Ал становится бесконечно малым также и Лгу;
по отношение Δ может иметь определенный предел (и действительно имеет его для элементарных ф-ий). Этот предел называется и р о и з в о д и о и но х от у, или от /(л),
и обозначается (л), или у, или ^ (послед-
7 7 ч df(x)
нее произносится: ay по dx), или άχ :
г, V !. fix + Δ») - fix)
/(л)=lim. ·
Δ.ν-И) Δν
Давая л разные значения, получим, вообще говоря, разные значения для производной; производная есть также ф-ия от л.
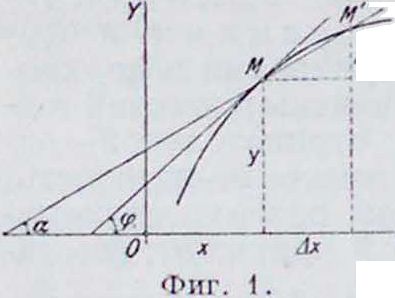
Геометрический сантиметров ы с л и р о и з-водной. У равнение у=/(л) изображает кривую на плоскости; при данном л получаем точку М кривой; значению л + Ал независимого переменного соответствует лу точка М (фигура 1). Из рассмотрения треугольника ММР заключаем, что f!/ есть к tg угла а секущей ММ с осью ОХ. При стремлении Ал к О точка М неограниченно приблткается к М, секущая стремится к предельному положению—касательной ^=tg φ, где <р—угол касательной с осью ОХ. Если производная положительна > (Й, угол φ -острый, ордината кривой увеличивается при увеличении л, ф-ия возрастает; если -~ < 0, угол φ— тупой, ф-ия у бывает (при возрастании л).
Простейшие свойства производной. 1) Производная от постоянной
clc
равна пулю: jv=0 (с—постоянное). 2) Производная от независимого переменного ран-на единице: 3) Пусть и и υ—ф-ин от л; тогда (и· + ν)— и+ ν; производная суммы равна сумме производных. 1) Производная произведения: (и - v)=uv+uv; если один из множителей постоянный, получается более простая ф-ла: (си)=си, то есть постоянный множитель можно вынести за знак производной. 5) Производная частного:
11 “ б) Производная обратной ф-ии.
Пусть у= /(л); л—независимое переменное, у—ф-ия; если это ур-ие разрешить относительно л, получим: χ=φ(;ι); у—независимое переменное, л—функция. Функции /(л) и <р(у) называются обратными одна относительно другой; между их производными существует соотношение:
(!х i , ч 1
, =, НЛП φ (и) —. ·
dy dy ’ γ ·*· (дг)
dx
7) Производная сложной функции. Пусть у — f(u), и=φ(χ), х—независимое переменное; тогда у=/|>(л) I есть сложная ф у н-к ц и я от л. Для производной от у по л имеем выражение:
dy
(tv
dll
(tU
(Iu
dx
П »)
<ρ(αή.
II p о и з в о д н ы е от э л е мент а р н ы х
, Λ
i ί dx ai, _
ψ у н к ци и: /v ^ ах {а—любое постоян ное число, целое или дробное, иоложитель-
d, 1окл е ное или отрицательное); 0. IgaX - χ ; в
d % 1 d г т i d τ ν
частности,. 1ιιχ· --= ;. ах or In а:. ст г
7 ах х 7 dx 7 dx
(e—основание натуральных логарифмов, равное 2,71828.; а—любое положит, число); d d d.
, sin л=cos л;, cos л =— sin л;, te: л
(Λν ’ dx ’ dx °
1. d. 1 d. 1
; -^л=— ; агсэтл^, ;
cos’v dx sin’.x dx у 1 - .ν’
d i d. 1
arc cos л=— ; ar ctg л=;
dx у i - ,v’ dx 1 + ν’
arc ctg л=— 1. На основании пра вил двух последних отделов можем находить производные, то есть д и φ ф e р е н ц и р о-вать любую ф-ию, выраженную при помощи алгебраических действий и символов элементарных функций.
Примеры. 1) у=У —хг. Здесь имеем сложную функцию: у—и“;и=1—л2. По правилу дифференцирования сложной функции («*).(1-**у-1«“*· (_2л)=.
2) у=sin2 Л; здесь у=и2, и=sin л; =
= 2« cos л=2 sin л cos л => sin 2л.
Производные высших и оряд-ков. Мы видели, что производная /(л) от данной функции у - /(л) есть также ф-ия от л. Можно найти производную от /(л); она называется второй производной от /(л); ее обозначения: /"(л), или ^ (читается: d два от у по dx в квадрате). Дифференцируя
/"(х), получим третью производную /"(ж), или -J”, и т. д., наконец, η-ю производную /(п)(х) - Следует отметить частные случаи:
fx, х" - п(п-1)хп
£"нх" — п(п — 1)-··2·Χ=η!,
ипех.,.
iv„ -= ех (для всякого в).
Для η-й производной произведения двух ф-ин существует формула Лейбница:
(ui>)(n)=u(nh + ^i“ y«(r,_1V-f
+(7;)u<n-2V+. +uV™,
где есть биномиальный коэффициент:
/?i ,h n(n-l). (n-ft + 1)
U; ~ ЬП~ 1-2. ft
Дифференциалы фуннций. Производная определяется как предел; из определения предела следует, что переменная отличается от предела на величину бесконечно малую,
следовательно, ^“=/(ж) + а, где а — бесконечно мало при бесконечно малом Ах; освобождаясь от знаменателя, находим:
Sy -= /(х)Ах + аАх;
последнее слагаемое есть бесконечно малая высшего порядка сравнительно с Ах; отбрасывая его, получим выражение, отличающееся от А у на бесконечно малую высшего порядка; это выражение назовем д и ф ф e р е и-н малом от у и обозначим dy. Итак, dy== /(х) · Ах. Полагая, в частности, /(х)=х, найдем: dx 1 · Ах - Ах. После этого можем написать: dy - j(x)dx.
II р и м е р ы: d sin х - cos х dx; d(x") =
- vxn~ dx.
Таким образом, обозначение ^ для f(x)
можно рассматривать как частное дифференциалов от у и х. Так как dx Ах, то можно считать dx постоянным или переменным (в частности, бесконечно малым), но но всяком случае независимым от х; итак, dy есть функция от двух независимых между собой переменных х и dx. По всех приложениях мы можем заменять приращение функции А ее дифференциалом dy, так как на результат последующего перехода к пределу (производная пли интеграл) не повлияет отброшенное бесконечно малое высшего порядка. Если х есть независимое переменное, то легко найти дифференциал от dy, или второй дифференциал от у, при этом мы должны рассматривать dx как постоянное: получаем:
d(dy) - d‘y=[f"(x)dx]dx f"(x)dx“. Аналогично, d3y f”(x)dxi и т. д.: d2y читается: d два от у и обозначает 2-й дифференциал; dx2 есть квадрат дифференциала dx [следовало бы его писать (dx)2]. И случае независимого х имеем d‘X=d(dx)=О, как дифференциал от постоянного.
Замена переменных при дифференцировании. Пусть дана ф-ия у ^ /(х); х—независимое переменное. Тогда можно вычислить ^ и т. д. Затем вводим новое независимое пере менное (, например, x=cp(t) У становится ф-ией от I н имеет производные.
Требуется выразить производные от у по х через производные от у по ί; имеем: -jj- =
dy dx
dx di > 0ТКУДа
dy fix
•ly
di
dx
dt
Применяя эту формулу уже не к у, а к получим выражение 2-й производной:
d-y _ d Id у _ d dx2 dx dx) dx
dy
dx
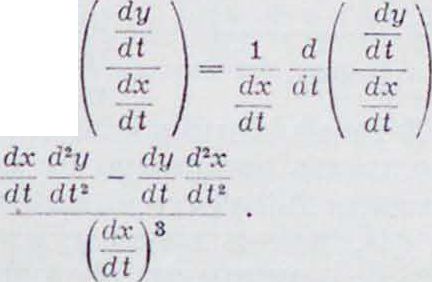
Тем же путем получим выражения для дальнейших производных. Пусть, в частности, повое независимое переменное есть у, тогда,
как мы уже видели, d£=; вычислим вы-
dy
ражение 2-й производной:
d‘y 11 dy _ d i
d.v’ dx dx)
d!.v dy1
IS)·
II p и μ e p. Пусть замена переменного есть
)== 1 ____
·ι ν I dx Ι dx dyl dx J
dy dy dy
тогда
d.v dt ‘
-td
dt
,pt. dy _ p-tdj). fl’y d (
1 dx dt * dx2 dx dl)
-Itd’y _ tidy
«dt· e dt [dt1
idll _ dy [dt: dt)
Теоримы Ролля. Лагранжа и Коши. Т е о-
Р е м а Р о л л я утверждает: если /(х) всюду в интервале (я, Ь) имеет производную и если
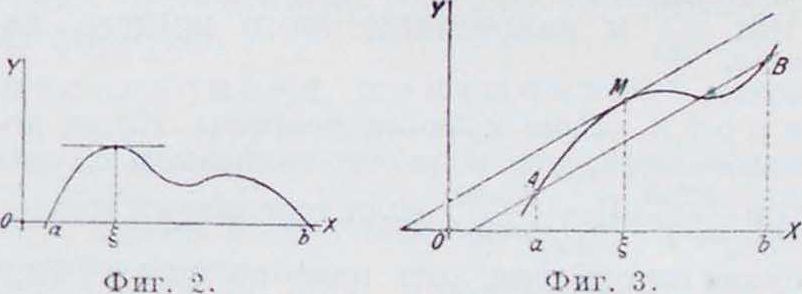
/(а)=0, /(b)=0, то найдется точка 2 этого интервала, в которой значение производной равно нулю: /(£)=0. Геометрии, смысл этой теоремы: если кривая y=f(x) пересекает ось абсцисс в точках а и Ь, то в некоторой промежуточной точке касательная параллельна оси абсцисс (фигура 2). Теорема· Лагра н-ж а, или теорема о конечном приращении, утверждает: если /(х) имеет производную всюду в интервале (а, Ь), то найдется внутри его такая точка с что =· f(£)· Геометри чески это означает, что на дуге кривой у=—/(х) между точками А и В найдется точка М, касательная к которой параллельна секущей А В (фигура 3). Очевидно, теорема Ролля есть частный случай данной. Теорема Коши: если две функции /(х) и у(х) дифференцируемы в интервале (а, Ь) и их производные не обращаются одновременно в нуль, то найдется точка ί интервала (а, Ь), для которой имеет место след, равенство:
/(ί>)-На)
. Г (!) <p(i)
<p(b)—<p(a)
Теорема Лагранжа является частным случаем этой, когда <р(х)=х.
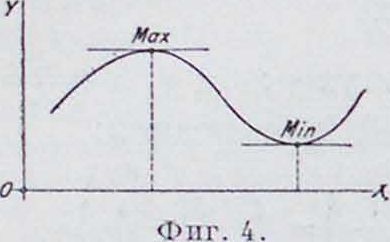
Максимум и минимум функций. Ф-ия /(ж) имеет в точке ж0 м а к с и м у м (относительный), если ее значения для всех достаточно близких точек меньше, чем значение /(ж0); если же все значения ф-ии в близких точках больше ее значения в точке ж0, то она имеет м и н и м у м (относительный) приж=ж„. Необходимое условие максимума или минимума в точке ж0 есть обращение производной в этой точке в нуль (фигура 4). Для того чтобы отличить максимум от минимума, исследуют знак 2-й производной; если /(ж0)=0 и /"(ж) < 0, имеем максимум; если /(ж„)=0 и /"(ж)>0,—минимум. В случае /"(ж0)=0 надо исследовать производные высншх порядков.
II р и м е р. Найти максимум и минимум ф-ии /(ж)=2ж3—9ж2+12ж—3.
Находим /(ж) и приравниваем ее нулю: Сж2—18χ + 12=Ό. Отсюда находим значения ж=1, ж=2, в которых ф-ия может иметь максимум или минимум. Для дальнейшего исследования находим /"(ж)=12ж-18. При ж=1 имеем: /"(1)=— 6(<0)—максимум; приж=2 имеем /"(2)=+6(>0)—минимум. Соответствующие значения функции: /(1)=2; /(2)=1.
Неопределенные выражения. Имеем частное двух ф-ий ; пусть при ж=ж0 и числитель и знаменатель обращаются в нуль: /(ж0)=с/1(ж0)=0; тогда значение ф-ии получает ф и арифметически /(*)
неопределенно. игп и
ψ(χ) нахождение в точке х0 значение форму
Дадим функции Нх) fix)
зовем раскрытием неопределенно ст и. При помощи теоремы Коши доказывается, что в рассматриваемом случае
/(i>=lim Пх)
этого предела на
lim
f(x)
φ-(χ) ·
если последний предел
χ-*χ,τ ж-кг,
существует; если хоть одно из чисел /(ж0), φ(ж0) не равно нулю, мы арифметически получим значение предела [конечное или бес конечное, если 7>(ж0)=0]. Если
= ж0 опять имеет форму 0, применяем тот же
Г(х)
<Р(х)
при ж =
процесс еще раз:
Пример.
Х-+.
cos jc
im ф-НшШи
Т. д. при ж=0 имеет вид
По указанному правилу,
1 - COS X
iim
χ-*-0 О
= Jim
.X->0
sin×2x
опять форма ; применяем правило еще раз:
COS×2
lim. -= Jim
X-+Q M x->0
Если f(x0)=oo, 75(x0)=oc, получаем неопре-
oo
деленное выражение вида — ; правило раскрытия неопределенности остается то же:
Пт=Пт fP; в обоих случаях ж мо-*-*г. *<*> χ->χ.φ <*>
жет стремиться не к конечному значению ж0, а к со. Далее, если /(х0)=0, а ?(ж0)=со, то значение ф-ии /(ж) · φ(χ) принимает неопределенную форму 0-оо; представляя функцию в Нх)
виде, например, -
сводим к первому случаю.
Ψ(χ)
Пример. Пт А-*=Нт д” - Пт 71Л”
Х-*СО Х-*СО С Х-+СО е
,._ п! f,
=.=Пт —= 0.
.ех
Предварительным логарифмированием приводятся к рассмотренным случаям неопределенности: 0°, 1°°, оо°.
Ряды Тейлора и Маклорена. Если /(ж) непрерывна вместе со своими производными (до м-го порядка включительно) в интервале (а,Ь), то для всякой точки ж этого интервала существует равенство:
/(ж)=/(«)
- + V) + h,·
Это—р яд Тейлора с остаточным членом Ii„; для остаточного члена имеем, например, вы ражение:
R.,=
(.V —а)» .(>)
Г (s), где £—некото рое среднее значение между а и ж, а именно ξ=α+Η(χ-α), где 0<#<1. При м=1, как частный случай, получаем теорему Лагранжа. Если для некоторых значений ж остаточный член !£„-*·0, можем для этих значений представить /(ж) в виде бесконечного (сходящегося) ряда Тейлора (смотрите Ряди):
/(ж)=Ко) + Г (а) + (-^>* Г (а) +.
+ («)+.
В этом случае функция /(ж) называется аналитической. В частности, при α= 0, получаем ряд Маклорена:
/(ж)=КО) + * ДО) +. * U Р (0) +.
Приводим разложение некоторых функций в ряд Маклорена:
г -.Х.ЗС“, .Т7“,
6=1 + 1 + 2! + - + л! + —>
.×X“, X* .X7.
sina;=.-3!+l
cos ж=1 —
5!
”. + -Г‘_-? г i! I
2! ‘4! 6! 1 ··
Эти ряды сходятся при всех значениях ж.
П (1 + х)=* -;
+Т-:
(1+жГ=1+™-ж + т(-”,^ж2·
+
т (т - 1) (т - 2)
Ж3
1-2-3
(Последняя ф-ла—обобщенная формула бинома, где т—любое действительное число). Эти два ряда сходятся при [ж | < 1.
Частные производные, полный дифференциал. Пусть дана ф-ия и>=/(ж, у, г) трех независимых переменных ж, у, г. Частной производной οτΜίπο ж называется производная, которая получится, если остальные аргументы рассматривать как постоянные. Ее обозна-
dw Of, ,
0* ’ ИЛИ Wx’ или f*
1 (χ + Δ.Ϊ, у, ζ) - 1(χ, у, г)
чения:
άχ
/i=Iim
Δ.χ-»·0
Αχ
Аналогично определим j и "Jz. Рассуждение применимо к любому числу независимых переменных, большему 1.
Пример:
sin к 9«. sin у - 1
и х > -5t= Sin у X
Ou
ον
- χSH1 y · In a; · cos у.
Беря частные производные от частных производных, получим частные производные 2-го порядка: /Д, /^, и т. д. Имеет место теорема: результат дифференцирования по одним и тем же аргументам не зависит от порядка последовательных дифференцирований. В частности, например, 1”у (х, ?/,.)=f”x (х, у,.). Вторые производные можно записывать также в следующей форме:
ау. f„ ay
IxX Ox* ’ ХУ Vх OxOy ’
Так же определятся третьи производные: оч оч с)3
Ох“ * дх“ду 1 Охду“ ’
И о л н а я производная. Пусть w=—f(x, у, г), где х, у, г—ф-ии независимого переменного ί; w есть сложная функция от t. I Гроизводиая от w по t называется пол и о и производной; ее выражение:
dw д-w dx, Ow dy. du> dz iIt ox dt dy dt dz dt
Производная неявной функции. Ур-ие(®,y)=0 определяет у как неяв-
н у ю ф у н к ц и ю от х; для нахождения -
берем полную производную частей уравнения:
K + F,-%-0,
по х от оиеих откуда
<1у __ _ Fx dx р
V
II о л и ы и д ифференциа л dw функции w=>/(®, у, г) определяется так:
dw - ϋί dx
Ox
а
ay
dy
df, dz;
Oz ’
здесь дифференциалы независимых перемен ных опять можно считать равными их приращениям; доказывается, что dir отличается от полного приращения Дw=f(x +^х. у +
1-Д?/, 2 + Дг)—/(х, i/, г) на бесконечно малую высшего порядка.
Ряд Тейлора для ф-ии двух переменных имеет вид:
fix, У)=/(я, ii) + * ” “ /; (я, i) + ~ я, Ь) + г π (х~а?1гх (а,Ь) + 2(х - а) (у- Ь)/;^ (я, 6) +
+ (У-ЬУОю(", ii)] + · ·
Максимум и минимум функции от двух независимых переменных. Чтобы найти максимум и минимум f(x, у), поступаем след, обр.: приравниваем нулю частные производные 1-го порядка; получаем 2 ур-ия: (х, у)=О, fy (х, у)=0; совместные решения этих ур-ий дают точки, в которых ф-ия может принимать наибольшее или наименьшее значение. Для дальнейшего исследования вычисляем значения вторых производных в точке (а, Ь): /"(я, Ь)=А; /;;/«, Ь)=В; fyy (я. Ь) — С,
составляем выражение В2 —АС; тогда име ем правило: если Вг — АС> 0, в точке (а,Ь) нет ни максимума ни минимума; если же В3—АС <0, то имеем максимум при А < О (и С < 0) и минимум при Л>0 (и С>0). Если же В2—А6’=0, метод не дает ответа.
Пример. f(x, у)=‘дху —х3 — у3. Приравниваем нулю первые производные: Зу — — 3ж2=0, Зж — Зг/2=0. Совместные решения х=0, у=0; ®=1, у= 1. Вторые производные /ii= -6®, /;»=3, Гуу=-Су. Для точки (0,0) В2 — АС=9 ( > 0) пет ни максимума ни минимума; для точки (1,1) В2 — АС= —27 (< 0); А — — 6 ( < 0),—имеем максимум.
Лит.: Г р э и в п л ь В., Элементы дифференциального η интегрального исчислений, ч. 1—’Дифференциальное исчисление, М.—Л., 1928; Ф и л л и н с Г., Дифференциальное исчисление, пер. с англ., М.—Л., 1926; Курса Э., Курс математич. анализа, т. 1, Москва, 1911. В. Степанов.