> Техника, страница 44 > Дифференциальные механизмы

Дифференциальные механизмы

Дифференциальные механизмы, механизмы, в κ-рых результирующее движение пропорционально разности (или сумме) составляющих движений. Наиболее часто применяются на практике дифференциальные механизмы: дифференциал ь-ная зубчатая передача (смотрите Дифференциал) и дифференциал ь ны и блок Вестона (смотрите Блоки).

Дифференциальный в и н т, изобретенный Прони, широко применяется в

		0
Щ	МП! Ш»	t,	—1
	j ¹ г ll	Illi 1	_i
	jvWJWs. iwidlw —у·⁴
		D

Фигура 1.

микрометрах, делительных машинах и фи-зич. приборах (фигура 1). Одним концом с шагом нарезки t винт А ходит в станине С, другим—с шагом t,—в гайке В. двигающейся по направляющим D, D. Перемещения гайки относительно станины определяются из формулы:

i),

где ψ—угол поворота винта относительно станины. Делая разность (<—<,) очень малой, можно получить весьма незначительное перемещение ползуна при значительных углах поворота винта А. При постоянном направлении вращения винта А направление движения ползуна зависит от знака разности ((— <,). Если одну нарезку сделать правой, а другую левой, то перемещение ползуна будет равно:

«-£( t + ti)·

При ί=<! скорость ползуна вдвое больше скорости поступательного движения винта.

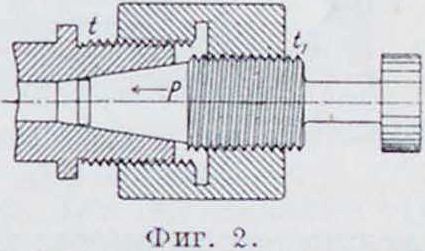
На том же принципе основана дифференциальная гайка, применяемая, между прочим, для закрепления фрезеров в шпинделе фрезерного станка (фигура 2). Обе нарезки делаются одного направления, и шаг !><,; отбрасывая влияние трения, получаем, что, при завинчивании гайки моментом М, сила, вжимающая конусный хвост фрезера в

Фигура 3.

отверстие шпинделя Ρ=ψ^, может быть сделана весьма значительной путем уменьшения разницы ходов нарезок гайки.

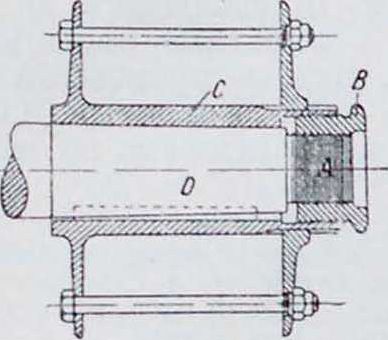
Другой пример дифференциальной гайки изображен на фигуре 3; гайка В, которая снабжена наружной и внутренней резьбами с различным шагом, навинчивается на винт А и одновременно ввинчивается во втулку С; перемещение втулки С относительно конуса I) за один оборот гайки I >авно разности ходов внутренней и внешней нарезок. Гайка показана в применении ко втулке воздушного винта авиац. двигателя АНЮ Ленинградской лаборатории двигателей; она позволяет не только натягивать втулку на конус при надевании винта, но также и стягивать ее при снятии последнего. Интересный пример Д. м. изображен на фигуре 4. Этот механизм служит для преобразования быстрого вращательного движения в медленное поступательное. Винты А и В приводятся во вращение от шестерни Е в различном направлении и со слегка отличающимися угловыми скоростями ω_ιи ω₂; червячное колесо G зацепляется одновременно с обоими винтами и вследствие разницы их угловых скоростей катится медленно по винту с более медленным вращением. Обозначая скорость вращения зубчатки Е через п (об/мин.), числа зубцов шестерен E. F и D—через ζ_χ, г_г и г₃, шаг винтов—через h (.и.и), получим скорость движения ползуна Н:

vh/г, ζΛ

^V=2"U - b) ^{ЛШ МПН}-

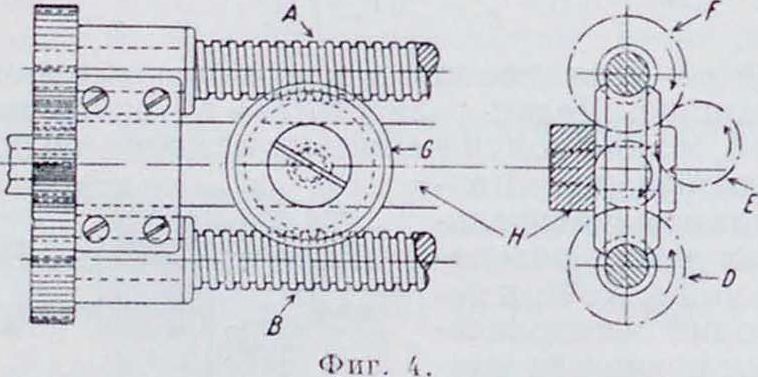
Насколько медленное движение можно получить посредством итого Д. м., видно из следующего примера: пусть п=100 об/мин., £j=20, л₂=100, z_z=101 и Ь= 3 м, тогда v=0,29~ миллиметров/мин.

Дифференциальный в о р о т. Канат в этих воротах (фигура 5) навернут в противоположных направлениях на барабан, имеющий два различных диаметра D и d. При вращении один конец каната сматывается, а другой наматывается на барабан. За один оборот блок перемещается вертикально на величину

h=*(D-d).

Называя скорость точки М через v, а угловую скорость вала через ω, найдем:

, D-d V — со

Пренебрегая трением, получаем подъемную силу ворота р ipL

D-d

При вращении вала блок .Vi движется не только вертикально, но также и в горизонтальном направлении в ту или другую сторону. Хотя за один оборот вала длина наматываемой и сматываемой веревки на диаметрах D и d различна, все же в горизонтальном направлении блок переместится только на расстояние одного витка, равное

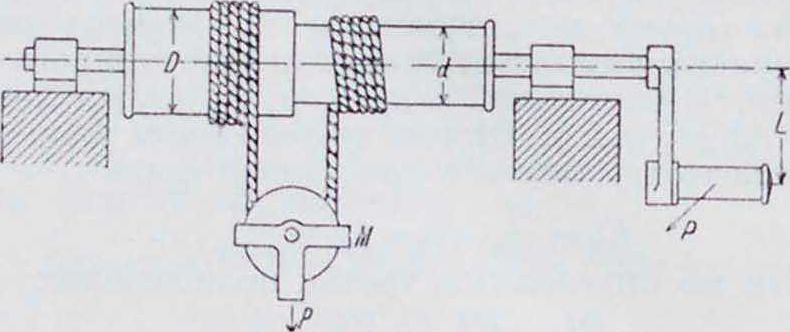
Фигура а. диаметру веревки, и благодаря этому ветви веревки, проходящей через блок, все время будут параллельны между собой.

Пит.: Зернов Д. С., Прикладная механика. Л. 1925; С т о л я р о в Я. Теория механизмов, Харьков, 1926; Д е л оме II., Лекции по практической механике, < ΓΙΒ, 1901. и. Бобарыков.