> Техника, страница 44 > Дифференциальные уравнения

Дифференциальные уравнения

Дифференциальные уравнения, соотношения, связывающие независимые переменные, искомые функции и их производные различных порядков.

Общий вид Д. у. η-го порядка:

F(x, у, у, у",.,»/(”))=0. (1)

Порядок высшей производной, входящей в ур-ие, называется порядком Д. у. Решить (интегрировать) Д. у. значит найти функцию у f(x), обладающую следующим свойством: если в ур-ие (1) подставить /(х) вместо у, f(x) вместо у, ., f х) вместо у⁽" то уравнение (1) обратится в тождество. Такая ф-ия называется р е ш сине м (интегралом) Д. у. Кривая, определяемая ур-ием у=/(х), называется интегральной кривой. Общее решение Д. у. есть решение, содержащее произвольные постоянные в числе, равном порядку ур-ия; т. о., для Д. у. η-го порядка общее решение имеет вид: y=f(x, С, С_г,., С„), где С_и С,., С„- -произвольные постоянные. Геометрически мы имеем семейство кривых, зависящее от п параметров. Всякое решение, которое получается из общего, если произвольным постоянным даны определенные численные значения, называется частным. Частное решение вполне определяется (то есть численные значения произвольных постоянных можно вычислить), если заданы началь-н ы е у с л о в и я. Эти условия для обыкновенного Д. у. таковы: ищется такое решение у, которое при данном численном значении независимого переменного х=х₀ принимает значение у₀, и его производные до (п—1)-го порядка, у, у",., у(^п ‘), принимают соответствен, значения у0, у₀, ···, у о ^,· П р и м е р. Д. у. движения тяжелого тела по вертикали: _uli=— 0, где (независимое переменное)—время, х (искомая ф-ия от <)—

высота тела в момент времени I, q—постоянное ускорение силы тяжести. Общее решение:

Y + C^ + C,.

Для определения С₁ и С., надо задать для начального момента t=0 высоту тела х₀ и

, dx

начальное значение производной _di, т.е.начальную скорость v₀. Для данных х₀ и v₀получим: х=— + v_ut + х₀. Решение Д. у.,

не получаемого из общего ни при каких значениях произвольных постоянных, называется особ и метров.

Методы интегрирования Д. у. 1-го порядка вида:

F(x, У, У)=0, (10

ИЛИ

?/)· (2)

Общее решение должно содержать одну произвольную постоянную.

Разделение и e р е м е н н ι»ι х. Предположим, что f(x, у) в ур-ии (2) есть произведение ф-пп только от х на ф-ию от одного у, т.е. f(x,y)· М(х) N(y). Пишем ур-ие при помощи дифференциалов dy— M(x)-N(y)-dx; разделяем переменные:

dy

mv>

М(х) dx.

Беря неопределенные интегралы от обеих частей, находим:

Sbfo-StiWta + C· (3)

Соотношение (3) дает возможность выразить у в ф-ии х и С, то есть дает общее решение.

II р и м е р: ~ — “. Разделяя перемен ные: у dy= —х dx, находим общее решение: х“ + ?/²=С.

Интегральные кривые образуют семейство концентрических кругов с центром в начале координат.

Однородное Д. у. 1-го порядка можно привести к виду:

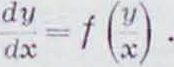
Для интегрирования вводим новую искомую функцию V при помощи соотношения:

⁴=и, или у - vx. Отсюда dy v dx + х dv.

Вставляя полученные выражения у и dy в данное Д. у., освобожденное от знаменателя dx, получим: v dx -f х dv=f(v) dx, или .t dv [/(г) — и] dx, или, наконец,

<1о _ dx

1(0)-о ~ X

Переменные будет:

разделены, и общее

S

dr

/(»)-»

In

х + С.

решение

Ii полученном результате надо еще замелить v через ^·

Липе и н о е Д. у. 1-го порядка. Так называется Д. у., в которое у и ^dJ_x входят в 1-й степени. Оно м. G. написано в виде:

^Г‘1 + Р-У Q, (4)

где 1’ и Q—ф-ни от х (или, в частности, по стоянные). Если в частности Q ^0, то имеем линейное дифференциалы!, уравнение вида:

dy

dx

Ру=о,

которое решается разделением переменных:

^{d и}=— Р ite; In?=-jp dx + С.

Взяв произвольное постоянное в виде С=In С, и потенцируя, получим окончательное выражение общего решения:

у=с, e~^Sr,lx.

Для интегрирования ур-ия вида (4), при Q тождественно не равном и, полагаем искомую ф-ию у равной произведению двухф-ий от х, наир., у=и v. Подставляя в ур-ие (4), имеем: u,v + u(v+P · v)=*Q. Подбираем функцию v так, чтобы выражение в скобках равнялось тождественно нулю: v + Pv 0, отку-

-fPdx, „ S Pdx

да г?=е ; тогда получим: и=Qc

и=Sq e^^Pdx dx т С и, наконец, общее решение:

у=е ^ ^Pcte[ С + SQc

И и т е г р и р у ю щ и и множитель. Всякое Д. у. 1-го порядка может быть представлено в виде:

М(х, у) dx + N(x, у) dy — 0. (δ)

Левая часть ур-ия (δ) будет полным дифференциалом, если существует такая функция и (ж, у), что ее полный дифференциал du - — М(х, у) dx + N(x, у) dy. Это значит, что ди _лт Ои ох

Оу а для выполнения этих ра венств, как доказывается в дифференциальном исчислении, необходимо и достаточно, чтобы имело место тождество: дм dN Оу ~ Ох

(6)

В этом случае ур-ие (δ) принимает вид: du=О,

и его интеграл будет и (х, у)=С. При выполнении условия (6) Д. у. (δ) интегрируется так: считаем у постоянным (dy --- 0) и интегрируем полученное равенство du=M(x,y)dx по х; получаем:

и --JM(x, у) dx + φ (у).

Мы написали ср(у) вместо постояв, интегрирования, т. к. она может зависеть от у, принятого за постоянное. Для определения <р(у) дифференцируем полученное равенство по ·?

ди _лт

и вследствие равенства ^ N получаем:

<p(y)=N-j dx,

откуда интегрированием по у найдем </?(?/), а следовательно, и и. Если условие (6) не выполнено, оказывается все яге возможным найти такую функцию μ(χ, у), по умножении на которую уравнения (δ) левая часть его становится полным дифференциалом. Такая функция называется и и т е г р и р у ю щ и м м и о яг и т е л е метров.

Пример. Д. у. у dx — (х + у) dy=0; левая часть его не является полным дифференциалом. Уравнение имеет интегрирующий

<р(у);

множитель ; умножив на него, получим: — — dy=0; М=‘, N--

у у“ ^J ’ у ’ у^г ’

дм _ dN _ 1

иу ~ дх у¹ ’

условие (6) выполнено. Имеем:

ди 1 Г dx, х х

dx у ’ ^J у ^{т ч}· у дифференцируем по у и приравниваем результат N:

-yi + ψ (»)— „ >

откуда <р(у)=-у·, <р(у)=- пу. Интеграл искомого уравнения есть и=* — In у + С.

Д. у. высших порядков. Д. у. 2-г о поря д-ка. Из Д. у. 2-го порядка только весьма немногие типы имеют решения, выражаемые с помощью знака неопределеного интеграла над данными функциями (знака, квадратуры). Рассмотрим иек-рые из этих типов. а) Д. у. не содержит у и ^ ; оно имеет вид:

8-м)·

Интегрируя 2 раза, получаем общее решение:

s-//(*) ^d* + c_i;

2/=J[ /(л) Йл] йх + С_гт + С

Сюда относится рассмотренное нами ур-ие:

d’x

w — e-

б) Д. у. не содержит у; оно имеет вид:

2-/(*£)·

Вводим вспомогательн. переменное р=^ ; уравнение будет 1-го порядка и примет вид:

•*1=/(“. Р)·

Если найдем его общее решение р=φ(χ₉0₁)₉то имеем:

dx “ °ι)>

откуда у=J* ιρ(χ, dx + С₂.

в) Д. у. не содержит х; оно имеет вид:

^d’^u=/i» ^,;ιΛ.

dx· y ’ dx)

Вводим новое переменное p и выражаем ^dd^d. следующим образом:

dy dx^1;

dp dx

iit i dy

dy dx

V ·

dp

dy

Получаем Д. у. 1-го порядка:

Проинтегрировав его, получим р=у>(у, С,), или ^=у(у, Ci). Разделяя переменные и интегрируя, получаем общее решение:

v(y, С.) ^{= ж} + ^С=·

Лине и н ы е Д. у. п-г о порядка вида: у^(п)+ р,у<“-«+. + р,.-!у + р„ у=/(ж), (7)

где Ρι,ρ₂, .,р„, вообще говоря, ф-ии от л; мы будем рассматривать, гл. обр., случай, когда все они—постоянные; тогда имеем ли нейное Д. у. с постоянными коэф-ф ициентами. Если /(л) 0, то Д. у. на зывается одно р о д н ы м (или без правой части), в противном случае неоднород-н ы м. Для линейного однородного Д. у. справедливы теоремы: если у, есть решение уравнения, то Су_х (С—постоянное) тоже— решение; если у, и у,—решения, то у_х + У тоже—решение. Поэтому для нахождения общего решения однороди. линейного Д. у. достаточно найти п частных решений (удовлетворяющих условию т. н. линейной независимости) у, у₂,., у„; тогда общее решение напишется так:

У ⁼ GiVi + С_а у₂ +. + С„ у_п. (8) Для неоднородного уравнения доказывается теорема: если известно частное решение Y неоднородного Д. у. и общее решение (8) соответствующего однородного ур-ия (то есть получаемого из уравнения (7) заменой /(л) нулем), то общее решение неодиородн. уравнения ость: у + Y. Переходим к уравнению однородному линейному с постоянными коэффициентами. Наша задача свелась к нахождению п частных решений. Ищем их в форме: у=е”’(геще неизвестное постоянное). Имеем: у=ге’^х, у" ------ rV^x,., y(n)·=rⁿe^rx.

Подставляя в левую часть уравнения (7) эти значения у, у",., у("),получим выражение: е^х (г“ + р₁ г’¹-¹ +. + р„- г + р„); приравнивая это выражение 0 и замечая, что е^^О, получаем для г алгебраическое ур-ие п-й степени (х а р а к т е ристичес к о е ур-ие): rⁿ + Piг^п~¹ + р_п-₁г + р_п=0. Это ур-ие имеет та корней; г, г, Если они раз личны, получаем п различных (линейно независимых) частных решений: е^г‘^х, е^г*“,., eV, и общее решение напишется в виде: у=С, е^г·* + С +. + С_п с’»*.

В случае, если какой-нибудь корень, пусть »!, имеет кратность больше 1, щапример 3, этому корню соответствуют три частных решения: е^г<^х, хе^г‘^х и хУ»“. Если в числе корней характеристич. уравнения есть мнимые сопряженные корни: α + βι на — βΐ, то им соответствуют частные решения у,=е^<а+,3,)х и y₂=e^(a-^il)x. Пользуясь формулой е^Лх=cos βχ + г sin βχ

и беря вместо у, и у₂ их линейные комбинации у_х=^!,’₂, у2=^1/1 “ ^! получим дна дей ствительных частных решения:

у_х=е"^ж cos βχ, у= e^JX sin βχ.

Π ρ и μ e p. y" + у + у=0. Характеристическое ур-ие: г²-(-г+1=0; его корни:

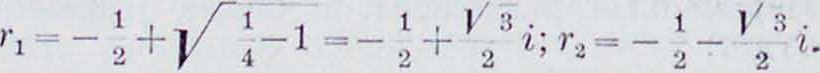
Частные решения:

	у2= с (- )·
или же:
- х х У з У i=e 2 cos ’,	у2=е 2 х sin * J
Общее решение:
— 1×Y у=е 2 cos	„. х |Ч 2 +C.S1H ’ )·

Чтобы получить решение неоднородного ли-

ценного Д. у., надо найти его частное решение. Если правая часть /(.т) имеет вид е“^хр(х), где р(х)—многочлен, то частное решение ищется в таком же виде: Y=c^ix-q(x), где q(x)—многочлен с неопределенными коэффициентами, которые подбираются так, чтобы Y удовлетворял неоднородному уравнению. Общее решение, как указано выше, будет у + Y, где у—решение однородного ур-ия.

Интегрирование с помощью рядов. Если решение Д. у. не выражается в элементарных ф-иях, можно искать его выражение в виде степеннбго ряда. Это метод особенно часто применяют к линейным Д. у. с переменными коэфф-тами для нахождения частных решений. Он состоит в следующем: ищем решение в форме степеннбго ряда

У=А₀ + ΑχΧ + А _гх² +. + А_пх^п + ·. (9)

с неопределенными коэфф-тами А₀, А, А₂₎. Подставляя в Д. у. вместо у ряд (9) и вместо у’, у"—ряды, получаемые формальным дифференцированием ряда (9), мы должны получить тождество; приравнивая нулю коэффициенты при разных степенях х, получим систему уравнений для определения А„, A_v Л_г., причем некоторые из этих коэффициентов могут остаться неопределенными,—они войдут в решение как произвольные постоянные.

Пример. Рассмотрим Д. у. Бесселя пулевого порядка: ху" + у + ху - 0. Подставляя в него вместо у и его производных ряд (9) и ряды, получаемые почленным дифференцированием, и собирая члены при одинаковых степениях х, получим тождество:

Л, + (1 · 2А, + 2А₂ + Л₀) х + (2 3Л, +

+ 3-4, + h,) х² +. + [та (И - 1) -4„ + пА„ +

+ Л„__г]х"-»+.=0.

Отсюда, приравнивая нулю коэфф-ты при различных степенях х, находим: А₂=0, Д_а =

- Ί; и вообще А_п=-^р Т. о.,

А₂=Л₅=. —А2„_ι=0;

А -^0__О

2“. 4* 2* · (ί · 2)· ’ * ’ *

4 (_ i »«

• · · ^уа2н V ^ι) 2^2η (1 · 2 .nj*

Л₀ осталось неопределенным; полагая А₀ 1, найдем частное решение уравнения Бесселя:

» V ₁ _ д-^:, х“ д ‘__,

У - 1 о< О “ ¹ 2·«. 1« + 2« · (1 · а)· 2* (1 · 2 - 3)· ^г · · ·

Это—функция Бесселя 1-го рода (смотрите 1 бессилены функции).

Система обыкновенных дифференциальных у равнений. Задача ставится так: найти я функций ?/, у_г,.,у_п независимого переменного ./·, удовлетворяющих п ур-иям, в которые входят независимые переменные, искомые ф-ии и их производные. Дифференцируя данные ур-пя несколько раз по х, мы получаем добавочные Д. у.; из полученной системы можно исключить все искомые функции, кроме одной, и свести, т. о., задачу к интегрированию одного Д. у. (высшего порядка).

Пример. Дана система двух дифференциальных уравнений:

2>-*Уг~У*= 0, ^ + 2^=0.

Дифференцируем 1-е уравнение по х:

<l*lh _ о Й/, _ dy_t „ dx* ° dx dx ⁵

заменяя 7 из 2-го ур-пя через -2у₁, полу чим:

•I’ll, _ « dy_{t 0}dx dx ^_1

Vi- 0

(линейное Д, у. 3-го порядка с постоянными коэфф-тами). Его общее решение:

У — (С_х + CsX) е^х+С₃е~^гх.

Из 1-го ур-ня находим:

//,=-з//₁+2.=”^2С>^βΧ-

— 2С., (х — 1) е^х + С₃ е~**.

Обратно, всякое Д. у. и-го порядка можно заменить системой Д. у. 1-го порядка введением новых функций. Пусть уравнение имеет вид (1); наряду с у вводим новые функции Ух=у, у-ι=у", ·., Уп-1=Тогда данное уравнение примет вид:

р (х,У.УиУг,···, Уп-1, 27) ⁼ °’ и к нему присоединятся еще η— 1 ур-нй:

^d’i ^d]l_=v

dx ^Jl’ dx ·’ y_x

Уп-1·

Общее решение системы п Д. у. 1-го порядка ^dax-fi(x,yu···, У_п), ···. 2In) (Ю)

зависит от п произвольных постоянных; оно имеет вид:

ΙΙι=<Ρφ>θ!,—,С„),.,у_п=<рф,С₁₉ .,C_n); (И)

для определения произвольных постоянных должен быть заданы начальные значения искомых ф-ий; при х=х₀ должны иметь: ?л=?/?,.

У,1=Уп (^гД^е Хо> У°1.Ун ^СУ^ТЬ заданные числа).

Систему решений (11) можно представить в другом виде, разрешая п ур-ий относительно п величин С_1г С_г, С₃,С„; получим: y>₁(x,yi,.,y„)=C₁,.,V„(x,y_l,.,y_n)=C_n. (12) Соотношения (12) называют интегра л а-м и системы (10).

Уравнения в полных д и ф ф e р е н-ц и а л а х с 3 переменными. Рассмотрим ур-ня вида

Р dx + Q dy + R dz=О,

где Р, Q, Λ—данные ф-ии от х, у, г. Если существует и нте г р и р у ю щ и и м и о ж н-т е л ь μ(χ, у, ζ), по умножении на который левая часть ур-ия становится полным дифференциалом’от некоторой функции м(х, у, ζ), то ур-ие примет вид dw= 0, интеграл его будет, очевидно, и(х, у, г)=С. Оказывается, не. всякое ур-ие имеет интегрирующий множитель; для его существования необходимо и достаточно тождествен, выполнение условия:

¹ [dz ϋ,ι) ‘ ^V (δχ dz) ^{1 11} [dy dz

Д. у. с частными производными. Так называется ур-ие, связывающее искомую ф-ию от нескольких независимых переменных, эти переменные и частные производные от искомой ф-ии. Д. у. с частными производными 1-го порядка с искомой ф-ней ζ и независимыми переменными х и у имеет вид:

^F (*· У> ^ζ> ί!χ ’ 2)=°·

Если производные

dz

Ox

dz

Ου

ВХОДЯТ В 1-11

п степени, миллиметров имеем линейное уравнение с частными производными. Оно имеет вид:

<¹³>

где Р, Q, R—заданные ф-ии от х, у, г. Его интегрируют следующим образом. Пишем систему (двух) обыкновенных Д. у.

dx dy __ dz I “ Q ⁼ ~R

(141

Как ранее указано (12), она имеет 2 интеграла: и(х, у, г)= С,; ν(τ, у, г)=С₂. Тогда общее решение ур-ия (13) примет вид: v-f (и), где /—произвольная ф-ин. Т. о., общее решение Д. у. с частными производными зависит от произвольной ф-ии. Для ее определения должен быть даны начальные условия (задача Коши): при х=х„, г должна обращаться в данную ф-ию <р(у). а именно z=<р(у).

П р и м е р. х + у Система (14) есть

dx rf|/__dz

х у ~ Z ’

ее интегралы: “=Ср “ -= С. Общее решение:

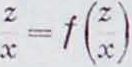
(/—произвольная функция).

Из Д. у. с частными производными 2-го порядка рассмотрим как пример ур-ие к о л с-б а и и я струны. Если t обозначает время, х—расстояние точки струны от одного конца (,г=0), х=I—второй конец струны, z—уклонение точки струны от положения равновесия, «—постоянную, то Д. у. напишется так:

Для нахождения определенного решения должен быть заданы: 1) граничные условия: г=0. при 1=0 и при х= I, для всякого ί; 2) начальные условия: мы должны при t =0 иметь:

z=/(л), ~-_х=/_L(.r) (где и Д—заданные ф-ии).

Ищем частное решение в виде z=XT, где×зависит только от х, Т—только от t. Подставляя это выражение для z в уравнение (15), находим:

Т" X" а^гТ ~ A

Так как левая часть зависит только от t, а правая—только от.г, то последнее равенство возможно лишь, если обе части равны одной и той же постоянной —/с²; получаем:

X" + Г-Х=0; T" + a² fc² Т=0.

Для 1-го уравнения имеем частные решения: Jil=cos fee;×= Sin lix. Используя граничные условия, имеем Х(0)=0, Х(1)=0; решение cos кх не подходит, а решение sin кх удовлетворяет условиям лишь при 0,

Отбрасывая нуль и отрица-

. 2п пп

i ··* ¹

тельные значения, получим численное множество решений для Т вида:

cos

nnat

i

, sin

final

l

и бесчисленное множество частных решений для z

ant. ηχ 2лη I. 2ηχ

COS, Sin, COS, Sill

I

l

l

l

nant. nnx COS sin.,

ant. nx. 2ant. 2nx

Sill ₍ Sin ₍, Sin ₍ Sin ₍ !

. nant.

. sin _{ sin

ηπ.X I ’ "

Решение данного Д. у. ищем в виде бесконечной суммы частных решений с постоянными коэфф-тами «„, 1)„:

и -- оо

ι χι ( final.,. nnat

z(x,t) 2j[ⁿ>t^C0S l + M^ln, J

nnx _/ir*_v

I sin .(1G)

Для определения постоянных «„, b_n воспользуемся начальными условиями; полагая в (16) I=0, получим:

71=00

1. ηηχ, V

2, ^sin i /(·»),

п=1

то есть а„ определятся как коэффициенты разложения данной ф-ии f(x) в тригонометрический ряд Фурье (смотрите Гармонический анализ). Далее, дифференцируя (16) по I и полагая t=0, имеем:

71=00

V ппа,. n.-rjc, _Ч

2j I ^»^sin i=/l(-«)> n=l

откуда b„ определятся через коэфф-ты разложения j.{x) в ряд Фурье.

Лит.: Фи длине Г. Дифферент!, ур-ия, пер. с англ., М. -Л. 1920; Гама р к и и И. Д. и С м и р н о в В. II., Курс высшей математики для техников и физиков, т. 2, Л., 1 926; С т е к л о в В. А. Основы теории интегрирования обыкновен. дифферент, ур-ий. М.- Л. 1927; Forsyth A. R. Lehrbuch d. Differential-gleichlingen, 2 Aufl., Brschw., 1 923. В. Степанов.