Диффракция

Диффракция. явления, наблюдаемые при огибании волнами встречных препятствий. Чаще всего при этом подразумевают нарушение прямолинейности распространения возбуждения и интерференционные процессы, сопровождающие огибание. Строго говори, Д. всегда сопутствует распространению воли (являясь, в сущности, синонимом этого распространения), но в непосредственно явной и отчетливой форме она обнаруживается для любых волн в том случае, когда размеры огибаемых препятствий соизмеримы с длиной волны или значительно меньшепоследней. Обычные звуковые, сейсмические и радиотелеграфные волны вполне удовлетворяют этому условию, и потому нарушение прямолинейности распространения и другие диффракционные явления здесь привычны. Большое значение—теоретическое и практическое—Д. имеет для оптики, ибо наличие диффракцион. явлений здесь—основной довод в пользу волновой теории света, главное средство для изучения свойств световых волн во всех частях спектра и одновременно — непреодолимое препятствие, ставящее предел разрешающей способности оптич. приборов (смотрите Оптические приборы. Микроскоп). Д. света легко наблюдать при рассматривании удаленного малого источника света сквозь очень узкие отверстия и сетки, при прохождении света около малых препятствий. Нек-рые метеорологии, явления (радуга, круги вокруг солнца и луны)— диффракционного происхождения. Д. объясняется и рассеяние света мутными средами. При наблюдении с белым светом в результате Д. и интерференции происходит разложение света в спектр, благодаря чему возникают различные хроматические картины.

Н моыохроматич. свете Д. обнаруживается чередующимися темньши и светлыми интерференционными полосами, кругами или пятнами. При некоторых условиях Д. сопровождается также поляризационными явлениями. Д. существует для волн любой длины, начиная от длинных электромагнитных волн и кончая жесткими у-лучами.

Характер диффракционных картин зависит от формы препятствий или отверстий, их размеров, способов наблюдения, состава падающего света и других условий. На вкладном листе (смотрите диффракциоиные картины 1 и 2, по фотографиям А. Г. Калашникова) виден результат прохождения параллельных видимых лучей через широкое отверстие в экране PQ и через очень узкое (тысячные доли миллиметров). Свет скользил по фотографической пластинке, поставленной J_ к экрану, и запечатлевал свой след на пластинке. Для широкого отверстии практически остаются в силе законы геометрия. оптики—образуется правильная геометрич.тень; для узкого отверстия эти законы резко нарушаются, свет через отверстие идет по всем Фигура i направлениям, но по нек-рым—преимущественно. Если бы отверстие было сужено до десятитысячных долей .и.и и далее, то распространение света стало бы равномерн. по полушару. Навкл.л.,3, видна сложная диффракционная картина при прохождении через клиновидную щель, контуры которой отмечены пунктиром. Нанкл.л.,4. приведена фотография диффракционной картины, подучающейся при прохождении света через малое круглое отверстие; на вкл.л.,5,—фотография тени конского волоса; навкл. л. 6,— фотография тени маленького диска. В отличие от 1 и 2, фотографии 3—о (по В. К. Аркадьеву) сделаны на большом расстоянии от огибаемого тела и с пластинкой, расположенной д к световому пучку.

Точная теория явлений Д. даже для самых простых случаев—одна из наиболее трудных, в математич. отношении, задач физической оптики. Существует несколько методой решения диффракдионных задач. Наиболее прост и нагляден метод Френеля; он основан па принципе Гюйгенса, дополненном принципом интерференции (смотрите). Трудность задачи в том, что волновая функция распределена по всему окружающему объёму, и первый способ ее упрощения состоит в том, чтобы свести объёмную функцию к функции, распределенной по поверхности. Это и достигается в элементарной прибли

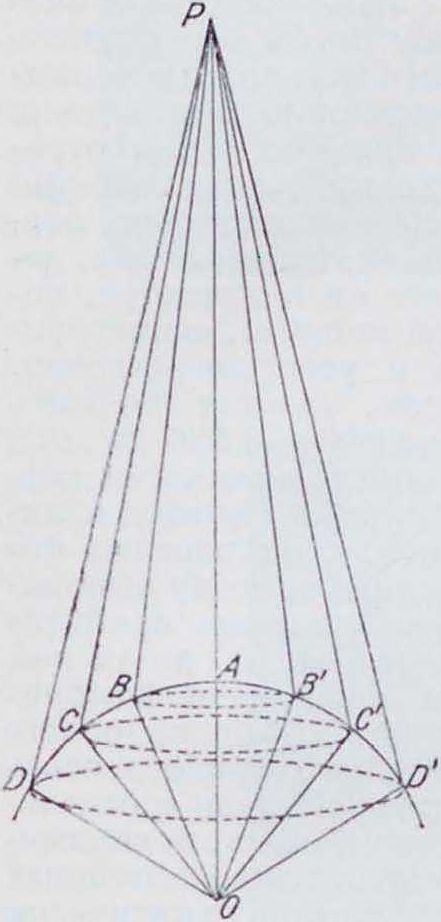
женной форме принципом Гюйгенса. Действие светящейся точки О на данную точку Р (фигура 1) заменяется действием поверхности волновой сферы ADD. Френель разбивает эту сферу на зоны (зоны Гюйгенса-Френеля) след, образом. Из точки Р радиусами

РА -f- I λ, РА + ² Я, РА + Ί Я,. проводят-ея сферы, рассекающие сферу ADD на шаровые зоны. Последующая зона, в среднем, имеет фазу волновой функции, противоположную предыдущей, и действие соседних зон (при отсутствии препятствий между О и Р) приблизительно нейтрализуется благодаря интерференции. Простой расчет показывает, что действие свободной, незакрытой волны на Р сводится к действию половины центральной зоны, что и соответствует в первом приближении прямолинейному распространению света. Если нек-рые зоны полностью или частью закрыты каким-либо экраном, то, меняя положение точки Р, будем получать в ней попеременно то усиление то ослабление света, что соответствует полосам, пятнам, кольцам. Метод Френеля неточен, он дает постоянную ошибку в фазе на £ (что не сказывается, впрочем, на интенсивности, единственно доступной опыту величине) и, кроме того, связан с другими упрощающими,произвольными предположениями относительно действия зон. Тем не менее для большинства простых диффракцион-ных задач этот метод вполне пригоден и дает хорошее совпадение с опытными данными.

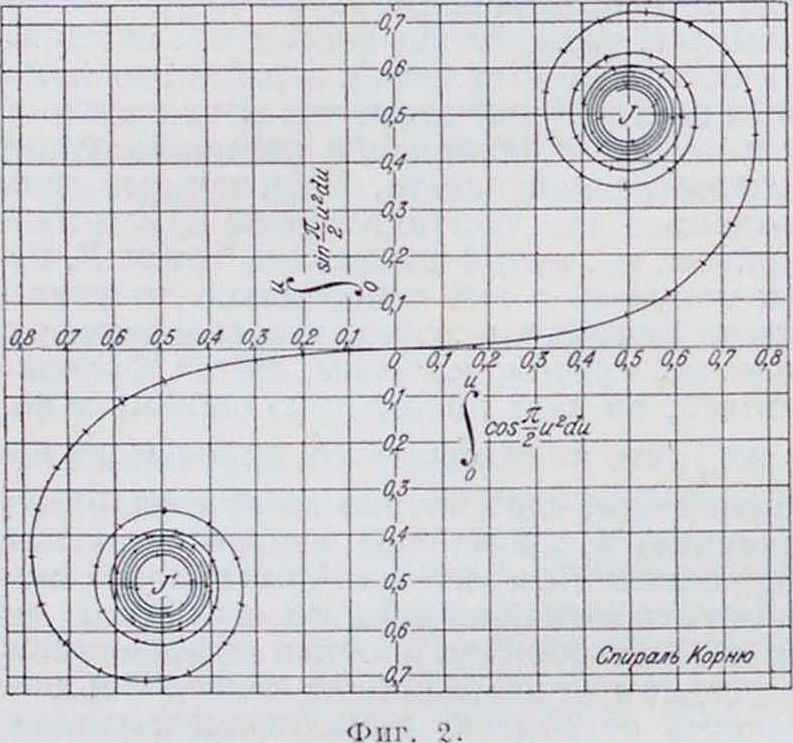
Различают два типа задач: 1) Д. сферич. волны (Д. Френеля) и 2) Д. плоской волны, наблюдаемой в параллельных лучах, например при помощи зрительной трубы, наведенной «на бесконечность» (Д. Фраунгофера). Решение задач первого типа значительно сложнее, чем второго. Окончательное выражение для интенсивности J в некоторой точке диффракционной картины имеет вид I =A-(C²+S²), где А—постоянная величина, а С и S выражаются через т. н. и н т е-г р а л ы Френеля:

и и

ξ= J cos " и- du; η= f sin * и- du.

У *0

Таблицы для этих интегралов имеются во всех подробных изложениях диффракцнон-пых явлений. Легко видеть, что

tfe’-f άη*=du-,

τ. е. и может считаться как элемент дуги некоторой кривой, отнесенной к осям f, η. Тангенс угла наклонения кривой к оси f, то есть

tg(0= tg Q м²),

τ. е. г“ радиус кривизны кривой

(>=Л- =, то есть обратно пропорционален длине дуги. Кривая асимптотически запинается вокруг точек (+ ², + J) и ‘).

то есть яв )яется спиралью (с п и р а л ь Корню, фигура 2). Спираль Корню служит весьма полезной геометрической интерпретацией интегралов Френеля, которая позволяет очень быстро представить общий характер диффракционной картины.

Более точный метод решения диффрак-ционных задач дан Кирхгофом. Объемную волновую функцию Ф, удовлетворяющую волновому ур-иго, Кирхгоф при помощи теоремы Грина сводит к функции на произвольной поверхности, охватывают, данную точку наблюдения. Значение волновой функции в этой точке, по Кирхгофу:

где интегрирование производится по всей указанной поверхности S, г—расстояние

некоторой точки поверхности от точки наблюдения, п—внешняя нормаль к поверхности; в подинтегральной функции, в Ф, время заменено через t—[, где с—скорость света. Приведенная формула и заменяет полностью принцип Гюйгенса-Френеля, являясь, в отличие от последнего, вполне точной. Однако, при практическом применении к диф-Фракционным задачам и этот метод не дает безукоризненно строгого решения; для этого требуется точное знание значений Ф и

(>Ф ,. „

-- на вспомогательной поверхности; в действительности же относительно этих функций приходится делать приближенные более или менее вероятные предположения, что удается довольно точно сделать в отношении коротких волн и трудно выполнимо для длинных.

Наконец, точное решение диффракцион-ных задач принципиально м. б. получено непосредственным интегрированием уравнений Максвелла приданных граничных условиях. Задачи такого рода весьма трудны и решены только для немногих простейших случаев. По мере усовершенствования теории получается’ все более тесное согласие теории и опытных данных, причем для лучей, дифф ротированных под большими углами но отношению к первоначальному направлению (Д. Гун), необходимо прибегать к точным методам. Современное развитие квантовой волновой механики (де-Бройль, Шредингер) позволяет надеяться, что клас-сическ. волновая теория диффракции света почти целиком (по крайней мере в отноше нии ее математического остова) может быть перенесена и в квантовую теорию света.

Д и ф фрак ц ионные р е ш е т к и. Явление Д. используется для разложения света в спектр в диффракционных решетках. Последние состоят из большого ряда щелей, расположенных на равных расстояниях и разделенных непрозрачными промежутками. В простейших диффракционных решетках щели получаются алмазной штриховкой плоского стекла посредством делительной машины. С таких решеток могут получаться целлюлондные реплики. Простую плоскую диффракциониую решетку можно также получить, фотографируя в значительно уменьшенном масштабе соответствующий чертеж. Диффракционные решетки для больших спектральных установок делают не для проходящего, а для отраженного света; штриховку наносят на сферических вогнутых поверхностях из зеркального металла. На таких решетках, достигающих 15 и более сантиметров в диаметре, посредством делительной машины, сконструированной Роуландом и усовершенствован. Майкельсоном и Вудом, удается наносить сотни тысяч штрихов (1 000—1 500 на миллиметров). При работе с вогнутыми отражающими диф-фракциониы.ми решетками становится излишним применение линз, сама решетка фокусирует спектры; благодаря этому возмозк-но изучение в вакууме спектров крайнего ультрафиолетового света от 100 до 10 m/t, который поглощается в кварце и флюорите (Милликен). Действие диффракционных решеток как спектрального прибора основано на Д. света от каждой щели в отдельности и на интерференции света, исходящего изо всех щелей. Теория диффракционных решеток для простейшего и практически важного случая Д. Фраунгофера (смотрите выше) может быть получена различными методами как на основании предположения о совершенной независимости монохроматических компонентов сложного света (ньютоновская смесь цветов), так и на основании учения о белом свете как некотором импульсе, который гармонически разлагается периодической диффракционной решеткой.

Теория приводит к такому выражению для интенсивности диффракционной картины в данной точке поля:

	2	ημύ
sin		sin
2		2
μη		sin /">
2		2

где ,Т_В—постоянная для данного случая величина; а—ширина щели; δ—постоянная диффракционной решетки, то есть расстояние между центрами двух последовательных щелей, /i=²^sin93, где φ — угол Д.; п — число щелей. Указанная функция представляет ряд чередующихся максимумов и минимумов. Основная группа тех и других, имеющая наибольшее значение при больших п, определяется равенством μδ-~.,

где к—ряд целых чисел. При к равном О или целому кратному от п получаются максимумы, в остальных случаях—минимумы.

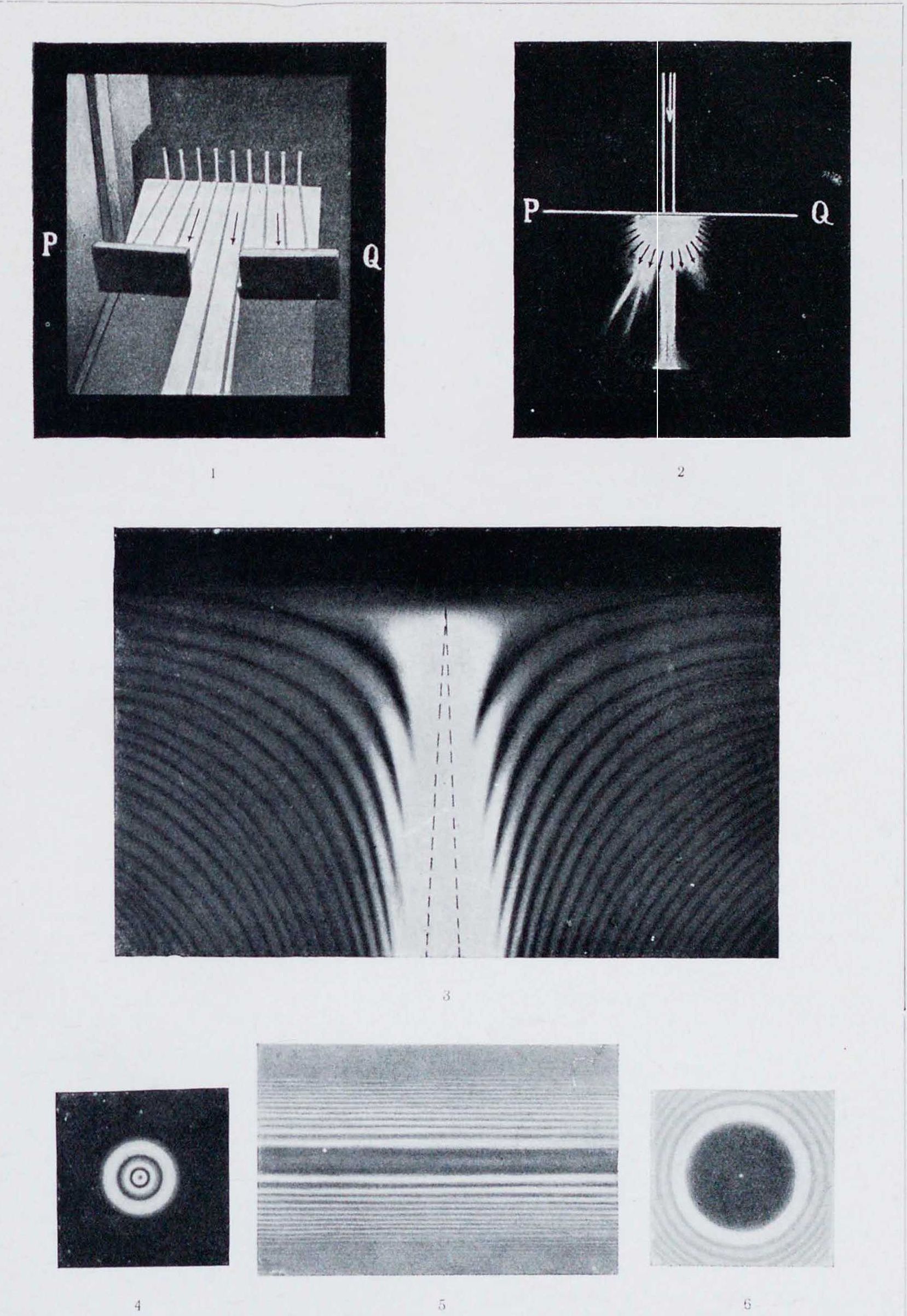
Диффракцмоннме картины: 1. При прохождении параллельных лучей через широкое отверстие. 2. То же через узкое отверстие. 3. При прохождении света через клиновидную щель. 4. То же через малое отверстие. 5. Тень конского волоса. 6. Тень маленькою диска.

Помимо указанных максимумов и минимумов имеются и другие, но значение их при большом п и надлежащем выборе отношения ^ь ничтожно. Обозначим: к=т-п, где т— 0,1,2 ., и введем значение μ в написанную формулу для максимумов; тогда она выразится в таком виде: sin<p_m=^. Для т 0 положение максимума не зависит от длины волны, получается неразложенное изображение коллиматорной щели (спектр нулевого порядка), для т=1, 2,. положение максимума зависит от λ, и свет разложится в спектры (спектры 1-го, 2-го и т. д. порядков) по обе стороны от спектра нулевого порядка. Из ф-лы sin φ =_ό для

Λ»λ легко видеть, что длина спектра 2-го порядка будет вдвое больше, чем 1-го и т. д. Отношение длин воли крайнего красного η крайнего фиолетового в видимом спектре приблизительно равно 2, поэтому спектры

2-го, 3-го и т. д. порядков будут все больше налагаться друг на друга, только спектр 1-го порядка останется чистым. Если, наоборот, λ > (1, то, как можно видеть из фор-тЛ

мулы sin φ=_ό, никакого спектра, помимо неразложенного спектра нулевого порядка, получиться не может. Поэтому кристалл, являющийся в сущности пространственной диффракционной решеткой, благодаря правильному расположению молекул не дает никакого диффракционного спектра при пропускании видимых лучей, но обнаруживает Д. для лучей Рентгена с короткой полной.

Характеристикой оптич. качеств диффрак-ционной решетки служит ее разрешающая способность. Таковой называется отношение длины волны λ к наименьшей разности длины волн M, двух соседних спектральных линий, которые еще воспринимаются как отдельные линии. Из уравнения диффракционной решетки следует, что т п, то есть разрешающая способность тем больше, чем выше порядок спектра т и число щелей п. Работа со спектрами высоких порядков затрудняется их слабостью и наложением спектров, поэтому повышение разрешающей способности делается главным обр. за счет увеличения п. С наиболее совершенными современными решетками „возможны измерения до тысячных долей А. Значительное повышение разрешающей способности м. б. достигнуто при почти скользящем падении лучей на решетку; этим воспользовался в последнее время Тибо для получения рентгеновских спектров от простой стеклянной решетки при отражении. Если придать углублениям штрихов на диффракционной решетке некоторый угол относительно плоскости решетки, то при известных условиях получается чрезвычайное усиление спектра какого-нибудь одного порядка; такой наклон получается применением резцов специальной формы. Диффракционные решетки такого типа (эшелетт Вуда) не получили, однако, распространения в силу практических трудностей. Спектры чрезвычайно высоких порядков используются в интерференционных спектроскопах.

Диффракционные решетки с различными штриховками (прямой, круговой) изредка применялись еще с 18 века для получения цветовой игры на пуговицах и других предметах. Вуд применил диффракционную решетку для цветной фотографии, по этот метод не получил распространения.

Лит.: Аркадьев В., Диффракщи Френеля, «Ж“, 1912, т. 44, фнзич. отд., выл. 4: Кал аш н и-н в А., Диффракмм Гуи-Зиммерфельда, <Ж>, 1912, г. 44, фиэнч. отд,. выл. 3; А н д р e е в Н., Электрич. колебания и их спектры, М., 1917; М og 1 1 ch К. Beugimg, Ilandbucli d. pliysikalischen Optik, hrsg. von Hebrcke. В. 1, p. 499, Lpz., 1927; В ouasse H. et Carrifire Z. Diffraction, P. 1923: Rleminn 0. F. imd Weber H., Die Differential- u. Integral-gleichungen der Meclianik und Physik, T. 2. p. 433, Braunschweig, 1927; M i c h e 1 s ο n A. A. Studies in Optics, Chicago, 1927. С. Вавилов.