Диффузия

Диффузия, происходящий во времени процесс выравнивания концентраций (парциальных давлений) в газе, жидкости или твердом теле, стремящийся к равновесному состоянию одинаковости концентраций. Такое определение Д. относится к системам, состоящим не менее, чем из двух компонентов, но и в однокомпонентном газе тоже может происходить Д., если под Д. понимать уравнивание давления во всех частях газа.

Д. изучалась с начала 19 в Дальтоном. Вертолле и Гремом, но только Фик в 1855 г. развил количественную теорию Д., показав, что кинетика Д. вполне аналогична кинетике теплопроводности (смотрите), теория которой была развита Фурье. Причиной Д. является наличие градиента концентрации с по направлению х, то есть Первый закон Фика для массы вещества elm, диффундирующей за время ch через поверхность 6, при условии, если градиент концентрации перпендикулярен к S, выразится таким образом:

dm=— DS * · άτ. (1)

Знак (—) указывает на то, что dm>0, если

_dx < 0, то есть если с надает с возрастанием х;

D—коэфф-т Д., измеряемый количеством вещества, диффундирующим за время άτ=1

через S=1 при градиенте ^=1; размерность

[ D I=^Гдл"^иа1-: в абсолютной системе единиц

^{L J} время ’

D измеряется в см- ск. Если принять, что D не зависит от с то из первого получается второй закон Фика:

дс дТ

д^гс

(2)

Физически это означает, что изменение с со временем в данном элементе объёма системы может происходить только в случае разли-

Ос —

чия градиентов _αχ с ооеих сторон этого эле-

дс мента, то есть только в случае, когда не равно нулю. Когда ^=Const, то^.=0 и по (2)^=0.

Наибольший интерес представляет Д. в газах и жидкостях. Д. в твердых телах происходит крайне медленно, хотя Робертс-Аустен интересными опытами и показал, что в прижатых друг к другу концами брусках металлов (например, Au и РЬ) происходит диффузия (спустя долгое время бруски резались на слои и анализировались).

Д.·—результат теплового молекулярного движения, и потому наличие процессов Д. является одним из доказательств молекулярного строения вещества. Здесь рассматривается Д. только свободная. О Д. через перегородки см. Диализ и Осмотическое давление. Математическая теория Д., сводящаяся, главным образом, к исследованию интеграла 2-го закона Фнка при различных предельных условиях, была развита в особенности Стефаном (1879 г.).

Д. газов и паров исследовалась двумя экспериментальными методами. Первый метод, кинетический, использованный в особенности Лошмитом и Обермайером, состоит и измерении парциального давления пли концентрации одного из компонентов в одном определенном слое диффузионного сосуда (д и ф ф у з и о м е т р а) с течением времени.

, Второй, стационарный, метод (Стефана) состоит в том, что в концах сосуда концентрации искусственно п одде рживаются все время постоянными: в нижней части поддерживается максимальная концентрация тяжелого компонента, например, соответствующая этому компоненту в чистом виде (Д., как всегда, производят против действия силы тяжести), а к верхней части с этого компонента поддерживается равной нулю. Тогда устанавливается стационарное, то есть независящее от времени, состояние Д., причем исследуется распределение с с высотой х (измеряется постоянный градиент ζ). Стационарный метод усо-

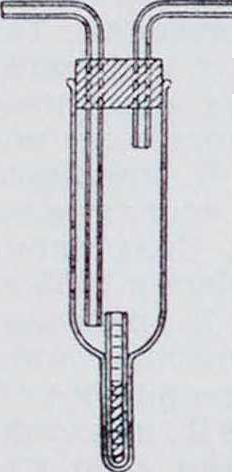
Фигура 1.

вершенствован Винкельманом и применен им к Д. паров. При этом пользуются, папр. прибором, изображенным на фигуре 1. Жидкость, находящаяся в капиллярной трубочке, поддерживает у своей поверхности давление насыщенного пара. Во внешней же трубке все время циркулирует какой-либо газ при атмосферном давлении, так что у конца капилляра парциальное давление пара жидкости равно 0, и жидкость испаряется только благодаря стационарной диффузии. Измеряя катетометром (смотрите) понижение уровня жидкости в капилляре, находят коэффициент диффузии пара в данный газ. Ниже в таблице приводятся некоторые значения В в см- ск.

Зиачен и я к о э <1* ф и ц и		м! т а	Д и Ф Ф У Ί I! И.
Диффундирующим пар		Д и (1) ф у з i		Я И
Диффундирующим пар	1	воз духе	со,	П,
С_еН,ОН (этиловый )	0° 40.4^е 66,9°	0.102 0,137 0.148	0,06» 0.090 0,103	0.378 0,503 0.543
С,н« (бензол)	i 0 „ и),9 : 15,0	0,075 0.088 0.101	0.053 0.061 0,072	0,294 0,341 0,399

Кривые распределения с с высотой х для разных моментов времени т (в общем случае) представлены на фигуре 2.

Молекулярво-кинетич. теория Д. в газах была разработана Клаузиусом, Максвеллом и другими и особенно Ланжевеном; простейшая теория дает для В выражение:

где λ—средняя длина свободного пути, ν— средняя скорость молекулярного (теплового) движения. Это выражение пригодно только

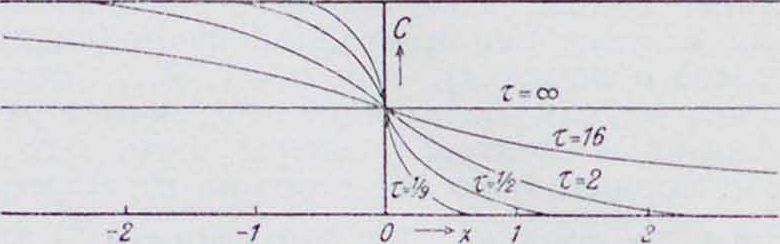
Фигура 2.

для малых е одного из компонентов или для Д. газа «в самого себя», и из него видно, что D должен быстро возрастать с (°, про-

порционально Т“; как видно из таблицы. /> действительно возрастает с темп-рой, причем D—kT". где п изменяется от 1,7 до 2,о. Для связи В с внутренним трением η газа молекулярно-кинстическ.теория дает: В

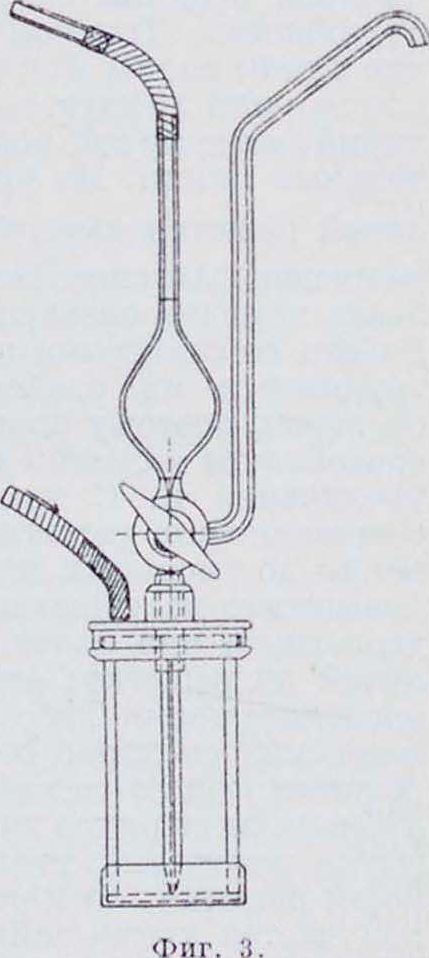
где у—плотность газа. При изменении парциального давления (или с) диффундирующего вещества В почти не изменяется. Д. в жидкостях подчиняется тем же законам и исследуется теми же методами, что и в газах. Так, Трем, Ёгольм и другие, а в особенности Сведберг, применяли кинотич. метод, выбирая из диффузиометра при помощи сифонной трубки последовательно 3—1 слоя одинакового объёма и анализируя их на содержание диффундирующего растворенного вещества. Па фигуре 3 представлен один из самых удобных диффузиометров — прибор Сведберга.

Заполнение пробной пипетки производится давлением воздуха, вдуваемого резиновой грушей или посредством газометра. Простейший метод измерения коэффициента В, без взятия проб, состоит в измерении коэффициента преломления для разных х или.

11ри стационарном методе, в измерении отклонения луча, проходящего через кюветку, где происходит Д., например в измерении смещения метки, видимой в микроскоп через кюветку (микроскопии, метод Фюрта). Для осуществления стационарности можно на дно сосуда помещать слой чисто го диффундирующего вещества. Заполненный водой сосуд помещают в большую банку с проточ

ной водой постоянной V (Фик). При этом все время с внизу сосуда будет наибольшей, а наверху с - 0; так как ^ - 0, то=Const,

то есть с будет линейно изменяться с х.

Законы Д. электролитов изучены Перистом, показавшим, что для случая полной диссоциации (в слабых растворах)

где и, V—подвижности катиона и аниона; иф V, и потому ионы разного знака диффундируют с разной скоростью, что создает всюду, где есть градиент концентрации, элек-трич. разность потенциалов—д и ф ф у з и о н-ный н от е и ц и а л, существующую пока вследствие Д. концентрации не выравняются. Д. электролитов разными методами ис- j следовал 15. С. Титов, показавший, меле- j ду прочим, применимость закона Фика и к смесям электролитов, если концентрации их рассчитывать в грамм-эквивалентах. D в жидкостях, как и в газах, значительно возрастает с <° и очень мало изменяется с с. Д. является чрезвычайно важным молекулярным свойством для суждения о величине растворенных частиц, то есть о коллондно-сти или кристаллоидности растворенного вещества (его степени дисперсности). К р и-с т а л л о и д ы. находясь в растворе в виде отдельных молекул или ионов, диффундируют быстро, Д. же коллоидов (смотрите) из-за большой величины их частиц—молекулярных сгустков (мицелл) сильно замедлена (в 100 и более раз) сравнительно с кристаллоидами. Рассматривая растворенные (наприм., коллоидные) частицы как шарики радиуса г. движущиеся в вязкой среде, и пользуясь для силы сопротивления среды движению каждого шарика выражением Стокса F-6 πτην (η—вязкость среды, V—установившаяся скорость движения, обусловленного наличием градиента осмотического давления dc

пт _d I, Эйнштейн и Смолуховский пришли к выражению:

I) обратно пропорционален г и η (закон Сведберга), и его измерение может служить для определения размеров частиц. D связан далее простым соотношением со средним квадратичн. перемещением х^г коллоидных частиц при броуновском движении (смотрите):

х²=2 · Ώ τ,

где т—время, для которого вычислено х^г.

В гелях, то есть в застывших, полутвердых коллоидных растворах (например, в желатине), Д. протекает практически с той лее скоростью, что и в чистом растворителе. Этим пользуются для устранения вредного влияния конвекционных токов при диффузионных измерениях. 1 ice обычные измерения Д. затруднительны из-за необходимости тщательно охранять прибор от сотрясений и от колебаний i° и потому производятся обычно в подвальных помещениях.

, Jum.: Т и м и р и з е в Λ. К., Кипетич. теории материи. 1923 (молен, кипетич. теория Д.

и газах); Titow W. S., <Ztschr. f. phys. Cliemie». Lpz. 1913. В. 84, ρ. 15; J e 1 1 i n e k К., Lehrb. d. phys. Cliemie. B. 2. p. 609 840, Stg., 1927 (общим обзор); Arndt К., llandbuch d. phys.-chem. Tcch-

nik, 2 Auflage, p. 602, Stg., 1923 (методика измерении); Stefan J., «Wlener-BeriQhte“. Wien, 1879, В. 2. j». 79. 161 (математическая теория); Со hen Е. mid Bruins II. It. Ztsehr. f. piiys. Cliemie», Leipzig. 1922, B. 103, p. 349. 1924, B. 113, p. 157 (обзор но-пых методов); Swedberg Т., Existenz d. Molekiilc, Leipzig, 1912. П. Ребиндер.