> Техника, страница 45 > Емкость

Емкость

Емкость электрическая между 2 проводниками—отношение заряда Q этих проводников к напряжению V между ними:

г, Q ° ⁼ V ·

Если Q измеряется в кулонах, а V—в вольтах, то С выражается в фарадах. Обычно пользуются более мелкими единицами емкости, микрофарадой (p.F) или нанофарадой (nF). Многие применяют в своих расчетах также электростатическую единицу емкости—с анти метр:

IF=10V-F=10⁹nF=9· 10¹¹ «см».

Различают Е. статическую и Е. динамическую.

Е. статическая. Статической называют Е., измеряемую в стационарном или квазиста-ционарном поле, когда можно говорить о разности потенциалов между проводниками. Е. статическая зависит от конфигурации проводников в электрич. поле и от промежуточной среды. Если один из двух проводников удален бесконечно далеко, то говорят о Е. уединенного проводника, равной заряду этого проводника, деленному на его потенциал, причем потенциал бесконечно удаленного проводника принимается равным нулю. Ниже приведены формулы для емкости

^/{~У ν,.ν. ’

уединенных проводников в среде с диэлектрическим коэффициентом ε.

1) Шар радиуса г (см):

С=ε 1,11 10^_6 · r yF, т. о., Е. земного шара

С=1,11 · 10-° 6,37 · 10⁸=710 yF.

2) Эллипсоид вращениясполуосямиа>Ь=с:

2,22 · 10-⁶ · yF (е²=рР)

С-

In

3) Эллипсоид вращениясполуосями&<а=с: С=1,11 · 10^-£

yF(e

arc sme

4) Тонкая шайба радиуса г:

С=0,71 · 10"« -ε-г [J.F.

Если оба проводника расположены на конечном расстоянии друг от друга, причем большинство силовых линий, исходящих от проводника с большим потенциалом, попадает на второй проводник, то они образуют конденсатор (смотрите).

Приведем ф-лы для Е. различных конденсаторов в среде с диэлектрич. коэфф-том ε:

1) Две круглые шайбы, толщина которых d, а радиус"?, на расстоянии а:

С=0,884 · 10~⁷ · ε · Г— + г fin ¹⁶^ +

₊ l₊^.ln^)],F.

Если а « г, то

С=0,884 · ΙΟ-⁷ ·,ε р yF.

2) Две концентрические сферы с радиусами г и R:

С=1,11 10-« · ε · —yF.

¹ " R

3) Цилиндрический конденсатор, радиусы внешней и внутренней обкладок которого г и R, а длина I:

С=5,55 · 10~⁷ · ε · -^ yF.

In — r

4) Два эксцентрич. цилиндра радиусов г_хи г₂, длиной I при расстоянии осей d.

а) Один цилиндр внутри другого:

С=5,55 · 10“⁷ · ε------yF,

^1η2^^{(?1 + ,1+?ί)}

fc²=(r| + rf)² — 2d² (r² + rl) — d^l. б) Один цилиндр вне другого:

С =5,55 · 10-⁷ · ε----ί-[j.F,

^ln2^^[d‘^{_(r! + ri) + &]} fc²=d¹ - 2d² (r² + r²) + (r - r²)².

5) Цилиндр радиуса r и длиной l, параллельной бесконечной плоскости на расстоянии d от оси цилиндра:

С=5,55 ΙΟ"⁷ · ε · - --- (iF.

Аг sh -

г

6) Провод радиуса г см, подвешенный на расстоянии h сантиметров от земли:

С=5,55 · 10^-2 · yF/км (h »г).

in —

Г

(См. также Емкость антенны.)

Несколько проводников. Если электрич. поле ограничено больше, чем двумя проводниками, то понятие Е. усложняется, т. к. заряд каждого проводника в этом случае зависит от потенциала других проводников. Если имеется система из п проводников и земли, потенциал которой принимают равным нулю, то заряды q_{ и потенциалы u_t(относительно земли) этих проводников связаны между собой линейными ур-иями:

П

^ui ⁼ 2 ^аи⁽1>. ⁼ 1>2,3,. ,п).

;.=ι

Коэфф-ты а_а называются потенциальными коэффициентами. Они симметричны, т. e. а_и=a_;i. Коэфф. a_a равен потенциалу, к-рый устанавливается на проводнике г, когда проводник А получает заряд q_!i=1, а все остальные проводники не имеют зарядов. Решая данную систему ур-ий относительно зарядов q_it получают систему линейных ур-ий:

П

Яг ⁼ 2 βιλ^λ ⁼ 1>2,3,···? УЬ)· λ=ί

Коэфф-ты Ргх. пропорциональные минорам определителя (a_i;), тоже симметричны, то есть Д_а=/З_л{,и всегда>0. Коэффициенты^ называются коэффициентами электрической индукции. Обыкновенно пишут:

β«=Сд + С_1г +. + C_in,

и, т. о., получается след, система уравнений: Д=СцЩ-)- С₁₂(и_х— щ) +.+ Οχ_η(Μι—и_н), q%⁼⁼ 0₂x(w₂ «i) “г К ··· К С_2г,(?ц >

Цп^ E_ni(u_n и_х) -J- С_п2(и_п u₂) H-. C_nnu_n.

Коэфф-ты C_a называют E. проводника г относительно земли, а —частичной Е. меж ду проводниками г и А.

Рассмотрим несколько таких систем.

1) Два провода с радиусами г_х и г_г подвешены на высоте h_xи h₂ на расстоянии d₎₂друг от друга (фигура 1).

Для решения этой задачи рассматривают зеркальные изображения 1 и 2 проводов 1 и 2 относительно земли и расстояние h₁₂, между 1 и 2. Тогда 2ίι,

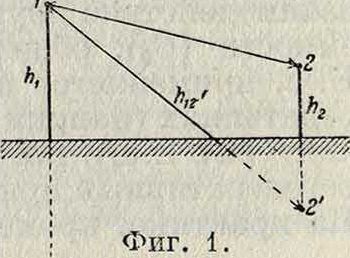
Οχ= 5,55 · 10-²

In -

D

[xF/км,

In

Со=5,55 · ΙΟ²

2 h,

(aF /KM,

ln

- C₁₂=5,55 · 10-² · -p yF/KM,

где

D

Если r₁=r₂=r, fe₁=/i₂=fe, то

С_г= C₂=5,55· ΙΟ^-2·

- C_I2= 5,55-10-

, 2 ft In —

Г

Ы’£_Г-Ы^Щ

V d² + ih‘

μ-F/KM,

In-

КИ

*£*£*!)

Аналогичные ф-лы выведены для трех- и четырехпроводных линий, для многожильных кабелей, для электронных ламп. При расчете Е. системы цилиндрич. проводников пользуются по б. ч. методом изображений электрических (смотрите) и методом конформных отображений (смотрите Электростатика). Следует отметить, что Е. между двумя проводниками обратно пропорциональна электрич. сопротивлению между этими проводами, так что задачи расчета Е. и расчета сопротивлений математически эквиваленты.

В том случае, когда проводники соединены т. о., что все силовые линии проходят последовательно от одного проводника к следующему, эти проводники образуют цепь последовательно соединенных конденсаторов, имеющих один и тот же заряд Q, причем напряжение щ на обкладках каждого конденсатора обратно пропорционально его емкости Ср.

Q

^ui - а ‘

Общая емкость С всей системы определяется по формуле:

i₌yl ₌ i ₊ i₊.₊l.

С Ci С, ^τ С* ^{1 т} Сп

При параллельном соединении, когда напряжение и на обкладках всех конденсаторов одинаково, заряд Q_{ распределяется пропорционально емкости С,_: этих конденсаторов:

Qi^CiU,

а общая емкость С всей системы определяется по формуле:

с-·2 σ,-σχ + σ, +. + c».

См. Конденсаторы электрические.

Е. динамическая. При быстрых колебаниях не существует электрич. потенциала.

В этом случае напряжение между двумя точками зависит от пути, по к-рому измеряется это напряжение. Можно условиться называть динамич. напряжением и_дт плоского конденсатора линейный интеграл напряженности электрич. поля вдоль пунктирной линии ABGD (фигура 2). Тогда динамич. Е. С_д. определится как отношение заряда конденсатора q к его напряжению и_д:

С_д =-?- ·

°· щ.

Величина С_д. зависит и от среды и от частоты тока, так что при быстрых колебаниях поле распределяется неравномерно внутри конденсатора.

Статическая E. С отличается от С_д., и отношение ™=a_v называется множите

В А		,с ID

Фпг. 2.

лем вытеснения (Verdrangungsfaktor). Этот множитель в случае круглого плоского конденсатора радиуса R, при расстоянии d между обкладками и круговой частоте со:

(Н

где а²

9 · 10²⁰

(%

СИ

диэлектрич. коэффициент

-R

а вакуума, ε—диэлектрич. коэфф-т данной среды, вообще говоря, комплексный и только для совершенных диэлектриков являющийся действительным числом). Функции 1_г и 1₀—бесселевы ф-ии первого и нулевого порядка. При критических значениях частоты ф-ии 1_г или 1₀ обращаются в нуль, и, соответственно, динамич. Е. становится равной нулю или бесконечности. Эти частоты соответствуют частотам собственных колебаний конденсатора. Практически такое изменение Е. может возникнуть только при очень больших частотах. Так, например, конденсатор, у которого R=10cm, ε= ε₀, т. e. α=3·10¹⁰ см/ск, будет иметь первую критич. частоту при ω=7,2·10⁹, то есть при 10^s пер/ск.

В начале развития электротехники пользовались низкими напряжениями, при которых Е. не имела большого значения (Лейденская банка). В наст, время при громадном росте применяемых напряжений значение электрич. поля, а следовательно, и Е. в технике сильных токов все увеличивается (кабели, воздушные линии, защита). Еще более существенной является роль емкости в технике связи, при определении частоты колебаний и связи между собой электрических цепей.

Лит.: Круг К. А., Основы электротехники, М., 1926; Maxwell С. J., Treatise on Electricity а. Magnetism, L., 1882; О r 1 i c h E., Kapazitat und In-(iuktivitat, Brschw., 1909; С о ti e n L., Formulae a. Tables for the Calculation of Alternating Current Problems, N. Y., 1913; Breisigf., Theoretische Tele-graphie, 2 Aufl., Brschw. 1924; Ollendorff F., Die Grundlagen d. Hochfrectuenztechnik, Berlin, 1926; Wagner K. W., «Archiv fiir EleMrotechnik», B., 1920. B. 8, p. 145. Я. Шпильрейн.