 > Техника, страница 46 > Железобетонные конструкции
> Техника, страница 46 > Железобетонные конструкции
Железобетонные конструкции
Железобетонные конструкции,
конструкции, материалом которых служит железобетон (смотрите).
I. Основные элементы Ж. к. и их сочетание.
Проектирование Ж. к. сводится к целесообразному комбинированию основных элементов, работающих: на изгиб (плиты, балки), на центральное сжатие столбы, колонны), на внецентренное сжатие (своды, арки, рамы).
I. Плиты. Простейшую Ж. к., работающую на изгиб, представляет собою плита прямоугольного поперечного сечения. Признаком плиты является незначительная ее высота по сравнению с поперечными размерами. Если отношение сторон плиты в плане меньше 3 : 2, то она рассматривается как пластинка, опирающаяся по всему контуру (четырехсторонние плиты).Плиты, имеющие отношение сторон, равное или большее 3:2, рассматриваются как балки (балочные плиты), подверженные простому поперечному изгибу на пролете, равном меньшему из ее двух измерений. Расчет и конструктивное выполнение железобетонных плит обусловливается способом их закрепления на опорах. В этом отношении плиты подразделяются на: а) свободно лежащие, перекрывающие один пролет и опирающиеся свободно, без всякой заделки в опорах; б) заделанные, то есть такие, которые жестко связаны с опорами путем заделки их в стену или забетонирования, причем между заделанными плитами различают: аа) совершенно заделанные, если заделка так велика, что при различных загрузках исключается поворот опорного сечения и бб) частично заделанные, если закрепление в опоре не воспринимает полностью момента и возможен ограниченный поворот сечения; в) кроме того, можно различать консольные плиты, имеющие только одну опору с полной заделкой защемленного конца или вынесенные за опору по продолжению плит, перекрывающих пролеты; г) неразрезные, перекрывающие несколько пролетов и находящиеся во взаимной жесткой связи; опорами таких плит м. б. стены и балки; концевые опоры таких многопролетных плит м. б. также свободными, частично или полностью защемленными. Плиты между железными балками м. б. выполнены как свободно лежащими в пределах одного пролета, так и неразрезными. В продольном разрезе плита имеет прямоугольное сечение. Неразрезные и упруго (частично) заделанные плиты снабжаются иногда у опор утолщениями, или т. н. в у-т а м и, необходимость которых вызывается отрицательными опорными моментами, превосходящими по величине наибольшие положительные моменты. В консольных плитах изгибающие моменты убывают от плоскости заделки к свободному концу, чем и обусловливается конструкция такой плиты.
Арматура в плитах разделяется на рабочую и распределительную. Основная рабочая арматура в плитах вытянута, но встречается также и устройство арматуры в сжатой зоне. Расстояние от крайнего сжатого волокна до оси вытянутой ар-
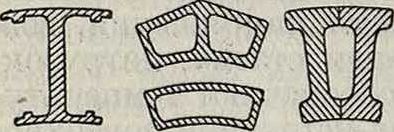
Фигура 2.
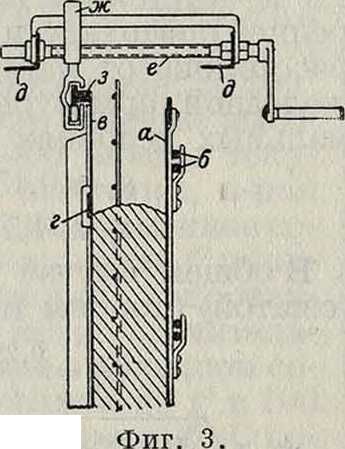
Плиты
Эскизы плиты и арматуры
Возникающие напряжения
Расположение арматуры я
Θ
й о
«
СО
S
Θ
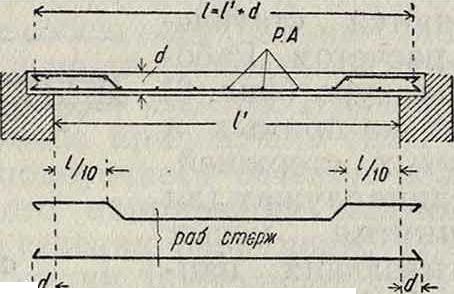
РА роспред арматура
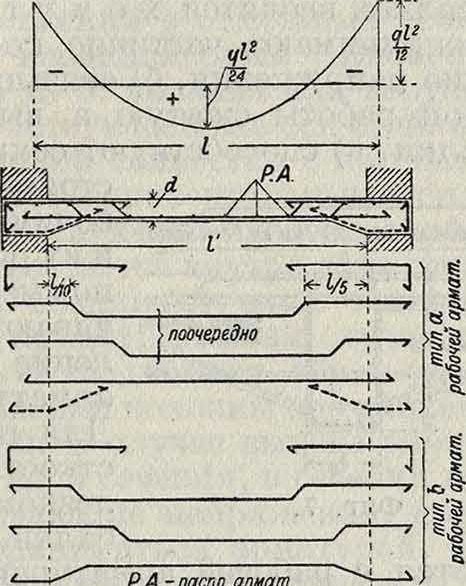
Р.А.-распр. армат.
Только положительные моменты растяжения на нижней стороне плиты; косые растягивающие напряжения
Арматура укладывается, в соответствии с изгибающим моментом, внизу плиты; косые растягивающие напряжения воспринимаются отгибом вверх части стержней арматуры у опор
Отрицательные моменты на опорах; положительные моменты в пролетах
Арматура располагается соответственно знакам моментов: внизу—в области положительных и вверху—в области отрицательных моментов; количество той и другой арматуры должно соответствовать абсолютным величинам моментов м л в о о
Я
о й
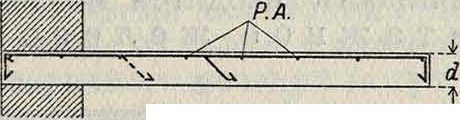
Растянутая зона наверху
Арматура располагается наверху плиты
Р.А.-распр. армат
Р.А.
UAr-
Р.А.
Не
| τ | ! | |
| LL’A - | поочередно, | |
| f VA | j ; |
положительные моменты в пролетах, отри цательны е—на промежу точных опорах
Арматура располагается соответственно знакам моментов: внизу—в области положительных и вверху—в области отрицательных моментов; количество той и другой арматуры должно соответствовать абсолютным величинам моментов возможны сквозные стержни при одинаков, диан. и располож. матуры называется рабочей толщиной плиты. Расположение рабочей арматуры в плитах зависит от знака изгибающих моментов.
Плиты с двойной арматуро й— растянутой и сжатой—применяются в тех случаях, когда стеснена конструктивная высота; в многопролетных плитах необходимость двойной арматуры может вызываться переменностью знака момента при различных положениях временной нагрузки.
Распределительная арматура предназначается для связывания стержней рабочей арматуры в поперечном направлении с целью обеспечения неизменяемости расстояния и равномерного распределения усилий между ними, а также для противодействия образованию трещин от усадки и температурных колебаний; она также необходима в виду наличия опирания по контуру, к-рое влияет на распределение напряжений даже и при удлиненных контурах. В местах пересечения распределительная арматура связывается с рабочими стержнями отожженной проволокой. Количество распределительной арматуры должно составлять ок. 15% рабочей. В плитах, опертых по всему контуру, арматура располагается по двум взаимно перпендикулярным направлениям, причем обе системы являются рабочими.
2. Балки. Балки представляют собою конструкции, несущие расположенные на них перекрытия, кровли и тому подобное. и работающие на изгиб и на срезывание. В конструктивном отношении различают балки: а) прямоугольные (фигура 5), отличающиеся от
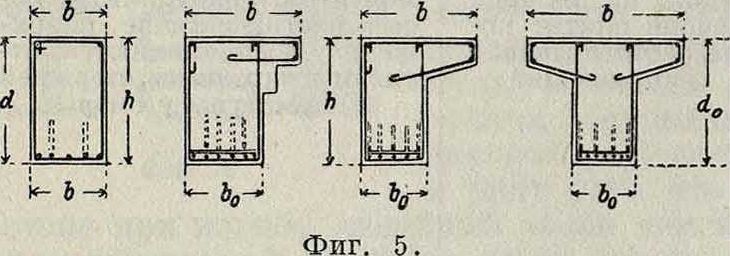
плиты своей сравнительно небольшой шириной и б) тавровые, или плитобал-ки (фигура 6), в которых плита играет роль сжатого пояса.
В отношении способа закрепления на опорах балки, подобно плитам, разделяются на свободно лежащие, заделанные, консольные и неразрезные, причем признаки этих видов заделки остаются для балок те же, что и для плит. В то время как в плитах, вследствие их большой ширины, скалывающие напряжения имеют вообще малое значение по сравнению с напряжениями от изгиба, в балках, вследствие их ограниченной ширины, скалывающие напряжения играют весьма существенную роль и должны всегда строго учитываться.
Балки располагаются: в одном направлении или по двум взаимно перпендикулярным направлениям, образуя в последнем случае кам, которые опираются на стены или стойки (столбы, колонны).
Арматура балок состоит из рабочих стержней, хомутов и монтажного железа. Число и диаметр рабочих стержней оп-р еделяются статическим расчетом. Рабочая арматура (фигура 8) состоит из прямых и отогнутых стержней.
Последние служат для воспринятия косых растягивающих напряжений. Как в обыкновенных (прямоугольных), так и в тавровых балках вводятся хомуты, которые: а) воспринимают частично косые растягивающие напряжения, б) связывают для совместной работы сжатую и вытянутую зоны балки, в) способствуют сохранению расстояния между рабочими стержнями и их расположению по высоте, г) увеличивают сопротивление скольжению арматуры в бетоне. Для придания жесткости всему железному каркасу балки, хомуты связываются с рабочей арматурой, а для сохранения расстояния между ними и для устойчивости вводится монтажное железо. Монтажное железо служит для:
ь
| i 4 X | ||
| н
io | ||
Фигура 6.
ίαβ. стерж. 8 07мм на 7 пог. метр
| 1 - | 1распр. армат. | |
| арн^плиты &о | плиты | |
| - | ||
Фигура 7.
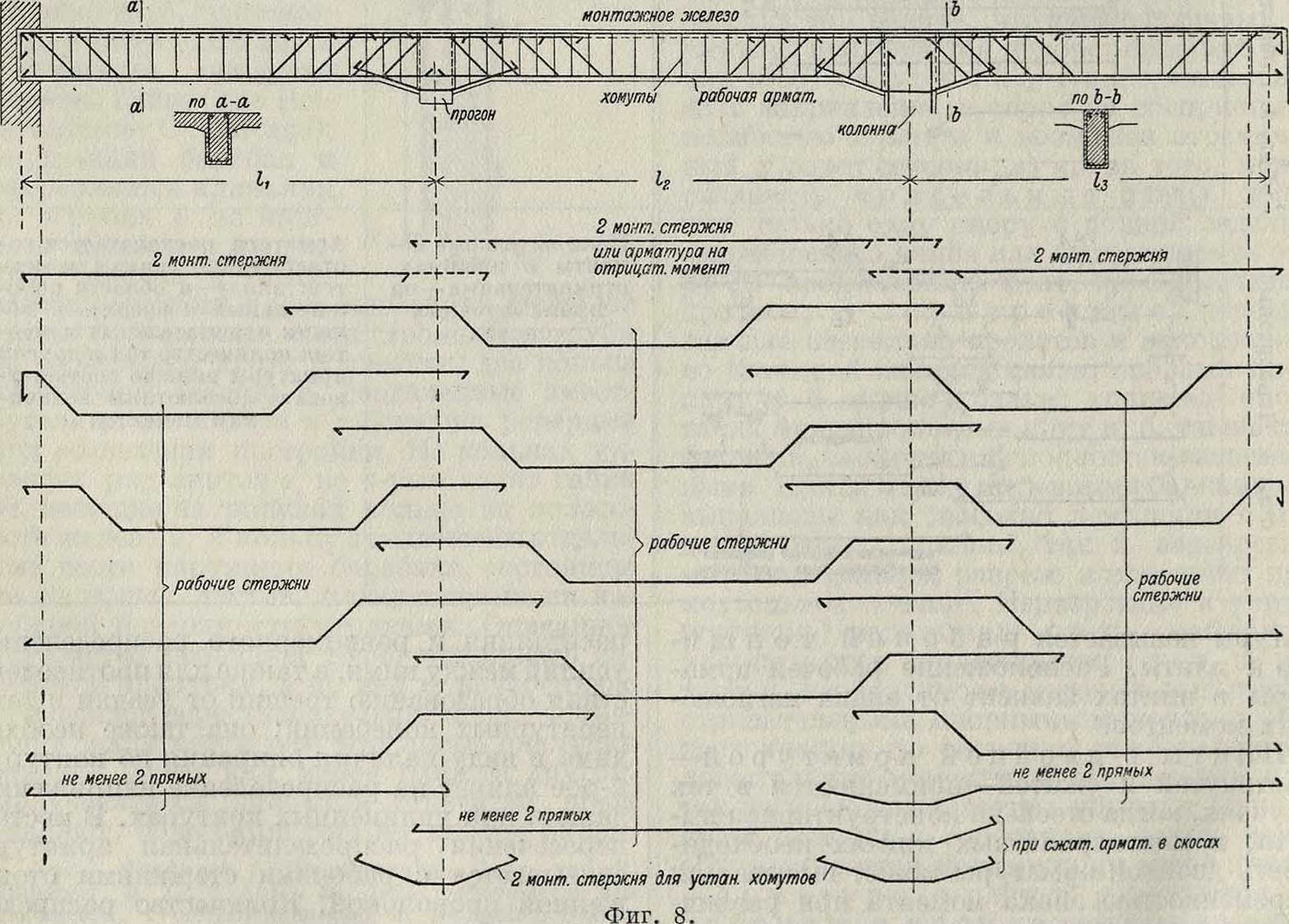
балочные клетки. Балки одного направления (фигура 7) считаются главными (прогоны), а другого — вспомогательными. Последние передают нагрузку от плиты главным бал а) поддержки хомутов, б) целесообразного выполнения сборки арматуры, в) удержания в балках на должной высоте отогнутых стержней плиты, а в прогонах—добавочных стержней, служащих для связи с плитой,
г) предохранения конструкции от образования трещин вследствие усадки бетона, температурных колебаний и других воздействий.
3. Колонны. Столбы и колонны представляют собою вертикальные элементы конструкции и могут работать на центральное и внецентренное сжатие. При центральном сжатии точка приложения силы совпадает с ц. т. поперечного сечения колонны, вследствие чего напряжения сжатия распределены по сечению равномерно. При вне-центренном сжатии продольная сила, сжимающая стойку, не проходит через ц. т. отдельных сечений, вследствие чего распределение напряжений в отдельных сечениях оказывается неравномерным. Внецентрен-ная нагрузка м. б. вызвана или вертикальной силой, действующей вне оси стойки, или продольной силой совместно с изгибающим моментом или с горизонтальными силами. Если равнодействующая внецентренно приложенных сил остается внутри ядра сечения, то в сечении возникают одни сжимающие напряжения; арматура в этом случае также сжата, и роль ее сводится гл. обр. к увеличению сопротивления колонны по сравнению с чисто бетонной. В случае выхода равнодействующей из ядра сечения, в сечении возникают растягивающие напряжения, которые должны восприниматься арматурой. Высокие тонкие колонны во избежание опасности от продольного изгиба делают всегда железобетонными, в то время как стойки с незна-чительн. отношением их высот к наименьшему размеру поперечного сечения могут иногда выполняться из бетона без арматуры.
По характеру выполнения стойки подразделяются на свободно стоящие, устойчивость которых достигается заделкой их в фундамент, истой к и с заделкой или шарнирным закреплением как вверху, так и внизу. Стойки опираются на фундамент, причем если последний сделан из материала, допускающего меньшее напряжение, чем принято для стойки, то давление последней на фундамент передается посредством башмака (развитие сечения в подошве стойки), или т. н. базы. При одинаковых допускаемых напряжениях как в стойке, так и в фундаменте надобность в башмаках отпадает. При несимметрично нагруженных стойках фундаменты под них проектируются в соответствии с действующими на них силами. В соответствующих случаях требуется надлежащ, заделка стойки или ее башмака в фундамент. При действии сил с двух сторон учитывается при расчете фундаментов наименее выгодная односторонняя нагрузка для каждого направления. Для получения возможно равномерного распределения напряжений в основании рекомендуется устраивать в соответствующих случаях несимметричные фундаменты в соответствии с воспринимаемыми ими усилиями. Сечение стоек бывает квадратное (фигура 9), прямоугольное, многогранное и круглое.
Арматура разделяется на продольную и поперечную. Продольная арматура состоит из прутьев (обыкновенно круглого сечения), расположенных вблизи наружной поверх ности стойки. Поперечной арматурой служат хомуты (также из круглого железа), которые связывают продольные стержни, усиливают их сопротивляемость продольному изгибу и воспринимают напряжения от поперечного расширения бетона при действии продольной силы. Взамен хомутов м. б. применена кольцевая или спиральная арматура. Под колоннами с кольцевой (фигура 10) или спиральной (фигура 11) арматурой (бетон в обойме) подразумевают только стойки с круглым ядровым сечением. При определении размеров столбов или колонн с кольцевой или спиральной
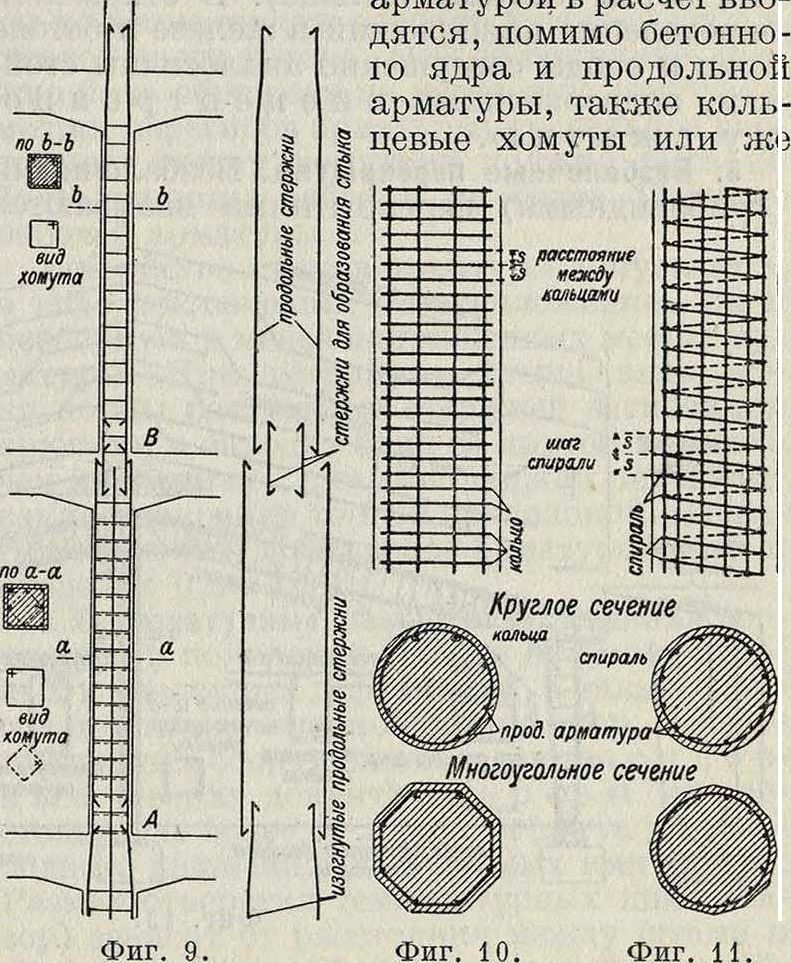
спираль, охватывающие внутреннюю часть сечения. Иногда применяются колонны с ядром из чугунной трубы, заключенной в бетон в обойме.
4. Арки и своды. Аркой (фигура 12) называют кривой брус с таким устройством опор, при к-ром под действием вертикальных сил возникают наклонные опорные реакции. Если измерение арки в направлении, перпендикулярном к ее плоскости, велико по сравнению с друг, размерами, то она называется
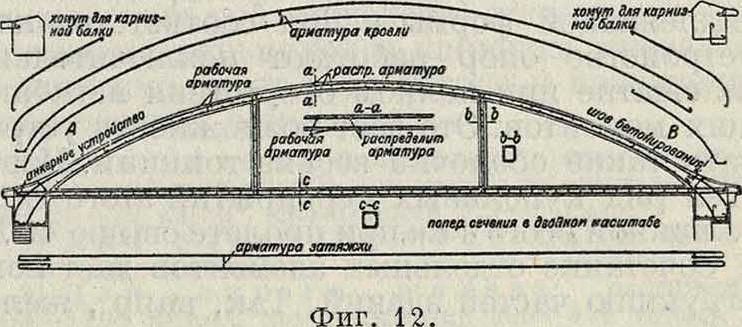
сводом. Работа свода по существу ничем не отличается от работы арки, и расчет в этом случае обыкновенно ведется как для арки шир. в 1 “. В железобетонных сводах допускаются как сжимающие, так и растягивающие напряжения. Сводчатые покрытия применяются без ребер и с ребрами, без затяжек и с затяжками. В мостах пролетное строение составляется часто из отдельных арок.
Рабочая арматура м. б. одиночной и двойной—в зависимости от очертания кривых давления при различных загружениях арки. Верхняя арматура связывается с нижней хомутами из круглого железа. Кроме рабочей арматуры, расположен, параллельно очертанию свода, применяется еще и распределительная, располагаемая параллельно образующим свода. При значительных пролетах и тяжелой нагрузке (в мостах) иногда устраивают арки и своды с жесткой арматурой, представляющей собою клепаный решетчатый остов (система Мелана). В отношении определения напряжений в железе и бетоне арки и своды совершенно аналогичны стойкам, подверженным внёцентренно-м у сжатию.
5. Безбалочные перекрытия. Безбалочными (грибовидными) перекрытиями называются плиты с перекрестной арматурой, непосредственно опирающиеся (без балок) на железобетонные колонны и находящиеся с последними в жесткой связи (смотрите Перекрытия).
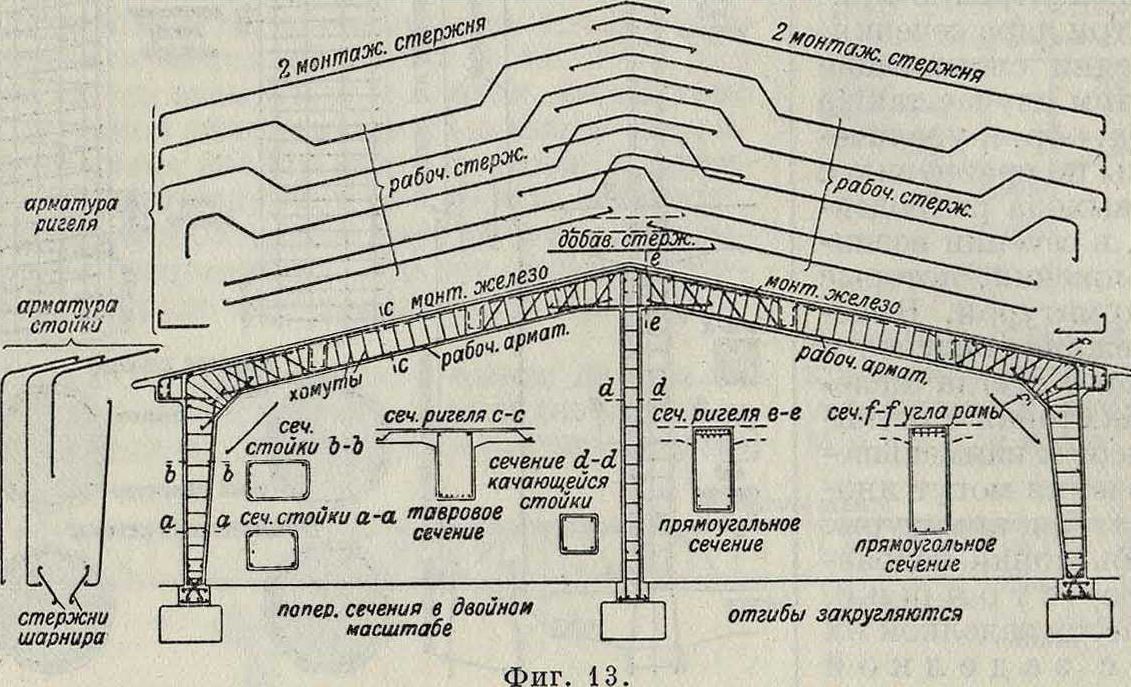
6. Рамы. Рамы (фигура 13) представляют собою сочетания стоек и балок, жестко соединенных между собой, или соединения отдельных жестких стержней (смотрите Рамы). В последнее время весьма крупное значение начинают приобретать т.н.оболочки, дающие возможность перекрытия чрезвычайно больших пролетов. Это—сводчатые или куполообразные плиты, которые при придании им надлежащей формы и при соответственном устройстве опор работают исключительно на сжатие при полном отсутствии изгибающих моментов. Это дает возможность устра-вать такие оболочки весьма тонкими. Известен ряд купольных перекрытий этого типа толщиной всего 4 сантиметров при пролете свыше 40 метров.
Сочетание отдельных элементов дает конструкцию частей зданий. Так, например, железобетонные столбы и балки образуют каркас стен железобетонного здания, а заполнениями фахверка могут служить железобетонные плиты или простенки из другого материала (пустотелые бетонитовые камни и тому подобное.); железобетонные балки и плиты, как уже было указано, дают в соединении железобетонные междуэтажные перекрытия и т. д.
II. Конструктивные требования.
I. Размеры железобетонных элементов.
Плиты перекрытий обыкновенно имеют толщину от 6 см. Более тонкие плиты допускаются только для подвесных потолков, не несущих нагрузки, кроме собственного веса. По германским нормам, плиты с перекрестной арматурой должны иметь полезную высоту, равную не менее 1/30 наименьшего расстояния между опорами (свободно лежащие плиты) или не менее 1/30 расстояния между точками нулевых моментов и во всяком случае не менее 1/40 расстояния между опорами (неразрезные плиты). Для балочных плит вместо J/so берется 1/27. Однако, это ограничение не” вполне обосновано и подчас дает преувеличенные размеры. В гражданских сооружениях толщина плит редко встречается больше 14—15 см.
Прямоугольные балки делаются обыкновенно шириной от Дз до 2/3 рабочей их высоты для возможности размещения арматуры и удобства ее укладки;с другой стороны, для обеспечения надлежащей жесткости, эта высота не должен быть менее 1/20расчетного пролета балки.
Ребристые балки имеют обыкновенно высоту: от1/™ до 7i6 расчетного пролета балки (разрезные) и от 1/идо V25 этого пролета (неразрезные); по отношению к толщине плиты высота балки равна от 4 до 8. Ширина ребра тавра делается не менее 20 см-, ширина принимается равной: для балок большого сечения — от 1/3 до х/2 рабочей высоты ребра, для балок малого сечения—от 7, до 2/з этой высоты; иногда, по архитектурным соображениям, ширине ребра тавра придают размеры в пределах от 1/2 до 1/4 рабочей высоты ребра; нормальная ширина ребер—от 20 до 40 см. Толщина плиты в тавровых балках не должна быть менее 8 см.
Стойкам следует придавать по возможности такое сечение, чтобы наименьший размер их был равен не менее 1/20 высоты и во всяком случае не менее 20 см; лучше наименьшей толщиной стойки считать при обыкновенном армировании 25 см, если бы даже выявленные расчетом напряжения и поверка на продольный изгиб допускали меньшие размеры; в стойках со спиральной арматурой наименьший диам. ядра берется равным 30 сантиметров при наружном диам. в 35 см.
Своды в гражданских сооружениях делаются обыкновенно толщиной от 8 до 15 см. Толщина в ключе бесшарнирных железобетонных мостовых сводов для предварительного подбора сечения м. б. взята где р—постоянная равномерно распределенная нагрузка,q—временная равномерно распределенная нагрузка, г—радиус оси свода, у—объёмный вес, а—допускаемое напряжение в бетоне. Для лучшего обеспечения сов
местной работы плит с ребрами, а в ответственных сооружениях также ребер со стойками, надлежит устраивать у плит, а в надлежащих случаях и у ребер, утолщения (ву-ты) в месте примыкания их к ребрам и стойкам. Начало утолщений берут на расстоянии от оси ребра или стойки не меньшем 1/10пролета плиты или балки; уклон вутов делается не более 1:3. Указанные выше наименьшие размеры обусловливаются практическими соображениями. Действительные же (больше указанных) размеры определяются статическим расчетом в зависимости от действующих сил.
2. Размеры арматуры и ее расположение.
Расстояние в свету между рабочей арматурой и наружной поверхностью бетона не должен быть менее 10 миллиметров в чистоте для плит и стен без хомутов и не менее 20 миллиметров для балок и колонн. Наружная поверхность хомутов не должна отстоять от поверхности бетона менее чем на 10 миллиметров в чистоте. Для сооружений, подверженных действию сырости, кислот, дыма, газа и тому подобное., и для сооружений, представляющих особую опасность в пожарном отношении, указанные расстояния увеличиваются не менее чем на 10 миллиметров.
Расстояние между отдельными стержнями арматуры должен быть достаточным для удобного заполнения форм и полного облегания железа бетоном. В виду этого расстояние в свету между параллельными друг к другу стержнями рабочей арматуры берется не менее диаметра самого стержня и не менее 25 миллиметров. Наибольшее расстояние между стержнями рабочей арматуры — 250 миллиметров. В местах наибольших моментов расстояние между стержнями арматуры плиты не должно превосходить 150 миллиметров.
В частях, подверженных сжатию, в частности в колоннах, поперечная (связывающая основную) арматура должна располагаться на расстоянии, не превосходящем минимального поперечного размера и 10-крат-ного диаметра продольных рабочих стержней арматуры. Расстояние между витками спирали (шаг спирали) должно быть менее 1/5 диаметра ядра и не доля-сно превосходить 80 миллиметров.
В распределительной арматуре и в хомутах расстояние между отдельными стержнями должен быть не более тройного расстояния между прутьями рабочей арматуры и не более 300 миллиметров. Поперечная распределительная арматура должна составлять не менее 15% рабочей арматуры. При этом распределительные стержни надлежит связывать с рабочей арматурой особой отожженной проволокой.
Диам. рабочей арматуры должен быть: для плит в гражданских сооружениях не менее 7 миллиметров, для плит в искусственных сооружениях— не менее 8 миллиметров, для балок в гражданских сооружениях—не менее 10 миллиметров, для балок в искусственных сооружениях—не менее 12 миллиметров, для колонн—не менее 14 миллиметров (железо с диам. менее 14 миллиметров не должно применяться вследствие незначительной в таком случае жесткости железного остова). Для хомутов следует принимать диам. железа в колоннах и балках 6—10 миллиметров. Монтажное железо берется диам. 10—16 миллиметров (в зависимости от размеров балки и характера монтажа). Кольцевая и спиральная арматура для колонн с обоймой берется обыкновенно диам. от 10 до 18 миллиметров.
Если стеряши рабочей арматуры в плите идут параллельно ребрам, то поперек последнего располагается арматура в количестве не менее 8 стержней диам. 6 миллиметров на 1 п.м. Рабочая арматура ребра связывается с телом бетона подвесками или хомутами; концы ее должен быть укреплены в теле бетона крюками Консидера с загибом по диам. в свету, не меньшему четырехкратного диам. сгибаемого стержня и с прямым участком за загибом длиной в 5 диам. На сгибах арматуры, в пределах рабочей ее части, радиус загиба должен быть не менее 10 диам. стеряшя. Концы арматуры по возможности заводят и закрепляют в сжатой части бетона. Особое внимание должно быть обращено на установку хомутов в местах перегибов арматуры; предельное расстояние между хомутами должно быть не более ширины ребра и не более 15 диам. рабочей арматуры.
Устройство стыков арматуры допускается в виде исключения, с расположением их в разбивку и в менее напряженных местах арматуры. При устройстве стыка внахлестку концы растянутых стержней загибаются крюками и заходят один за другой не менее чем на 30 диам., а самые стержни перевязываются накрепко тонкой проволокой. В сжатых элементах насыщение арматурой должен быть в пределах 0,5—3,0%.
3.Температурные швы. Для устранения возможности появления трещин от температурных и усадочных деформаций, а также сдвигов при неравномерной осадке опор, в железобетонных сооружениях делаются сквозные (сверху донизу) разрезына расстоянии не более 40 метров друг от друга для свободного движения разделяемых ими частей. Размер отверстия температурных швов (зазор) зависит от расстояния между швами и от предполагаемой величины деформаций. При средней t° возведения сооружения в общем случае достаточно сделать зазор от 20 до 25 миллиметров. В большинстве случаев зазор заполняют эластичной прокладкой. Если постройка ведется при сравнительно низкой ί°, то зазорам швов придают большие размеры, имея в виду большее расширение конструкции летом и возможность смыкания шва.
III. Допускаемые напряжения для железобетона.
По различным нормам (Госплана, НКПС, московского губ. инженера), допускаемое напряжение варьирует в широких пределах, в зависимости от рода бетона и назначения сооружения, а именно:
1) Д ля бетона: простое центр, сжатие—от 15 до 60 килограмм/см2; при изгибе или изгибе со сжатием: сжатие 20—70 килограмм/см2, скалывание 2,5—8 килограмм/см2.
2) Для сцепления бетона с желе-з о м: 2,5—9 килограмм/см2.
3) Д л я литого железа: растяжение
500—1200 килограмм/см2, перерезывание 500—900 килограмм/см2.
По германским нормам (1925 год), для нормального цемента и нормального железа установлены следующие предельные нормы:
1) Для бетона: центр, сжатие не свыше
35 килограмм/см2; сжатие при изгибе—не свыше 50 килограмм/см2; скалывание при изгибе—не свыше 4 килограмма 1см2.
2) Для сцепления бетона сжеле-з о м—не свыше 5 килограмм/см2.
3) Д ля литого железа: 1200 килограмм/см2.
IV. Основы расчета железобетонных конструкций.
Для того чтобы в железобетоне была полная связь между его составными частями (железом и бетоном) и не происходило скольжения железа в бетоне, деформации как бетона, так и железа должен быть одинаковы. В виду этого должно существовать следующее соотношение между модулями упругости железа Ef и бетона Еъ и напряжениями железа nf и бетона п (в одном и том же месте поперечного сечения):
п _ Ilf
откуда
Et
.=-4-ί Еь
(1)
Напряжения составных элементов железобетона в одном и том же месте относятся между собой, как их модули упругости; поэтому железобетон в отношении воздействия на него возникающих в каком-либо его поперечном сечении нормальных напряжений м. б. заменен однородным материалом (бетоном), если поперечное сечение другого основного материала (железа) ввести в расчет в т раз увеличенным, то есть взять
F=Fb + mf, (2)
где F—приведенная площадь поперечного сечения (площадь однородного тела), Fb и /—соответственно площади поперечного сечения бетона и железа. Положение ц. т. приведенной площади поперечного сечения F определится из выражения:
Vl =
mf
Fb+ mf
У,
(3)
где Ух—расстояние ц. т. площади Р от ц. т. площади Fb, у—расстояние ц. т. площади Fb от ц. т. площади f. Момент инерции I приведенной площади поперечного сечения
1= 1ь +Ebyl + m{If + fyl) — 1Ь + mlf +
+ ViyFb > (4)
где 1Ь и If—соответственно моменты инерции площадей Fb и f, отнесенные к осям, проходящим через их ц. т.; у2—расстояние ц. т. площади от ц. т. площадиF, то есть у2—У—Ух· При симметричной армировке (по отношению к оси поперечного сечения бетона) все три ц.т.совпадут,и мы получим: I =Ib+mIf.
Модуль упругости Еъ, однако, не только различен для разного бетона (разного состава и возраста), но изменяется и в соответствии с изменением величины напряжения, а также в зависимости от знака напряжения в бетоне (растяжение или сжатие); поэтому расчет Ж. к. при изгибе, производимый на основании закона Гука (Hook) для .нек-рого среднего значения Ёь и гипотезы Бернулли относительно сохранения плоскостности поперечных сечений, даст в результате во всех случаях лишь приближенное значение для определяемых напряжений. В железобетонном сечении надо различать три стадии (фазы) напряженного состояния.
Фаза I. Сечение бетона воспринимает как сжимающие, так и растягивающие напряжения и, следовательно, работает полностью. Благодаря малому сопротивлению бетона растяжению это напряженное состояние может иметь место только при весьма малых напряжениях.
Фаза II а. В растянутой зоне бетона начинается образование трещин, однако он еще принимает иек-рое участие в передаче растягивающих напряжений.
Фаза II. Трещины в бетоне достигают нейтральной оси, сопротивление его растяжению полностью исчерпано. Все растягивающие напряжения воспринимаются целиком железом. Очевидно, практическое значение может иметь только фаза II, почему она и принимается в основу расчета железобетонных элементов, в которых наряду со сжимающими могут возникать и растягивающие напряжения. В исключительных случаях производится расчет и по фазе I, причем модуль упругости бетона в сжатой и растянутой зонах принимают одинаковым, хотя новые нормы как русские, так и иностранные исключили требование такого расчета.
В самом общем случае, при учете растяжения в бетоне, положение нейтральной оси и напряжение в бетоне определяются из двух ур-ий статики: суммы проекций всех сил стержня и суммы статическ. моментов всех сил относительно нейтральной оси в связи с уравнениями упругости, устанавливающими связь между напряжениями и деформациями. Оба указанные уравнения приводятся к следующему виду:
п (Sa-mxSz-mSf)^- ) ^
n(Id + mtIz+mIf)=М j
где п—напряжение сжатия в волокне бетона на расстоянии единицы от нейтральной оси; /S—статич. моменты и I—моменты инерции относительно нейтральной оси сечений сжатого бетона, растянутого бетона и железа (индексы d, z и /); —отношения модулей упругости бетона при растяжении и сжатии, т—то же для железа и бетона при сжатии; Р—сумма всех внешних сил, параллельных оси стержня; М—момент всех внешних сил относительно нейтральной оси; φ—коэфф-т продольного изгиба. Следует заметить, что оба указанные ур-ия действительны лишь при условии, если плоскость внешних сил проходит через главную ось инерции, что обычно бывает в большинстве практических случаев. Оба эти ур-ия дают возможность определить положение нейтральной оси и напряжения сжатия в бетоне. Все остальные напряжения определяются из условия пропорциональности их расстояниям от нейтральной оси умножением соответственных величин на коэфф. тх для растянутого бетона и т—для железа:
п=пе ; пх=viх пе ; Uf=m nef. (6)
Таким образом, уравнения для сложного железобетонного бруса вполне аналогичны уравнениям, получаемым для однородного бруса, отличаясь от последних лишь наличием коэффициентов тг и т, которые для однородного бруса равны единице.
V. Расчет на сжатие железобетонных стоек.
Центральное сжатие. Опорные стойки рассчитываются на центральное сжатие по следующим формулам. а) Продольная арматура и обыкновенные хомуты (фигура 14).
Насыщение бетона арматурой α= у5
Приведенная площадь F=Fb (1 + та). Условное напряжение бетона на сжа-
р тие п =
ψΡ
Условное напряжение железа на сжатие Ид=тп.
(7)
Коэфф. ψ вводится согласно нормам. Величина а не должна превышать 0.03.
б) Кольцевая и спиральная арматура (бетон в обойме, фигура 15). Приведенная площадь
-Р1=-Fi + 15 /х + 36 /s, (7a)
где FK—площадь ядра стойки со спиральной арматурой, /s—приведенная площадь кольцевой или спиральной арматуры. Наиболь-
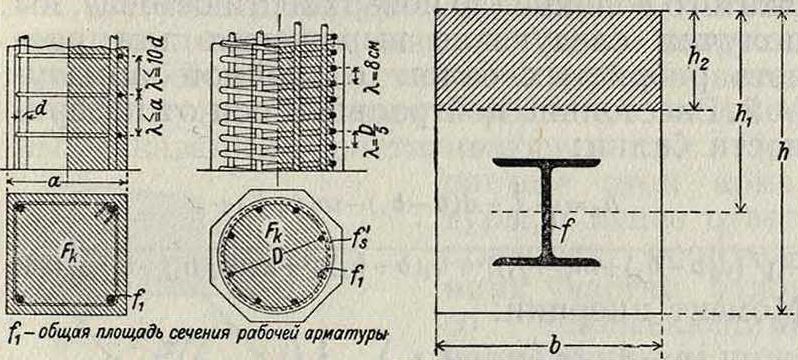
Фигура 14. Фигура 15.
Фигура 16.
шее значение F^2Fb, где Fb—полное поперечное сечение бетона. Величина /„ определится из ф-лы:
U=-ψ, (8)
где fs—площадь сечения железа кольцевой или спиральной арматуры, s — шаг спирали или расстояние между кольцами, D — диаметр ядра.
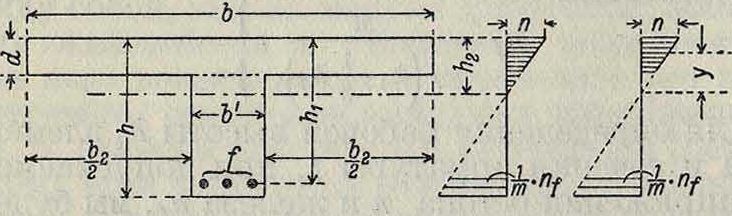
VI. Изгиб железобетонных плит и прямоугольных балок при одиночной арматуре (в вытянутой зоне).
с гибкой арматурой в растягиваемой зоне в формуле (10) надлежит приравнять величину If нулю.
2. Обыкновенная гибкая арматура. Расчет по фазе II (фигура 17). При тх=0 и If—0 получим из ур-ий (9) и (10):
ь -ПИ
- h
2bht
mf
-i
)А +
I=mf(h1- h2)(hx- b,^
К
(jii з fts)
(11)
где I—момент инерции приведен, сечения. Краевые напряжения определятся по ф-лам: для бетона
2 м п=-
bh.
для железа
(*·-!*·)
пг м
(12)
Для определения рабочей высоты hx элемента и сечения арматуры /, при допускаемом напряжении бетона п и железа nf, мы будем иметь формулы:
f=c2Vm
(13)
Коэфф-ты C1 и С2 м. б. вычислены заранее для различных величин допускаемых напряжений и определенного ж и приведены во всех курсах по железобетону и в справочниках. Для проверки сечений элементов служат формулы (11) и (12); для определения же размеров—формулы (13).
3. Двойная арматура. Расчет по фазе II (фигура 18). Обозначим через f сечение сжатой арматуры, f—сечение растянутой арматуры, ах—расстояние от ц. т. сжатой арматуры до крайнего сжатого волокна (до поверхности) бетона, hx—расстояние от ц. т.
На поперечное сечение действует лишь изгибающий момент М.
I. Общее решение (фигура 16). Примем следующие обозначения: h—высота балки; Ь— ширина балки; f—площадь поперечного сечения железа; If—момент инерции поперечного сечения железа относительно оси, проходящей через его ц. т.; hx—расстояние ц. т. железа от верхнего края сжатой зоны бетона (полезная высота балки); h2—расстояние нейтральной оси от верхнего края сжатой зоны бетона. В этом случае положение нейтральной оси определяется из одного основного уравнения (5), дающего, так как Р—0, Sd — m1Sz — mSf=0,
или
* b(l — тх)Щ + (injbh + mf)h2 —
— Q mbh2+mfh^=0. (9)
Второе уравнение (5) в связи с первым (5) дает:
η=М : 1mjb(h — h2)°h +
+ m[lf + f(kl-h2)(h1-i-h2J ). (10)
Вычислив h2 и n, определяют краевые напряжения по ф-лам (6). Для балок и плит
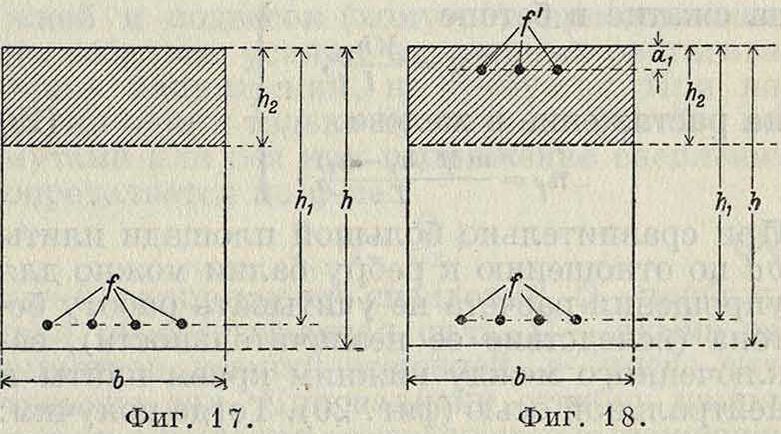
растянутой арматуры до крайнего сжатого волокна (до поверхности) бетона, h—высоту элемента. Пользуясь основной формулой (5) мы получим при Sd — rnSf^0 следующие выражения:,
К=[ж( + /) +
+ Vm f + /)2 + 2m(fhx + fajb] (14)
I=l2(hx - з h^bhl + mf(hx- ax) (h2 - ax)
4. Жесткая арматура. Если h—высота прямоугольной балки, b — ее ширина, f — площадь поперечного сечения арматуры, If — момент инерции поперечного сечения железа относительно оси, проходящей через его ц.т.
h1—рабочая высота балки и если не учитывать сопротивления бетона на растяжение (расчет по фазе II), то положение нейтральной оси определится из равенства:
Κ=-ψ + |/~|(dff + 2m b ’ (15)
а момент инерции приведенного сечения будет равен
I=m [^+ /(*!-fea)(fcx—|ft2)]. (16)
5. Учет растягивающих напряжений в бетоне. Для прямоугольных балок пользуются ф-лами (9) и (10), принимая в них тг=1.
VII. Расчет ребристых балок.
I. Одиночная арматура. Сопротивление бетона на растяжение не учитывается (фигура 19). С принятыми на фигуре 19 обозначениями и
f-общая площадь сечения арматуры
Фигура 19.
Фигура 20.
если /— площадь поперечного сечения арматуры в растянутой зоне бетона, мы получим следующие формулы для расчета ребристых балок с одиночной арматурой. Положение нейтральной оси определится из выражения:
-d(b-b1)-mf +
_._;_i
+1/[d (b- b1)+mff+ d2bj (b - ЬУ)+ 2mfhlb1 f. (17) Момент инерции приведенного сечения I=ftftj^-ift,)-
Напряжения: на сжатие в бетоне п =:
Miis
(18)
(19)
на растяжение в железе тМ (hi - h2) nf - i
При сравнительно большой площади плиты bd по отношению к ребру балки можно для упрощения расчета не учитывать работу бетона (вследствие ее незначительности), заключенного между нижним краем плиты и нейтральной осью (фигура 20). Тогда получим:
~ btP + mfh!
расстояние ц. т. сжатой зоны от нейтральной оси (фигура 20):
d2
Напряжения: в железе в бетоне
6 2/i2 - d
м
(hx - h2 + y)
(21)
(22)
nf
ii, - iis
Если получается h2>d, то нейтральная ось пройдет через плиту ребристой балки, и по следняя рассчитывается тогда как прямоугольная балка шириною b и высотою h.
2. Двойная арматура. Сопротивление бетона на растяжение не учитывается (расчет по фазе II) (фигура 21). С принятыми на фигуре 21 обозначениями, которые означают: /—площадь поперечного сечения растянутой арматуры;/!— площадь поперечного сечения сжатой арматуры; fej— расстояние от ц. т. растянутой арматуры до крайнего сжатого волокна (до поверхности бетона); аг—расстояние от. ц. т. сжатой арматуры до крайнего сжатого волокна (до поверхности бетона), мы получим следующие выражения для расчета ребристых балок с двойной арматурой. Расстояние нейтральной оси от поверхности балки:
= — d(b-bl)-m(f+f1)+
+i [d(b-b1)+m(/-t-/1)]a+b1(b-b,)d!+2mb1(ii1/+a1/1)j(23)
Момент инерции:
I=bh (ftx -1 ht) -1 (ft, - d)2b x x (fcj- ί h2 - 3 d)+ m/х (ftx - «О (fe2 - a2). (24)
-A.:
«
"t"
| b U * | ||||
| • · ·-
f, |
У | Ί | ||
| -ь | ~-bг~
Г |
|||
| ___ | ||||
f- общая площадь сечения растянутой арматуры ФИГ. 21.
VIII. Скалывающие и главные растягивающие напряжения.
I. Учет скалывающих и главных растягивающих напряжений. Помимо определения нормальных (рассмотренных выше) напряжений, в Ж. к. должны быть также выявлены скалывающие напряжения. Для подверженной изгибу балки скалывающее напряжение в нейтральной оси будет равно Q i
t _ QS _ lb ~
(25)
где Q—поперечная сила в рассматриваемом поперечном сечении; £—статич. момент сжатой или растянутой зоны относительной нейтральной оси; I—момент инерции активного поперечного сечения; b—ширина балки в нейтральной оси; z—плечо пары внутренних сил. Скалывающее напряжение в поперечном сечении бетона с нерабочей растянутой зоной (расчет по фазе II) остается до железной арматуры постоянным и должен быть воспринято сцеплением бетона с арматурой. Величина z в формуле (25) равна (при принятых в пп. VI и VII обозначениях): для прямоугольного сечения с одиночной арматурой
z=К - g h2,
для прямоугольного сечения с двойной арматурой и для ребристых балок при учете напряжения сжатия в ребре = I Z nf(h1-h!s) ’
где вместо I должен быть вставлено соответствующее из вышеприведенных выражений. При не-учете напряжений в ребре z=- h2 + у. тона напряжение (4 килограмма/см2); поэтому здесь обычно нет необходимости в специальной арматуре для их воспринятая. В балках такая арматура необходима, т. к. появляющиеся в них скалывающие напряжения обычно выше допускаемых. Наклонные стержни отгибают под углом 45°, имея в виду, что действующие в нейтральной оси поперечного сечения скалывающие напряжения по своему значению равны в рассматриваемом месте направленным под углом в 45° главн. растягивающим напряжениям. В балках главные напряжения у оси не должны вообще превосходить величины 14 к г/см2, в противном случае необходимо увеличить ширину или высоту балки. Совокупность всех внутрен. косых растягивающих сил у оси в балках должна целиком восприниматься наклонными частями арматуры совместно с хомутами, причем не учитываются вовсе сопротивления бетона на растяжение и обыкновенно на отогнутые стержни передается около 2/3вышеуказанных растягивающих сил. При расчете этой арма-t2 туры в менее ответ ственных сооружениях участки балок со скалывающими напряжениями ниже допускаемых не принимаются в расчет. Специальной проверки на скалывание бетона и на сцепление бетона с желе-фигура 22. 30м ПРИ этом не про изводится. Если в 2 поперечных сечениях, которые находятся на расстоянии λ друг от друга, максимальные скалывающие напряжения равны ^и ί2, то главные растягивающие напряжения им равны, но распределяются только на длину у-= (фигура 22). Поэтому приходящееся на длину λ главное растягивающее усилие будет равно
V-./V6 (26)
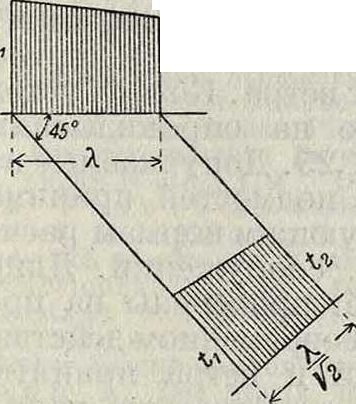
Z=-
2. Распределение хомутов и отогнутой арматуры. Распределение противодействующей скалыванию арматуры м. б. сделано
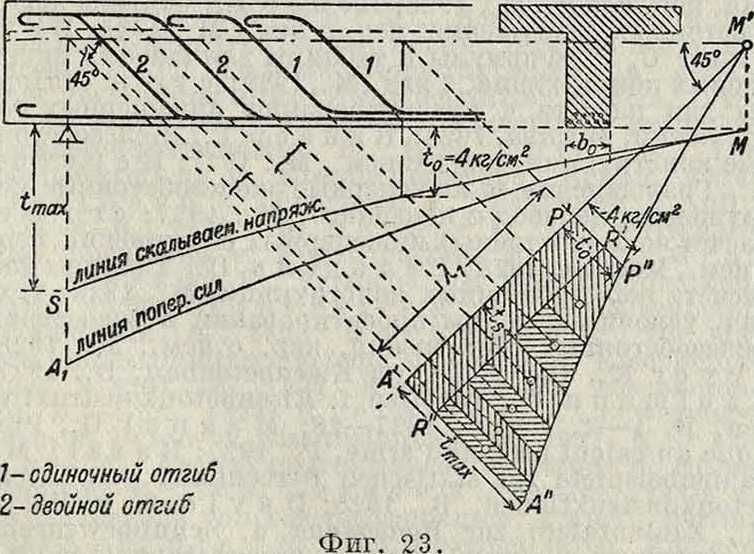
графически следующим построением (фигура23). Вычерчивают линию поперечных сил МАги отвечающую ей линию скалывающих на пряжений MS, ординаты последней
OqZ
откладывают затем от линии ΜΆ, проходящей через точку М под углом 45° к оси балки; точка М лежит на нейтральной оси балки и отвечает нулевому значению поперечной силы. Если затем от полученной площади МАА" напряжений отрезать площадь МРР" с наибольшей ординатой t0==4 килограмма/см2, то остальная площадь ΡΡΆ Ά" определит главные растягивающие усилия, не могущие быть воспринятыми одним бетоном. Хомуты воспринимают величину ts. При общем поперечном сечении всех ветвей хомутов fs и допускаемом их напряжении на растяжение nf, расстояние между хомутами определяется из ур-ия:
е=Ш. ί27ι
Принимая линию А"Р" за прямую, получим главное растягивающее усилие:
nf — д ^ ^
где —длина отрезка АР. Необходимое число стержней к для воспринятая этого усилия определится из равенства:
fc=,V (28)
где /—поперечное сечение одного отогнутого стержня; —допускаемое напряжение железа. Чтобы найти расположение отдельных стержней в балке, площадь растягивающих напряжений A"P"RR", оставшуюся после вычета напряжений fs, воспринимаемого хомутами, делят на к равновеликих по площади частей (фигура 23). Ц. т. найденных частей определяют места отгиба стержней. Последние заворачивают в верхней части балки в сторону опор и заканчивают крюками. Хомуты располагают по всей длине балки независимо от данных статического расчета.
3. Расчет напряжений сцепления. Проверки сцепления при наличии отогнутых стержней и подвесок (хомутов), принимающих на себя все усилия от главных растягивающих напряжений, не требуется. При наличии одних только прямых стержней с хомутами или без них напряжение сцепления определяется по ф-ле:
(29)
t — — h~Uz’
где ij—напряжение сцепления, Q—наибольшая перерезывающая сила, U — сумма периметров сечений стержней, z—плечо внутренних сил. При наличии отгибов напряжения сцепления определяются выражением i Q
ίι =
2 Uz
(30)
Некоторые нормы требуют расчета по этой формуле при диаметре стержней арматуры большем 25 миллиметров.
IX. Расчет на сжатие и изгиб.
В том случае, когда осевая внецентренная сила Р не выходит из ядра сечения, напряжения по всему сечению остаются одного знака (сжатие) и краевое сжатие бетона определяется формулой:
Р 7, Рее
- 9F к ± Т~ (31)
Здесь F и I —площадь поперечного сечения приведенного сечения и его момент инерции относительно оси через ц. т., с—эксцентриситет, е—расстояние от ц. т. до крайнего волокна, к—отношение допускаемых напряжений на сжатие при изгибе и при чистом сжатии. Германские нормы допускают пользование для расчета этой ф-лой и при силе, несколько выходящей из ядра сечения, когда вычисленное по ней наименьшее краевое напряжение получается отрицательным (растяжение), но не превышает допускаемого напряжения на сжатие. В противном случае необходимо переходить к расчету, в котором сопротивление бетона растяжению не учитывается. Существующие русские нормы требуют этого во всех случаях, когда сила Р выходит из ядра сечения и, следовательно, в сечении появляется растяжение.
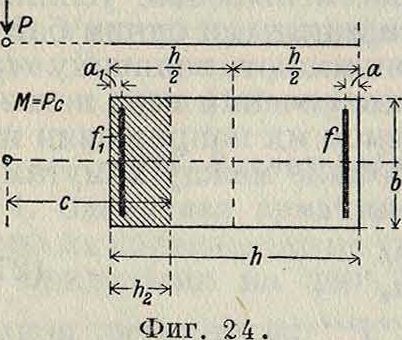
Основными ур-иями служат ур-ия (5), в которых надо принять т1=0. При прямоугольном сечении и двойной арматуре и при обозначениях, принятых на фигуре 24, путем исключения п из обоих уравнений (7) получается уравнение для определения положения нейтральной оси
fe2-3fel(|-c) + Vir[/(e+ ^~α) +
+ /i(c-2 + ffli)]=x[/(fe-«)(°+ 2~α) + + /i«i(e-2 + ai)j ‘ (32)
Указанное кубич. ур-ие проще всего решается одним из методов постепенных приближений, например по методу Ньютона. Величину п определяют затем из одного из ур-ий (5). Краевые напряжения получатся из ур-ий:
п=nh2; rif — mn (h — a— fe2) ;
nfi=mn (fe2 — «i). (33)
Определение напряжений значительно упрощается при симметричной арматуре, когда f—fx, или при одиночной, когда /х= 0.
Аналогичным же способом можно вывести ф-лы и для таврового сечения. При более сложных сечениях рекомендуется применение графич. методов, например метода Гвиди.
Для подбора сечений при изгибе со сжатием лучше всего пользоваться многочисленными составленными для этого графиками и таблицами, из которых можно назвать графики Мёрша, таблицы Залигера, Купце, Везе и других.
Случай изгиба и растягивающей силы решается совершенно аналогично, причем ф-лы получаются из вышеприведенных путем замены +е на —с.
Для подбора сечений прямоугольных балок, которые работают на сжатие и изгиб, рекомендуется при данных Р и М и принятой ширине балки b пользоваться таблицами Купце (Kunze).
X. Расчет подмостей и форм.
Подмости и формы должен быть так рассчитаны, чтобы они давали лишь малую просадку при нагрузке бетонной массой при достаточной прочности, жесткости и устойчивости. Упругий прогиб форм не должен превышать 1/400их свободного пролета, а упругий прогиб подмостей—γ1000 пролета, считая модуль упругости дерева 110 000—120 000 килограмм/см2. При возведении подмостей и форм им придают предварительный строительный подъем от V1000 Д° 7ωο пролета и более, чтобы избежать провеса готового сооружения; этот подъем должен быть согласован с ожидаемым упругим прогибом и начальной просадкой при нагрузке бетонной массы.
Для учета динамич. напряжений, возникающих при трамбовании или быстром вливании бетона, необходимо принятый при расчете форм вес бетонной массы увеличить в Н/а раза. Горизонтальный распор сырого бетона м. б. определен по ф-ле:
р=0,035 h, (34)
где р—горизонтальное давление в килограммах/см2 на глубине h т. При расчете подмостей следует принимать нагрузки: от собственного веса вспомогательн. приспособлений (800 килограмм/м3), от толпы рабочих (100—200 килограмм/м2), от веса частей сооружения и от ветра. Коэфф. устойчивости при проверке на опрокидывание принимается не менее 1,25. Допускаемые напряжения при расчете подмостей принимаются согласно существующим нормам расчета временных деревян. сооружений. Длинные сжатые части должен быть проверены на продольный изгиб. При одновременном действии вертикальной нагрузки и ветра принятые при расчете подмостей допускаемые напряжения м. б. повышены на 15%.
Лит.: Богуславский II., Железобетон, Л., 1925; Ж е р н о к о в II., Расчет железобетонных элементов, Л., 1926—27; 3 а л и г e р Р., Железобетон, его расчет и проектирование, перевод с нем., 2 изд., М.—Л., 1928; Кашкаров Н., Графнч. таблицы для расчета железобетонных сооружений, М., 1926; Л а х т и н Н. и Кашкаров Н., Железобетон, М., 1925 — 27; Лолейт А., Курс железобетона, 2 издание, М. — Л., 1928; Лун и н Б., Железобетон, М.—Л., 1 927; М о л о т и л о в Н., Таблицы для расчета железобетонных конструкций, Томск, 1926; Ф р а н к В., Железобетонные сооружения, Берлин, 1923; П а д л е р Г., Расчеты по железобетону, перевод с немецкого, Москва, 1927; Буданов Н., Железобетон. Теория, М., 1924; Гастев В., Методы и данные для расчета железобетонных конструкций, Л., 1928; Р и в о ш О., Железобетонные конструкции и графики для расчета, ч. 1—2, П., 1921—22; Граф О., Петри В., М б р ш Е., Рут Г., Проектирование и расчет железобетонных сооружений, пер. с нем., М„ 1928; Бейер К., Статика железобетонных сооружений, пер. с нем., М., 1928; Брилинг С. Р., Формулы и таблицы для расчета инженерных конструкций, 2 изд., М., 1929; его ж е, Нормы для расчета и проектирования инженерных сооружений, Москва, 1928; Кайзер Г., Железобетонные конструкции, пер. с нем., М. 1927; Керстен К., Гражданские и инженерные железобетонные сооружения, перевод с немецкого, М., 1927; его же, Расчет железобетонных инженерных сооружений, пер. с нем., Москва, 1928; Г е л ь д е л ь П., Таблицы для расчета железобетонных конструкций, М., 1928; Техник. условия и нормы проектирования и возведения железобетонных сооружений, пер. с нем., М., 1928; В еу ег К., Die Statik im Eisenbetonbau. В., 1927; Kaufmann C., Tabellen f. Eisenbetonkonstruktio-nen, В. 1—2, Berlin, 1927—28; Magnel G., Pratique du calcul du bdton агтё, P., 1927; В а г a 1 i M„ Zahlenbeispiele zur statischen Berechnung von Eisen-betonkonstruktionen, B., 1925; David L. u. Perl H., Zahlentafeln zur Bemessung d. Schubbewehrung v. einfachen u. durchlaufenden Eisenbetonbalken, B., 1926; Graf O., Petry W., MorschE., Ruth G., Entwurf u. Berechnung v. Eisenbetonbauten. Ein Handbuch, bearb. v. O. Graf u. andere, В. 1, Stuttgart, 1926; G 61 del P. Zahlentafeln zur Bemessung von beliebig gelagerten Eisenbetonplatten u. Balken,
2 Aufl., В., 1926; H e r z к a L., Schwindspannungen in Tragern aus Eisenbeton, Lpz., 1925; KcrstenC., Der Eisenbeton, T. 1—3, B., 1925—27; К 1 e i η 1 o-g e 1 A.,Veranschlagen v. Eisenbetonbauten, 3 Auflage, B., 1926; M 6 r s c h E., Der Eisenbetonbau, В. 1—2, Stg., 1923—28; Paller G., Grundlagen f. d. prak-tischen Eisenbetonbau, Berlin, 1926; Eiepert P., Eiementare Einliibrung In d. Eisenbetonbau, T. 1—2,
5 Aufl., Berlin, 1924; S a 1 i g e r R., Der Eisenbeton,
5 Aufl., Lpz., 1925; Otzen R., Der Massivbau, B., 1926; Botim F., Das Betonieren bei Frost, B., 1928;
B ii c b i F., Die Massenberechnung im Eisenbetonbau, B., 1929; Olsen H., Die wirtschaftliche u. konstruk-tive Bedeutung erhohter zulassiger Beansprucbungen f. d. Eisenbetonbau, B., 1928; Boost H., Beton- u. Eisenbetonbau, Darmstadt, 1920; Grabowski K., Formanderungsarbeiten d. Eisenbetonbauten bei Bie-gung, «Forscherarbeiten auf der Gebiete des Eisen-betons», B., 1906, H. 4; Bosch J., Berechnung d. gekreuzt armierter Eisenbetonplatten und deren Auf-nahmetrager unter Beriicksichtigung d. Kraftwirkun-gen nach zwei Richtungen, ibidem, 1908, H. 9; D a-n u s s о H„ Beitrag zur Berechnung d. kreuzweise be-wehrten Eisenbetonplatten u. deren Aufnahmetrager, bearb. Y. H. Bronneck, ibidem, 1913, H. 21; L e i t z M., Die Berechnung d. freiaufliegenden rechteckjgen Piatten, ibidem, 1914, H. 23; Forster M., Die Grundzilge d. Eisenbetonbaues, 3 Aufl., Berlin, 1926; Ilaberkalt K. u. Postuvanschiitz Fr., Berechnung d. Tragwerke aus Eisenbeton, 2 Aufl., W., 1912; Hager K., Theorie d. Eisenbetons, Mch., 1916; Heintel K., Berechnung d. Einsenkung v. Eisenbetonplatten u. Plattenbalken, Berlin, 1909; Jackson A., Ober Spannungslinien mit Anwendung auf d. Eisenbeton, Stuttgart, 1917; Marcus H., Die Theorie elastischer Gewebe u. ihre Anwendung auf d. Berechnung biegsarner Piatten, B., 1924; Marcus H., Die vereinfachte Berechnung biegsarner Piatten, B., 1925; Nldai A. Die elastischen Piatten, B., 1925; Probst E., Yorlesungen iiber Eisenbeton, В. 1—2, B., 1922—23; S a 1 i g e r R., Festigkeit ve-randerlich elastischer Konstruktionen, insbesonders d. Eisenbetonbauten, Lpz., 1904; S aliger R., Schub-widerstand und Verbund in Eisenbetonbalken, B., 1913; Strassner A., Beitrag z. Theorie kontinu-ierlicher Eisenbetonkonstruktionen, B., 1912; T ο η βίο a η n A., Die Statik d. gesamten Hoch-, Tief- u. Eisenbetonbaues, T. 5—Einfiihrung in d. Statik d. Eisenbetonbaues, nebst ausfiihrlichen Berechnungsbei-spielen, Naumburg a/S., 1923; Loser B., Bemes-sungsverfahren. Zahlentafeln und Zahlenbeispiele zu d. Bestimmungen d. deutschen Ausscbusses lur Eisenbeton v Sept. 1925, 2 Auflage, B., 1925; Weese E., Eisenbetonzahlentafeln, T. 1—5, B., 1926—28; Hand-hueh f. Eisenbetonbau, hrsg. v. F. Emperger, Berlin, 1921—28; Graf O., Versuche iiber d. Druekelastizi-tat u. Druckfestigkeit v. Mauerwerk, Berlin, 1924; Abrams A., «Bull, of the Lewis Institute, Structural Materials Research Laboratory», Chicago, ab 1920; Majerl, Die Wirtschaftlichkeit als Konstruktions-prinzip im Eisenbetonbau, Berlin, 1913; A m ar Ch., ThOorie gOndrale et formulaire pratiques du ciment arme, P., 1926; Augros P., Bdton armd, P., 1926; Baudart C., Baton агтё. Tables de calcul des dalles et poutres, P., 1924; Chanson M., Manuel de la construction en ciment et en ciment armi, P., 1925; Spiegel G., Stahl- u. Eisenbeton im Geschoss-grossbau, B. 1928; G e у e r E., Tabellen zur Berechnung v. einfach und dopelt armierten Balken u. Flatten aus Eisenbeton, mit Hilfstafel f. Plattenbalken, Berlin, 1921; Gold el P., Bemessungstafeln fiir Eisenbeton-Konstruktionen, Berlin, 1927; К a η n F., Durchlaufende Eisenbetonkonstruktionen in elastischer Verbindung mit d. Zwischenstiitzen, Berlin, 1926;
K u n z e W., Neue Tabellen f. exzentrisch gedriickte Eisenbetonquerschnitte, B., 1925; Thiel W., Die Arbeitsfestigkelt d. Eisenbetonbalken, Berlin, 1924; Esselborn K., Lehrbuch d. Hochbaues, 8 Aufl., В. 1—2, B., 1923—25; Berger L., Die wirtschaft-liche Bemessung y. Plattenbalken, B., 1928; Graf O. u. Μ о r s c h E., Versuche mit Eisenbetonbalken, Berlin, 1928; Haberstroh H„ Der Eisenbeton im Hochbau, B., 1923; Hartmann F., Die sta-tisch unbestimmten Svsteme d. Eisen- u. Eisenbetonbaues, 2 Aufl., B., 1922; Kayser H., Eisenbetonbau, B.—Lpz., 1923; К 1 e i η 1 о g e 1 A., Bewegungs-fugen im Beton- u. Eisenbetonbau, B., 1927; К 1 e inlog e 1 A., Fertigkonstruktionen im Beton- u. Eisenbetonbau, B., 1928; Lerche K., Aus d. Praxis d. Veranschlagens von Eisenbetonbauten, 2 Aufl., Berlin, 1928; S chi titer II., Der Eisenbetonbau. Rahmen u. Gewolbe, Berlin, 1920—22; «Deutscher Ausschuss f. Eisenbeton», B., ab 1910; «Osterreichischer Ausschuss f. Eisenbeton», W., ab 1912; «Proceedings of the Amcr. Soc. for Testing Materials», Philadelphia; «Teknisk Forenings Tidskrift»,Kjobenhavn;«Baton armd»,P., «Le I
constructeur de ciment arme», P.; «Engineering News-Record», New York; «Civil Engineering», London; «Zeitschriftenschau ftir das gesamte Bauingenieurwe-sen», Berlin. С. Брипинг.