> Техника, страница 46 > Жесткая рама

Жесткая рама

Жесткая рама, конструкция, состоя-ш,ая из стержней, жестко соединенных друг с другом. Отдельные стержни, как исключение, могут присоединяться к другим при помощи шарниров. Ж. р. применяются в строительстве в качестве основных несущих частей для путепроводов и мостов, для перекрытий в зданиях, для фундаментов турбин и тому подобное.; они могут входить в сооружение и как элементы конструкции (например жесткие опорные рамы мостов с ездою по низу). Материалом для Ж. р. может служить сталь (железо), но наиболее широкое применение Ж. р. нашли в железобетоне, к-рому жесткое соединение между собой отдельн. элементов конструкций присуще по самой его природе.

Ж. р. состоят чаще всего из горизонтальных или слабо наклонных стержней (р и-гелей) и из вертикальных или почти вертикальных стержней (стоек). Если оси всех стержней, образующих раму, одна из главных осей инерции каждого сечения этих стержней и все действующие на Ж. р. силы лежат в одной плоскости, Ж. р. называется плоской; если же эти условия не соблюдены, то пространственной. Плоские

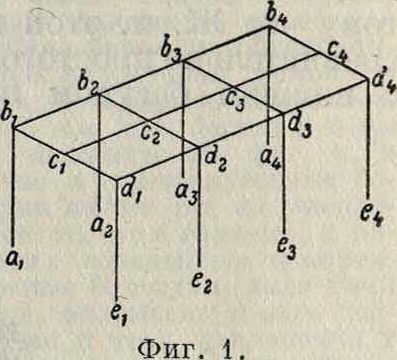
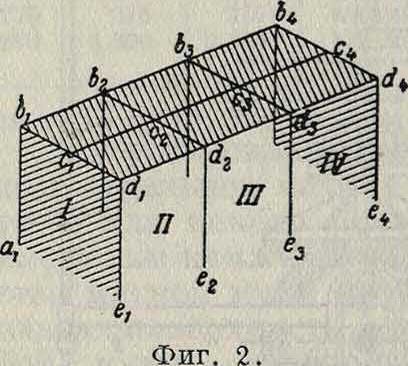
Ж. р. на практике почти не встречаются, однако в целях упрощения пространственные Ж. р. при расчете чаше всего рассматриваются как плоские, работающие независимо друг от друга. Так, Ж. р. типа, изображенного на фигуре 1, часто расчленяют для расчета на плоские жесткие рамы: a₁b₁c₁d₁e₁, и т. д.; стержни Ь^, с_±с, и d^, рассчитывают при этом как неразрезные балки, шарнирно опирающиеся на рамы; иногда кроме рам abode, рассчитывают еще рамы a₁b₁a₂b2a_sb_aa_tb_i и Стой ки ab и de входят при этом в состав двух рам, и потому усилия, полученные для них из обоих расчетов, суммируются. В действительности, благодаря жесткому присоединению стержней bb, сс и dd к стержням bed, последние подвергаются кручению. Жесткая связь стержней между собою обусловливает появление крутящих моментов и в других элементах Ж. р. Еще более ваясную роль может играть связь между отдельными жесткими рамами и другими частями конструкции, создаваемая плитами, монолитно соединенными со стеряснями рам. Если, например (фигура 2), в плоскостях I и IV стоят массивные стены, а в плоскости устроена сплошная плита, монолитно связанная со стержнями рам, то смещение ригелей рам параллельно стенам встречает препятствие со стороны плиты и стен,которые имеют в этом направлении большую жесткость. В таких случаях бли-же к действительности считать, что узлы плоских Ж. p. II и III вовсе не могут смещаться в их плоскости.

В большинстве случаев Ж. р.—статически неопределимые системы; иными словами, внутренние силы, а иногда и опорные реакции их, не м. б. получены при помощи одних только уравнений статики. При расчете Ж. р. обычно пользуются т. н. основной системой; основная система представляет собой либо статически определимую систему

либо такую статически неопределимую, расчет которой имеется уже в готовом виде или требует значительно меньшей затраты труда, чем непосредственный расчет заданной Ж. р. Основная система должна иметь те яге очертания, размеры и жесткость стержней, как и заданная Hi. р., и м. б. получена из по-

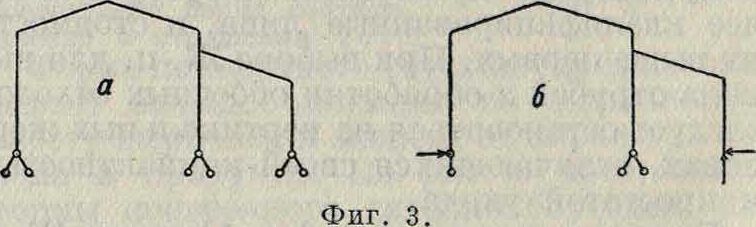
следней либо уничтожением нек-рых связей (отбрасывание опорных закреплений, постановка шарниров, разрезы стержней), либо введением новых связей, либо, наконец, одновременным введением одних и уничтожением других связей. Напр., раму (фигура 3, а) легко превратить в статически определимую данной Ж. р. В частности все перемещения по направлению сил×и усилия в добавочных связях (усилия по направлению перемещений А) должен быть равны нулю. На основании принципа независимости действия сил условия эти можно написать в виде следующих канонических уравнений:

+×2^12		• + Хп“м	+ Δη- ·ιόι,ηΛ·ι		+	• · + Δη- "ΐη^1,η- -Ίη	+ д1гр=0 i
X 1^21 +-&2^22		+ Хпд2п	+ ^П- -1 ^2, W+1	+ Δη- -2^2,η^-2	+ .·	· + ^nJrm^2,nJrm	+ ^2 ,p — 0 [	й 1 ft
*ι*ηι +-^2<5?гг	+ ·	• · + Χηδηη	+ ΔηΛ-1 1	+ ΔΠ- -2^η,η- ·2	+	· + ‘^nJrm^n,nJrm	+ ^η,ν=0	s
*1*п+ы + -^2Я>г+1,2	+	,. + Χηχη+ι,η	+ ^η-Γΐ^Μ+Ι,Μ+Ι	+ Δη- -2χη~{·1 ,η-τ2	+	• · “Ь Δη4-ιηχιι+ΐ ,n-tm + xn-tι,ν — 0		<3
X 1ХП~ -2,1 +×2хП-г2,2	+.	• · + Хпхп~г2,п		+ Δη-Τ-2Χη-ν2,η- -2 + ·		• · + ^п~Ьтхп~}-2,п-Ьт	+ xn+2,p=0 1	ft

!»

X^ 2^xvc w,2 + · · · + Х- п^хп^-т,п. + bi т ^?г+2*^»-Н?г,«+2 + · ·. 4- ^ т^п-ут.п-гт “I ^хп+т,р ⁼ О £

систему (фигура 3,6), превратив одну из ее опор в горизонтально подвижную и отбросив другую. Внутренние силы и перемещения такой системы определяются без затруднений. Раму (фигура 4, а), несущую бункер, деформациями которого благодаря его большей жесткости можно пренебречь, легко превратить в систему балок, заделанных обоими концами. Для этого достаточно воспрепятствовать горизонтальному смещению бункера постановкой горизонтального стеряшя и повороту узла А присоединением к нему жесткой не-поворачивающейся консоли. Концы стержней полученной т. о. системы (фигура 4, б) не могут ни смещаться ни поворачиваться и м. б. рассчитаны как балки, заделанные

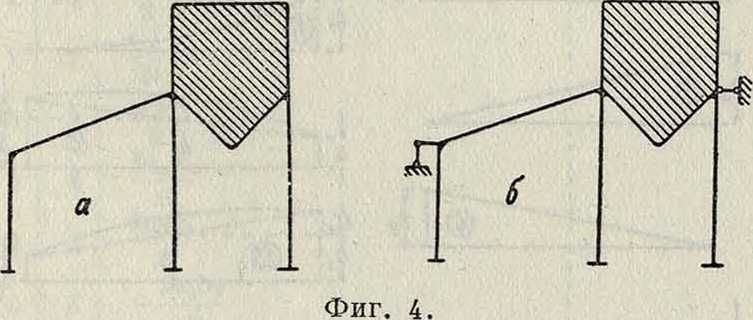
обоими концами. Расчет таких балок на любую нагрузку и оценка влияний смещения и поворота их концов производятся легко и быстро по готовым ф-лам и таблицам. Системы (фигура 3, б и 4, б) могут служить основными системами при расчете Ж. р. (фигура 3, а и 4, а). Во многих случаях основная система получается проще всего комбинацией обоих описанных выше приемов.

Если в основной системе недостает некоторых связей, то взамен их прикладываются неизвестные внешние силы X_lt Х₂., Х_г., Х_к., Х_п; если в основной системе имеются добавочные связи, каждую из них представляют себе на время отброшенной, дают системе неизвестное по величине перемещение А по тому направлению, по к-рому отброшенная связь не позволяла перемещаться, и, вводя обратно связь, закрепляют систему в новом положении. Соответственным подбором сил Хи Х₂,·.·, Х_п и перемещений А_п+1, Л_п+2,., /)_г., А_г., А_п+т можно заставить основную систему работать под влиянием заданной нагрузки, сил×и перемещений А точно также, как работает заданная Ж. р. под одной только заданной нагрузкой. Перемещения основной системы, ее внутренние силы и опорные реакции при этом ничем не будут отличаться от тех же величин для за-

Здесь: <5_а—перемещение по направлению Х{, вызываемое силой Х_к= 1; д,_г—перемещение по направлению Х_и вызываемое перемещением А_г — 1, х_ш—усилие по направлению А/, вызываемое силой Xj.= l; х_и.—усилие по направлению А_ь вызываемое перемещением A_r=l; 8_jp—перемещение по направлению Х_г·, вызываемое заданной нагрузкой; ^xip—усилие по направлению A_lt вызываемое заданной нагрузкой. Число каноиич. ур-ий (и + то) равно числу неизвестных сил и перемещений, а следовательно, достаточно для их определения.

По вычислении всех неизвестных можно определить для любого сечения заданной системы величины поперечной или продольной силы, изгибающего момента, угла поворота или прогиба, суммируя влияния на основную систему вычисленных уже сил X, перемещений А и нагрузки, на к-рую требуется рассчитать заданную Ж. р. Изгибающий момент в сечении s, например, равен

M_s=M_S1×i Н- M_S2X₂ +. + M_snX_n +

+ M_S:n+iA„₊₁ + M_s>n+2A_n+2 +. +

“b s ,n+mA n-rm 4" ^sp ’

где M_s — изгибающий момент в сечении s заданной системы, вызываемый нагрузкой; M_st — изгибающий момент в сечении s основной системы, вызываемый силой Х_г=1; M_sr—изгибающий момент в том же сечении основной системы, вызываемый перемещением A_r=1, и M_sp—изгибающий момент в том яда сечении основной системы, вызываемый заданной нагрузкой. Расчет Ж. р. сводится, т. о., к расчету основной системы. В качестве элементов основной системы моя-г-но пользоваться не только статически определимыми системами и балками, заделанными на обоих концах или на одном конце; для этой цели пригодна вообще любая такая система, которая при помощи простейших приемов или готовых таблиц и ф-л м. б. легко рассчитана на любую нагрузку и на каждое из смещений ее концов и опор, которым ее приходится подвергать в процессе расчета заданной Ж. р. Нек-рые Ж. р. добавлением одной дополнительной связи удается превратить в неразрезные балки на упруго поворачивающихся опорах (смотрите Балки неразрезные). Такой неразрезной бй можно воспользоваться как основной системой, рассчитав ее, кроме заданной нагрузки, еще и на боковое смещение ее ригеля. Вообще же основная система должен быть выбрана т. о., чтобы число неизвестных было возможно меньше. чтобы возможно большее число коэффициентов канонич. ур-ий обращалось в нуль и чтобы коэфф-ты, не обращающиеся в нуль, определялись возможно проще. Чтобы с удобством пользоваться в качестве элементов основной системы статически неопределимыми однопролетными балками, необходимо озаботиться неподвижностью тех узлов основной системы, к которым эти балки примыкают. Поэтому приобретает особое значение вопрос о возможных упругих перемещениях узлов

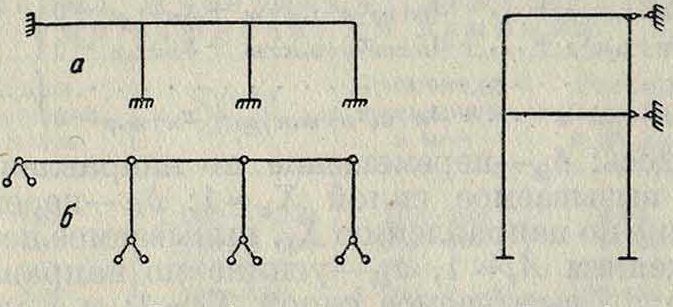
Фигура 5. Фигура 6.

рамных конструкций. Деформациями, зависящими от продольных сил, и тем более изменением расстояний между узлами вследствие искривления соединяющих эти узлы первоначально прямых стержней обычно пренебрегают, а расстояния между узлами рам, соединенными прямыми стержнями, принимают поэтому неизменными. Для определения возможных перемещений узлов рамы надо во всех узлах и во всех точках перелома стержней поместить шарниры и исследовать перемещения полученной т. о. шарнирно-стержневой системы. Шарнирная схема Ж. р. может оказаться изменяемой, статически определимой и неизменяемой, наконец, статически неопределимой. В исключительных случаях может оказаться одновременная статическая неопределимость и изменяемость системы. Если шарнирная схема рамы статически неопределима, расчет рамы вообще не может быть доведен до конца без учета деформаций, вызываемых продольными силами.

Изменяемые системы разделяются по степени их изменяемости, то есть по числу связей, к-рое необходимо добавить для превращения изменяемых систем в неизменяемые. Раму, шарнирная схема которой и-кратно изменяема, называют η-ярусной рамой. Шарнирная схема (фигура 5, б) рамы, изображенной на фигуре 5, а,—неизменяема; узлы такой рамы неподвижны, ярусность ее равна нулю. На фигуре 6 и 7 изображены двухъярусные рамы; для превращения их шарнирных схем в неизменяемые достаточно добавить по два стержня, изображенных пунктиром. Рама на фигуре 8 одноярусная, но ее шарнирная схема

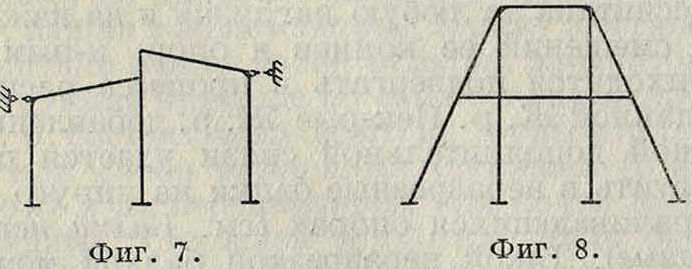
не только изменяема, но и статически неопределима, поэтому при расчете необходимо учесть деформации от продольных сил. Чем выше ярусность рамы, тем менее выгодно выбирать основную систему, состоя щую из однопролетных статически неопределимых балок.

При определении коэффициентов канонических ур-ий следует иметь в виду, что они по абсолютной величине попарно равны друг другу. На основании теорем взаимности

^ik⁼ ^ki г 4 г ~ Xrl ί ^ гг ⁼ Чг · Поэтому достаточно вычислить только половину побочных коэффициентов. Систему канонич. ур-ий (для облегчения решения) можно переписать т. о., чтобы коэфф-ты ее были симметричны. Для этого достаточно изменить знаки во всех членах всех ур-ий, начиная с (?г+1)-го. Коэфф-ты и свободные члены <5, представляющие собой перемещения по направлению неизвестных сил, например Х_{, и вызываемые тоже силами, вычисляются по теореме Мора:

где М_г—изгибающий момент в основной системе, вызываемый силой -Х_г=1; М_к—изгибающий момент в той же системе, соответствующий той нагрузке, которая вызывает

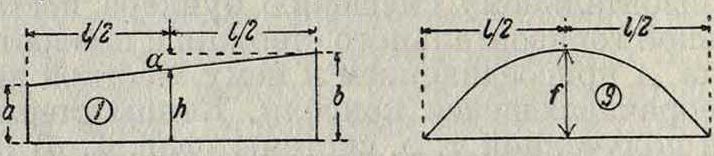
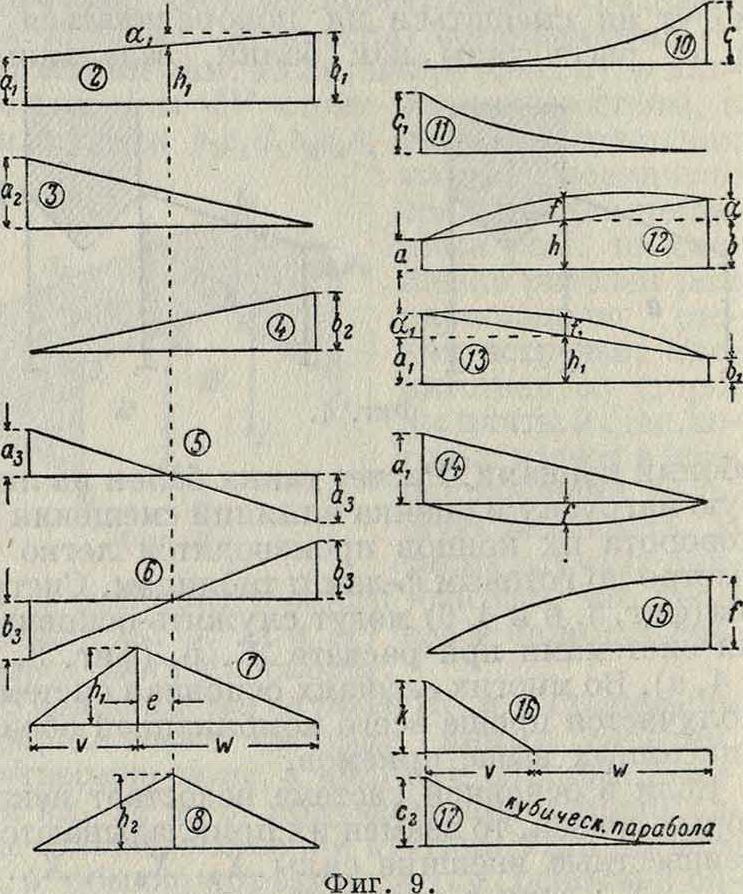
искомое перемещение; EI—жесткость стержней Ж. р. Интеграл берется по всем стержням системы. При вычислении интегралов можно воспользоваться табл. 1; схемы к таблице даны на фигуре 9. Цифры, помещенные в первых двух столбцах, означают номера схем, соответствующих очертанию эпюр М_{и М_к на том стержне, для которого вычисляется интеграл.

Коэффициенты х, представляющие собой усилия, возникающие по направлению неизвестных перемещений (наир. Δ,.) под влиянием перемещений опор основной системы, также м. б. определены по теореме Мора:

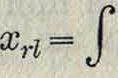
Mr Μι EI

ds,

г	k	J MiMjcds	i	k
1	1	(a*+ab + b*)=l	3	17
1	2	— [a (2а1+Ь1) + Ь (2Ь1+а1)] =	4	7
		= 4 [а,(2а+Ь)+Ь1(2Ь+а)] = b	4	12
		— l (hhi+-(^cti+4h/i1+i>b1)	4	14
1	3	~ (2a+b)	4	15
1	5		4	16
1	6	-T(a-b)	4	17
1	7	y (1 h ~ _t)=~i[a (1++b (1+v *1	5	5
1	8	hh22 1	5	6
1	9	2 fhl 3	5	7
1	10	(3 b+a)	5	10
1	11	~(3a+b)	5	15
1	13	1 (hh‘+ 3 )~g (a«i-rik^+bbO	5	17
1	14	- [aI(2a + b)+4/1h]	7	7
1	15	(b-r3h)=~ (3a+5b)	7	8
1	16	kv 2va Ύ a+~Wj	7	9
1	17	ci(ia+b)	7	10
3	3	lal	7	15
3 3	4 5	la2b2 6 la2a3 6	8 9	9 9
3	6	la2b3 6	9	10
3	7	b. i Ci2 -^a+w)	10	10
3	8	h2a2l	10	11
3	9	fa2l	10	16
3	10	cla2 12	11	16
3	11	cxla2 4	12	12
3	12	~^+2h)	12	13
3	14	0h+f)	12	17
3	15	ajl 4	17	17

f MjMkds

d₂C₂l

5

h,b₂

(l + v)

~‘(b+2h)

— (α,+2/) 5b₂fl 12

kb₂v²

61

b ₂c₂l 20 ajl 3

_ a_sb₃l 3

a_ahj_l

3

la₃c

~6~

_ la₃f 6

3 la₃c₂20 h l ~3~

hjh₂l ^ l 2%v

UK

3

hyC 12

П 2v²

2 31 )

(.+=)

Ы)

¥ (·«-?)

bfh₂l 12 8 f*l 15 cfl

T

c4

5

cC₁l

~W

ckv^z 121² kVCi

Ш²

(6l²-Alv + v²)

I [hh_l+

c₂l I, b 2 Λ τ(^α+4⁺8^)

c‘i_

7

где Μ,.—изгибающий момент в основной системе, соответствующий перемещению A_r= 1; Μι—изгибающий момент в той же системе, соответствующий перемещению Δ_χ, вызывающему усилие х_н. Часто величины х можно найти и проще—непосредственным определением усилий в дополнительных связях основной системы.

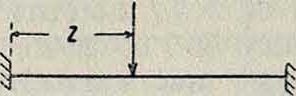
Усилия в связях, вызываемые силами Х_{или заданной нагрузкой, и перемещения по направлению неизвестных сил, соответствующие перемещениям А_г, не м. б. определены по теореме Мора и вычисляются непосредственно — расчетом основной системы. Для балок, заделанных на одном или двух концах, применяемых в основных системах особенно часто, можно воспользоваться данными фигура 10.

Для сосредоточенных грузов и других нагрузок можно воспользоваться линиями влияния опорных моментов. Вычисление ординат линий влияния опорных моментов балки, заделанной двумя концами, можно произвести, пользуясь данными табл. 2. При вычислении ординат линий влияния опорного момента балок, заделанных на одном и опертых на другом конце, можно пользоваться данными табл. 3.

Т. Э. т. VII.

28

Таблица 2.—3 н а ч е н и я ξ, μ^ и μ для балок, заделанных двумя концами.

Таблица 3 .—3 начения I, μ*_Λ. и для балок, заделанных на одном и опертых на другом конце.

^ζ Н

I-i-1

г-I--1 !·-I

/^1 Z. i
I		1
Линия влияния левого опорного момента		Линия влияния правого опорного момента
ъ-Н1	-т)‘=« i-f)!	" 2:2 Λ 2 μη· ~1‘ I1-	)=ί2(ΐ-ί)
-г	К к.	KL
0,00	0,0000	0,0000	1,00
0,01	0,0098	0,0001	0,99
0,02	0,0192	0,0004	0,98
0,03	0,0282	0,0009	0,97
0,04	0,0369	0,0015	0,96
0,05	0,0451	0,0024	0,95
0,06	0,0530	0,0034	0,94
0,07	0,0605	0,0046	0,93
0,08	0,0677	0,0059	0,92
0,09	0,0745	0,0074	0,91
0,10	0,0810	0,0090	0,90
0,11	0,0871	0,0108	0,89
0,12	0,0929	0,0127	0,88
0,13	0,0984	0,0147	0,87
0,14	0,1035	0,0169	0,86
0,15	0,1084	0,0191	0,85
0,16	0,1129	0,0215	0,84
0,17	0,1171	0,0240	0,83
0,18	0,1210	0,0266	0,82
0,19	0,1247	0,0292	0,81
0,20	0,1280	0,0320	0,80
0,21	0,1311	0,0348	0,79
0,22	0,1338	0,0378	0,78
0,23	0,1364	0,0407	0,77
0,24	0,1386	0,0438	0,76
0,25	0,1406	0,0469	0,75
0,26	0,1424	0,0500	0,74
0,27	0,1439	0,0532	0,73
0,28	0,1452	0,0564	0,72
0,29	0,1462	0,0597	0,71
0,30	0,1470	0,0630	0,70
0,31	0,1476	0,0663	0,69
0,32	0,1480	0,0696	0,68
0,33	0,1481	0,0729	0,67
0,34	0,1481	0,0763	0,66
0,35	0,1479	0,0796	0,65
0,36	0,1475	0,0829	0,64
0,37	0,1469	0,0862	0,63
0,38	0,1461	0,0895	0,62
0,39	0,1451	0,0928	0,61
0,40	0,1440	0,0960	0,60
0,41	0,1427	0,0992	0,59
0,42	0,1413	0,1023	0,58
0,43	0,1397	0,1054	0,57
0,44	0,1380	0,1084	0,56
0,45	0,1361	0,1114	0,55
0,46	0,1341	0,1143	0,54
0,47	0,1320	0,1171	0,53
0,48	0,1298	0,1198	0,52
0,49	0,1274	0,1225	0,51
0,50	0,1250	0,1250	0,50
	Кг.	κι	*-τ

Симметричные Ж. р. допускают значительное упрощение решения. Всякую нагрузку, действующую на такую Ж. р., можно разложить на две части: симметричную и обратно симметричную. Пример такого раз

j"— г —		rH
	1 1 -·>	I &
*		,· 1 ·|
ί		ί
Линия влияния опорного момента при заделке на левом конце		Линия влияния опорного момента при заделке на правом конце
, 1 г (		lz	хг
^•=2(1		μ“· = 2 г ν1-’ί 7 =
= §f(1-	-ί) (2-ί)		-«*)
*=т	Кг.	μη.
0,00	0,0000	0,0000	1,00
0,01	0,0099	0,0049	0,99
0,02	0,0194	0,0099	0,98
0,03	0,0287	0,0149	0,97
0,04	0,0376	0,0199	0,96
0,05	0,0463	0,0249	0,95
0,06	0,0547	0,0299	0,94
0,07	0,0628	0,0348	0,93
0,08	0,0707	0,0397	0,92
0,09	0,0782	0,0446	0,91
0,10	0,0855	0.0495	0,90
0,11	0,0925	0,0543	0,89
0,12	0,0993	0,0591	0,88
0,13	0,1057	0,0639	0,87
0,14	0,1119	0,0686	0,86
0,15	0,1179	0,0733	0,85
0,16	0,1236	0,0779	0,84
0,17	0,1291	0,0825	0,83
0,18	0,1343	0,0871	0,82
0,19	0,1393	0,0916	0,81
0,20	0,1440	0,0960	0,80
0,21	0,1485	0,1004	0,79
0,22	0,1527	0,1047	0,78
0,23	0.1567	0,1089	0,77
0,24	0,1605	0,1131	0,76
0,25	0,1640	0,1172	0,75
0,26	0,1674	0,1212	0,74
0,27	0,1705	0,1251	0,73
0,28	0,1734	0,1290	0,72
0,29	0,1760	0,1328	0,71
0,30	0,1785	0,1365	0,70
0,31	0,1807	0,1401	0,69
0,32	0,1828	0,1432	0.68
0,33	0,1846	0,1470	0,67
0,34	0,1863	0,1603	0,66
0,35	0,1877	0,1536	0,65
0,36	0,1889	0,1567	0,64
0,37	0,1900	0,1597	0,63
0,38	0,1908	0,1625	0,62
0,39	0,1915	0,1653	0,61
0,40	0,1920	0,1680	0,60
0,41	0,1923	0,1705	0,59
0,42	0,1924	0,1730	0,58
0,43	0,1924	0,1752	0,57
0,44	0,1922	0,1774	0,56
0,45	0,1918	0,1794	0,55
0,46	0,1913	0,1813	0,54
0,47	0,1905	0,1831	0,53
0,48	0,1897	0,1847	0,52
0,49	0,1887	0,1862	0,51
0,50	0,1875	0,1875	0,50
	Κι.	Кг.	«-1

ложения показан на фигуре 11. Из этого примера видно, что обе частные нагрузки в сумме дают заданную; кроме того, от симме-

тричной нагрузки все явления в Ж. р. будут симметричные, то есть, если, наир., в каком-нибудь сечении происходит растяжение, то и в симметрично расположенном сечении тоже будет растяжение; если какое-нибудь сечение перемещается при деформации по направлению к оси симметрии, то и симметричное сечение перемещается к оси симметрии. При обратно симметричной нагрузке, наоборот, растяжению какого-либо сечения соответствует сжатие в сечении, ему симметричном, перемещению точки к оси симметрии Ж. р.—перемещение от оси симметрии для симметрично расположенной точки. Поэтому для каждой из частичных нагрузок число неизвестных в системе будет значительно меньше, чем при произвольной нагрузке. Если при выбранной уже основной системе общее число неизвестных для решения рамы равно те, то при решении на симметричную нагрузку будет всего р<т неизвестных, а при решении на обратно симметричную нагрузку ж—р неизвестных. Благодаря разложению нагрузок решение системы ж совместных ур-ий заменяется решением двух

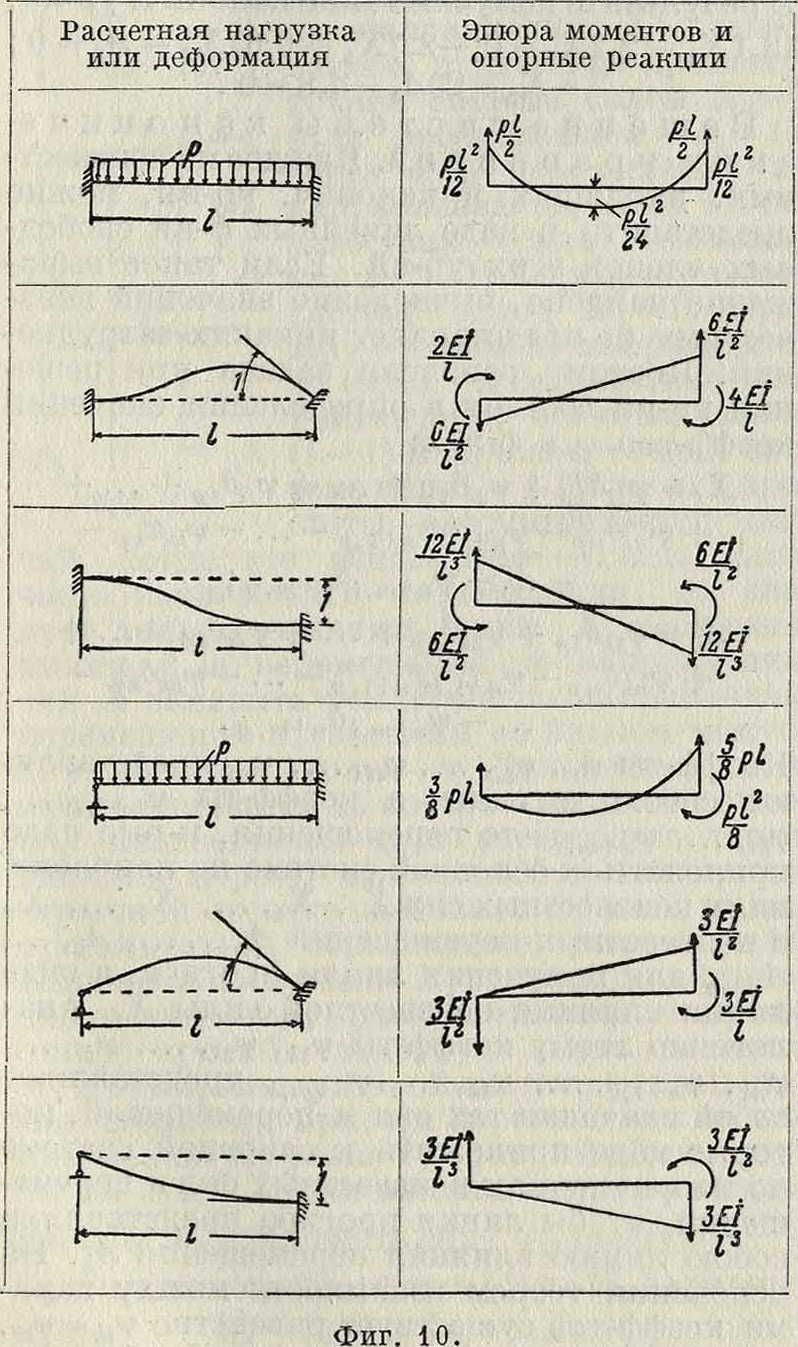
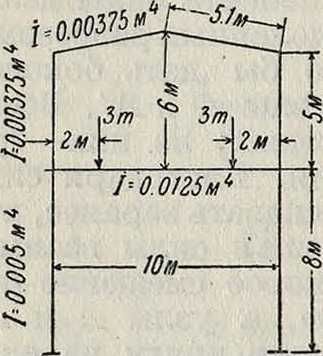
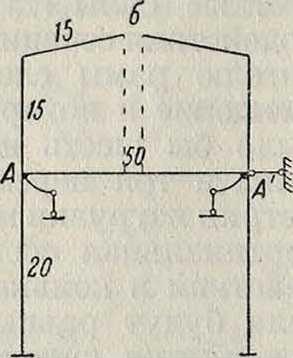
независимых систем ур-ий общим числом те, что значительно проще. Пусть, например, требуется рассчитать Ж. р. (фигура 12,а) на два сосредоточенных груза по 3 тонны Размеры рамы и моменты инерции стержней приведены на чертеже. Для расчета абсолютные значения жесткостей стержней EI не играют

5 т

EI

роли, важно лишь соотношение —ί жест-

Е12

костей стержней. Поэтому жесткости заменены пропорциональными им чи, приведенными на фигуре 12, б. Основную систему удобно выбрать по фигура 12, б, то есть разрезать верхний этаж Ж. р. в коньке, ригель нижнего этажа закрепить от боковых смещений горизонтальными стержнями, а узлы А а А закрепить от поворота. Верхняя часть основной системы статически определима, а нижняя состоит из балок, заделанных обоими концами. При произвольной нагрузке следовало бы в разрезе приложить три неизвестные силы (три компонента силы взаимодействия сечений, разделенных разрезом), ригелю рамы следовало бы дать боковое смещение и повернуть узлы i и!. Всего было бы шесть неизвестных; из. них—три силы и три перемещения. Благодаря симметрии нагрузки можно сказать заранее, что вертикальная составляющая силы взаимодействия в коньке и боковое смещение ригеля будут равны нулю, а узлы А и А повернутся навстречу друг другу на одинаковый угол.

Т. о., остаются всего три неизвестных. Выберем их так: добавим мысленно в месте разреза абсолютно жесткие стержни, опускающиеся до нижнего ригеля, и представим себе, что связь между разделенными разрезом сечениями осуществляется через нижние концы этих стержней. Связь обоих сечений была бы при этом не менее полной. Теперь можно неизвестные силы взаимодействия между частями верхнего этажа приложить к кон- г™ цам жестких стержней. Назовем горизонтальную составляющую силы Х_г, а момент—X,. Третьей _Ып_Ыг5т rfffffffl .*>щ. неизвестной будет 11J ί ПТГ ΊΠΤΤΪΤ

угол поворота узла А, к-рый обозначим через Δ₃ (угол поворота узла А по симметрии имеет ту же величину). При действии на основную систему сил Ij=l и моментов Х₂=1 получаются эпюры моментов, изображенные на фигуре 12,в и

^^ ji При ПОВОрОТО Обратно симметричной чость нагрузки узлов А И А на Фигура и. встречу друг другу на угол Δ_ζ—1 рама получит деформацию, изображенную на фигуре 12,д. Вычислим изгибающие моменты, соответствующие этой деформации. Для ригеля (по таблице опорных моментов балки, заделанной ,двумя концами) находим момент на левой опоре: от поворота левого узла

4ei __ 4-50 _ _9П

I 10 ~ ^м»

от поворота правого узла

2 ΕΙ__2 · 50

i ~ ίο

	Г				500кг/м

Полная нагрузка

Симметричная часть нагрузки

25т ТППТШ^г/»

1т

150кг/м - i_/y77_* 25т

= -ю,

от одновременного поворота узлов

М=+ 10.

Для верха стойки под влиянием его поворота момент равен

iEI _ 4^20 _ _{1 п}.

г ~ в “^iU ’

для нижнего конца стойки

2EI 2-20 _г

Т-=^“=⁵·

По этим значениям моментов построена эпюра фигура 12, д, причем, как и во всех остальных случаях, ординаты эпюры отложены со а

в

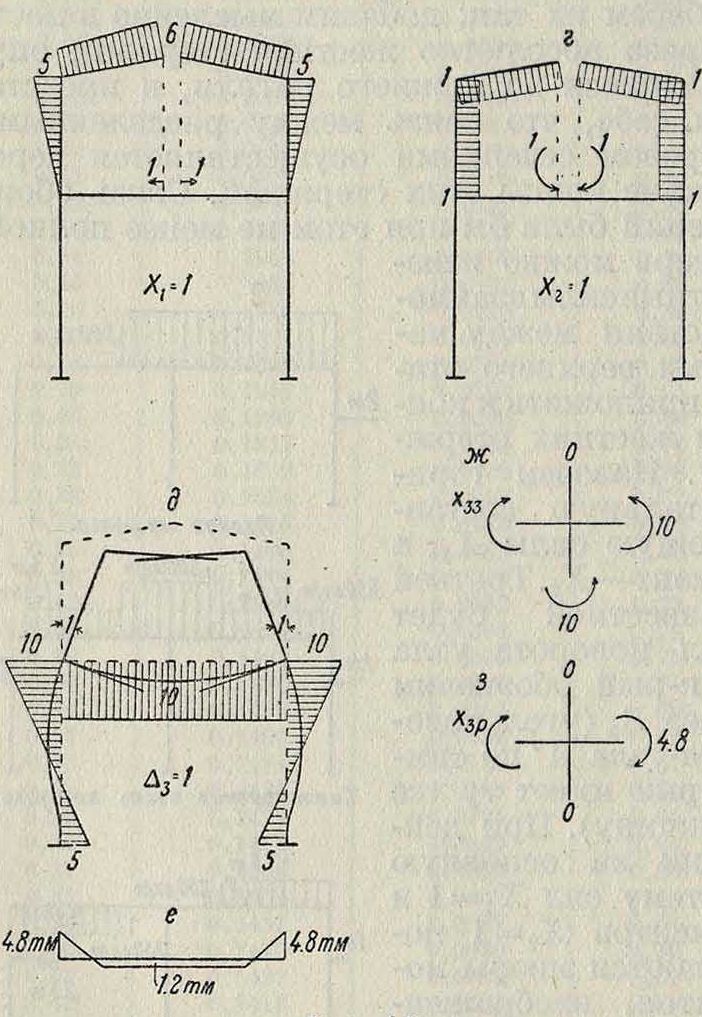
Фигура 12.

стороны растянутого волокна. Построим, наконец, эпюру моментов в основной системе от заданной нагрузки. Благодаря закреплению узлов эпюра занимает только нагруженный стержень. По линиям влияния, для |=0,2 и f=0,8, находим опорный момент: М=- 3 · 10(0,128 + 0,032)=- 4,8 тм. Эпюра показана на фигуре 12,е.

Теперь можно перейти к вычислению коэффициентов и свободных членов ур-ий. Благодаря симметрии можно ограничиться рассмотрением половины Ж. р. Для вычисления перемещения <5_П интегрируем эпюру для Х_{=1; пользуясь таблицей для вычисления интегралов Мора (схемы 1-1 и 3-3), находим:

⁵п=й[(5^гД5-6 + 6*) + ^]=13,1.

Для <5₁₂ интегрируем эпюры Х_к=1 и Х₂=1; по схемам 1-2 и 1-3 находим:

^=-п[-2¹(⁵ + 6) + ^]=-2,7.

Из эпюры для Х₂=1 по схемам 1-1 и 1-1: (5 + 5,1)=0,67.

Для определения момента ж₃₃, развивающегося в закреплении узла А, при его повороте на угол А₃=1, вырежем этот узел (фигура 12, ж) и составим для него уравнение моментов:

ж₃₃=10 + Ю=20.

Коэфф-ты ж₃₁ и ж₃₂ находим аналогично, причем благодаря переносу сил×на концы жестких стержней получается:

ж₃1=<5₁₃=0 и х₃₂=<5₂₃=1 Подобным же образом определяются и свободные члены (фигура 12,з):

^<5ip=0; д_2р=0 и х_зр=+ 4,8.

В результате получим такие канонич. ур-ия: 13,12^ - 2,7Х₂=0; -2,7.x,. + 0,67Х₂ - А₃=0 ;

—Х₂ — 20А₃ — 4,8=0.

Решение системы канонических уравнений. Каждое из неизвестных, входящих в канонич. ур-ия, можно представить в виде линейных ф-ий свободных членов этих ур-ий. Если такое выражение найдено, вычисление значений неизвестных не представляет никаких затруднений. Поэтому основная задача при решении ур-ий состоит в определении значений коэффициентов ψ в ф-лах:

Χϊ — ^ΊΡ /Ρ ρ Д Ψ2Ρ2р Д *.·· Д ΨίΡΐρ д * · д

Д ΨηΡηρ ^ΊΡη+1,Αη+1₁ρ *·· ^РкР^кр ··· Ψη+νη,Рп+т,р >

А=ΨιΑρ Д УгАр Д · · · Д УгАр Д · · · Д

Д ΨηίΡηρ Ψη+λ,1$η+1,ρ ” ··· УкРкр

· · · Ψ п+т,1р п+т,р ·

Коэфф-ты ψ_Η, ψ_2ί, ., у>_и,., v>ni представляют собою те силы, а коэфф-ты ψ_{η+1 ti}, ., %(·,.·, Ψη+m.i—^те перемещения, которые надо приложить к основной системе по направлениям неизвестных сил Х_1; Х₂, ·, X», ···, Х_пи неизвестных перемещений А_п+1,., А_к, ., А_п+т для получения линии прогиба, в виде линии влияния неизвестной силы Х_г. Аналогично этому коэфф-ты у_л, у>_2к,., Wn, ., Ч’пк, Ψη+1,1с,···, У».···. Ч’п+т,к представляют собой значения тех сил и перемещений, которые надо приложить к основной системе по направлениям неизвестных сил и перемещений, чтобы линия прогиба представляла собою линию влияния перемещения А_к. На основании теорем взаимности между парами коэффициентов существует равенство ψ^=Ψη· Равенство это справедливо, когда обе неизвестные величины с индексами i,к—силы, когда эти неизвестные—перемещения, а также когда одна из неизвестных—сила, другая—перемещение. Для нахождения величин ψ рекомендуется следующий путь: переход от основной системы к заданной Ж. р. совершается постепенно путем изучения ря-

Λ

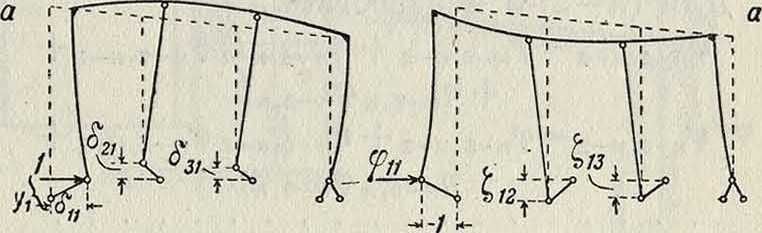
да промежуточных систем. Первая промежуточная система получается из основной введением первой неизвестной: если первая неизвестная — сила, то вводится первая связь, если это—перемещение, то выбрасывается соответствующая связь. Подобно этому введением, кроме первой, еще и второй неизвестной получается вторая промежуточная система, затем третья и т. д. Если число неизвестных равно п + т, то последней промежуточной системой является (п + + т — 1)-я; с введением последней неизвестной получается заданная НС. р. Так, если при расчете Ж. р. (фигура 13, а) принята основная система по фигура 13, б, то промежуточных систем будет всего две (фигура 13, в и 13, г).

Обозначим далее: через ζ_α·—усилие в последней из введенных связей (или перемещение по направлению последней из выброшенных связей) в г-й промежуточной системе, вызываемое силой Х_к=1 (или J перемещением А_к= 1, если к-я неизвестная — перемещение); через η_Ά — усилие по направлению Х₍ (или перемещение по направлению A_f), вызываемое в (к—1)-й промежуточной системе силой Х_к=1 (или перемещением А_к=1); через бг(г)—перемещение по направлению Х₍ (если г-я не-^ ^ известная — сила), вызывае-

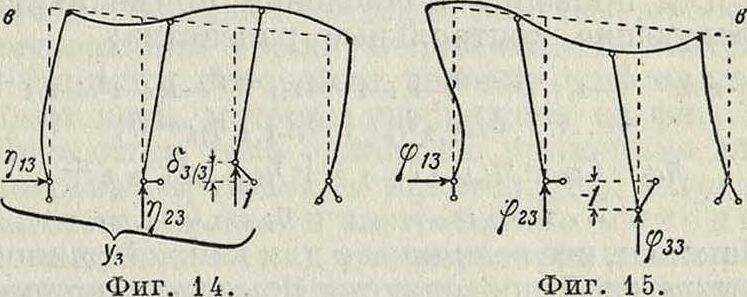
Л Л мое в (г — 1)-й промежуточной системе силой Х_{== 1; через х%(г)—усилие по направлению (если г-я неизвестная—перемещение), возникающее в Л Г* Л (г — 1)-й промежуточной системе при /1_г= 1. Ниже для простоты рассматривается случай, когда все неизвестные — силы. Если часть неизвестных—перемещения, то следует только заменить силы×перемещениями Δ, а перемещения по направлению сил×заменить усилиями по направлению перемещений Δ, взятыми со знаком минус, то есть вместо δ писать—ж. Дальнейшее изложение опирается на построении линий влияния неизвестных. Для построения линии влияния первой неизвестной в 1-й промежуточной системе следовало бы дать по направлению Х_х перемещение, равное ( — 1). Если по направлению .Xj приложить в основной системе силу, равную единице, получим линию прогиба, подобную линии влияния Х_х в 1-й промежуточной системе, (модель линии влияния), причем перемещение по направлению Х_г равно й₁₁(фигура 14). Для получения самой линии влияния надо по направлению Х_х приложить силу φ_1χ равную — — ·

Фигура 13.

Ординаты линий влияния (фигура 15, а) равны:

£l2 ⁼ Φΐβΐΐ ’> £l3 ⁼ Ψΐβζΐ >

(в общем случае ζ_1ι=ψ_ηδ_α, ., ζ_1η=·=φ_1χ δ_η1). Зная влияние всех сил×на усилие в 1-й связи 1-й промежуточной системы, можно перейти ко 2-й промежуточной системе. Сила Х₂=1, приложенная к 1-й промежуточной системе, вызывает в 1-й связи этой системы усилие ?;₁₂=ζ ₁₂. Реакцию 1-го стержня можно заменить внешней силой

??₁₂ и рассматривать совокупность двух сил— силы, равной 1 и действующей по направлению Х_г, и силы, равной %₂ и действующей по направлению Х_х—как группу сил или обобщенную силу У₂=1, действующую на основную систему (фигура 14). Тогда

<?2(2)=1 · <5₂₂ + ??₁₂<5₂₁ ·

Чтобы получить линию влияния Х₂ во 2-й промежуточной системе, надо приложить вместо У₂=1 группу Ф₂, состоящую из сил

Фи ^{= —} и Фи — ~~ ЯиФю

Отсюда (фигура 15, б)

£23 ⁼ Φ%β32“Ь Фи^ЗИ

и в общем случае еще

£24 — Фз2р42 + Φΐβ&1>

£2п ⁼ Φϊβηΐ "Ь Ψι-β,Λ ·

Под влиянием силы Х₃=1, действующей на 2-ю промежуточную систему, в стержне 2-м возникает усилие >?₂₃=£₂₃, а в стержне 1-м—· усилие

Via ~ 1 £l3 У *?2з£12 ·

Совокупность сил 1, г _гъ и η₁₃ рассматривается как группа У₃=1, действующая на основную систему. Масштаб модели линии

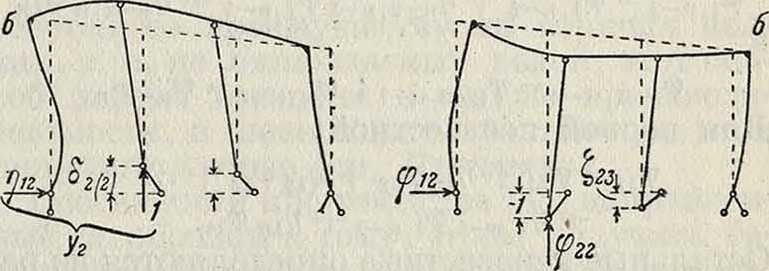
влияния силы Х._л в 3-й промежуточной системе, то есть перемещение <5₃(₃) определяется по формуле:

^з(з) ⁼ ^33 У ^23^32 У ^13^31*

В общем случае, переходя т. о. от одной промежуточной системы к другой, находят, наконец, силы ψ для последней неизвестной Х_п уже в заданной Ж. р.:

Ψηη - Фпп - _δη(η) >

Ψη—Ι,η ⁼ Φη—Ι,η ⁼ Vn—Ι,ητηη)

Ψ2 П ⁼ *Р2П ⁼ *l2n^fPnn’

Win ⁼ Win ⁼ VlnWnn·

Линии влияния для сил×в промежуточных системах представляют собой в то же время линии влияния групп Y в основной системе. Между силами X, действующими на основную систему, и группами существует простая зависимость (фигура 14):

Ύ —Ύ

Άΐ—1 ^ 11—1 + Vn—Ι,η А» 1

Άϊ—2 Аг— 2 ~П Vll—2,«—1 1 п—1 ~Ь Vll—2,η Аг 1

Ά — А + Ί23 А + Ί2Ι А + · · · +

“Ь V 2, ϊΐ—1 Al—1 “Г Vin Аг i А=А + Ίΐ2 А + Ίΐ3 A + ··· +

+ ’ll,»-! Аг-ι + ’ll» Аг·

Для случая фигура 14 и 15 следует подставить №=3.

На основании этих ф-л, для вычисления величин у>, относящихся к (те—1)-й неизвестной, следует к величинам _t прибавить величины <p_ni Пп-ι,η

Ψη—ι,η—l ⁼ Φη—ι,η—ι ~Ь V11-1,11 Фп—1,11 1

Ψ 11—2,»—1 ν’»—2,11—1 "T Vn—Ι,ηΨη—2,111

Ψζ,η—1 Ρ‘ί,Ιί—1 “Ь V11-1,П Ψ2ni

Ψι,η—ι ν’ 1,ιι—1 Φ" Vn—1,11 Ψΐη.

Кроме того, Ψη,η-ι^Ψη-ι,η·

Для (те—2)-й неизвестной:

V 11-2,11-2 ⁼ Ψη—2,11—2 Г Vll—2,11-1 Ψ11-2,11-1 ~Т + Чц—2,П ^fPn—2,111

ΨΐΙ—3,11—2 ~ ν’»—3,11—2 4 " Vn—2,П—1 ΨΐΙ—3,»— 1 “Γ !” Vll—2,11 Ψη—3,111

Ψ2,11-2 ⁽Ρ2,11—2 “Ь V11—2,11—1 Ψζ,ιι—1 Φ" Vn—2,η Ψ2η

Ψ 1,11—2 Ψΐ,η—2 Φ" Vn—2,11—1 Ψί,η—1 Φ V11—2,11 Ψΐη И

ν’ 11—1,η—2 - Ψ η—2,11—1 1 ΨΐΙ,ΙΙ—2 ⁼ Ψ 11—2,11.

Для первой неизвестной:

V4i=Ψιι + Ίι₂ Vis + Ί13 V13 + · · · +

Vl,n—1 ^rP 1,11-1 + Vlll Ψΐη.

Остальные неизвестные определяются из равенства у>_{1=у>_и.

Для проверки вычислений применяются следующие контрольные равенства:

^i-lii)=&i—i,i 1 ΦΑ-Ι,ί-ΐΊί-Ι,Α~^i-l,i-2Vi-2,i +

+ ·· +^·-ι,2’?2,: + <⁵ί·-ι₎ιΊιί=0;

Vile=Cik + Vi,к-1 £fc-l,k + Vi,lc-2 £b-t,k +

^г,г+2 Сг- -2,к H" 1 Ci+l,Jc ·

Наконец, все величины ψ для каждой данной неизвестной проверяются помощью системы равенств:

ViAi+VsAsf ··· +v»-i,A,«-i+v«ili*=0;

Vi Ai + V>2 Аг + · · · + Ψη-1, А, η—ι + V» А»=0;

ViAi + % Ai + · · + %-i,i di,ii-i + Ψηί δ in=1 ί

Wlfinl+ Ψ 21^112 + + Ψη-1, Αϊ,«-1+ ΨηΦηη^ 0.

Лит.: Стрелецкий Η. С., К расчету сложных статически неопределимых систем, М., 1922;

Самойлов Л. А., Основы расчета рам, «Труды Моек, ин-та инш. транспорта», М., 1927, вып. 3; его же, Расчет рам по методу фокусов, там же; Гвоздев А. А., Расчет статически неопределимых систем, М., 1927; Жемочкин Б. Н., Расчет статически неопределимых систем. Способ угловых деформаций, М., 1927; Бейер К., Статика железобетон. сооружений, пер. с нем., М., 1928; Mohr О., Abhandlungen ausd. Gebiete d. techn. Meelianik, p. 489,

2 Auflage, Berlin, 1914; Pirlet J., Kompendium d. Statik d. Baukonstruktionen, B. 2, T. 1, Berlin, 1921; S u t e г E., Die Methode d. Festpunkte, Berlin, 1923; G e h 1 e г W., Der Rahmen, Berlin, 1926; Osten-f e 1 d A., Die Deformationsmethode, B., 1926; Pasternak P., Berechnung vielfach statisch-unbestimm-ter biegefester Stab- u. Flachenlragwerke, В. 1, Zurich, 1927: Mann L., Theorie d. Rahmenwerke, auf neuer Grundlage, B., 1927. А. Гвоздев.