> Техника, страница 47 > Замкнутая антенна

Замкнутая антенна

Замкнутая антенна, антенна (смотрите), состоящая из одного или большего числа полных витков провода. К категории 3. а., понимаемой в широком смысле как противопоставление классу открытых антенн, относятся: 3. а. в собственном смысле этого термина, рамки (смотрите), гониометрии, антенны замкнутого типа (смотрите Гониометр), волновая антенна (смотрите), контурные пеленгаторы (смотрите Пеленгаторы) и нек-рые другие. 3. а., в узком смысле слова (контурная антенна), противополагаемая рамке (рамочной антенне), характеризуется одним или очень малым числом витков, большой площадью каждого витка; кроме того, она обычно подвешивается к той или иной сетевой опоре или опорам, тогда как рамка, представляя собою большое число витков с малой площадью каждого, делается обыкновенно передвижной и поворотной и устанавливается внутри здания. В дальнейшем под 3. а. разумеется частный случай контурной антенны, т. к. все остальные виды описываются отдельно. В современной радиотехнике все виды 3. а., кроме волновой, применяются для целей радиоприема и радиопередачи; особенности излучения и приема при помощи замкнутых форм по сравнению с открытыми см. Излучение и прием.

Характерной особенностью всей категории 3. а. является резкое по сравнению с открытой антенной направленное действие. Поэтому преимущественное применение 3. а. находят в пеленгаторах и приемных устройствах, использующих направленность для целей многократного или избирательного (чтобы избавиться от помех) радиоприема, в радиомаяках и некоторых других передающих устройствах, предназначенных для посылки энергии в определенном направлении. В то время как для приема 3. а. применяются на всем диапазоне волн, используемом современной радиотехникой (от единиц м до десятков тыс. м), излучение при помощи 3. а. практически известно покалишь в диапазоне средних волн (-100-М 500 м).

Параметры одновитковой З.а. Основным, отправным при расчетах 3. а., параметром является коэфф. самоиндукции (далее упрощенно «самоиндукция»); для одновитковых фигур эта величина определяется по формуле

L=(lnf-p + ztS),

где I—периметр виткам—его площадь, г—

радиус поперечного сечения провода, μ— магнитная проницаемость; величина δ учитывает магнитный поток внутри провода и находится по кривой фигура 1; по оси абсцисс отложено значение х=0,281 г уу, где /—

частота, о—удельное сопротивление провода в μ-Ω/cjH³; для медного провода при 20°

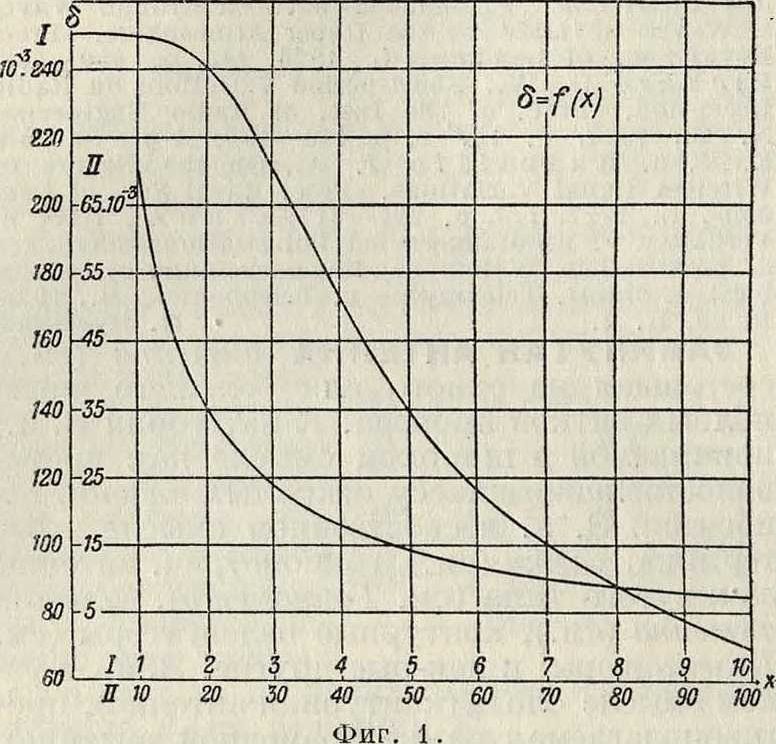
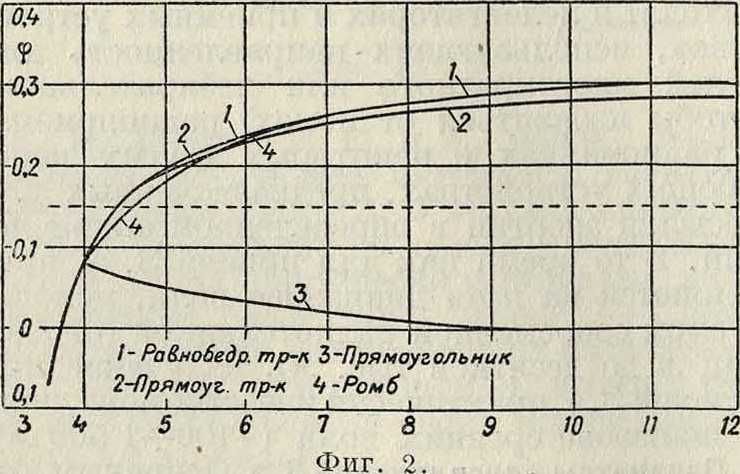
x=0,214rj//; здесь все величины, как и в дальнейшем при расчетах L и С, должен быть выражены в см. Значение ψ для приближенных подсчетов м. б. принято равным 0,15; для точных расчетов следует φ выбирать по кривой фигура 2, на которой представлены аналитически найденные величины φ для правильных фигур, равнобедренного и прямоугольного треугольников, прямоугольника и ром-

оа; величина ψ зависит от отношения —.-;ес-

i/s

ли форма замкнутой антенны не соответствует названным выше фигурам, то приближенно 99=0,15.

Волновой коэфф-т одновитковой 3. а. ) —отношение собственной длины волны к периметру—равен в среднем 2,3. Учитывая все трудности, возникающие при точном расчете емкости антенны вообще [V], а

(*-$)

замкнутых—властности, представляется рациональным использовать уже найденную формулу для L₀ (статической самоиндукции) для нахождения величины статической емкости С₀ такой замкнутой антенны. Из ф-лы Д₀=4|/L₀C₀ легко получается, с уче том λ„

2,3 Ϊ, для замкнутой антенны о,ш

Со =

(ΐη^_Γ-_{φ + μ}ή

Вопрос о сопротивлении току радиочастоты 3. а. остается недостаточно исследованным; для треугольных 3. а., подвешенных к мачтам около 20—30 м, оно порядка 10—15 Ω (при достаточном удлинении собственной волны: is 24-31.

^ло

Параметры многовитасвых 3. а. Теория излучения и приема для многовитковых 3. а. остается приблизительно той нее, что и для одновитковой 3. а. 11а-раметрымноговитковых 3. а. выражаются б. или м. сложными ф-иями от параметров для одно-

OfV

liSJ

Vie


V V V V3	Уа,? о,& ця ifl 1
о.Ьг аЬз оХнйй$А	18CUJ7 008 0Д9 О.! Л
А

Л

Фигура 3.

Фнг. 4.

витковых 3. а.; расчет их еще недостаточно разработан. Приближенно можно считать, что

h/i. =

2 7iS{n

d.,n= —= ^hd.,i · ⁿ, где Sx—площадь одного витка, а n—число витков 3. а.

Самоиндукция и-витковой 3. а. не может находиться по формуле Нагаока (смотрите Катушки самоиндукции), так как последняя действительна только для многовитковых катушек, обладающих малой площадью, с витками, плотно прилегающими друг к другу. Для п < 6 рекомендуется 3. а. приводить к равновеликому квадрату с тем же числом витков и пользоваться далее ф-лой:

L=8tm²(ln I + 0,726 + 0,223 - 8ап(А + В),

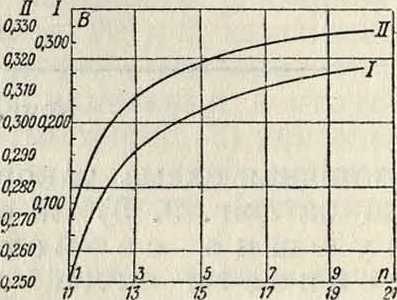
где а—сторона эквивалентного квадрата в см, Ь—осевая длина 3. а. в сантиметров (кратчайшее расстояние между плоскостями первого и последнего витка); А я В находятся по кривым в функции от J (фигура 3)

и п (фигура 4).

Для 3. а. с и>6 с точностью до 10% справедлива ф-ла, данная Эзау для рамок:

L=8an [(in “ - 0,524) + (п - 1) In “ - 0,774].

Емкость (эквивалентная) 3. а. при многих витках приближенно м. б. определена по эмпирич. формуле Эзау: С_э. =al, причем коэфф. а находится в ф-ии от числа витков п по кривой (фигура 5); I— периметр всей 3. а. о,os

Волновой коэффи- _ofi4циент 3. а. к, теоретически равный 2, для многовитковых 3. а., по измерениям В. И. Баженова над 3. а. разнообрази, формы, подвешенными на мачте высотой 60 м, причем нижняя часть 3. а. находилась на высоте 4,5—7 метров над

О 12 34 56789 Ю 15

Фигура 5.

поверхностью земли, равен 2,7—3,5; расстояния между витками были~0,5 л. Из тех же измерений над 3. а. получены след, значения погонной эквивалентной емкости С_э=а:

Число витков. 1 2 4 6

а для 3. а. (по измер.

В. Баженова). 0,01575 0,0108 0,0231 0,0359

а для рамок(по формуле эзау).. 0,00775 0,018 0,0322 0,04175

Отсюда видно, что 3. а. обладают некоторыми преимуществами по сравнению с рамками, т. к. первые имеют меньшую величину эквивалентной емкости.

Сопротивление 3. а. трудно подсчитать; измерения В. Баженова с 3. а., подвешенными на мачте 10—12 метров (при у=3) при расстоянии нижних частей антенны 1-^1,5 метров от земли, дали значения R току радиочастоты порядка 3 Si, в то время как сопротивление того же провода постоянному току определялось величиной!),3£1.Мени приводит величины 10 — 15 Ω для треугольной 3. а. с высотой и основанием порядка 25 метров Ф-ла для полного нагрузочного сопротивления 3. а. может быть представлена в форме R=R_a_ + R_d_ + R^,

гдеЛ_а,— активн. сопротивление току радиочастоты, R_a_—сопротивление диэлектрич. потерь, R_fi —сопротивление потерь на токи Фуко, индукцию в окружающих проводниках, полупроводниках и т. д. В зависимости от длины волны полное сопротивление 3. а. может быть выражено [⁴] ф-лой:

‘i» ’*

R-А-V^λ

где А и В—нек-рые постоянные, численные значения которых зависят от индивидуальных внутренних и внешних свойств контура; формула лишь характеризует закон изменения.

Излучение 3. а. Напряженность поля, создаваемая 3. а. в какой-либо точке пространства, может быть вычислена как сумма напряженностей полей, создаваемых в этой точке отдельными элементами антенны (для упрощения предполагается, что рабочая длина волны 3. а. велика по сравнению с ее размерами и ток квазистационарен). Пусть геометрическая форма 3. а. задана ур-ием y—f (ж); если плоскость 3. а. совпадает с плоскостью XY, а направление, соединяющее р антенну с достаточно >· удаленной исследуемой точкой пространства, лежит в плоскости XZ и составляет с осью×угол φ, то, полагая каждый элемент периметра 3. а. эквивалентным диполю, найдем, что напряженность электрического поля, производимая элементом с координатами (ж, у, 0) в рассматриваемой точке пространства, среднее расстояние которой от антенны равно d, равняется

dE =⁶⁰^ sin

)

/2Tzd 2nt 2πχ COS φ

ΓΓ+ τ

Принимая во внимание, что при квазкста-ционарном токе

2.-ИС COS φ 2пх COS f 2nx COS Ψ

COS —j—=1 и sin-τ · —_λ,

напряженность поля всей замкнутой антен ны, которая создается в рассматриваемой точке пространства, определится как

n=/dH=/^[sm(²f+f)d2 +

. (2nd. 2nt 2ηχ

+ ^cos(— + -Τ·) —

2ηχ COS φ

при чем интеграл должен быть взят по замкнутой кривой, представляют, очертание антенны. Результатом интегрирования является ф-ла:

тп 607il 2nS (2nd. 2nt

^Е=~Ы Г ^C0S9? ^cospr + ~r) ’ где S—площадь замкнутой антенны.

Исходя из тех же представлений об элек-трич. свойствах земли, какие принимаются при расчете напряженности поля открытой антенны, должно учесть поле, создаваемое

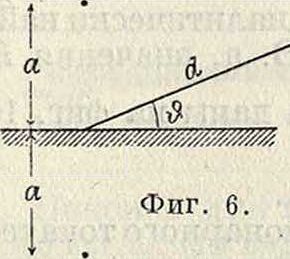
лучами, отраженными от земной поверхности (поле зеркального изображения). Тогда для любой точки Р пространства (фигура 6, где а—высота подвеса 3.а.), направление на которую составляет с поверхностью земли угол # и с плоскостью обеих 3. а. угол φ, напряженность ноля обеих антенн будет тл 60п! · 2nS COS φ (2nd 2nt

-1ы-^cos It + τ +

2na sin & cos <f>

τ-, 60nl · 2nS cos φ

---_ш-cos

(2nd, 2nt

W ⁺ ~Y

2na sin # cos φ j- ) ’

что в результате суммирования дает (если предположить в виду квазистационарности йла sin 9 cos φ ₁,.

COS-j-----= 1):

π r-τ, 77T 120πΐ 2nS (2nd, 2nt

E=Б?! + E₂=---_r cos ψ cos + -y-J ·

Излучение с открытой заземленной антенны характеризуется формулой идеальной радиопередачи:

Е-

120я1Щ.

sin

/2nd, 2nt

~ ~^~τ) ‘

v " P.d "^ΛΧΧ λ ¹ T J

где 1—действующая сила тока в пучности

Т. 9. m. VIII.

антенны. Из сравнения двух последних формул получаем:

к 2nS

К.=— COS φ.

В этом выражении множитель cos φ характеризует направленное действие (смотрите ниже). Для направления наилучшего излучения

следнее выражение представить в виде. й_а.=

= ^г(^ ^, причем ~=К будет коэфф-том

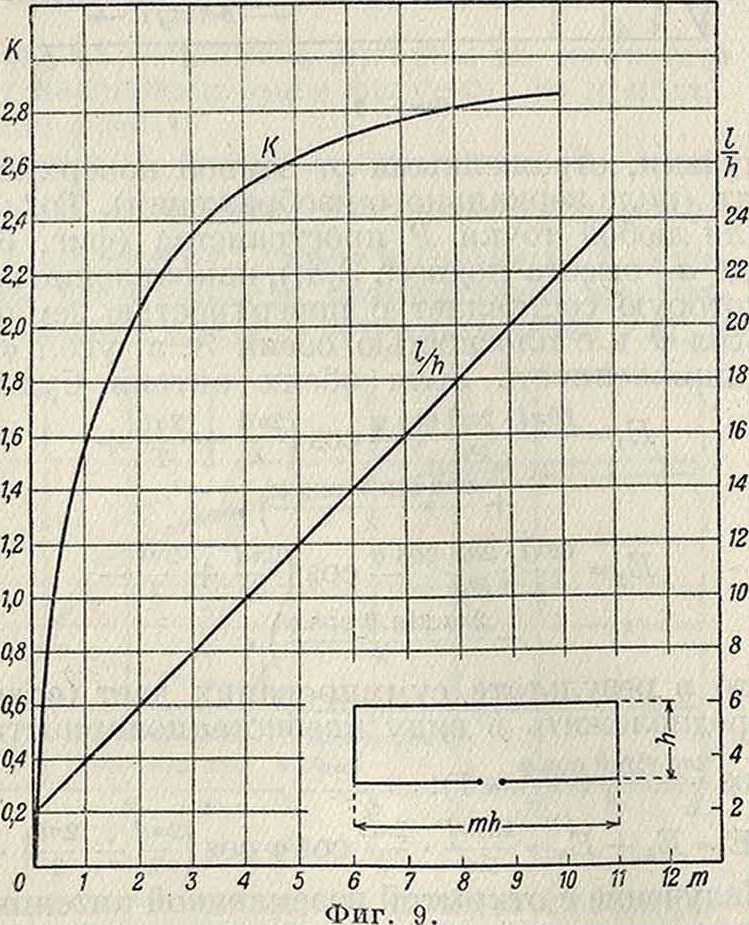
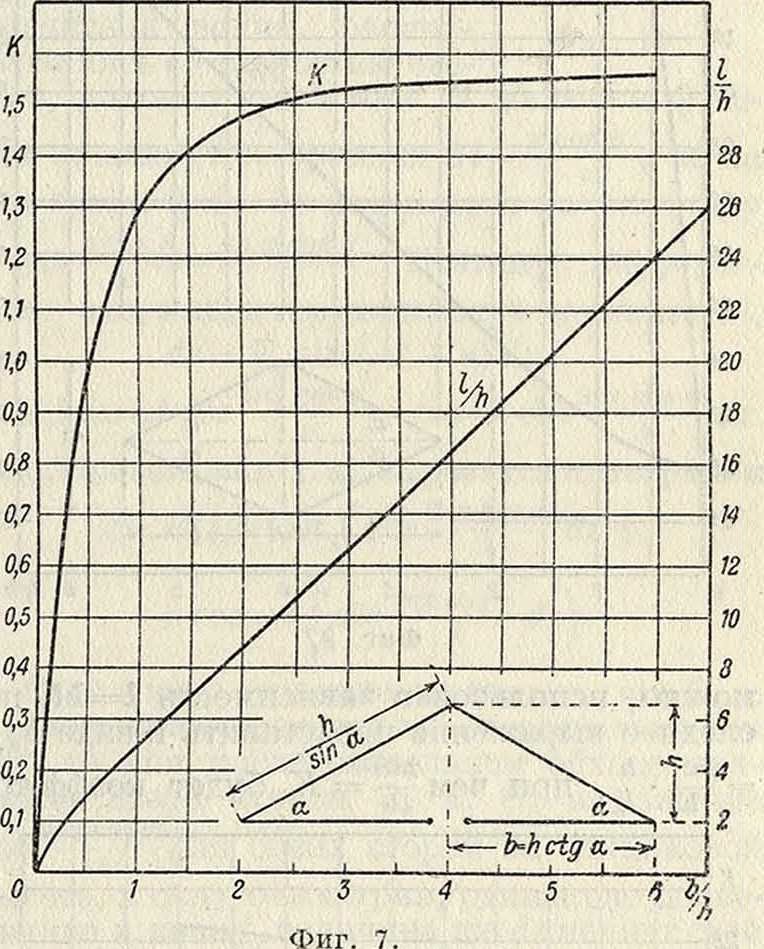
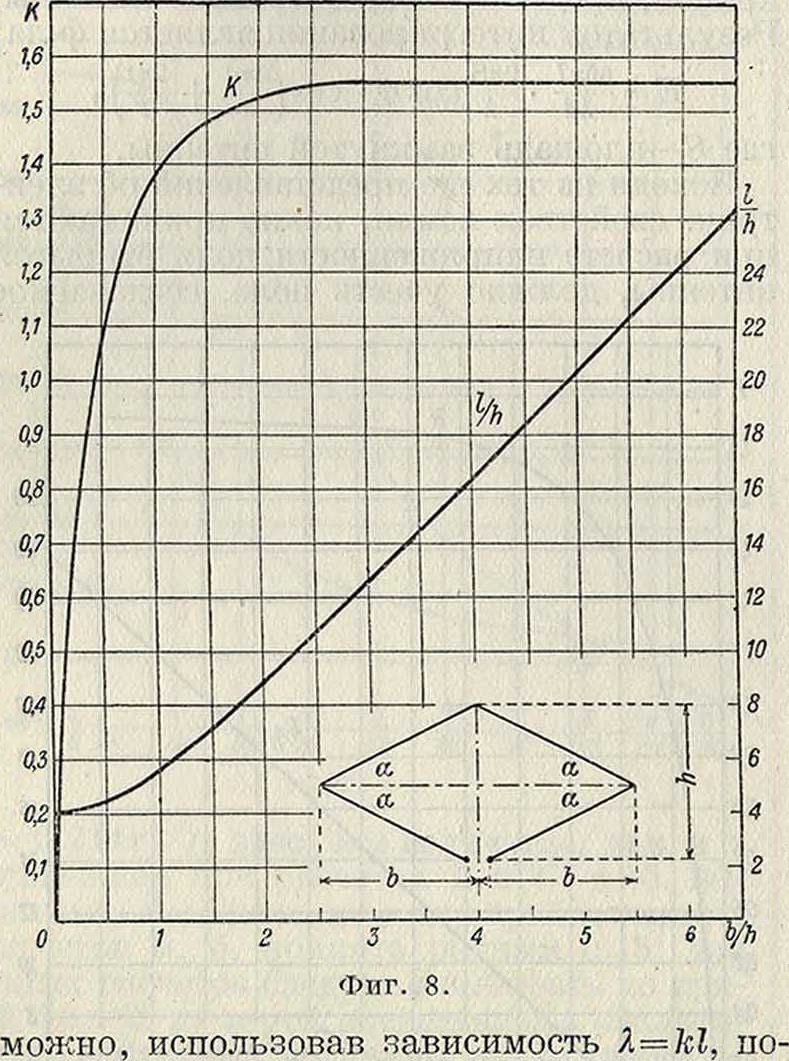
использования геометрия. величины 3. а.; его значения для простейших возможных форм осуществления замкнутой антенны сведены в таблице 1 и представлены на фигуре 7—9.

Таблица 1.— Зависимость К от формы фигу р ы.

Форма фигуры	Значение К	Примечания
Окружность.	1,57
Равнобедренный тр-к.		а — угол при
	. о. ctg_¥	основании
	. о. ctg_¥	треугольника
Ромб..	п --COSа	2а — острый угол ромба
Прямоугольник.	π	т—отноше-
	1+— ш	ние сторон

Для важной в практич. отношении пятиугольной формы 3. а. наибольшее значение К дает положение срезающей линии, перпендикулярное биссектрисе угла при основании

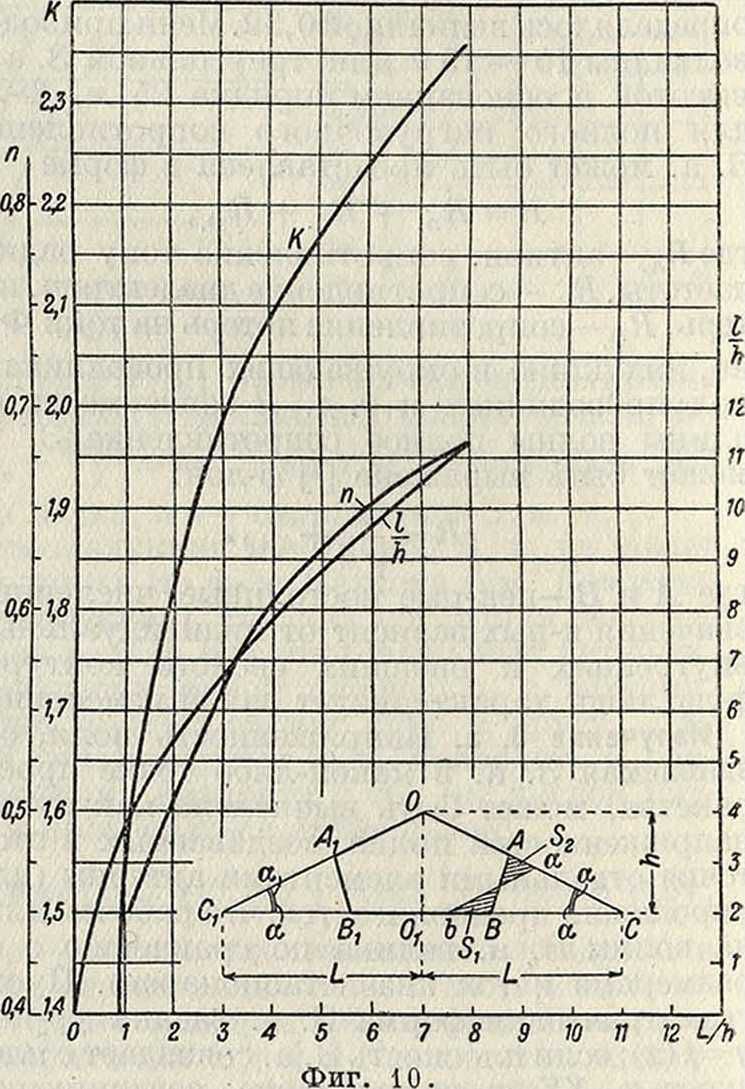
срезаемого треугольника. Аналитически найденные при такой форме 3. а. значения К

ПС

и наивыгоднейшего п=-_Q-^ даны на фигуре 10 для различных ~.

Для случая неквазистационарного тока теория [³] дает суммарную напряженность поля в точке на расстоянии^.d:

E=—g- sin —_λ cos -у cos а

COS φ j COS (yy + -f) +

+ Sin²^ Sin a · COS (Ψ COS φ) Sin + «)].

Та же теория дает для частного случая распределения тока в замкнутей антенне, имеющей форму равнобедренного треугольника, по закону косинуса, следующую формулу:

h;,=h

2 k

2 ft

Hi)

Вводя обозначения:

2ft

= /(fc), получаем

2ft

Hi)

-/(* l).

где

f(i)’

fci=к (^J ; отсюда

*i.=* [/№)-/№>].

Ф-ия /(7c) представлена на фигуре 11 и в соединении с только что выведенной ф-лой позволяет легко рассчитать 7i_a. любой 3. а., выполненной в виде наиболее распространенной формы (для передачи и приема)—равнобедренного тр-ка. Те же выводы получаются

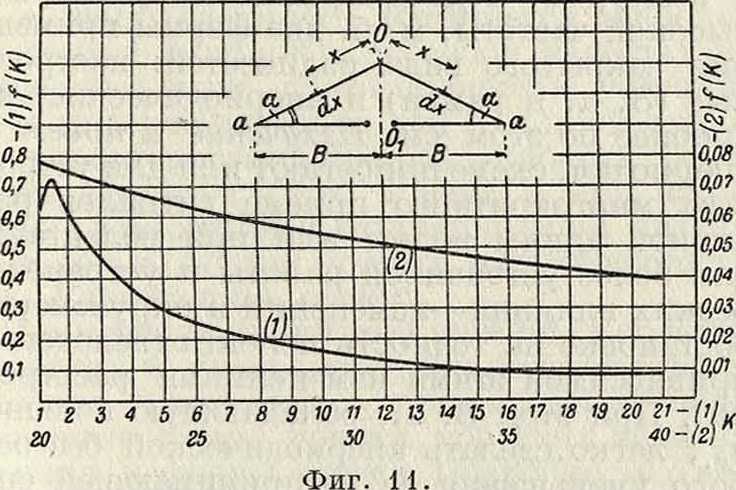
для неквазистационарного тока в случае форм замкнутой антенны — ромбической, прямоугольной и пятиугольной, см. [³]. Некоторое сравнение трех форм замкнутой антенны дает табл. 2.

Таблица 2.—3 ависимостьйа. от! и ft для разных фигур.

Форма фигуры	Максимально возможные
Форма фигуры	hd. I	h(). h
Равнобедренный тр-к	0,118	0,732
Ромб..	0,131	0,5
Прямоугольник.	0,132δ	1

Наконец, для пятиугольной симметричной относительно вертикальной оси 3. а., также имеющей большое практич. значение, полу-1о чается аналогичным пу тем сложная ф-ла, которая с достаточной точностью м. б. представлена в большинстве случаев выражением

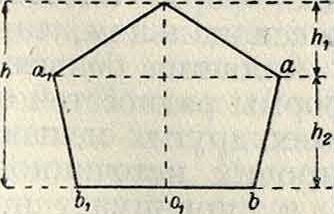
hd.=hd.i + ^а.2 > ^гД^е Кл ^есть действующая высота треугольника, которая находится по предыдущему, а h_d_ г — действующая высота трапеции. Последняя рассчитывается по формуле:

Фигура 12.

^а.2=Тг₂ · 2 cos |д (x₁ -f- ж₂)|sin У-,

где т—средняя линия трапеции; ж₁=оα==0%; х_г=оа + аЬ=оа_г + α₁6_ι (фигура 12).

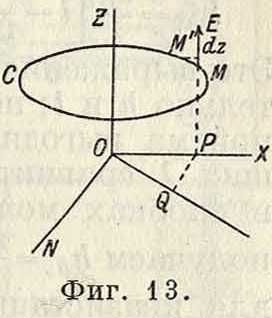
Прием 3. а. Величина эдс при приеме на 3. а. любой формы в зависимости от напряженности поля определяется следующим образом. Пусть 3. а. произвольной формы расположена в плоскости ΖΟΧ (фигура 13), составляющей угол φ с направлением 0Q распространения электромагнитной волны, воспринимаемой рассматриваемой 3. а. Тогда в элементе З.а. dl=MM индуктируется эдс de=E dz, где £7=B₀sina)i; электромагнитная волна, распространяясь со скоростью света с доходит от точки О до точки Q через промежуток времени Δ ί=^хс™ ^ψ, и за это время фаза ее изменяется на величину

X COS φ 2 π χ cos φ -η- ,

^ω —с— ⁼-λ— * Поэтому дифферен-

циал эдс, индуктирующейся в элементе dl, de=Е₀ sin (ωί + a) dz —

= EJsm coi cos —j---1- cos coi sin--~- dz.

Эдс, наводимая в 3. а., выразится интеграл ом е=Е₀ (sin ωί J* cos °^{os φ} dz +

^v i

+ cos coi J sm —— dzj ·

Если в виде ограничения считать, что З.а. расположена симметрично относительно оси 0Z, то при последовательном обходе правой и левой сторон 3. a. (i) выражение 2пх cos φ gr „

cos—д—для обеих сторон на одинаковой высоте, в силу симметрии, одинаково по величине и знаку, величина же dz меняет свой знак. Тогда первый интеграл обращается в нуль, и при указанном ограничении получается соотношение:

е=Е_а cos coi sin ~^πχ ™-^{s φ} dz.

Амплитуда этого выражения равна E_Mr=E₀S sin ²--f^ _dgm

Если очертание 3. а. задано ур-ием ж=/(г), то для каждого частного случая м. б. выведены отдельные ф-лы.

Вводя второе допущение, что длина воспринимаемой волны значительно превосходит размеры 3. а. (Л»ж), заменяем синус его аргументом и получаем:

К S ²^Ψ¹ d^E₀^Sxdz =

τι 2jt;S

= Е₀ — cos φ.

Сравнивая полученный вывод с общеизвестным выражением Е_тах= E₀h_d_ (при приеме), получаем, что и при приеме, как и при излучении,

7 2nS "а.=—χ COS φ

для случая квази стационарного тока. При

*10

неквазистационарности, так же как и при излучении, имеем более сложные значения ft_d.j чем при квазистационарности.Так, для прямоугольника: h_d.=2h sin ^Лу. Беллини Р]

для 3. а., имеющей форму равнобедренного треугольника, дает выражение эдс при приеме любой длины волны, из которого легко вывести

^•=т[^г-ГТ2Т^тг.(8Р+24№*)Ч-Это выражение уже не симметрично относительно h к I; поэтому заостренный тр-к для приема выгоднее сплющенного. При больших λ сравнительно с I я h вторым членом в скобках можно свободно пренебречь, и

7 2 itS л получаем h_d=—, ф-лу, ранее выведенную для ква&истационарного тока.

Сравнение район и 3. а. Обе формы радиосетей являются замкнутыми; требуется определить пригодность их в том или в другом случае. Сточки зрения излу-ч е н и я характеризующим является параметр h_d_, связанный с излученной мощностью Р>,_зл.=Rua.iJl. соотношением

R_u„=m^^hf·

ггл 7 2 7lS

Так как h_d то несомненная выгод ность применения 3. а., обладающих большей сравнительно с рамками площадью, очевидна. Простой подсчет показывает, что реализация действующей высоты при заданной определенной длине провода I (что соответствует заданию собственной длины волны радиосети в определенном диапазоне) при помощи одновитковой 3. а. лучше сравнительно с рамкой, имеющей тот же общий периметр I и состоящей из п витков. Пусть и 3. а. и рамка—квадратной формы. Тогда сторона 3. а.=j-, ее площадь S=‘ ; для рамки из п витков сторона одного вит-^{кα= и} площадь я»=П · _г~=J-. Итак, действующая высота уменьшается пропорционально увеличению числа витков. На практике увеличение конечного эффекта (излучения и приема) для 3. а. получается еще большее, так как: 1) при той же длине провода полное сопротивление 3. а. примерно вдвое меньше, чем такое же сопротивление рамки (Баллантин [⁸]); 2) при той же длине провода волновой коэфф-т 3. а. почти вдвое меньше волнового коэфф-та для рамки (для последней λ=4,5-i-5,5 ί); поэтому имеется возможность при той же площади работать на волне меньшей длины, и,

следовательно, h_d_=²-j^S будет для 3. а. выгоднее еще и потому, что в этом случае м. б. выбран меньший знаменатель.

Параллельное включение нескольких витков ведет к дальнейшему повышению отдачи 3. а. При этом, чем больше брать параллельных контуров, тем короче волна вследствие взаимоиндукции между контурами и тем большую можно взять емкость: следовательно, тем большее количество энергии можно передать из генераторного контура, в 3. а. с целью повысить излучение послед ней. Одновременно уменьшается собственная волна 3. а.; по этой причине также повышается отдача 3. а. вследствие увеличения h_d. Опыт показывает, что п, где

1_п и 1_г—силы тока в 3. а. при п параллельно включенных и при 1 витке (п—число витков). Практика подтверждает большую целесообразность с точки зрения излучения применения 3. а. по сравнению с рамкой. Так, вращающийся радиомаяк (англ.), состоящий из 6 витков квадратной рамки со стороной 1,5 м, при рабочей λ=525 метров и при

2,5 kW на анодах ламп имеет момент тока в 7 метрампер, в то время как при 3. а. при 1,5 kW на анодах ламп, при двух параллельно включенных витках и площади пятиугольной антенны·^ 1 000 ж² получается момент тока ок. 70—80 метрампер.

С точки зрения приема 3. а. может быть сравниваема с рамками, включенными по той или другой схеме. Здесь, в противоположность применению антенн для излучения, когда всегда требуется настройка в резонанс излучающего контура с контуром, подводящим к нему энергию высокой частоты, м. б. две формы применения закрытого вида радиосетей: настроенные (3. а. и рамка) и апериодические; подробнее об этом см. Излучение и прием. К апериодич. схеме прибегают или для устройства многократного приема сигналов различной длины волны или при пеленгации для более устойчивой работы и устранения резких влияний—изменений в окружающей обстановке на точность пеленга (вследствие привносимой этими изменениями расстройки). При этом 3. а., обладающую большой h_d_, легко сделать апериодической без особого уменьшения ее воспринимающей способности; рамка, вследствие малости 1г_д_, не может пренебрегать выгодами работы при резонансе по сравнению с апериодической схемой. Поэтому многократный прием в последнее время всегда осуществляется при помощи апериодич. 3. а. или в схеме гониометра или контурами. Для пеленгации применимыми оказываются и резонансные схемы и апериодические; однако, 3. а. имеет перед рамкой то преимущество,что (в случае одного витка) она не имеет «бокового эффекта». Схемы включения 3. а. для пеленгации см. Гониометр и Пеленгаторы.

Сравнение 3. а. с открытой антенной. Понимая (смотрите выше) 3. а. как антитезу открытой антенны, можно высказать предположение, что 3. а. н для передачи является антенной будущего, точно так же как 3. а. почти вытеснила в последние 10 лет в области приема открытую антенну. Причиной предпочтения замкнутых форм антенны при приеме как профессиональном, так, часто, и любительском является большая свобода приема на эти формы радиосетей от атмосферных помех, помех других мешающих радиостанций и прочих источников, благодаря тому что 3. а. принимает направленно (теоретич. полярная диаграмма ее приема и излучения представляет собою две окружности, фигура 14); а в современной радиотехнике решающим фактором при установлении радиосвязи является не S, а отно-

Фигура 14.

шение ^S. ^{(сигнал)}. (смотрите Атмосферные помехи).

а (помеха;

Таким образом, при 3. а. выбором соответствующего положения ее в пространстве можно получить антенну с минимальной воспринимающей способностью с направлений помехи и хорошей — с направления корреспондента (фигура 14).

При излучении открытыми формами сетей имеет место круговое распределение мощности излучения (за редкими случаями направленных и притом сложных форм антенн). Поэтому сигналы, которые предназначены для определенного корреспондента, совершенно бесцельно излучаются и по всем другим азимутам, создавая не только излишнюю трату энергии, но и громадную помеху приему на близких к излучаемой волнах всем воспринимающим электрическую энергию устройствам в районе дальности действия (по кругу) данного передатчика. При передаче 3. а. направленность достигается наиболее простым и экономным способом: недостатки, указанные выше, почти полностью устраняются (в зависимости от той или иной остроты характеристики направленности). Сочетание эффектов (при приеме и при излучении) замкнутой и открытой форм антенн дает новые формы кривых направленности (смотрите Кардиоидные схемы).

Применение замкнутой антенны в области коротких и ультракоротких волн еще недостаточно определилось; пока известны лишь успешные схемы приема коротких воли на замкнутые формы антенн. Подробности о направленном действии различных форм 3. а. см. Пеленгаторы и Радиомаяки.

Лит.: ) Баженов В. И., Направляемый радиоприем, «Радиотехник», Н.-Новгород. 1919—21, 8—15; Сов. П. 353, 3251, 5261;^!) Б а ж e и о в В. И., Расчет замкнутых антенн, ч. 1, «ТиТбП», 1927, 43; ’) Б а ш е н о в В. I. и едов Н. А., Расчет замкнутых антенн, ч. 2, «Вестник теоретпч. и эксперимент. электротехники», М., 1929, т. 2, 3, стр. 90— 107;*) Mesny R., Usage des cadres et radiogonio-rnitrie, P., 1925; ^s) С л e п я н Л. Б., «ТиТбП», 1923, 22; ·) Dellinger J. И. and Pratt -Наг a de η, «Ргос. of the Inst, of Radio Eng.», New York, 1928, v. 16, 7; ⁷) Grover F. W. ibid., 1926, v. 14, 15, p. 733; *) Баженов В. И., Замкнутые антенны, «Радиолюбитель», Москва, 1926, 17—18. В. Баженов.