 > Техника, страница 47 > Затухание
> Техника, страница 47 > Затухание
Затухание
Затухание. 1) 3. в колебательном процессе — постепенное уменьшение амплитуды колебаний; получается при свободных колебаниях некоторой системы. Если эта система получила определенное количество энергии и тратит эту энергию во время колебаний, то имеют место затухающие свободные колебания. Примером таких колебаний могут служить колебания маятника. Потенциальная энергия, полученная маятником при отклонении его от точки равновесия, тратится во время колебания на преодоление сопротивления среды и на трение в точке подвеса, почему амплитуды колебания все время уменьшаются и колебания затухают.
Если сила F, действующая на материальную точку с массой т, пропорциональна расстоянию этой точки от нек-рого центра и направлена к центру, то отклонение х материальной точки из центра определяется дифференциальным ур-ием:
т Ш=F — — кх. (1)
Решение этого ур-ия дает незатухающее гармоническое колебание:
х=A sin (cui + ψ), (2)
где со=/I — угловая частота. Если зке помимо силы F на точку действует другая сила Flt пропорциональная скорости и про-тивополозкная ей по направлению, τ? 7 dx
I?1=_7cl dt ’
то ур-ие (1) превращается в ур-ие (3):
d*x
= — 7сж — 1ί
dx
Ч clt 1
(3)
к-рое имеет решение вида х= Ae~al sin (ωί + ψ), (4)
выражающее простейшее затухающее колебание, причем
k, ГкТ 7МГ “=2т> "=У т~ (,2т)
3. определяется членом e~at. Чем больше а, тем скорее затухают колебания. Величина а называется множителем 3. Амплитуды колебания убывают в геометрической прогрессии:
= Ае
αίι; гс2=Де_а(1,+ г); xs=Ae α(ί4
2Т)
и т. д., где Т--
- период колебания. От ношение двух следующих друг за другом через период амплитуд носит название декремента колебания и равняется
А=еаТ. (5)
Натуральный логарифм декремента колебания более удобен в обращении и поэтому чаще употребляется на практике. Он называется логарифмическим декрементом 3. (иногда—декрементом 3. или просто декрементом) и равен д= In Л=аТ. (6)
В электротехнике рассматривают собственные колебания контура, состоящего из емкости С, индуктивности L и сопротивления
R. Тогда свободные колебания силы тока г определятся из дифференциального ур-ия т ач Ь dt*
+ R
di 1 dt + С
г=О
(7)
интеграл которого г=Ie~at sin (cui -f φ), R
_ (8)
1=γ &Ικφ опреде ляются из начальных условий. Условием возникновения колебаний является
Ж 2/1·
Логарифмич. декремент 3. в разобранном случае, согласно ур-иям (6) и (1), равен
8=йТ· <»)
Применяя приближенную формулу Томсона для периода колебания
Т=-=2л: VLC,
получаем:
<5=nR y/ljr (9)
Иногда пользуются для вычислений ф-лой:
<5 =
150
КС
λ
(10)
полученной из (9), если выразить длину волны λ в м, сопротивление R в Ω, емкость С в см. Измерение логарифмич. декремента 3. производится при помощи специального прибора декреметра или путем снятия кривых резонанса (смотрите Измерения в радиотехнике).
Приведенные ф-лы для определения декремента 3. справедливы лишь для того случая, когда других потерь энергии, кроме потерь в сопротивлении R, нет. В контуре, однако, м. б. потери в диэлектрике конденсатора, на токи Фуко, на истечение, на излучение, а также потери в искровом промежутке (при наличии последнего).
Хотя декремент 3. относится лишь к затухающим колебаниям, он м. б. применен, однако, и в случае незатухающих колебаний, т. к. характеризует потери мощности. Действительно, энергия, находящаяся в колебательном контуре, W =, где Im—ам плитуда силы тока. Количество энергии, которое расходуется в течение одного полу-периода (то есть в течение одного колебания энергии, так как в течение одного периода мы получаем два максимума W), равно для незатухающих колебаний
Wr =
Отношение энергии, расходуемой в течение полупериода, к энергии, находящейся в контуре, равно логарифмическ. декременту 3.:
Wt>
<5=~· (Н)
В английской литературе часто берут от ношение энергии, расходуемой за период, к энергии, находящейся в контуре, вследствие чего в этом случае декремент получается в два раза большим:
<5=2<5=~ · Г.
Легко связать также декремент 3. с коэффициентом мощности cos φ. Действительно,
Λ _ rn πΚ
2 L шГ
T. о., если в контуре нет емкости, а есть лишь сопротивление и самоиндукция, то δ — π ctg φ.
Вывод ф-лы (11) для затухающих колебаний м. б. также применен, если принять во внимание, что для одного полупериода можно считать действующее значение силы тока
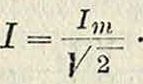
Для целого же ряда периодов действующее значение силы тока определяется из следующих соображений. Если число групп коле-
баний в секунду’ Ν, то, энергия N—, отданная в контур, расходуется в сопротивлении R, т. e. N=RP, или
<12)
Эта формула не вполне точна, но достаточна для практических расчетов.
Затухающие колебания получаются в контуре, содержащем искровой промежуток, который пробивается при определенном значении напряжения на конденсаторе. В радиотехнике имели применение сначала сильно-затухадлцие колебания с большим декрементом, затем—слабозатухающие. В настоящее время затухающие колебания применяются лишь на судовых радиостанциях (постепенно заменяющих затухающие колебания незатухающими от лампового генератора) и при измерениях. В последнем случае они возбуждаются в волномерах при помощи пищика (зуммера). О применении затухающих колебаний для связи см. Беспроволочная связь и Искровой передатчик.
Лит.: Петровский А. А., Научные основания беспроволочной телеграфии, 2 изд., ч. 1, СПБ, 1913; T homson W., «Pliilosoph. Magazine a. Journal of Science», L.—Edinburgh, 1853, ν. 5, ρ. 393; Feddersen λν., «Ann. d. Phys.», Lpz., 1861, В.113, ρ. 437, 1862, В. 116, p.132; Z e η n e c k J. u. R u k ο ρ H., Lehrbuch d„ drahtlosen Telegraphie, 5 Aufl., Stg., 1925; И о r t W., Technische Schwingungslclire, 2 Aufl., Berlin, 1922. И. Кпяцкин.
2) 3. электромагнитной волны вдоль линии наблюдается как уменьшение мощности волны от начала к концу линии. Если обозначить мощность в начале линии через Na, а мощность в конце линии через Ne, то затухание b линии определится в неперах (смотрите ниже):
b=In т ·
У Ne
Это выражение является общим и действительно для однородной и неоднородной пинии, в состав которой могут входить трансформаторы, усилители и т. д. Различают гл. обр. следующие затухания.
1. Относительное затухание, определяемое как разность затуханий двух систем
(две линии, два трансформатора и т. д.), из которых одна принята за эталон, то есть
b-bэт. (1)
Эта разность может быть положительной или отрицательной.
2. Собственное затухание, определяемое как затухание системы (линия, трансформатор и т. д.), замкнутой на конце сопротивлением, равным волновому сопротивлению ,т.е.
= 1п
|Уа/а| · COS
I VeIei cos
*=ΐητΛ]^μ
ψ V Tel
= In
Ύ Ie “*P Neгде Va, I и, Ve и Ie—напряжение и сила тока в начале и конце линии.
3. Эффективное затухание, определяемое как натуральный логарифм корня квадратного из отношения
I УеП I
IУ eh I ’
где I VeIe — число вольтампер в цепи приемника, когда генератор работает непосредственно на приемник и внутреннее сопротивление генератора равно сопротивлению приемника, a |ГД<,|—число вольтампер в цепи приемника, когда между генератором и приемником включена линия, то есть
(2)
Ьэфф- lnJ vje (3)
Весьма употребительно также выражение для затухания по току и по напряжению, представляющее собой натуральный логарифм отношения амплитуд" токов или напряжений в начале и в конце линии:
>=In
Ι-ΓαΙ.
Ь=In
iva|
h ’ " lVe (4)
Величина b называется коэффициентом затухания линии, имеющей длину I км. Разделив 6 на ί, получим β—кило-метрич. затухание линии. Делогарифмируя ур-ия (1), (2), (3) и (4) получим выражения еь=е1*1 и, при 1=1, еь= е^> которые называются множителями затухания.
Лит.: Юрьев М. Ю., Теория телефонных цепей, М., 1925; Круг К. А., Основы электротехники, М., 1926; К о в а л е н к о в В. И., Телефонирование на большое расстояние, ч. 1 (на правах рукописи), Л., 1925; Wagner К. W., Elektromagnctische Aus-gleichsvorgange In Freileitungen u. Kabeln, Lpz.—B., 1908; BrcisigF, Theoretische Telegraphic, 2 Aufl., Brschw., 1924; Ollendorff F., Die Grundlagen d. Hochfrequenztechnik, B., 1926; Hill J. &., Telephonic Transmission, L., 1920; F e i g e A., Allge-meine Vierpoltheorie, «Telegraphen- und Fernsprecher-Technik», B., 1927, 3, 9, 12] Strecker K., I-Iilfs-buch f. die Elektrotechnik, B. 2, 11 Aufl., B., 1928; Comite consultatif international des communications tdieph. и grande distance, P., 1926. Ю. Ридель.
3) Единицы передачи. По постановлению Мезкдународного консультативного комитета по телефонированию на далекие расстояния в настоящее время приняты две единицы 3. (единицы передачи): единица, выраженная как натуральный логарифм квадратного корня из отношения мощностей в начале Na и в конце Ne четырехполюсно го контура, b
= In ΐ N",
V Ne’
так называемый непер, и единица, выраженная как десятичный логарифм той зке величины Ь=
=lg -i, так называется бель. На практике
У
пользуются Vio 9т°й единицы—децибелем, совпадающим с ранее принятой в Америке единицей T.U. (Transmission Unit). До последнего времени существовала еще одна единица передачи—миля стандартного кабеля (м. с. к.). Для перевода одних единиц в другие можно пользоваться следующей таблицей:
1 непер=8,7 децибеля (8,7 Т.и.)=9,18 метров с. к.
1 децибель (1 Т.и.)=0,115 непера=1,055 метров с. к.
1 метров с. к.=0,109 непера=0,95 децибеля (0,96 T.U.)
В СССР, Германии и Швеции пользуются единицей непер; в Англии и С. III. А”.—децибель. Самое определение непера и беля показывает, что эти числа не имеют постоянного значения и зависят от 3. передаваемого колебания. Выбор этих определений обусловлен удобством применения непера и беля для вычислений. н. Баев.