 > Техника, страница 48 > Змей воздушный
> Техника, страница 48 > Змей воздушный
Змей воздушный
Змей воздушный, привязной летательный аппарат, поддерживаемый в воздухе давлением ветра на его поверхность, поставленную под некоторым углом к направлению движения ветра. Теория воздушного змея впервые была предложена Т. Буа (Th. Bois), "разработавшим ее на основе формулы сопротивления воздуха, данной Ланглеем (Langley).
Равновесие воздушного змея обусловлено действием трех сил: силы тяжести змея—Р, силы давления ветра на поверхность воздушного змея — R и силы натяжения нити Т, привязанной к змей в некоторой его точке. Для равновесия змея необходимо, чтобы геометрическая сумма всех действующих сил равнялась нулю:
Р + Д + Р-0. (1)
Геометрия. сумма двух первых сил дает силу тяги змея Τ, которая в положении равновесия уравновешивается натяжением нити Т.
Уравнение (2) определяет абсолютную величину тяги воздушного змея, а также силы натяжения нити:
T=P + R. (2)
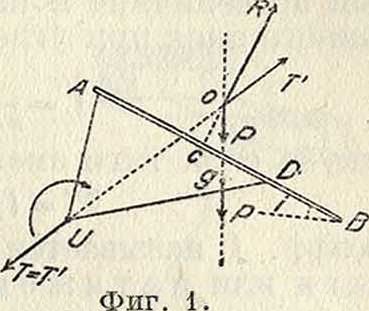
Общая схема расположения сил представлена на фигуре 1, где АВ—поддерживающая поверхность змея и г—угол атаки, образованный поверхностью с направлениемветра.
Сила тяжести Р и сила давления ветра R, приложенная в центре парусности с дают равнодействующую Т с направлением ОТ. Для равновесия 3. в необходимо, чтобы равнодействующая Т уравновешивалась натяжением нити Т. Отсюда следует, что точка привязи нити должна находиться где-нибудь на направлении ОТ, наир, в точке U. Точка привязи нити к змей называется узлом. На практике за узел U обычно принимают точку, лежащую за пределами конструктивных частей змея. В последнем случае прибегают к устройству т. н. у з д е ч к и. В двух или нескольких точках змея прикрепляют отдельные нити UA, UD,., называемые путами; другие концы собраны в точке ύ в общий узел, к к-рому прикрепляется основная змейковая нить. Змей, привязанный в узле U, может вращаться около него, изменяя угол атаки г. Так как сила натяжения нити Т проходит всегда через узел U, то вращение змея обусловливается только влиянием моментов сил Р и R. Приравнивая сумму моментов этих сил относительно узла нулю, мы получим второе основное ур-ие равновесия, определяющее угол атаки змея:
Ми(Р) + Ми (Д)=0. (3)
Так как сила Р постоянна по величине и направлению, а сила R по направлению зависит от угла атаки змея i, а по величине—от площади поддерживающей поверхности S и от скорости ветра г> и, кроме того, от ,« (коэфф., равный отношению плотностей воздуха вверху и у поверхности земли, μ =.
то величина силы тяги T змея определится уравнением:
Τ=Р + S>Si?2, (4)
где S—площадь в м2, υ—скорость ветра в м/ск, a Kt—коэфф. полной силы, или
μβν·
T=4 + к,
μν2 · 9
(5)
где <5=g ; это отношение (вес, приходящийся на единицу поверхности змея) принято называть плотностью змея.
Приняв
f
μ Sv2
получим :
Складываем векторы ур-ия геометрически, по методу замкнутого тр-ка, пользуясь для вектора К,- кривой Лилиенталя L данного
| <5
,=« и -~=р, |
(6) |
| t=p + Kt. | (7) |
змея (фигура 2). Предполагая направление ветра горизонтальным, вектор силы тяжести
00=р =~^з будем откладывать вверх по вертикали Оу от полюса О. Проведя из полюса О произвольный вектор Кь получим равнодействующий вектор I, пропорциональный по величине и направлению силе тяги данного змея при угле атаки гп. Этот вектор
t=.·£ · (8)
μδν*
откуда сила тяги змея
Т=t /mSv2
(9)
Коэфф. t называется коэффициентом т я г и или натяжения. Угол β этой тяги
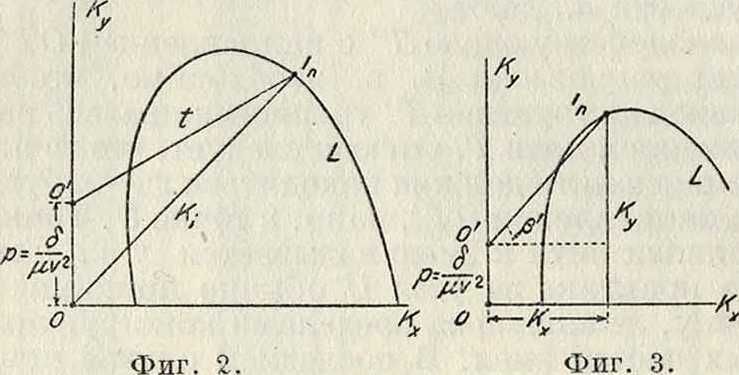
с горизонтом (фигура 3) определяется или непосредственным измерением по чертежу или, более точно, по ф-ле:
й
tg0=-
= Ку ___
(10)
Κχ К х Κχμν>
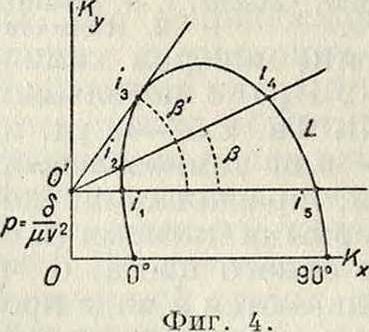
где Ку и Кх—коэфф-ты подъемной силы и лобового сопротивления (смотрите Аэродинамика). Касательная, проведен, из полюса О к кривой L, дает наибольший угол β, возможный при данном значении р=;, причем в точ ке касания получим соответствующее этому случаю значение г3 (фигура 4) угла атаки змея. Проводя из полюса О секущие, находим, что каждому направлению β силы тяги соответствуют два различных угла атаки змея, причем большему углу атаки соответствует и больший коэфф. тяги и, следовательно, большее натяжение; углы атаки, меньшие значения г3, называются углами м а-л ы х натяжений. Из рассмотрения фигура 4 видно, что на угол тяги β, npHt=Const,
влияет величина р=~. Чем этот вектор меньше, тем угол β тяги получается больше. Отсюда следует, что при i=Const угол тяги тем больше, чем меньше плотность δ змея, чем больше скорость ветра и чем больше величина μ, то есть чем ниже летает змей. Проведя из полюса О горизонтальную секущую, найдем в точках пересечения этой секущей с кривой L углы атаки и гь, соответствующие β=0. Если мы имеем дело с нек-рым определенным змеем у поверхности земли, то имеем <5=Const и μ= 1=Const, и значение вектора р, таким образом, будет зависеть только от скорости ветра v. Следовательно, если змей привязан, то при данной скорости ветра и углах атаки гх и г5 змей не может подняться выше лебедки.
Предельный ветер. Исследуя
<5
влияние величины вектора р=—г на значения предельных углов горизонтального натяжения, можно заметить, что при уменьшении скорости ветра v значения предель-ных углов сближаются между собою. Может случиться, что при нек-ром значении скорости ветра вектор р будет равен наибольшей ординате Y=Ky кривой L. В таком случае ни один вектор, проведенный из полюса 0 к кривой L, не даст в этом случае для угла натяжения β значения, большего 0° (фигура 5). Это показывает, что для каждой
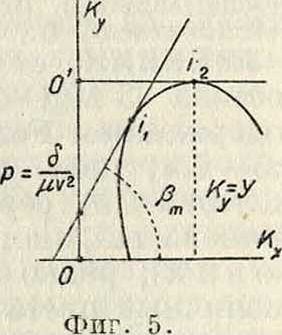
данной конструкции 3. в и данного значения δ (при μ=1) существует такая определенная минимальная скорость ветра vminтак называемым предельный ветер, при котором ни при каком угле атаки змей не может подняться от земли. Для возможности его взлета (при μ=1) должен быть удовлетворено а условие: < У; отсюда для скорости ветра получим условие:
v > ]/~у · (И)
Таким образом, предельный ветер
V,nin=/у И <5=YVmin (12)
Отсюда видно, что змеи различных конструкций, но одинаковой плотности могут иметь одно и то же значение для предельного ветра, если наибольшие ординаты кривых L будут одинаковы. Для большинства 3. в плотность δ колеблется между 0,5 и 1,5, а Г=0,05-1-0,08.
Конструкция 3. в Каждый 3. в состоит из поддерживающей поверхности, привязного каната (или нити), уздечки, служащей для прикрепления каната к змею, и органов устойчивости. Привязным канатом, наматываемым на катушку или особую лебедку, могут служить обыкновенная вая веревка (для небольших змеев), стальная проволока или стальной трос. В приведенной ниже таблице указаны вес и прочность на разрыв вых веревок и стальных тросов различного диаметра, применяемых для привязывания 3. в.
Вес и прочность на разрыв вых веревок и стальных тросов.
| вая веревка | Стальной | трос | |||
| диам. в миллиметров | вес 1 метров веревки в г | разрывн. усилие в килограммах | диам. в миллиметров | вес 1 метров троса в г | разрывн. усилие в килограммах. |
| 4 | 13 | 200 | 2 | 1S | 270 |
| 6 | 32 | 450 | 3 | 38 | 550 |
| 9 | 70 | 950 | 4 | 70 | 980 |
| 12 | 125 | 1 500 | 5 | 107 | 1 600 |
| 15 | 200 | 2 400 | 6 | 145 | 2 300 |
| 20 | 320 | 3 600 | 7 | 200 | 3 200 |
Уздечка состоит из двух или более тонких канатов, на которые разветвляется конец главного каната (леер), что способствует сохранению устойчивости, т. к. точка пересечения продолжения каната с плоскостью змея (т. н. теоретич. точка укрепления змея) получает в этом случае возможность перемещаться при различных наклонах плоскости.
По устройству поддерживающей поверхности 3. в могут быть подразделены на одноплоскостные, много плоскостные и составные. Простейшим видом одноплоскостных 3. в являются распространенные в СССР змеи, состоящие из материи или бумаги, в ви- де прямоугольной плоскости, натянутой на кресто-
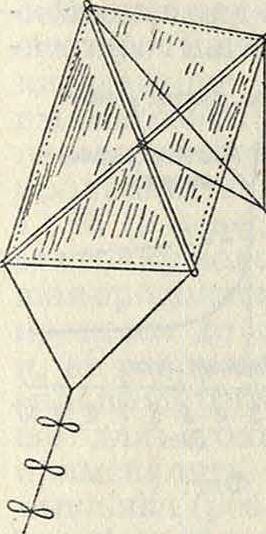
Фигура 6.
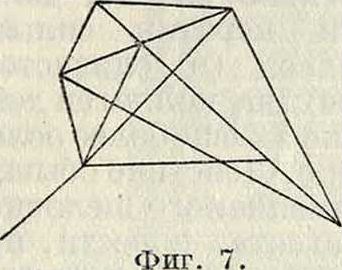
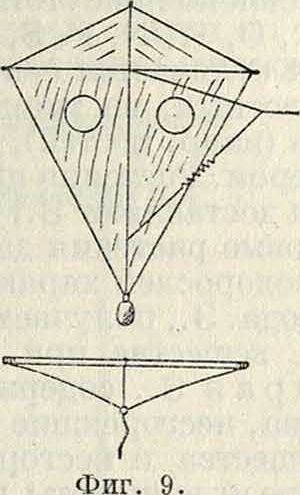
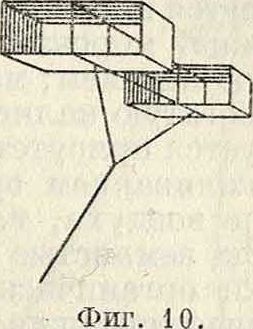
образный каркас; к двум углам нижнего края для сохранения продольной устойчивости прикреплен хвост (фигура 6). Французский змей (фигура 7) имеет грушевидную или ромбич. форму. Для увеличения поперечной устойчивости на 3. в устанавливают килевые плоскости, параллельные плоскости леера, а несущую поверхность делают выпуклой или в виде широко раскрытого двугранного угла; такие змеи известны под названием «малайских змеев» (фигура 8). Кроме этих мер, для увеличения устойчивости З.в., в плоскости змея устраивают иногда окна (отверстия) для уменьшения в нужных частях напора ветра (фигура 9—3. в системы Ольховского). Для той же цели в некоторых случаях устраивают эластичную уздечку путем включения в нижнюю ветвь ее резинового кольца. Много плоскостные 3. в.—этажерочные, коробчатые и ячеечные. Примером эта-жерочного типа может служить змей Лекорню, состоящий из ряда плоскостей, расположенных одна над другой и соединенных между собой боковыми вертикальными плоскостями. Большое распространение в СССР и за границей имеет коробчатый змей Гарграва (фигура 10). Он состоит из двух отдельных коробок без дна, находящихся на общем бруске и расположенных на нек-ром расстоянии одна от другой. Благодаря хорошей устойчивости коробчатый змей весьма часто применяется при метеорологических и аэрологических измерениях. Ячейковый змей представляет собой плоскости, разбитые на отдельные элементы, благодаря чему подъемная сила увеличивается не за счет увеличения размеров несущей поверхности, а за счет увеличения числа ячеек. Из таких змеев известна конструкция Лекорню и Грахама Белля. Змей Грахама Белля состоит из отдельных элементов, имего-
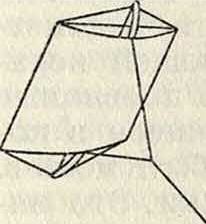
Фигура 8.
щих вид тетраэдра. Четыре таких элемента, соединенных по углам, образуют более сложный тетраэдр, к-рый в свою очередь может служить элементом для составления еще большего тетраэдра, (фигура 11).
Составны е, или групповые, 3. в представляют собой группу змеев, соединенных между собой в одну гибкую систему.
Применение 3. в Кроме” спорта, 3. в применяются: на метеорологич. станциях для исследования высоких слоев атмосферы (до 7 000 и даже 10 000 м) при помощи поднятых на змеях самозаписывающих приборов; для производства фотографических съемок местности, для сигнализации, для установки антенны беспроволочной связи и, наконец, для совершения подъемов с целью наблюдения. В последнем случае в змеях устраивают органы управления для изменения угла наклона поддерживающих
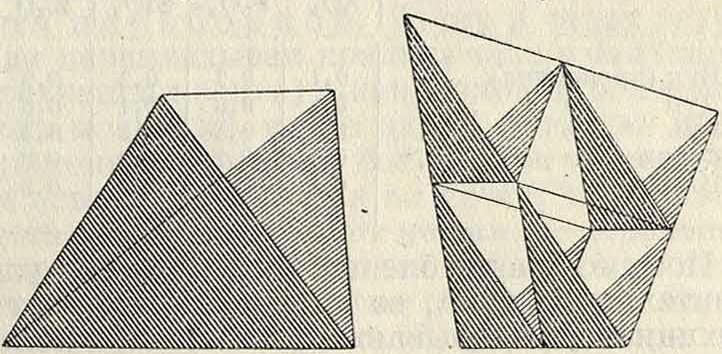
Фигура н. поверхностей, чем достигается изменение высоты подъема. Таким органом служит вспомогательный леер, прикрепляемый к нижнему краю поддерягивающей поверхности. Обычно для подъемов с целью наблюдения пользуются групповым 3. в.
Лит.: Грибоедов С., Устройство змеев, теория и их применение к исследованию высоких слоев атмосферы, сборник «Воздухоплавание и исследование атмосферы», под рсд. Поморцева, СПБ, 1897, вып. 2; Б е р т и п е, Теория воздушного змея, «Инж журнал», СПБ, 1892, 1; Ольховский В., Современные воздушные змеи, «Воздухоплаватель», СПБ, 1912, 2, 4, в; Яркове к и и В. И., Летательные аппараты. СПБ, 1913; Соколов П., Теоретич. основы змейковых подъемов, «Труды Аэростатного отдела Летучей лаборатории», М., 1918, сборп. 1; е г о ж е, Графич. метод решения задачи о наибольшей высоте воздушного змея, там же; Кованько А., Воздушные змеи, «Циклист», СПБ, 1899, 42; Корреи W., Bericht ilbcr d. Erforschung d. ireien Atmosphare mit Hilfe v. Draclien, «Aus d. Archiv d. Deutschen Seewarte». Hamburg, 1901, Jg. 24; Wegener K., Die Teclmik d. Drachenaufsteige, «Ergebnisse d. Arbei-ten d. Kgl. Preuss. aeronautischen Observatoriums bei Lindenberg», Brschw., 1905, В. 1; Lecornu .T., Les ccrfs-yolants, 2 Cd., P., 1910; В о is Til., I.es cerfs-volants et leur application, «Revue du G6nie», Paris, 1905, aotit; Saeonney, Cerfs-volants mili-taires, «Revue du G6nie militaire», P., 1909; Fuji-w a r a S., About Kites and Kite-Strings, «Journal of the Meteorological Society of Japan», Tokyo, 1910, 29-til Year, 9. А. Знамгнсний.