> Техника, страница 48 > Зубчатые колеса

Зубчатые колеса

Зубчатые колеса служат для передачи работы и вращения от одного вала к другому с заданным отношением угловых скоростей. Колесо, получающее вращение извне, называется ведущим; второе колесо, получающее вращение от первого,—ведомым. Если угловая скорость ведущего колеса есть ω_χ, а ведомого ω₂, то -=к называется передаточным числом. Постоянное отношение —=к

(О 2

осуществляется круглыми колесами,

а именно: при параллельных осях вращения—ц илиндрическими, при пересекающихся осях—к о н и ч е с к и м и и при перекрещивающихся осях—гиперболо-идальными и винтовыми 3. к. и червячной передачей. Переменное к осуществляется некруглыми колесами (эллиптическими, овальными и тому подобное.), которые применяются обычно только при параллельных осях. Круглые 3. к. находят преимущественное применение. Из них чаще всего встречаются цилиндрические колеса.

I. Цилиндрические колеса.

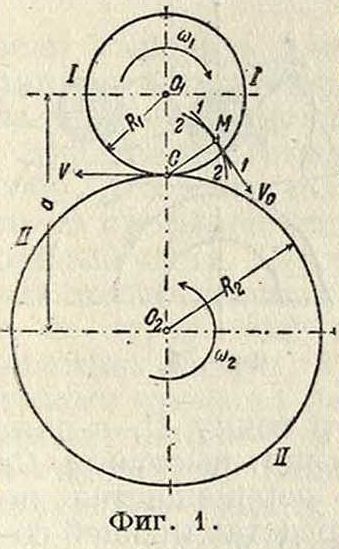
1. Теория зацепления. Относительное движение двух систем, вращающихся около параллельных неподвижных осей спостоянным отношением угловых скоростей=1с, есть движение плоское, определяющееся вполне центроидами в виде двух окружностей, которые перекатываются одна по другой без скольжения. Точка С касания окружностей —· мгновенный центр вращения в относительном движении систем—имеет одну и ту же скорость v в обеих системах: v=(o_rR_l=<a₂R_i(фигура 1). При заданном расстоянии а между центрами 0₁и О₂, положение точки С определяется от-

ношением:=—=к, то есть

Ri ω₂

точка С, называемая полюсом передачи, делит расстояние между центрами на отрезки, обратно пропорциональные угловым скоростям. Окружности I-Ι и ΙΙ-ΙΙ имеют важное значение в теории зубчатых колес и называются делительными, или начальными, а соответствующие им цилиндры—начальными цилиндрами. Начальные цилиндры снабжаются зубцами, при помощи которых и происходит передача работы и движения. Зубцам дают обычно симметричную форму, очерчивая их с боков одинаковыми профилями (фигура 2). Часть

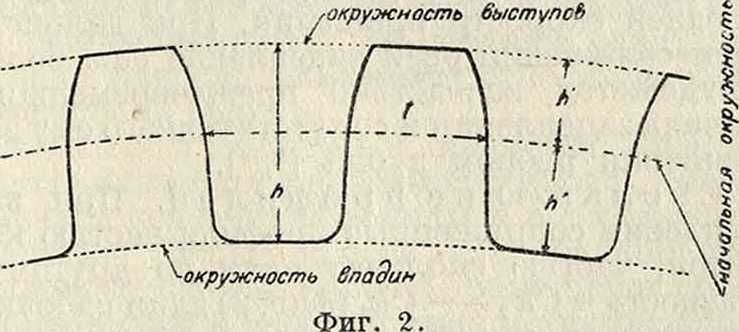
зубца,расположенная над начальной окружностью, называется головкой, под начальной окружностью—н о ж к о й.

Расстояние между двумя смежными соответственными профилями, измеряемое по начальной окружности, называется шагом зацепления и обозначается через i. Если число зубцов на колесе есть z и радиус начальной окружности 11, то ‘ZnR=zt, откуда /с=Для определения раз-

меров колеса удобнее, однако, пользовать ся величиной модуля зацепления, т= _я, а не шага t; тогда расстояние между осями α= - - ---. Выражается то всегда в мм. Основные размеры колеса и зубцов, а также инструментов для нарезания зубцов выражают через то. Высота головки зубца

(фигура 2) h=m; высота ножки h"=^η т==1,167 то, до 1,2 то; полная высота зубца h=‘zl т=2,167 то, до 2,2 тонны Толщина точно

О

изготовленного зхбца, считая по начальной окружности, равна *=; для грубо из готовленных 3. к. толщина зубца равна 0,48 ί, а ширина впадины—0,52 t.

В Америке вместо модуля пользуются обратной величиной, к-рую называют диаметральным шагом (diametral pitch); в русской практике величину эту обычно называют английским словом «п и т ч». Обозначая его через р, имеем: р=~, где R выражается в дюймах (между тир существует следующая простая зависимость: т-р== 25,4). В целях ограничения необходимого для нарезания зубцов количества инструментов почти во всех странах установлены нормальные ряды значений для т. Проектом, разработанным для СССР, намечен следующ. ряд, близко совпадающий с принятым в Германии по норме DIN 780: от 0,3 до 1 миллиметров- через 0,1 миллиметров; от 1 до 4 миллиметров—через 0,25 миллиметров; от 4 до 7 миллиметров—через 0,5; от 7 до 16 миллиметров—через 1; от 16 до 30 миллиметров—через 2; от 30 до 45 миллиметров— через 3 миллиметров; дальше—через 5 миллиметров. В С. III. А. и Англии принят следующий ряд значений р: от 1 до 3 через ¹/₄, далее—З¹/., 4, 5, 6, 7, 8, 9, 10, 12, 14, 16, 18 и 20.

Общие законы зацепления. Профили, работающие друг с другом, называются сопряженными. В соответствии с основным требованием-£- =/с, которому должны удовлетворять сопряженные профили, устанавливаются те геометрич. условия, которые определяют их очертание. Если профили 1-1 и 2-2 находятся в соприкосновении в некоторой точке М (фигура 1), то относительная скорость v₀ в точке касания должен быть направлена по общей касательной к профилям, в противном случае профили или разойдутся или врежутся один в другой, что недопустимо. Т. к. точка С является мгновенным центром в относительном движении профилей, то СМ будет нормалью. Т. о., профили должен быть выбраны так, чтобы общая нормаль к ним в точке касания проходила через полюс передачи. Задавая один из профилей произвольно, можно на основании приведенной теоремы построить другой—сопряженный. Общий метод такого построения был указан Рело. В действительности для профилей зубцов применяют только два рода кривых: i) циклические кривые и 2) эвольвенту круга—как наиболее простые из сопряженных кривых по способу их образования и по геометр ич. свойствам.

Ц и к ли ческое зацепление (фиг-3). При качении производящей окружности 1-1 по начальн. 11-11 точка С первой опишет на плоскости 11-11 эпициклоиду (эпитрохоиду)

Се₂; та же точка С вычертит гипоциклоиду (гипотрохоиду) Сд_х на плоскости 1-1, если окружность 1-1 будет катиться по 1-1. Аналогичным образом точка С производящей окружности 2-2 вычертит: 1) эпициклоиду Се₁ на плоскости I-Ι и 2) гипоциклоиду Сд₂на плоскости 11-11.

Представим себе профиль Се₁ в новом положении C₁e,. Он пересекает производящую окружность 2-2 в точке а. Очевидно — Сс_г= =-Са. Соответствующее положение профиля Сд₂определится условием:--(7с₂=~ Сс_1у значит, — Сс₂=~ Са, то есть оба профиля касаются в точке а и прямая аС—их общая нормаль. При зацеплении профилей перед линией центров гипоциклоида Сд_г ножки будет работать с эпициклоидой Се₂ головки, и точка касания профилей опишет дугу производящей окружности 1-1. За линией центров эпици-

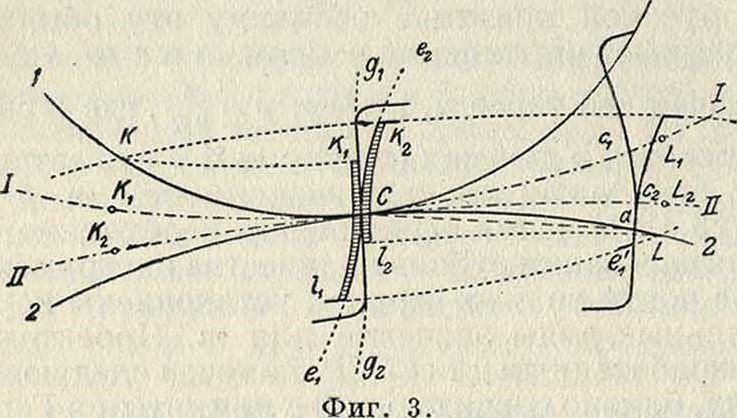
клоида Се_у будет работать с гипоциклоидой Сд₂, и точка касания пойдет по окружности 2-2. Дуги производящих окружностей представляют собою геометрич. место точек касания сопряженных профилей в неподвижной плоскости, к-рое носит название линии зацепления. Линия зацепления дает исчерпывающую характеристику профилей и их взаимной работы. Чем проще вид линии зацепления, тем проще соответствующие ей профили как по закону образования, так и по геометрич. свойствам, и наоборот.Начало зацепления профилей определяется точкой К пересечения линии зацепления с окружностью выступов ведомого колеса 11-11, а конец—точкой L пересечения линии зацепления с окружностью выступов ведущего колеса 1-1. Сумма длин дуг ^KC+^CL дает длину е линии зацепления. Снося точку К дугой радиуса О_гК на профиль Сапожки колеса 1-1, получим точку к_1у которая находилась в зацеплении с вершиной /с₂ ведомого профиля в точке К аналогичным образом получаем точку 1₂ на профиле ножки Сд₂, работающей с вершиной 1_г ведущего зубца в точке L. Отмеченные на фигуре 3 двойными линиями участки k_xCl ₁ и fc₂Ci₂—рабочие участки профилей. Часть профиля ножки, лежащая между окружностью впадин и точкой к_г (соответственно i₂), никогда в зацеплении не участвует и м. б. очерчена совершенно произвольно, с одним лишь условием—чтобы путь, описываемый вершиной сопряженного зубца, не врезался в тело ножки. В соответствии с этим следует построить удлиненную эпициклоиду, описываемую вершиной сопряженного зубца, и принять ее за профиль неработающей части ножки; построение удлиненной эпициклои ды м. б. выполнено приближенно [¹⁴]. Часто очертание ножки переходит закруглением с радиусом равным 0,1 t в окружность впадин.

Для вычерчивания профилей наносят на начальной и производящей окружностях ряд равных небольших делений, начиная от точки С. Из каждого деления начальной окружности, как из центра, радиусом, равным расстоянию точки С до соответствующего деления производящей окружности, описывают ряд дуг; огибающая всех этих дуг дает эпициклоиду при качении производящей окружности снаружи начальной окружности и гипоциклоиду—внутри ее. На зубчатой рейке получаются циклоиды над и под начальной прямой. При черчении в большом масштабе пользуются для спрямления дуг одним из правил Ранкина. Радиусам ρ производящих окружностей дается обычно значение: ρ=(0,35-ρθ,4) й. Увеличению ρ препятствует ослабление зубца у основания. При ρ, равном 0,5 й, ножка получает прямо лшт. очертание по ра -диусам начальной окружности. При дальнейшем увеличении ρ ножка еще фигура 4.

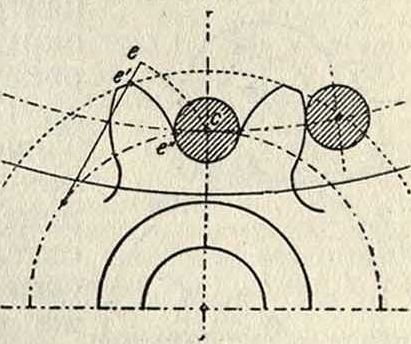
более суживается и при ρ=и обращается в точку С, к-рая, при зацеплении с эпициклич. выступом Се сопряженного профиля, перемещается по начальной окружности, представляющей собою линию зацепления (фигура 4).

Взяв вместо точки равноотстоящую кривую—круг и вместо эпициклоиды Се равноотстоящую ее", получим цевочное зацепление. Одним из частных случаев цевочного зацепления является передача Гриссона (смотрите Гриссоиа передача).

3. к. с циклическими профилями весьма чувствительны к неточностям установки. Наир., при увеличении расстояния между осями на 1 миллиметров, при т= 10 миллиметров и радиусах производящих окружностей ρ_χ=ρ₂=у--,

получаются колебания скорости в 4% от средней скорости вращения. При дальнейшем сближении осей зацепление еще более ухудшается вследствие преждевременного начала зацепления и сопутствующего ему зацепления ребром зубца [V⁴].

Скольжение профилей. При зацеплении сопряженные профили частью катятся, частью скользят один по другому. Разность — Ск₂ — — Ск_г (фигура 3) длин рабочих участков профилей дает абсолютную величину скольжения профилей при работе их перед линией центров, а ~ ΟΙχ— ~ С1₂—соответственно, за линией центров. Точка касания проходит по сопряженным профилям разные пути за один и тот же промежуток времени. Если взять сопряженные профили в произвольный момент зацепления, то за время dt по ведущему профилю будет пройден путь dl_lt а по ведомому—cU₂. Разность ctt₂ — cUx даст абсолютное скольжение по ведущему профилю, а <Μχ — άλ₂—по ведомому. В основу оценки скольжения кладется относитель-

ное, или удельное, скольжение д, величина которого определяется для первого профиля отношением

άλ₂ - <2Л,

У¹ ~ ~~Ш1 ’

а для второго

άλ, — άλ₂

~йГ

Относительное скольжение—величина переменная, зависящая от формы профиля. Величину его можно определить аналитически,

если выразить длину λ дуги профиля в полярных координатах с началом в центре начальной окружности.

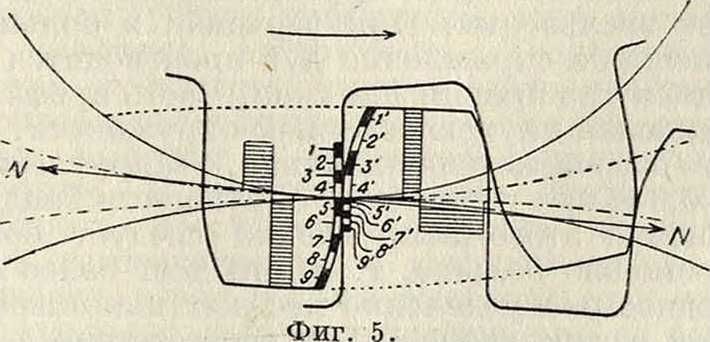
Обычно прибегают к приближенному способу. Для этого делят рабочие участки одного из профилей (например ведущего) на малые равные части. Через линию зацепления сносят точки деления на ведомый профиль и т. о. определяют на нем соответствующие участки. На фигуре 5 рабочая часть ножки ведущего профиля разделена на 4 равные части, а головки—на 5 частей; деления ножки и головки не равны между собой. Соответствующие участки профилей обозначены на фигуре 5 одинаковыми цифрами. Длины участков ведущего профиля обозначаем через К, К, К,-, а ведомого, соответственно, через λ/, λ₂, λ£,. Приближенное значение относительного скольжения на первом участке ведущего профиля л=^λϊ ~

Ух д »

а ведомого

0Г-

Для второго участка: K’ - я.

^И 02=

К “ ^У2 " K и т. д. Вычислив величины относительных скольжений для всех участков и отложив их на перпендикулярах от средних радиусов зубцов, наносят диаграммы относительного скольжения (фигура 5).

Износ профилей является следствием скольжения и качения профилей, находящихся под действием силы N нормального давления. Степень износа, то есть толщину отделяемого слоя материала, принимают пропорциональною работе трения и обратно пропорциональною величине подверженной изнашиванию поверхности. Работа трения равняется fN(dX₂— dAj); величина изнашиваемой поверхности, при ширине обода равной 1, будет di. Тогда степень износа ведущего профиля

Уг=fci · fN ^dh ~ ^dK

а ведомого

άλ_χ

У i=&ι · fN —²

Коэфф. k_u зависящий от материала зубцов и их формы, принимают для простоты по стоянным. Т. о., степень износа оказывается пропорциональной удельному скольжению. За неопределенностью коэфф-та /с_х невозможно определить абсолютное значение степени износа; можно лишь указать его характер, что само по себе дает достаточно ясные указания для целесообразного проектирования профилей.

Дугой зацепления называется дуга начальной окружности, на к-рую повернется колесо за время зацепления одной пары профилей. Сута~ К_гС + ~CL₁=~KC + + -CL=^K_vL₁ или ^K₂C+^CL₂=-KC + + CL=— K₂L₂ (фигура 3) дает длину S дуги зацепления. Для циклич. профилей S=e. Отношение длины S дуги зацепления к шагу f называется пр одолжительностью, или плавностью,зацеп лени я, σ=® ;

а определяет в среднем число пар зубцов, находящихся одновременно в зацеплении; для непрерывной работы необходимо, чтобы продолжительность зацепления в была <С 1. Величина σ является весьма важной характеристикой работы пары 3. к., так как позволяет судить о распределении передаваемого усилия между зубцами.

Из рассмотрения фигура 3 ясно, что для циклич. зубцов S и а зависят от: 1) радиусов

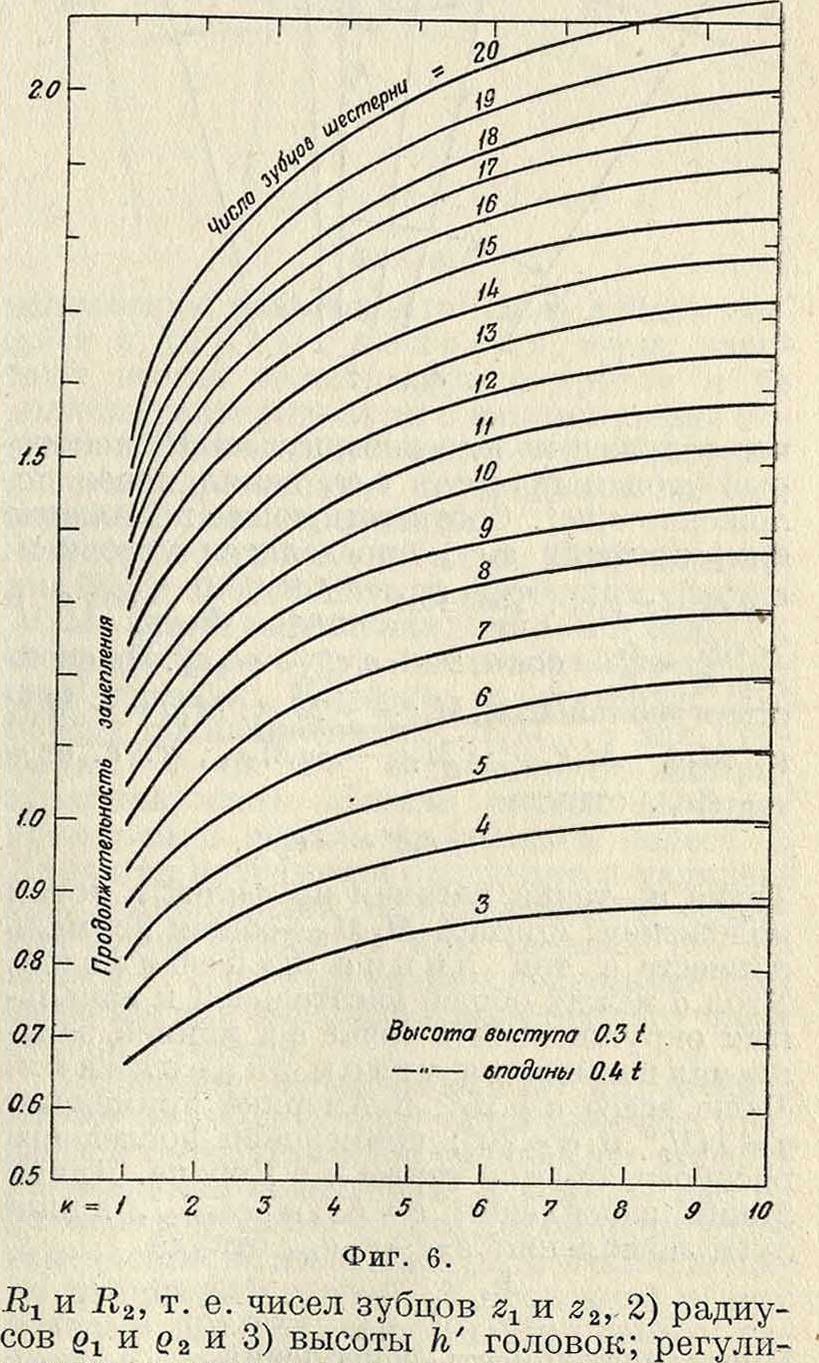
руется значение а надлежащим изменением числа зубцов. Диаграмма, изображенная на фигура 6, дает зависимость σοτ z₁ и fc=— -

Эвольвентное зацепление (фигура 7). Точка о производящей прямой М_ХМ₂опишет: 1) на плоскости колеса, 1-1 эвольвенту βχΟβχ—при качении прямой по основной окружности 1-1 и 2) на плоскости 11-11 эвольвенту е₂се₂—при качении прямой по основной окружности 2-2. Допустим,

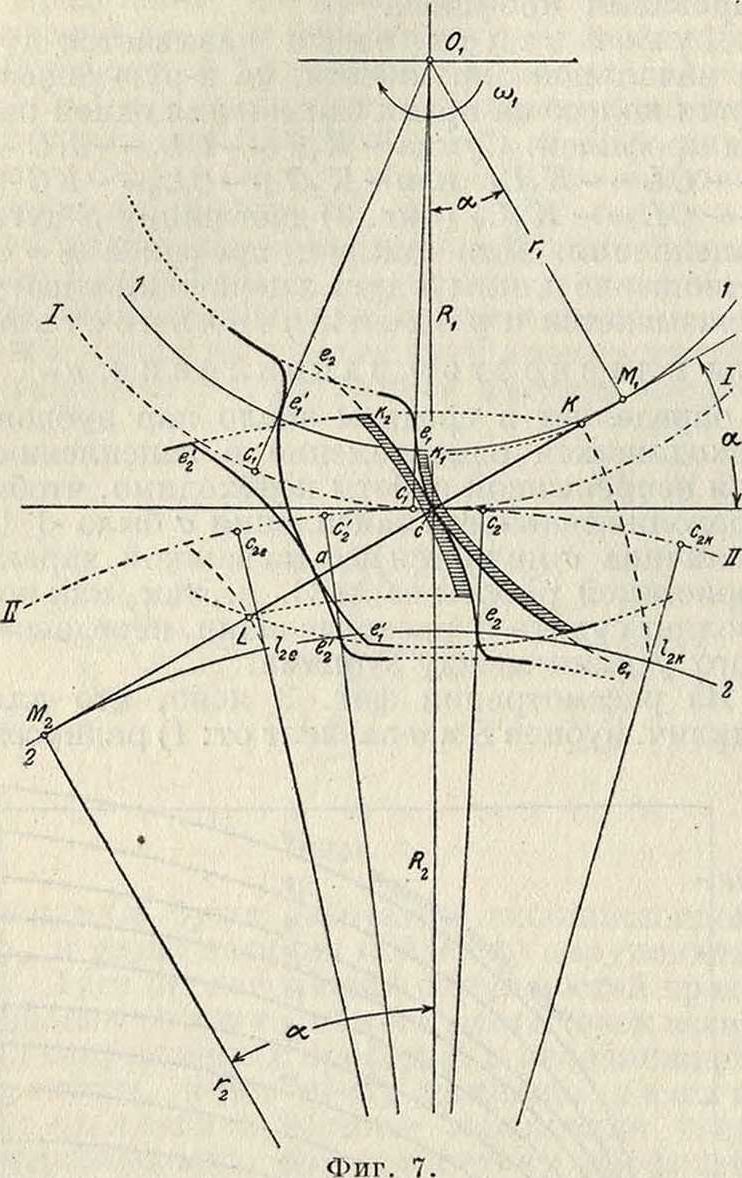
что ведущее колесо повернулось на некоторый угол и профиль е₁се₁ занял новое положение е[ае{. Соответствующее положение «₂ае₂ профиля е₂се₂ определится условием:

— с₂с₂=— с,с[. Так как=£’=cos а и

= cos ^α> то “ «i e;=— е,в₂. По свойствам эвольвенты,М]С=— М^, М_лα= — Μ·β[ и M^a — M-iC.=^ Μχβχ— -- Μχβχ, т. e. ас== - e/χβχ, откуда ас=— e,e=— е₂е₂.

Точка а—точка касания профилей в новом положении; прямая М_ХМ₂—общая нормаль и вместе с тем линия зацепления. Угол а между общей касательной к начальным окружностям в точке с и линией зацепления называется углом зацепления. Чаще всего α=15°; в Америке применяют α— Μ¹ и α= 20°; применение последнего распространяется также и в Европе. Длина линии зацепления e=KL=длина

.дуги зацепления s=~c_2J.c_2<, откуда

Продолжительность зацепления

I пт COS а

Для рейки зубцы получают прямолиней ный профиль, перпендикулярный линии зацепления, т. к. основная окружность при этом удалена в бесконечность.

Для вычерчивания эвольвенты на основном круге и производящей прямой, начиная от точки М касания их, наносят ряд равных делений, малых сравнительно с радиусом круга. В каждой точке деления основного круга проводят к нему касательную и, откладывая на ней длину соответствующей спрямленной дуги круга, получают ряд точек эвольвенты. При черчении в большом масштабе спрямление дуг производится по одному из правил Ранкина. Часть профиля, лежащая внутри основной окружности, часто очерчивается радиально, с закруглением в 0,3 тонны при переходе к окружности впадин. Радиус этого закругления следует брать возможно больше, т. к. это дает более выгодное распределение местных напряжений при изгибе зубца р⁴]. В соответствии с работой зубцов и их нарезанием по методу обкатывания, можно рекомендовать очертание нерабочей части профиля по удлиненной циклоиде, описываемой вершиной сопряженного профиля.

Ценная особенность эвольвентных профилей заключается в том, что при раздвигании осей колес профили продолжают работать правильно, уменьшается лишь продолжительность зацепления, т. к. увеличивается угол зацепления а. Новое направление линии зацепления определится, если провести общую внутреннюю касательную к основным окружностям в их новом положении. Пользуясь этой особенностью, при сборке сближают колеса настолько, чтобы зубцы работали без зазора, не защемляясь, однако, во впадинах.

Приближенные способы очертания профилей были вызваны трудностями точного изготовления последних и сводились к тому, чтобы заменить эпициклоиды, гипоциклоиды и эвольвенты профилей дугами кругов, весьма близко подходящих к истинным профилям. Было предложено большое количество различных способов, приспособлений и приборов (одонтографов), решающих эту задачу. Исследования В. Гартмана [¹⁵] показали, однако, что 3. к. весьма чувствительны к неточностям профиля. Для передачи с чи зубцов г₁=г₂=20, при замене эвольвенты дугой круга, имеющей с ней три общие точки, оказалось, что при отступлении от теоретич. линии зацепления на 7еоо ^мм> а ^от профиля на 0,05 миллиметров, получаются колебания угловой скорости в 2,2% (от средней скорости) и ускорения в 8,8 м/с к, при w=191 об/м. и г=0,1 метров Еще сложнее обстоит дело с циклич. профилями.

С переходом к построению 3. к.,работающих при большой окружной скорости, которая доходит в настоящее время в некоторых турбинных передачах до 70 м/ск, применение приближенных профилей оказалось невозможным, и приближенные способы почти потеряли свое значение. Взамен их развились методы точного изготовления зубцов, обеспечивающие построение бесшумных передач, работающих с высокими окружными скоростями. Наилучшие результаты дает нарезание зубцов по методу обкаты вания. Заключается он в том, что нарезающий зубцы инструмент изготовляется в виде зубчатого колеса или рейки с модулем, равным модулю изготовляемого колеса. Между инструментом и заготовкой колеса воспроизводится при нарезании последнего относительное движение, соответствующее зацеплению их; начальная линия инструмента (колеса или рейки) перекатывается без скольжения по начальной окружности нарезаемого колеса. В результате на заготовке вырезаются зубцы с профилями, сопряженными профилям инструмента. Теоретически говоря, зубцы инструмента можно снабдить произвольными профилями, и они автоматически вырежут в заготовке сопряженные профили. В действительности приходится выбирать простейшие профили, могущие быть изготовленными с высокой степенью точности, которая должна сохраняться и при последующих заточках инструмента во время его работы. Поэтому особенное значение приобрели эвольвентные профили, при которых зубцы рейки имеют прямолинейное очертание. Работа нарезания зубцов по методу обкатывания производится автоматически,специальными станками.

Необходимость точного изготовления профилей окончательно разрешила вопрос о выборе между циклическим и эвольвентным зацеплением. Независимо от теоретич. недостатков и достоинств сравнительно с циклич. профилями, эвольвентные получили исключительное применение в современном машиностроении вследствие того, что: 1) 3. к. с эвольвентными профилями весьма просты в установке, 2) исходный инструмент (рейка), которым м. б. нарезаны все колеса, обладает простейшим профилем, допускающим изготовление с высокой степенью точности.

Способ нарезания зубцов оказал сильное влияние на всю постановку теории эволь-вентных профилей. Т. к. в основе изготовления их лежит инструмент, к-рый находится в зацеплении со всеми нарезаемыми при помощи его 3. к., то пришлось положить в основу теории, как исходный элемент, режущий инструмент и исследовать влияние его:

1) на характер профилей нарезаемых колес, 2) на продолжительность зацепления их и 3) на удельное скольжение как основную характеристику износа. Т. к. одним и тем же инструментом м. б. нарезаны для данного модуля все колеса, начиная от нек-рого наименьшего числа зубцов и до бесконечно большого (рейка), то в зависимости от исходного инструмента оказался также и вопрос о сменных колесах.

Набор сменных колес представляет собою ряд колес с разными чи зубцов, начиная от нек-рого наименьшего и до наибольшего, причем любая пара колес этого ряда должна находиться в правильном зацеплении. Последнее условие требует, чтобы профили колес ряда удовлетворяли одному общему закону, который для эволь-вентных колес сводится к тому, чтобы основные элементы профилей (шаг, угол зацепления и высота головки) были одинаковы у всех колес ряда.

Сменные колеса применяются весьма широко в машинах-орудиях (металлообраба тывающие станки, прядильные машины и т. д.), где по характеру работы часто требуется менять скорости вращения тех или иных частей. В наборе сменных колес выгодно назначать для наименьшего (начального) колеса возможно малое число зубцов, т. к. этому отвечает соответственное уменьшение чисел зубцов на всех остальных колесах ряда и, как следствие этого, уменьшение затрат на материал и изготовление колес. Эти соображения полностью применимы к

назначению наименьшего числа зубцов также и в парных колесах, которые работают всегда только друг с другом и не должны зацепляться ни с какими иными колесами. Наименьшее число зубцов определяется подрезанием и необходимой продолжительностью зацепления.

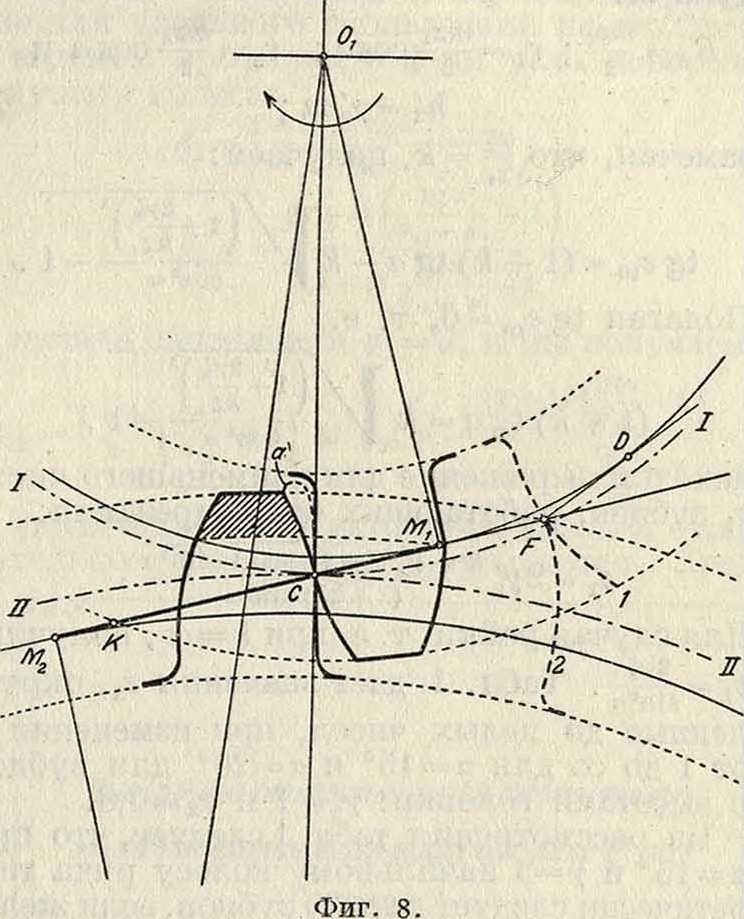
Подрезание зубцов. Если зацепление будет происходить за пределами участка М_гМ_г линии зацепления, например в F (фигура 8), то профили не будут иметь в этой точке общей нормали. Нормаль к профилю F-2 пойдет по направлению М_ХМ₂, а для профиля F-1—по DF. В результате заштрихованная часть головки колеса II будет врезаться в ножку профиля на колесе I. Характер подрезания определится удлиненной эпициклоидой а, описываемой вершиной зубца колеса II при качении его по колесу I. Наиболее сильно подрезание сказывается при зацеплении колес малого числа зубцов с рейкой.

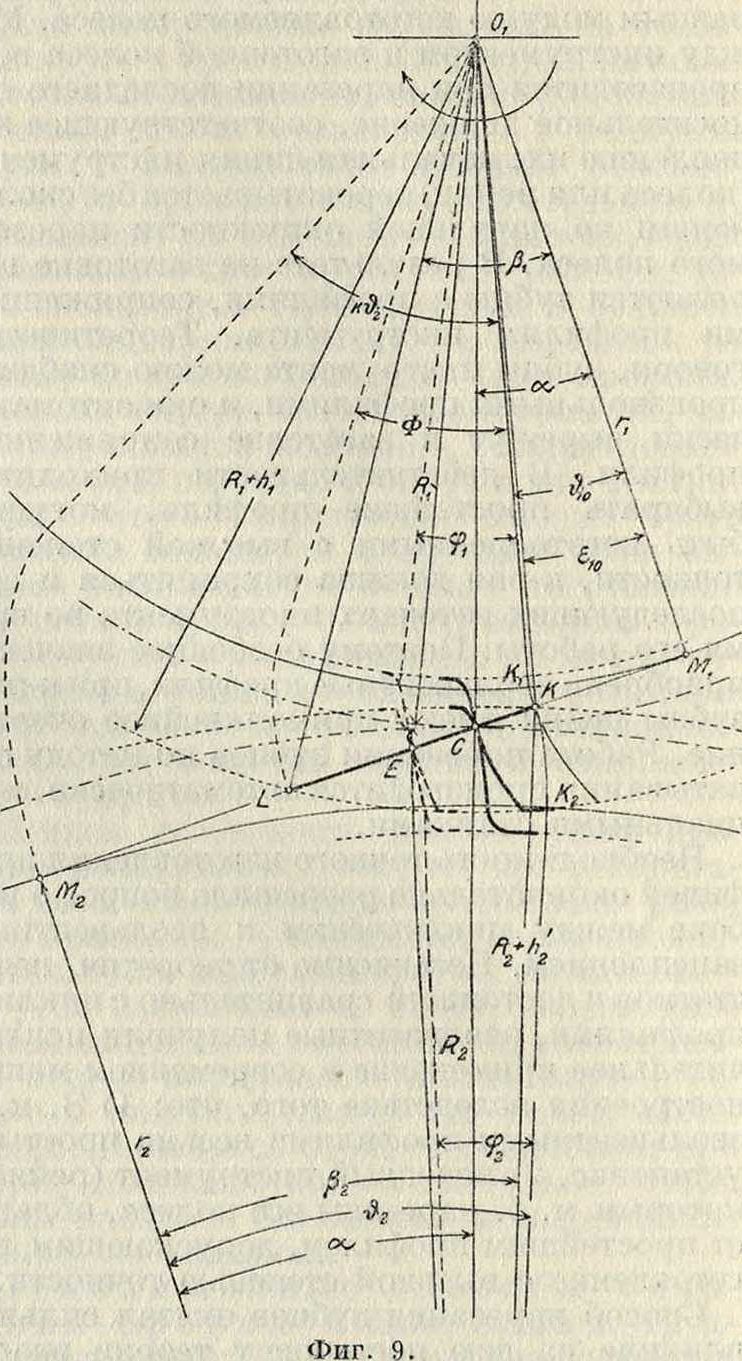
Подрезание зубца ослабляет его ножку, влечет за собой потерю части рабочего профиля и соответственное уменьшение продолжительности зацепления, а поэтому оно не должно допускаться. Для любой пары колес зацепление, во избежание подрезания, должно начинаться в точке К, лежащей между точками М_х и М₂ (фигура 9). При данном ра”-диусе г_г основной окружности отрезок М_ХК определяется углом ε₁₀:

т. э. т. VIII.

21

того, что в Америке давно уже нашел применение угол а в 20°, в особенности в тех но М_гК=М_ХМ₂ — М₂К, где

М_ХМ₂=(г, + г,) tg а и М₂К =r₂tg^₂.

Так как cos β₂=-_R, где Ιϊ₂—радиус на чальной окружности колеса 2 и ft₂—высота головки зубца на нем, то

(R*+hiy

-1.

- COS а и

‘6ιο-^τ_Γι|·6“ г, К й| cos^! (I

Выражаем важнейшие размеры через модуль т:

т-х mzo mz, mz_;

R>=-₂-‘-; П=~₂^J~ cos a ; r₂=---fe₂=y₂ m ;

замечая, что=k, получаем:

tg «ю=(1 + fc) tg Полагая tg«_ln=0, t. e.

(1 + k) tg a =

находим выражение для наименьшего числа z_x зубцов, работающих без подрезания:

₀ k + V k* + (I + 2fe) · sin^a«

^1 - (l + 2fe) sin*a

Для случая рейки, т. e. при k=со, получим:

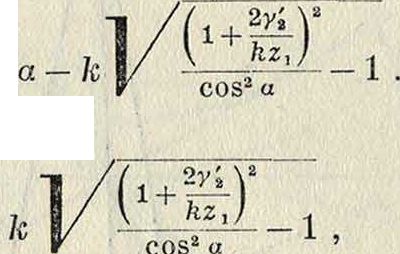
2, =

2 7а

Таблица 1 дает значения z_u округ ленные до целых чисел, при изменении к от 1 до со для а=15° и α= 20° для зубцов с высотами головки: γ,=ί и у₂=0,8.

Из рассмотрения табл. 1 следует, что при а=15° и у=1 начальному колесу ряда теоретически следует дать 30 зубцов, если желательно совершенно исключить подрезание. Практически при г,=28 подрезание почти исключается, т. к. значение к в наборе сменных колес обычно не достигает 10. В металлообрабатывающих станках наименьшему колесу дается 20, 22, а чаще всего 24 зубца. Т. к. в этом случае к не превосходит 5, то при 24 зубцах правильная работа колес получится при значениях к=1 А 2 и работа с

Таблица 1. — Мин и м а л ь н ы о. ч и ела з у б ц о а= 15 и 20° для к=1 -т- со.

шестерни при

^УгльР^		1	2	3	4	5	6	7	8	9	10	OO
a=15°	72—1	21	24	26	27	27	28	28	28	28	29	30
	72=0,8	17	20	21	22	22	23	23	23	23	23	24
a=20°	72=1	13	14	15	16	16	16	16	16	17	17	17
	to II о 05	u	u	12	13 13		13	13	13	14	14	14

нек-рым подрезанием—при к=2-г δ. При начальном колесе с 20 зубцами во всех случаях работа связана с подрезанием. Увеличение угла а до 20° значительно уменьшает значение величины г, для начального колеса, такое же влияние оказывает уменьшение высоты головки при неизменном а. Уменьшение числа % и связанное с ним уменьшение размеров колес является главной причиной случаях, где требование компактности передачи является основным (автомобили и тому подобное.). Дальнейшее стремление к уменьшению ζ_χповело к применению укороченных зубцов. с высотой головки h= ==0,8 тонн При выработке стандарта на зубчатые колеса Германия приняла a=20° и h=m; в Голландии эти величины установлены: «=20° и h==0,8 т.

Продол ж и т ель-ιι о с т ь зацеплен и я определена выше ф-лой:

е а —

лm cos a

Длина е линии зацепления равна KL (фигура 9). KL=М_ХМ₂ - (М_ХК + + LM_t); но MjM₂=и (1 + к) tg α; Μ_λΚ =

- r_x (1 + к) tg a - r₂ tg β₂: LM₂=r₁(l + fc)tg a-

- r_x tg β_χ, откуда

e=Η [(tg + ^rr tg βύ - (1 + «) tg «] ·

Продолжительность зацепления

σ=~ [(tg /?! + 7c tg ft,) - (1 + fc) tg a],

при чем

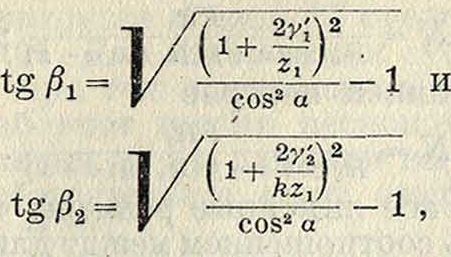
где у[ и у₂—высоты головок на колесах, выраженные в отношениях: у[=и у₂=;

σ зависит от %, к, а, у[ и у₂. Для случая рейки и колеса соответствующую формулу следует вывести самостоятельно. Предельный случай, соответствующий зацеплению рейки с рейкой, дает: 1) для а= 15° и у=1, α= 2,54; 2) для α= 20° и=1,<т= 1,98. Кривые, данные на фигуре 10, выражают зависимость σ от ζ_χ при разных значениях к и а.

Относительное с к о л ь Hi е н и е представляет собою главную характеристику износа зубцов, зависящую от формы и элементов профиля. Рассматривая зубцы в начале зацепления (фигура 9), отмечаем, что точка ведущего профиля, находящаяся в этот момент в зацеплении, определяется углом #₁₀=tg е₁₍₁, а соответствующая точка ведомого профиля, то есть его вершина, углом &₂. Угол ψ_χ поворота ведущего колеса будем отсчитывать от радиуса 0_±Κχ, а угол <р₂ поворота ведомого колеса—от радиуса 0₂К₂. Если профили будут касаться один другого в некоторой точке Е на линии зацепления, то

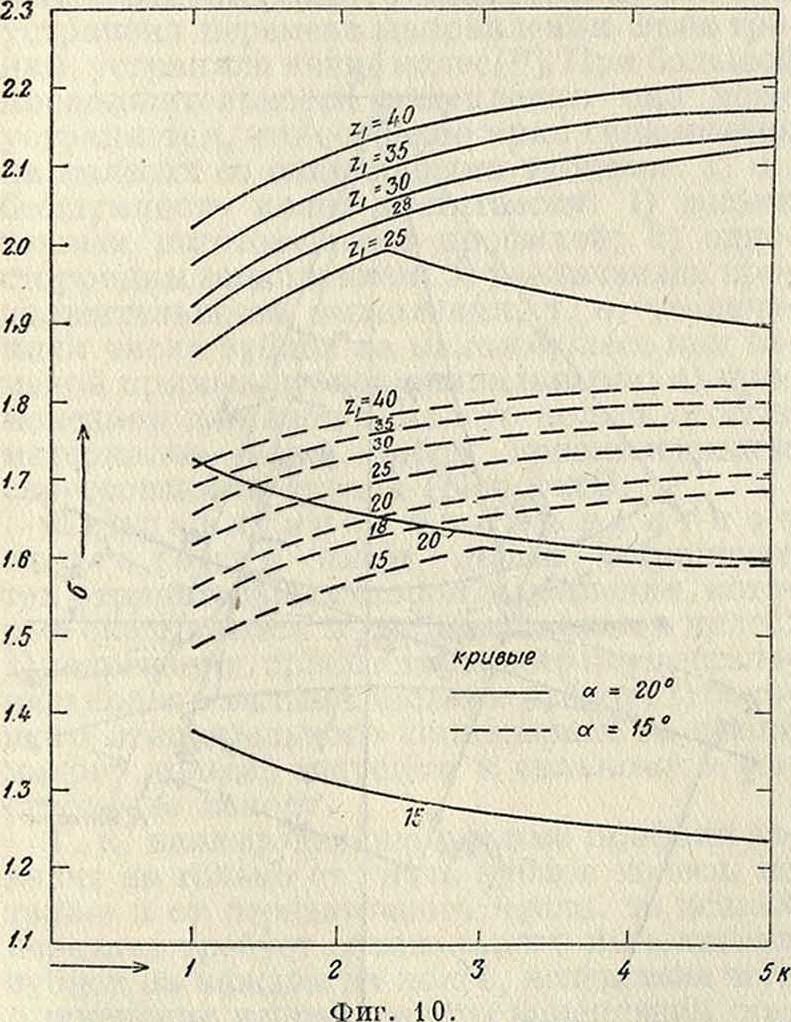
положение соответствующей точки на ведущей эвольвенте будет определяться углом &₁₀ + <Ρι, а на ведомой—углом #₂ — φ₂; соответствующие длины дуг эвольвенты:

К=2 ^Г1 (#10 + Pi)² И λ₂=I Г₂ (#₂ - φ₂)

Переходя к величине (/относительного скольжения, получим две следующие формулы.

1) Для ведущего профиля

~ 1^-2 _ О 2 — 9-2 -|

cul ~ „+?>, ’

2) для ведомого (т. К. Г_х d<p_x=—Г₂ άφ₂)

“ >+9>ι _л

- <tz

92 =у

Из фигура 9 следует:

#₂=H^g“-x·

Подставляя это значение &₂ в ф-лы для д_г и д₂ и замечая, что <р_х=к<р₂, по выполнении всех действий получим следующее выражение для удельного скольжения на ведущем и ведомом профилях в ф-ии угла поворота ведущего колеса:

а ₌ !+Л (.JsiL_ _ i) -9* ^k Ui+fi 7 ’

a 2=-

^{(h + 1)} Si’.Wr¹

В начале зацепления <р₁=0, и мы получаем:

1 + k /tg α _л

9ю=Т^- (»“ ~ ¹) “ 9го =

№ + 1)

. tga

И.

С увеличением передаточного числа к относительное скольжение уменьшается. Угол

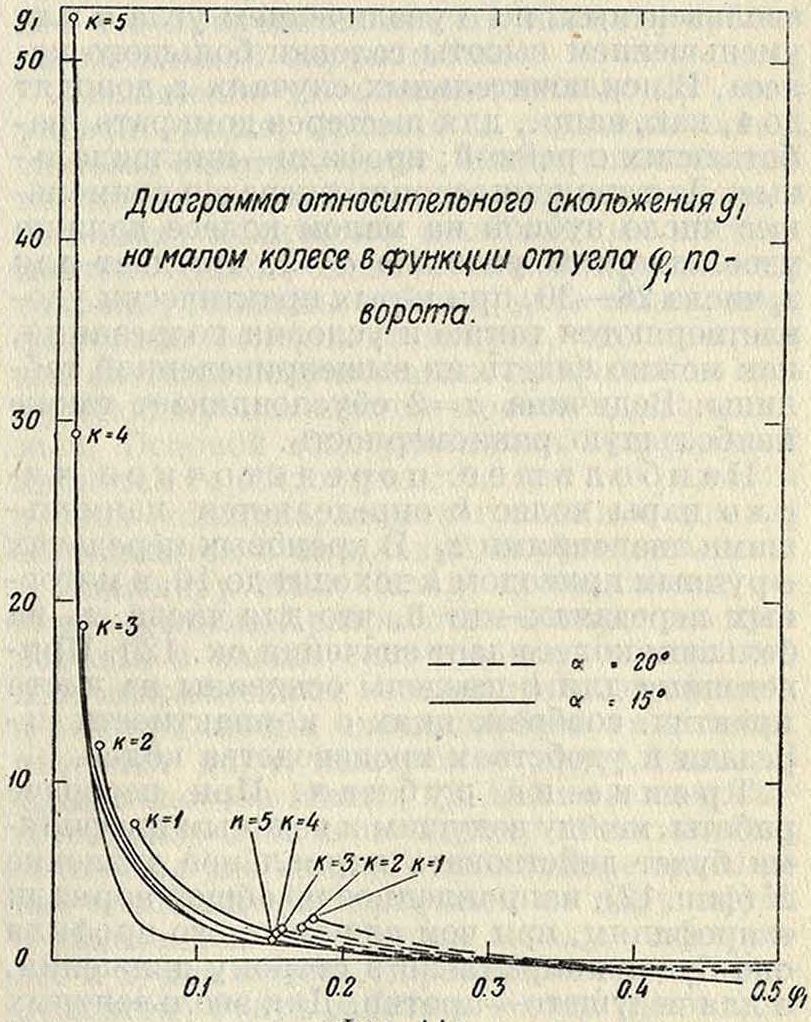
Диаграмма относительного скольжения д, на малом колесе е функции от угла ^поворота.

" о.г о.з

Фигура На.

<р_х изменяется за время зацепления одной пары зубцов от <р_х=0 до Ф=~ а. Если #₁₀=0,

то есть пояска ведущего профиля вступает в зацепление той точкой эвольвенты, которая лежит на основном круге, то д₁₀=со, чему будет соответствовать весьма сильный износ ножки. Такого случая следует избегать. Диаграмма (фигура 11а) дает представление об относительном скольжении д_г для передачи при г_х=28 и к=1, 2, 3, 4, 5. Определяющее значение для передачи имеет величина д₁₀относительного скольжения на профиле ножки малого колеса. Диаграмма (фигура 116) дает зависимость этой величины от к для шестерни с z_x=28. При постоянном угле а величина д₁ зависит только от #ι₀+9>ι, то есть в конечном счете от #₁₀.

Наименьшее ч и с л о з у б ц о в, которое можно назначить на малом колесе передачи или набора сменных колес, зависит от всех исследованных выше факторов, то есть от подрезания, продолжительности зацепления и относительного скольжения, и определяется характером работы передачи. Для передач, работающих с малой окружной скоростью, допускается а < 2. Износ при малых скоростях, особенно в передачах, работающих с перерывами, также те-

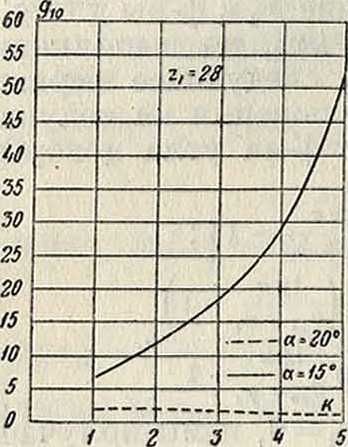
Фигура 116.

ряетсвое значение. Поэтому для колес, зубцы которых изготовляются отливкой и обработке не подвергаются, наименьшее z_x доводят в лебедках до 10—11, при условии применения циклоидальных профилей или эвольвентных, но с увеличением угла а или уменьшением высоты головки большого колеса. В исключительных случаях z_x доводят до 4, как, например, для шестерен домкрата, работающих с рейкой; профили—циклоидальные. Для трансмиссионных передач наименьшее число зубцов на малом колесе должно удовлетворять условию <г=2, что дает для z_x числа 28—30, при которых практически удовлетворяются также и условия подрезания, как можно видеть из вышеприведенной таблицы. Величина σ=2 обусловливает также наибольшую равномерность.

Наибольшее передаточное число пары колес к определяется наименьшими значениями г_х. В крановых передачах с ручным приводом к доходит до 10, в моторных передачах—до 6, что для числа г₂ на большом колесе дает значения ок. 120. Приведенные для к пределы основаны на чисто практич. соображениях о компактности передачи и удобствах производства колес.

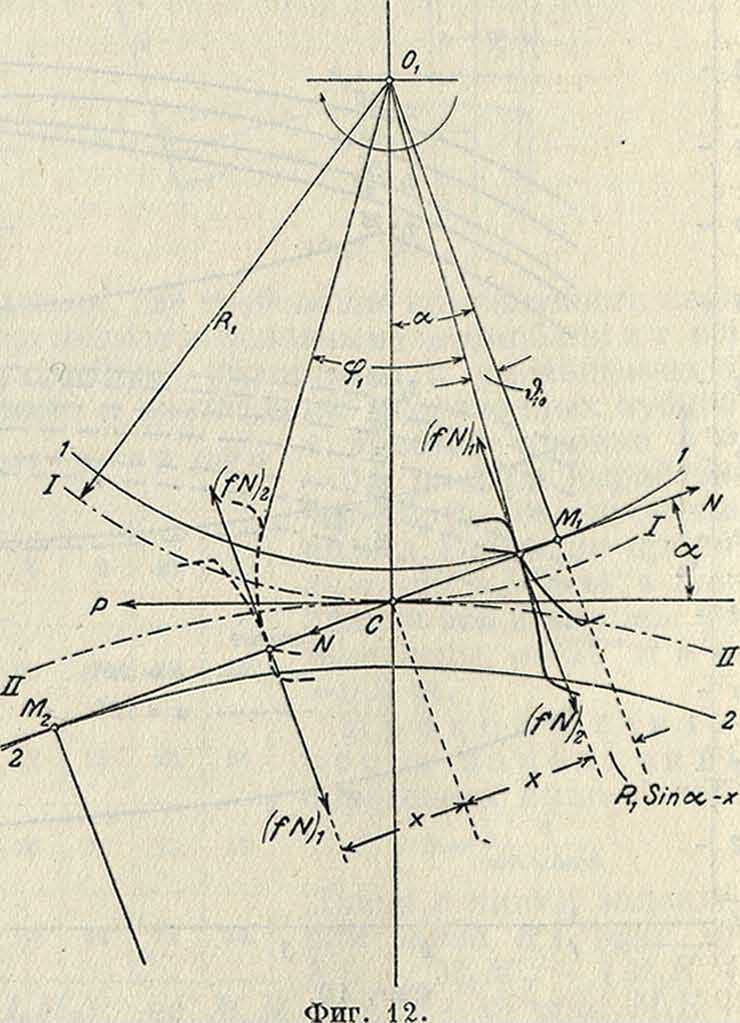
Трение на зубцах. При передаче работы, между ведущим и ведомым профилями будет действовать нормальное давление N (фигура 12), направленное по общей нормали к профилям, причем для ведомого профиля оно будет направлено в сторону движения, а для ведущего—против. Для эвольвентных профилей N будет иметь постоянное направление по касательной к основным кругам обоих колес. При отсутствии трения моменты обоих колес М_х =Nr_t и M₂=JVr₂, так

^Гг— ** Сила трения fN, в соответствии с направлением скорости скольжения, будет направлена на ведущем профиле: 1) к основанию зубца—при работе перед линией центров и 2) к вершине зубца—за линией центров. Перемена направления силы трения происходит в точке С. Предполагая движение установившимся, из условий равновесия ведущего колеса определяем нормальное давление следующим образом. что

Ms _ 2 _

м I г.

1) Перед линией центров

N =

PRi

Л, COS α + (Н, sin a - ж) ’

2) за линией центров

Л^т=-

PR,

Я, COS а - (Я, sin а + X)

Выражая все линейные размеры через т и пользуясь соотношением между длиной х линии зацепления и углом поворота

X=Гц [tg а — (0_1О + ?>!>],

получим для N следующее выражение, справедливое для работы профилей как перед линией центров, так и за ней:

)У =________ ^р..

COS α [1 - 1 (fi_l0 + 9>,)]

Отсюда заключаем, что нормальное давление и сила трения суть ф-ии угла <р_х поворота ведущего колеса.

Коэффициент полезного действия η пары 3. к. вычисляют обычно р в предположении, что N= _cos~, то есть пренебрегают влияпием трения на величину N. В результате получается выражение

V=1 ~ⁿt (“ + ”) К + σ|- а + 1), или, приближенно,

ч-¹-»/(-*-+у;,

где ζ_χ и ζ₂—числа зубцов, а_х и <т₂—продолжительность зацепления перед и за линией центров, σ—полная продолжительность зацепления; коэфф-т трения /= 0,1 -^0,25.

Опытом установлены следующие средние значения η, включая трение в опорах:

1) для новых литых и необработанных зубцов—от 0,85 до 0,88; 2) для обработанных— 0,92; 3) для очень хорошо обработанных— 0,95. Опыты Каммерера и Кранца с трамвайными 3. к. показали, что η зависит от смазки и ее сорта, нагрузки на зубцы и ок-

ружной скорости. Для новых колес при нормальной нагрузке и жидкой смазке η доходило до 0,98. Для изношенных зубцов η понижается при тех же условиях до 0,87, и колеса работают весьма неспокойно. Подробные данные об г? и влиянии на него различных обстоятельств дают американские опыты [²¹, ²⁵, ²⁶].

Трение на зубцах оказывает влияние на равномерность вращения колес. Если ведущий момент Л?! постоянен, то при переменном моменте трения ведомый момент не м. б. постоянным. Особенно сильное влияние оказывает при этом то обстоятельство, что сила трения, а значит и полная реакция на ведущий зубец, меняют свое направление в точке С. Все это сказывается гл. обр. в звуковых явлениях: колеса шумят или ревут при работе. Опыты показали, что колеса, зубцы которых после обработки были закалены, работают с шумом вследствие искажения профилей при закалке; если зубцы после закалки подвергались шлифовке, то колеса работают без шума. При профилях, весьма точно и тщательно изготовленных, колеса давали вместо шума музыкальный тон, высота которого пропорциональна произведению числа оборотов колеса на число его зубцов, то есть числу зацеплений зубцов в минуту. Сила звука зависит от нагрузки; при увеличении нагрузки она увеличивается, при уменьшении—уменьшается; при холостом ходе она равна нулю, пения не слышно. Применение одностороннего зацепления, в к-ром устранена перемена направления силы тре^ ния, устраняло пение колес [^а?]. При большой продолжительности зацепления оно тоже устраняется, что особенно ярко сказывается на колесах со спиральными зубцами. Т. о., бесшумность колес достигается: 1) весьма точным изготовлением профилей; 2) односторонним зацеплением; 3) увеличением продолжительности зацепления, то есть увеличением числа зубцов на малом колесе или заменой прямых зубцов спиральными; 4) применением для зубцов малого колеса особых материалов—кожи, фибры, просмоленных и спрессованных тканей (Novotext).

Исправленное эвольвентное зацепление имеет целью устранение тех отрицательных сторон зацепления, которые сказываются в системе сменных колес:

1) подрезания, препятствующего осуществлению колес с малыми чи зубцов; 2) большого относительного скольжения на ножке малого колеса, ведущего к сильному и быстрому ее износу.

Т. к. наивыгоднейшая форма профиля зависит не только от числа зубцов колеса, но также и от передаточного числа, то всякая передача требует специального выполнения зубцов на каждом из колес, вследствие чего применение исправленного зацепления становится в зависимость от режущего инструмента и методов обработки зубцов. Улучшение характера зацепления сводится в конце концов к увеличению эвольвентной части зубцов малого колеса и м. б. достигнуто:

1) увеличением высоты головки за счет сокращения ножки при неизменном угле; 2) увеличением эвольвентной части ножки путем увеличения угла а при неизменной вы соте головки; 3) одновременным увеличением высоты головки и угла а при очень малом числе зубцов.

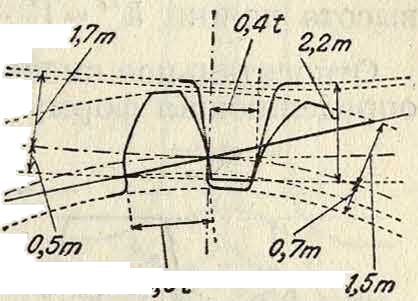
Примером исправления профиля по первому способу являются зубцы, применяемые с 1901 г. германской фирмой AEG (Всеобщая компания электричества) для передач от электромоторов (фигура 13). Высота головки этих зубцов на малом колесе увеличена на 0,5 т, угол а=15°, общая высота зубцов 2,2 т; остальные размеры указаны на фигуре 13. Исправление это позволяет брать на малом колесе 14 зубцов, но не является универсальным, т. к. ~ дает хорошее зацепление только для передаточных чисел от Здо5. Обобщение его на любые переда- Фигура 13.

точные числа потребовало бы установления шкалы размеров для высоты головок в зависимости от числа зубцов на колесах, составляющих передачу; в соответствии с этим осложнилась бы обработка зубцов, вследствие необходимости большого количества инструментов, тем более что приходится менять толщину зубцов на начальной окружности.

Увеличение угла зацепления до 20°, как указано выше, привело к созданию новой системы сменных колес. Назначение же для каждой пары особого угла приводит снова к большому количеству необходимых инструментов. Одновременное изменение высоты головки, толщины зубца и угла зацепления настолько осложняет вопрос, что построение системы исправленных профилей по этому способу становится просто невыполнимым. Основой всех указанных затруднений является то обстоятельство, что все размеры зубцов (толщина, высота головки и ножки) связываются с начальной окружностью.

Инженеру Мааг (Maag) принадлежит заслуга детальной разработки и широкого проведения в жизнь системы получивших его имя исправленных эвольвентных профилей, которые при любых числах зубцов на колесах передачи дают наилучшее зацепление. В основе способа Маага, предполагающего изготовление зубцов по методу обкатывания, заложены две идеи:1) правильное зацепление эвольвентных профилей не нарушается с изменением расстояния между осями колес и 2) два колеса, нарезанные одним инструментом, будут работать всегда правильно друг с другом. Исходным инструментом выбрана рейка с углом зацепления а₀=15° и шагом i₀=jtm. Толщина зубца по средней прямой, которая называется модульной

„ to пт т-»

прямой, равна ₂=—. Высота голов-

ки равна высоте ножки=т (фигура 14). Т. к. все точки рейки в прямолинейном ее движении имеют одинаковые скорости, то за начальную прямую мояшо взять любую прямую, параллельную модульной. Другими словами, можно отодвинуть рейку от центра колеса на величину ж, называемую смещением и выражаемую через модуль

ж=ξηι. Смещение считается положительным, если модульная прямая отодвигается от центра обрабатываемого колеса, и отрицательным, если последняя придвигается к центру. Начальной окружности, которая в точке С касается начальной прямой рейки, дается название модульной окружности, для к-рой R₀=™^z-; но ней измеряется толщина зубца, и от нее отсчитываются высоты головки и ножки зубца на колесе. На фигуре 14

высота ножки h"=Q — | j т.

Относительное смещение ξ есть величина, определяющая форму зуба. Полагая зацеп-

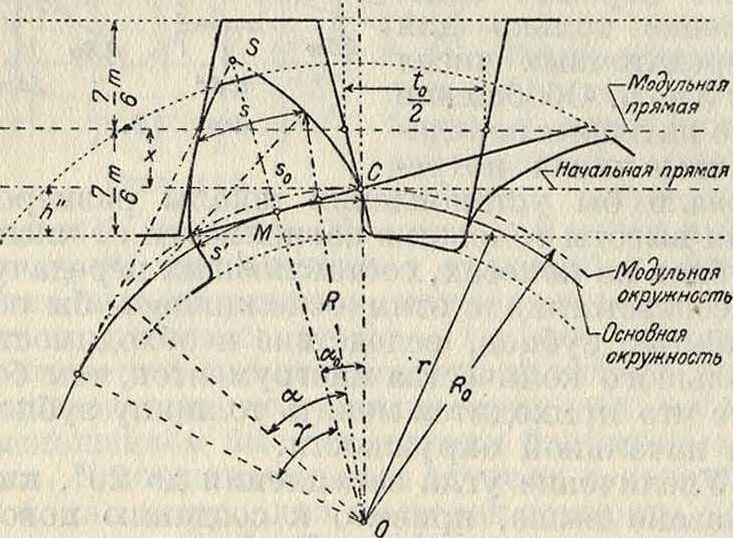
Фигура 14.

ление рейки с колесом без зазора, определим толщину 5₀ зубца на колесе по модульной окружности:

+ ^2jtg «0=2 + ξtg α₀) т,

то есть толщина s₀ определяется величиной сме-щения. На фигуре 14 изображен такой зубец, и пунктиром профили его продолжены до пересечения в точке S. Толщина зубца на любой окружности радиуса 11

s=2 [(tg γ - γ) - (tg a — a)] R ;

Т» тл т. к. г=R cos а И Г=K₀COS «₀=— COS «о, то 5=[(tg γ - γ) - (tg α - a)] ^~^α-⁰ mz.

Толщина зубца по модульной окруясности по этой общей формуле определится как

»о=[(tg У-У)~ (tg «„ - «о)] mz. Сопоставляя два выражения для s₀, находим:

2tg а„

tg y-y=

^ξ + 2Ϊ

tg «о - «о где угол γ определяет толщину идеального зубца на основной окружностиs_x= 2г (tgу—у). Полагая, что рейкой нарезаются два колеса, которые составят передачу, причем зубцы будут работать без зазора и иметь по начальным, модульным, окружностям передачи толщины Sj и s₂, имеем:

s_L + s₂=t=t₀ —;,

где a—новый угол зацепления. Применяя к каждому колесу выражение, приведенное выше для s в ф-ии tg γ — γ, находим:

(tg Ух- Ух) 2χ+ (tg У у») г₂- (tg a- α)(Ζχ+z₂)=π. Подставляя соответствующие значения для

tg У — У, находим выражение для определения угла а зацепления нашей пары колес:

_ 2tg

Ζι + z₂

tg а-

- (Si + Si) + tg a₀ — a₀

где ξχ и ξ₂—смещения рейки при нарезании 1-го и 2-го колес передачи, ζ_τ и ζ₂—числа зубцов на них, а₀=15°. Изменение расстояния между центрами колес где η =

y=Rx (~°~° -1)

^{J 1} COSa

Xi 2« /(

= — ^m (i

. /COSa₀ _ - _

C0Sa )

R„

/cos a. _ _

VCOSa ^_

COS a, COS a

= η -m.

относительное сме щение центров колес. Каждому а, то есть паре значений ξχ и f₂> соответствует свое η. Для упрощения вычислений при нахождении угла а служит вспомогательная таблица значений функции tg а — а [¹⁴]. При нарезании рейкой зубцов на колесах допускается нек-рое подрезание их, но так, чтобы при этом совершенно не затрагивался рабочий участок эвольвенты на профиле.

В основу определения величин ξ положены два требования: 1) зубцы колес должны работать без подрезания, 2) толщина зубцов по окружностям, отделяющим подрезанную рейкой часть профиля от неподрезанной, должен быть на обоих колесах одинаковой. Результаты вычислений сведены в диаграмму [^м]. изображающую ξ в функции от ζ.

Колесами Маага могут осуществляться пе редачи ОТ ³/₃ ДО ³/со и от

⁵⁰,/оо. Для

шестерен с числом зубцов свыше 50 оказывается, что наилучшие результаты дают обыкновенные колёса сменного ряда с углом зацепления α= 15°. Колеса Маага не удовлетворяют условиям сменности и пригодны только для парных передач.

Позднейшие исследования показывают однако, что, исходя из рейки как основного инструмента, можно нарезать системы сменных колес, отличные от современных. При построении этих систем удобнее исходить из основных кругов, относя к ним модуль и шаг зацепления. Определяющими условия^ ми являются: 1) беззазорная работа зубцов, 2) недопустимость подрезания, 3) недопустимость заострения зубцов, 4) минимальная продолжительность зацепления для малых колес набора. Вообще следует отметить, что отнесение модуля и шага зацепления к основным окружностям весьма упрощает общее геометрическое исследование и характеристику также и существующих систем сменных колес.

2. Расчет и конструкция цилиндрических

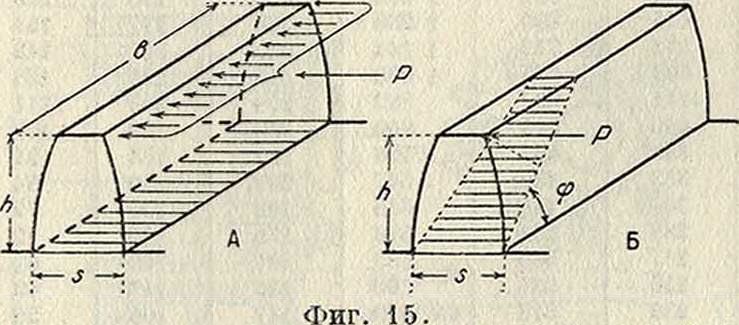
3. к. Расчет зубцов ведется обычно в следующих предположениях: 1) окружное усилие Р, изгибающее зубец, действует на вершине зубца и дает в опасном сечении изгибающий момент M_u=Ph (фигура 15, А);

2) толщина s зубца у основанйя его прини-

о t тст мается для простоты равной ,то есть равной толщине зубца по начальной окружности. Тогда из ур-ия прочности зубца по-

лучаем: а[_к=- ^, где о—длина зубца. В гру-

бых колесах возможно действие силы Р на угол зубца (фигура 15, Б), что дает:

Ph cos φ=—^,1ί - a”, т. e. σ=~ sin 2<ρ.

^r 6S1IKP " ’ “ s“ ^r

Опасное сечение определяется углом φ =

3 р

= 45°, при котором σί=-^-. Полагая σ;₍_== σ;/.= σ_Μ, приходим к условию равнопроч-ности зубца: b=2h; при h — 0,it з= 2,167 тонн получаем 6=1,4 <=4,334 т, то есть при грубых" колесах, когда не исключена возможность действия силы Р на угол зубца, бесполезно брать длину зубца больше 1,4 <, т. к. это не повышает его прочности. Обычно в этих случаях принимают b=2t^6m.

Переходя к установлению расчетных уравнений, полагаем b=yt=ц>лт=у>т; в дальнейшем, при выводе ф-л для перехода на ем,

будем вводить везде —, где т выражено В миллиметров; тогда Ь=— СМ, И·—-гг:— сантиметров и β

ίο

0.5 пт нГ

см;

ΤΪ 6S² 7

^ ~ "б К ^{С и}- ~ откуда

ipm · 0,25 я²т“ 6 · 2,167 «1-100

/с_гл=0,001883 т²у>к.,

ш

= 23-

Р

Т. к. вращающий момент М=PR кгсм =

= Р _2о кгсм, то

„„ ³ /" Λί

^W=22F Ж‘

Переходя к мощности N_Jp и числу об/м. и,

найдем _

При расчете различают два типа 3. к.: 1) силовые колеса и 2) рабочие колеса. Первые работают при весьма малых скоростях и имеют целью не длительную передачу работы, а гл. обр. передачу усилий, иногда весьма больших. Типичный пример таких колес дают передачи в кранах с ручным приводом. Основанием для расчета зубцов силовых колес являются исключительно соображения прочности, то есть выбор допускаемого напряжения /с₁₍., которое определяется лишь материалом. В противоположность силовым, рабочие колеса имеют главной своей целью б. или м. продолжительную передачу работы. В типичных случаях они работают при весьма значительных скоростях. При расчете их приходится принимать во внимание не только прочность, но также износ и нагревание зубцов вследствие трения. ^Последние обстоятельства приводят к необходимости увеличивать длину Ь=у>т зубца, а также уменьшать значения /с_м. при возрастании окружной скорости. Для средних скоростей и усилий y>=9-f-12. Сюда относятся, между прочим, 3. к. в металлообрабатывающих станках, для которых принимают обычно у>= 10. Для колес, передающих большие усилия при большой скорости, у=13-|~16.

Сопоставляя данные лучших герм, з-дов, а также соображения разных авторов (Бах, Рело), Гённике (G. Honnicke) [¹⁶] установил,

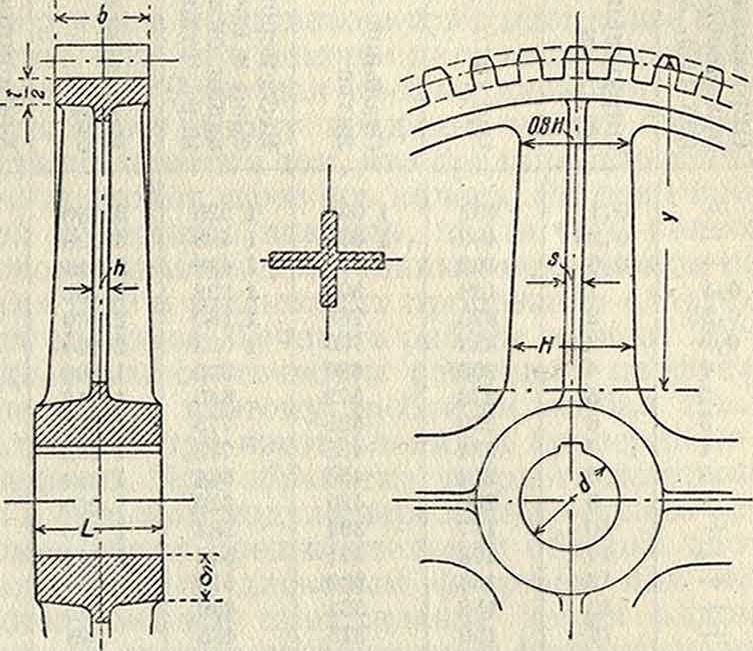
Фигура 16.

что все их можно объединить в одном законе: К_и. ⁼¹^+% > ^гДе ^ки. (выраженное в килограммах/см²)—

допускаемое напряжение для зубцов рабочих колес, /<_м.—допускаемое напряжение для зубцов силовых колес и v—скорость на начальной окружности в м/ск. Таблица 2 дает значения К„. для разных материалов, применяемых при изготовления 3. к.

Напряжения, соответствующие v—4 м/ск, должны применяться для расчета силовых колес. Расчет приходится вести методом последовательных приближений, задаваясь вначале произвольной скоростью v; для облегчения и ускорения расчета пользуются

вспомогательными таблицами и номограммами. Строго выработанного метода расчета зубцов не имеется, а поэтому приводимый способ не является единственным.

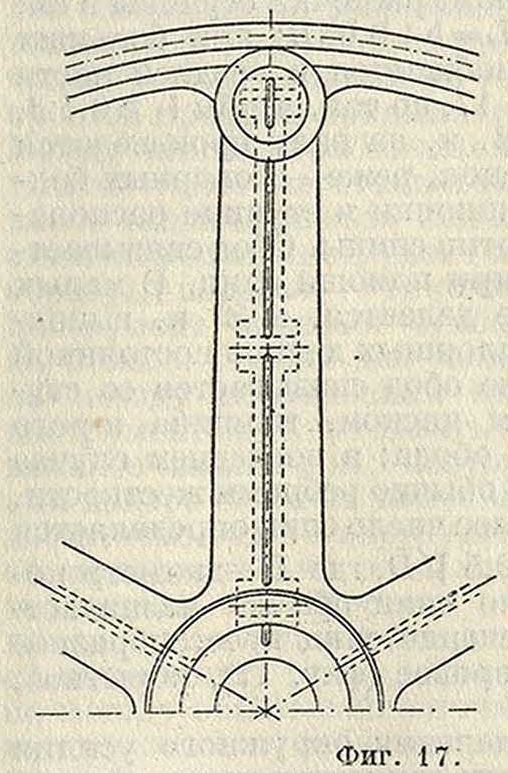
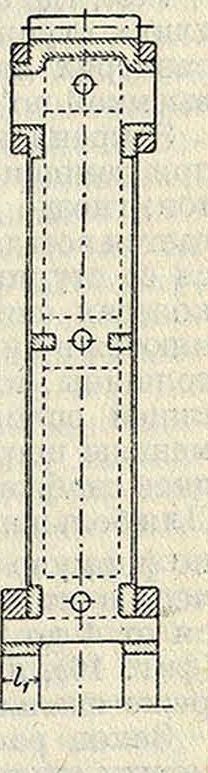
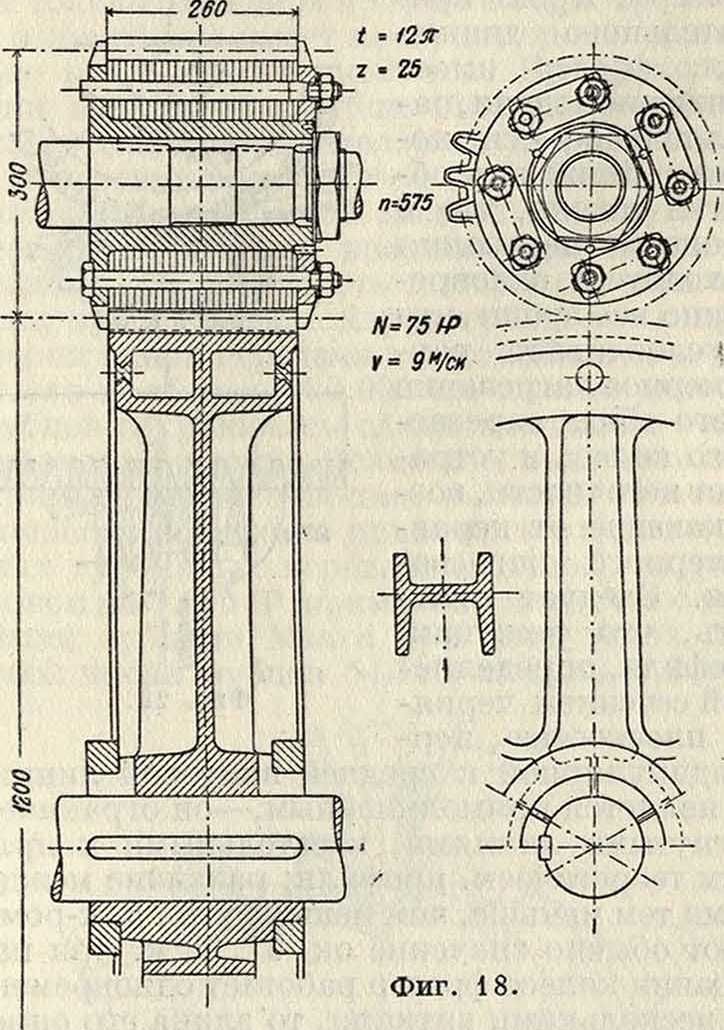
Конструкция цилиндр, колес и расчет деталей (фигура 16, 17 и 18). Обод делается толщиной от 0,5 до 0,С<; для

Окружная скорость при необработ. зубцах (ν), м/ск	Окружная спорость (V), М/СП	10 ku Допускаемые напряжения Ки=— в килограммах/см2 для рабочих колес с обработанными зубцами. Значения напряжений при v=i м[ск применяются для силовых колес
		Чугун	Стальное литье	Бессемеровская и кованая сим.-март. сталь	Никелевая сталь	Хромо-никелевая сталь, колеса закалены в масле	Б1Х0НЗ а	Фосфористая! бронза	Дельта- металл	Кожа	Бук	a о §
	0,1	492	1 030	1 525	3 100	4 100	656	885	1 312	410	295	164
—	0,25	480	1 000	1 485	3 020	4 000	610	864	1 280	400	288	160
—	0,5	462	970	1 430	2 910	3 850	615	830	1 230	385	277	154
0,1	1	428	900	1 328	2 700	3 570	572	772	1 144	357	257	143
0,25	2	375	768	1 160	2 360	3 125	500	675	1 000	313	225	125
0,5	3	333	700	1 032	2 100	2 780	414	60Э	889	278	200	111
1	4	300	630	930	1 880	2 500	400	540	800	250	180	100
2	5	273	572	845	1 717	2 270	363	491	726	227	164	91
3	6	259	525	775	1 575	2 085	333	450	667	209	150	84
4	7	231	485	715	1 452	1 923	307	416	615	192	138	77
5	8	214	450	664	1 350	1 785	288	386	576	179	129	72
6	9	200	420	620	1 260	1 665	267	360	535	167	120	67
—	10	187	394	581	1 180	1 563	250	337	500	156	113	63
—	11	176	371	546	1 111	1 470	235	318	470	147	106	59
—	12	166	350	516	1 050	1 388	222	300	445	133	100	56
—	13	158	331	490	995	1 315	213	284	426	132	95	53
—	14	150	315	405	945	1 250	200	270	400	125	90	50
—	15	143	300	443	903	1 190	190	257	380	119	86	48
—	16	136	286	422	860	1 135	182	245	364	114	82	46
—	17	130	274	404	S22	1 090	174	234	349	109	78	44
—	18	125	262	387	787	1 042	166	225	333	104	75	42
—	19	120	256	372	756	1 000	160	216	320	100	72	40
—	20	115	242	357	729	962	154	207	308	96	69	39
—	21	111	233	344	700	926	148	200	296	93	66	38
—	22	107	225	332	675	893	143	193	286	89	64	36
—	23	103	217	320	661	862	138	186	277	86	62	35
—	24	хоо	210	310	630	833	133	180	267	83	60	34
—	25	97	203	300	610	806	129	174	258	81	58	32
—	26	94	197	290	591	782	125	169	250	78	56	31
—	27	91	191	282	573	758	121	164	243	76	54	30
—	28	88	185	273	556	735	117	159	234	74	53	29
—	29	86	180	265	540	714	114	154	228	71	51	28
—	30	83	175	258	525	695	111	150	223	70	50	27

увеличения жесткости обод снабжают одним или двумя ребрами. Толщину стенок <5 ступицы для чугунных колес берут равной 0,4d+l см; для стального литья <5=0,Зс2+ + 1 см, где d—диам. расточки ступицы в см; длина ступицы L=b+0,05R; при больших размерах она снабжается в средней части выемкой по фигура 17, но так, чтобы 1_г 0,5 d.

Закрепление 3. к. на валу производится при помощи шпонок, реже—стопорных болтов; гнездо для шпонки в ступице располагается всегда против спицы. Обод связывается со ступицей при помощи спиц. В малых колесах спиц не делается, и 3. к. выполняются в виде сплошных дисков постоянной толщины, или же обод связывается со ступицей сплошным диском, толщина которого меньше ширины обода; в последнем случае диск снабжается обычно ребрами жесткости. Для больших колес число спиц определяется по формуле г=0,5 Уb, где Ώ—диаметр колеса в см. Число спиц обычно назначается от 4 до 8. Сечение спиц крестообразное (фигура 16), двутавровое (фигура 17), корытное, реже овальное.

Закон распределения окружного усилия между отдельными спицами весьма сложен; поэтому расчет спиц ведется приближенно, в предположении, что в работе участвует одновременно ¹/₄ общего числа спиц. Обыкновенно в расчет принимаются только ребра, расположенные в плоскости вращения колеса. Ширина ребра в опасном сечении—II, толщина fissO,2 Я. Рассматривая спицу как балку, защемленную в сечении у втулки колеса и нагруженную сосредоточенной силой Р на начальной окружности, получают: ___

_ I. IP. _тг ³ А120 Ру

^ру=4^г-so-^,г«·,^откУ^{дан =} V TftA^-

Для чугунных колес /с_!(. =300 килограмм/см². Ширину спицы у обода берут равной 0,8Я. Ребра, перпендикулярные плоскости колеса, являются ребрами жесткости и служат для связи обода со ступицей. Ширина их определяется размерами b и L, а толщина s делается равной h. Если чугун не удовлетворяет условиям работы, то большое колесо передачи изготовляют в виде стальной отливки, а малое—из кованой стали, причем зубцы последнего часто закаливают для увеличения срока его службы. В специальных случаях малые колеса изготовляют из никелевой или хромоникелевой стали, подвергают термич. обработке и шлифовке,—тогда обод большого колеса готовится из кованой стали. Для бесшумных передач малое колесо изготовляется из кожи (фигура 18), фибры, за последние годы—из тканей, спрессованных в нагретом состоянии с искусственной смолой (Novotext) [⁸⁴]. Для бесшумности иногда делают обод колеса полым и заливают его цементом или свинцом. С той же целью применяют деревянные зубцы, которыми снабжается обыкновенно большое колесо передачи, чтобы избежать сильного износа деревянных зубцов. Обработка зубцов чугунной шестерни содействует даль нейшему уменьшению износа. Толщина деревянных зубцов 0,6ί; толщина обода для них от 1 до 1,2ί.

При невозможности надевать колесо с торца вала (например в трамвайных передачах) или затруднительности его отливки вследствие большихразмеров колесо изготовляется разъемным (фигура 17). Разъем обыкновенно делается по спицам, и части колеса соединяются между собой болтами или стяжными кольцами.” Число зубцов колеса в этом случае

должен быть кратным числа спиц. Для обеспечения постоянной смазки передача заключается в кожух и работает в масле. При окружных скоростях больше 9 м/с к, вследствие действия центробежной силы масло сбрасывается с зубцов; поэтому при больших скоростях масло подается особым насосом и вбрызгивается между зубцами в месте зацепления. Смазка действует также в качестве охладителя и глушителя шума зубцов.

3. Изготовление цилиндрических 3. к. Изготовление производится двумя методами: 1) по методу копирования и 2) по методу обкатывания. В основе первого, более старого метода, который молено назвать геометрическим, лежит вычерчивание тех профилей, которые подлежат изготовлению. При изготовлении вычерченная форма копируется тем или иным способом, в зависимости от способа изготовления зубцов.

1) По методу копирования 3. к. изготовляются отливкой или снятием стружки. Литые 3. к.: для формовки небольших 3. к. пользуются часто формовкой по модели; при массовом производстве применяют формовочные машины (смотрите); иногда отливкой зубцам придается лишь приблизительная форма, а точная отделка производится на специальных станках. Достоинство литых 3. к.—низкая стоимость и твердость рабочих поверхностей; недостаток—

неизбежные погрешности в форме профиля-и в шаге, вследствие чего применение 3. к. с литыми зубцами ограничивается только низкими скоростями, т. к. при скоростях больше 3 м/ск колеса в работе обычно дают большой шум. Обработка снятием стружки производится в настоящее время гл. обр. при помощи дисковых фасонных фрезеров. Режущая кромка дискового фрезера имеет форму впадины зубца. Фрезер устанавливается так, что средняя плоскость его проходит через ось колеса. За один проход нарезается впадина, после чего колесо поворачивается делительным механизмом на один шаг и происходит прорезание следующей впадины. Точность работы зависит прежде всего от точности режущего профиля фрезера, а поэтому требуется особая тщательность при изготовлении и проверке последнего. При обработке твердого материала и большом модуле нарезаемого колеса рекомендуется предварительная обдирка впадины особым дисковым фрезером или же одновременное прохождение двумя рядом один за другим насаженными фрезерами, из которых один является обдирочным, а другой проходным. Развивающееся при фрезиро-вании зубцов тепло нагревает обод нарезаемого колеса неравномерно, что влечет за собой ошибку в шаге. Для устранения ошибки при изготовлении колес с точным шагом проходят впадину дважды, со снятием весьма малого слоя при втором проходе. Той же цели достигают, переходя от прорезанной впадины не к следующей, а через 3, 4, 5 и до 7 зубцов. При этом нагревание обода нарезаемого колеса происходит более равномерно, и для полного его нарезания потребуется не один его оборот, а соответственно 3, 4, 5 и до 7.

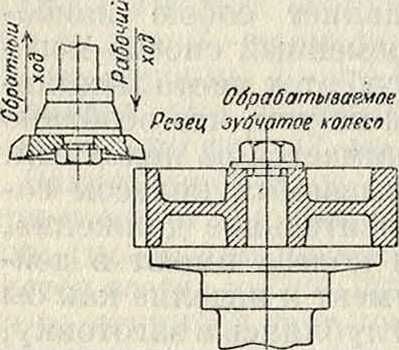
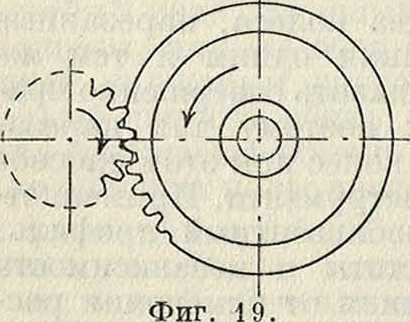
2) Изготовление 3. к. по методу обкатывания представляет собою наиболее совершенный современный способ изготовления зубцов. Способ этот чисто механический и основывается на том, что особенно простой профиль принимается за исходный. Между ним и обрабатываемым колесом создается такое же относительное движение, какое зацепляющиеся колеса имеют в действительности; инструмент и изделие как бы образуют передачу. Углубляясь в заготовку, инструмент вырезает огибающий профиль на колесе. Любые -два колеса, нарезанные по методу обкатывания одним и тем же инструментом, будут давать совершенно правильное зацепление; поэтому для нарезания набора сменных колес при этом способе достаточно одного инструмента. Применяется исключительно эвольвентный профиль, вследствие его простоты и независимости правильного зацепления от изменения расстояния между осями. Для нарезания 3. к. по методу обкатывания применяются четыре инструмента: а) зубчатая рейка, б) один зубец рейки, в) шестерня, г) червячный фрезер. а) Нарезание зубцов рейкой особенно полно и всесторонне разработано инж. Мааг, к-рый не только применил ее для нарезания сменных и исправленных эвольвентных профилей, но также изумительно разработал соответствующие зуборезные станки и авто-матич. станки для фрезирования и шлифовки самих реек, которые подвергаются после закалки шлифовке со всех сторон. Рейка представляет собою наиболее совершенный инструмент для нарезания зубцов благодаря прямолинейности ее профиля. Степень точности изготовления реек—до 0,002 миллиметров. Рейка затачивается лишь со стороны режущей кромки, благодаря чему степень точности ее остается неизменной. Для увеличения производительности, а также повышения точности изготовления зубцов применяются три рейки: для обдирки, для чистовой обработки и для обработки под шлифовку. Рейки изготовляются обычно с 8 зубцами и ок. 20 миллиметров толщиной. б) Нарезание 3. к. одним зубцом рейки представляет собою упрощение предыдущего способа в отношении исходного инструмента, который представляет призму, имеющую в сечении профиль зуба рейки. Простота и дешевизна являются главными достоинствами этого способа. Движение обкатывания воспроизводится сходно с предыдущим. Поверхность зубцов получается правильной и чистой. Станки работают долблением. При большом модуле, перед нарезанием профилей производится предварительное долбление двух пазов, в результате чего выпадает клип материала 3. к. и т. о. уменьшается количество материала, подлежащего снятью чистовым резцом. в) Нарезание 3. к. шестерней разработано и введено в жизнь в 1899 г. американцем Феллоу (Fellow), именем которого часто и называют описываемый способ. Исходным инструментом является зубчатое колесо с 24 зубцами. Резец м. б. укреплен на оправке режущими кромками вниз (фигура 19) или вверх. Последний способ предпочтителен, т. к. при нем лучше обеспечена устойчивость нарезаемого колеса, прижимаемого в этом случае сверху особым упором на супорте. Резцу и нарезаемому колесу сообщается вращательное движение обкатки соответственно тому отношению скоростей, которое имело бы место, если бы резец и колесо находились в зацеплении. г) Нарезание ци-линдрич.З.к. червячным фрезером изобретено в 1856 г., но введено в лшзнь в 1896 г. Пфаутером (Pfauter), построившим соответствующий станок. Исходным инструментом является червячный фрезер, к-рый в сечении плоскостью, перпендикулярной средней винтовой линии, дает эвольвентную рейку; рабочее движение этой рейки заменяется вращательным движением фрезера. При одноходовом червяке одному обороту фрезера соответствует перемещение рейки на один шаг; таким образом, для движения обкатки необходимо, чтобы одному обороту фрезера соответствовал поворот нарезаемого колеса на один зуб.

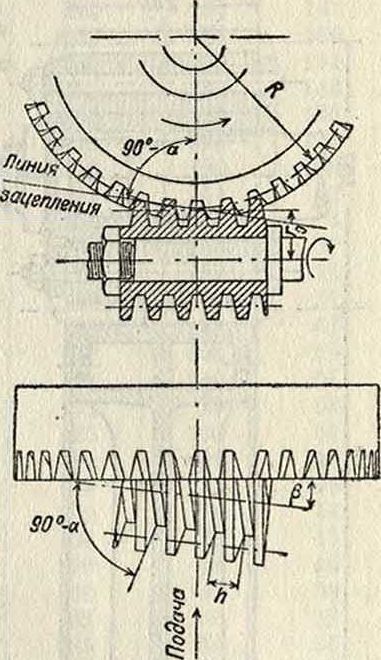
При нарезке прямого зуба фрезер устанавливается так, чтобы витки его были параллельны оси колеса, то есть ось фрезера должен быть наклонена к плоскости колеса под углом, равным углу подъема β средней винтовой линии фрезера (фигура 20). Фрезер должен врезаться в колесо настолько, чтобы начальная окружность последнего касалась начальной прямой рейки, образуемой зубьями фрезера. Кроме вращательного движения, фрезер имеет движение подачи, параллельное оси колеса. Движение обкатки таково, что в процессе нарезания находятся одновременно все зубцы, что обусловливает равномерное нагревание всего обода нарезаемого колеса и устраняет неточности, возникающие от неравномерного нагревания. Следует отметить, что режущий профиль, определяемый сечением червяка плоскостью, перпендикулярной к средней винтовой линии, не является прямолинейным,—он ограничен вогнутыми линиями, касательными к прямым теоретическ. профиля; различие между ними тем меньше, чем меньше угол β, к-рому дают обычно значение ок. 5°. Т. к. при нарезании колеса фрезер работает одновременно несколькими витками, тодлина его определяется требованием, чтобы внешние витки находились за пределами линии зацепления фрезера и колеса; в зависимости от этого фрезеру дают 5 витков для колес до 70 зубцов и 6—до 100. Заточка фрезера должна производиться в высшей степени тщательно, т. к. каждая неправильность скажется погрешностью в профиле; заточка производится на специальных станках. Значительное упрощение за последнее время внесено созданием т. н. 90°-н6го фрезера, у которого плоскость заточки проходит через ось фрезера. Для испытания червячных фрезеров применяются специальные приборы. Особенностью описываемого способа является возможность нарезания 3. к. не только с прямыми, но и со спиральными зубцами, а также и червячных колес.

Шлифование зубцов. В целях увеличения продолжительности службы колес зубцы их подвергают закалке или нитрированию. Закаленные колеса из высококачественного материала значительно дороже, но зато им можно придавать значительно меньшие размеры, чем мягким колесам. Высокая стоимость колес уравновешивается уменьшением размеров, а следовательно удешевлением всей конструкции. При закалке колеса коробятся, поэтому после нее зубцы должны обязательно подвергаться шлифованию. Шлифование зубцов производится

Фигура 20.

на специальных станках, работающих по принципу обкатывания. В станках Маага производится одновременное шлифование двух зубцов двумя тарельчатыми кругами (фигура 21). Рабочие плоскости кругов “соответствуют профилям теоретич. рейки с углом зацепления в 15°. Шлифуемое колесо совершает движение обкатывания по теоретич. рейке при помощи стальной ленты. При обкатывании шлифуемое колесо совершает качательные движения, т. к. шлифуется только одна пара профилей; одновременно с этим колесо имеет поступательное движение вдоль собственной оси. По прохождении всей длины зубца шлифуемое колесо повертывается делительным механизмом, и в шлифовку поступает следующая пара профилей. При большом модуле оба круга помещаются в одной впадине, при малом—в разных. Выносливость шлифован, закаленных зубцов может характеризоваться примером одной передачи в автомобиле, в которой после пробега в 180 000 км на поверхности зубцов сохранились следы шлифовки—крестовидные штрихи. Возможностьизготовлять прямые зубцы с весьма высокой степенью точности позволила применять их для мощных турбинных передач, В одной из установок на 3 000 ЕР применена передача с прямыми зубцами Маага при следующих данных: числа зубцов 54/119, модуль 5,2 миллиметров,

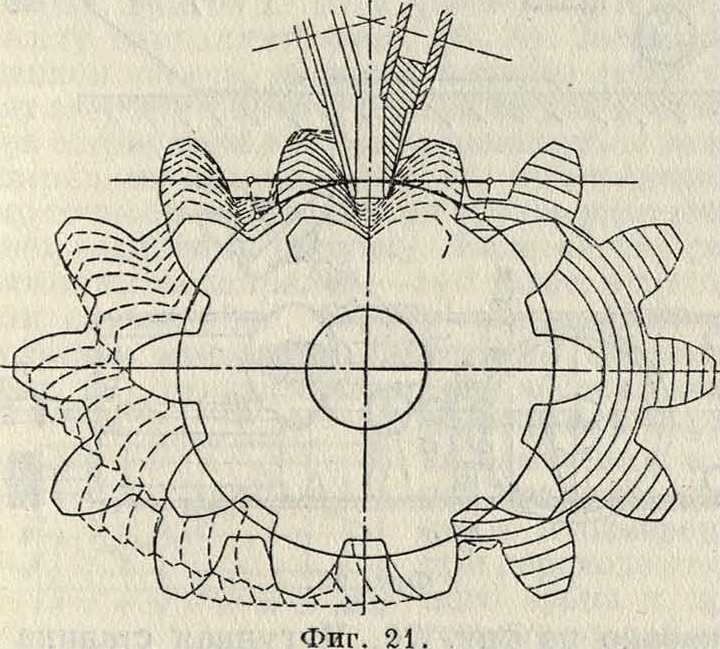
ширина колеса 355 миллиметров, число оборотов малого колеса 3 000 в мин., окружная скорость 44ж/<ж.

4. Измерения зубчатых колес. Высокие требования в отношении точности изготовления 3. к. и соответствующее развитие техники изготовления потребовали создания соответствующих измерительных инструментов и приборов для испытания колес. Типичными и вместе с тем недопустимыми погрешностями, для обнаружения и оценки которых нужны соответствующие инструменты и приборы, являются следующие: 1) эксцентричное расположение зубчатого венца на ободе—как следствие эксцентричного закрепления колеса при нарезании зубцов; 2) погрешности в шаге—как следствие неточной работы делительного механизма, неравномерного нагревания обода колеса при его нарезании и тому подобное.; 3) погрешности в профиле—как следствие неправильной формы ре жущего профиля или неправильного его положения.

Т. к. нарезание всех зубцов производится одним и тем же инструментом, то измерение эксцентриситетам, б. произведено по окружности впадин или любой концентричной ей, за исключением окружности выступов, которая обрабатывается до нарезки зубцов и может не быть концентричной с окружностью впадин.

При помощи двух калиброванных цилин-дрич. стержней м. б. определен диаметр D начальной окружности, для чего стержни вкладываются в диаметрально противоположные впадины, и измеряется расстояние между их внешними образующими. Днам. d стержней выбирают так, чтобы они касались профилей в точках начальной окружности. По фигура 22 не трудно установить, что при четном числе зубцов измеряемое расстояние М будет выражаться так:

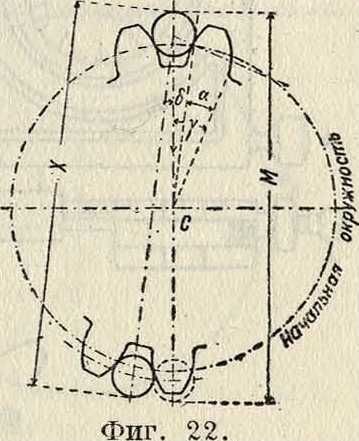
М=D [(1 + sin у) ~ - sin а],

где а—угол зацепления, у=а -δ, д ;

при нечетном числе зубцов измеряемое расстояние

X=D [(cos <5 + sin γ) - sin α].

При измерении эксцентриситета по окружности впадин пользуются индикатором, который устанавливается на неизменном расстоянии от оси вращения колеса или же поворачивается около той же оси так, что стержень индикатора может касаться окружности впадин. В том и другом случае наблюдают показания стрелки индикатора, вводя его стержень в каждую из впадин; разность наибольшего и наименьшего отклонений даст двойное значение эксцентриситета.

Измерения шага являются весьма важными, так как теоретич. исследование и опыт показали, что 3. к. весьма чувствительны к погрешностям в шаге. Измерения шага предполагают, что профиль изготовлен совершенно правильно; если этого нет, то в результатах будут сказываться погрешности совместно как в шаге, так и в профиле. Для разделения их необходимы особые испытания правильности профиля. Измеряется или шаг, как линейная величина, или соответствующий ему угол. Следует иметь в виду, что при измерении угловой величины шага на результате будет сказываться эксцентричность, что потребует затем соответствующей поправки. Измерение может производиться на любой окружности; тогда шаг будет пропорционален диаметру этой окружности, соответствующая же шагу угловая величина постоянна и от диаметра не зависит. Главную роль при измерении играет не абсолютная величина шага, а его постоянство или отклонения результатов, получаемых при отдельных измерениях. Вместо шага часто подвергают измерениям толщину зубцов или ширину впадины, в особенности для зубчатых колес, работающих в обоих направлениях.

Приборы для измерения шага весьма многочисленны и м. б. разделены по принципу

Фигура 23.

работы на следующие три группы: 1) приборы, измеряющие шаг ния эксцентриситета;

, <	ч>		Зеркало
		ч
			Зубчатое колесо
	lilii Iiiiiililii
	1 1.

с исключением влия-

2) приборы, измеряющие совместно шаг (или толщину зубца) и эксцентриситет;

3) приборы, измеряющие угловую вели-

„ чину шага. В качест-

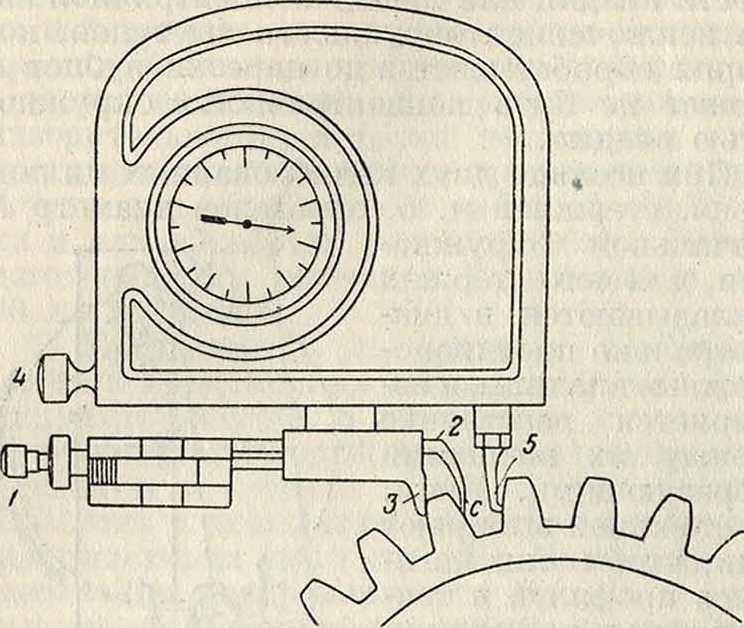
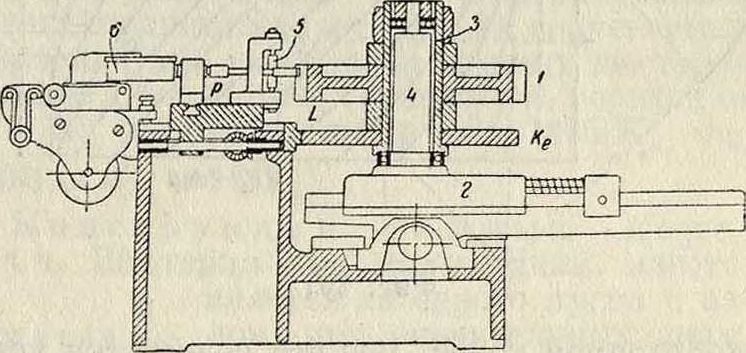
,|1 Й гхотгы»ве примера приборов первой группыIмож но указать на одонто-метр Маага (фигура 23), основанный на свойствах эвольвенты. При помощи винта 1 упор 2 устанавливается таким образом, чтобы измерительная поверхность 3 расположилась касательно к профилю. Далее, действуя винтом 4, добиваются, чтобы поверхность щупа 5 установилась параллельно поверхности 3. Перемещения щупа 5, являющиеся результатом неравенства измеряемых шагов, передаются, при помощи вращающегося на призмовой опоре рычага, стрелке индика-

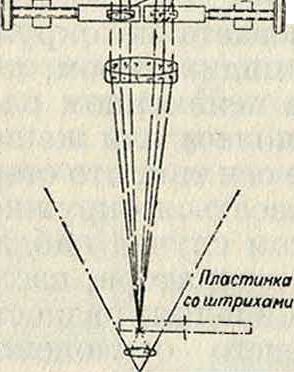
Фигура 24.

профиля. В ряде аналогичных приборов опорная точка помещается или на головке (окружность выступов) или на дне впадины.

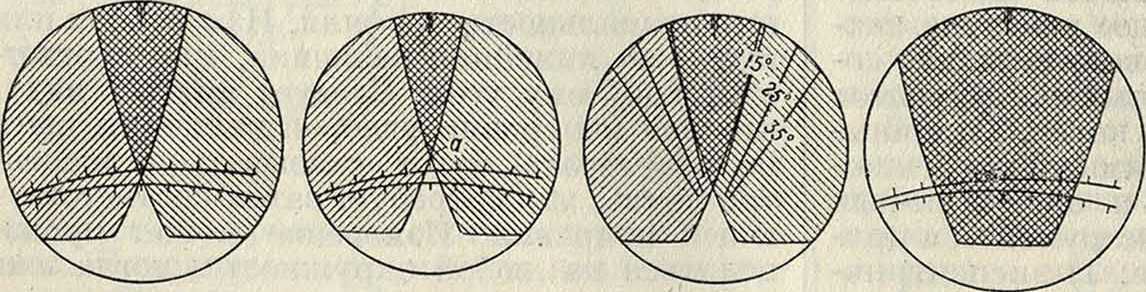
К приборам с опорной точкой на головке принадлежит общеизвестный зубомер, определяющий толщину зубца. Из приборов второй группы следует отметить оптич. прибор Цейсса, схема которого изображена на фигуре 24. Основным приспособлением является объектив, состоящий из двух раздвижных полу-линз, которые дают два изображения нижней кромки испытуемого колеса, например два изображения одного и того же зуба, располагающиеся в поле зрения микроскопа. В зависимости от относительного расположения полулинз изображения зуба перекрываются (фигура 25, А). В нулевом положении, когда обе полулинзы составляют один объектив, получается одно изображение (фигура 25, Г). Для измерения пользуются тенью, получающеюся от перекрывания одного изображения другим(фигура 25, А). Устройство прибора

Окуляр

Фигура 25А.

Фигура 25Б.

Фигура 25В.

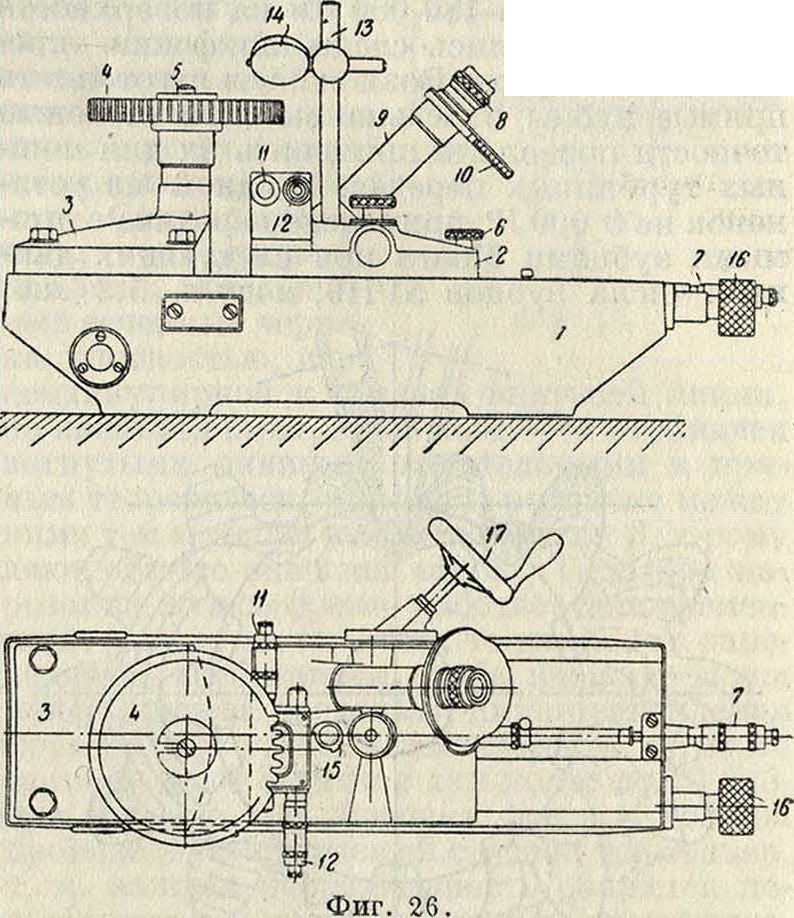
тора. Меняя щуп5, изменяют область измерения отж=2 до m=20. С описан, прибором сходен одонтометр Пратта и Уитнея (Pratt & Witney). Характерной особенностью прибора Маага является помещение опорной точки с в произвольно выбранной точке показано на фигуре 26. Чугунная станина 1 несет на себе салазки 2 микроскопа и держатель 3 для испытуемого колеса. 4, к-рое при помощи точно пригнанных букс крепится на колонке держателя и закрепляется винтом£5. Освобождая винт 6, передвигают салазки микроскопа от руки и, грубо установив их, закрепляют тем лее винтом. Точную установку производят винтом 7. Снятый со станины вместе с салазками микроскоп м. б. установлен для работы прямо на зуборезном станке при испытании больших колес, т. к. отдельный прибор допускает измерения колес диаметром лишь до 400 миллиметров. Под окуляром 8 микроскопа 9 расположена ная головка 10 со стеклянной круглой пластинкой, на которой нанесены различные штрихи для измерений. Микрометрии, винты

Фигура 25Г.

11 и 12 служат для установки полулинз. На колонке 13, которая может поворачиваться на 90°, закреплено зеркальце 14, освещающее поле зрения микроскопа. Упор 15 ограничивает угол поворота колонки. При помощи головки 16 испытуемое колесо можно устанавливать на разной высоте для получения резкого изображения зубцов. Поворот колеса производится маховичком 17 через червячную передачу.

Измерения производятся двумя основными способами: при первом — пользуются острием тени, то есть точкой пересечения налегающих друг на друга профилей (фигура 25, А и Б), при втором—боковыми очертаниями тени (фигура 25, В). При измерении погрешности шага (вернее,толщины зубца) могут быть применены оба способа. Первый является особенно удобным, когда наперед задана погрешность измерения. Для измерения служат спирали, нанесенные на стеклянном диске. Расхождение спиралей увеличивается на 0,01 миллиметров при переходе от одной пары коротких штрихов к соседней. Соответственно заданной погрешности измерения устанавливают спирали в поле зрения микроскопа так, чтобы длинный штрих соответствующего растворения спирали проходил через средний штрих (фигура 25, Б). Затем, вращая колесо, устанавливают острие тени на этом штрихе; смещая полу линзы при помощи микрометрия. винтов Ϊ1 и 12, располагают острие между спиралями (фигура 25, А). Затем, вращением колеса, на место первого зубца ставят второй, третий и т. д. Если для всех зубцов острие тени а будет располагаться между спиралями или на них,—это будет значить, что точность изготовления зубцов удовлетворяет заданному допуску. Если острие тени ляжет ниже спиралей,—зуб толст, в противном случае (фигура 25, Б)—тонок. Если результаты измерения нанести на диаграмму (фигура 27), откладывая по оси абсцисс номера зубцов в порядке измерения, а по оси ординат — разницы в измерении при переходе от одного зубца к другому, то по этой диаграмме сразу можно различить погрешности в толщине зубца от влияния эксцентриситета. На фигуре 27 большая волна кривой—следствие эксцентриситета; мелкие зубцы ее дают погрешности шага (толщины).

Устройство приборов третьей группы основано на том, что 3. к. повертывается точно на один шаг и тем или иным способом измеряется угол поворота. Приспособлением, обеспечивающим поворот именно на один шаг, является выдвижной упор, входящий во впадину между зубцами. Перед поворотом колеса упор выводится из впадины; колесо вращается и останавливается, когда упор войдет в следующую впадину. Приборы различаются между собою гл. обр. принципом действия и устройством угломерного приспособления. Точность измерений l-f-lO".

Измерения погрешностей в профиле. Устройство всех приборов основано на свойствах эвольвенты. Если

7ψ

t

о г e w и п гг ге зо зз за

Фигура 27.

окружность К_е катить без скольжения по прямой L (фигура 28), то точка О последней вычертит на плоскости катящейся окружности эвольвенту еЕ. На этом принципе построен прибор Менера (Mehner). Диск К_е (фигура 29), диам. которого равен диам. основной окружности колеса 1, катится по неподвижной прямой линейке L, к которой прижимается пружиной вместе с салазками 2. Колесо и диск

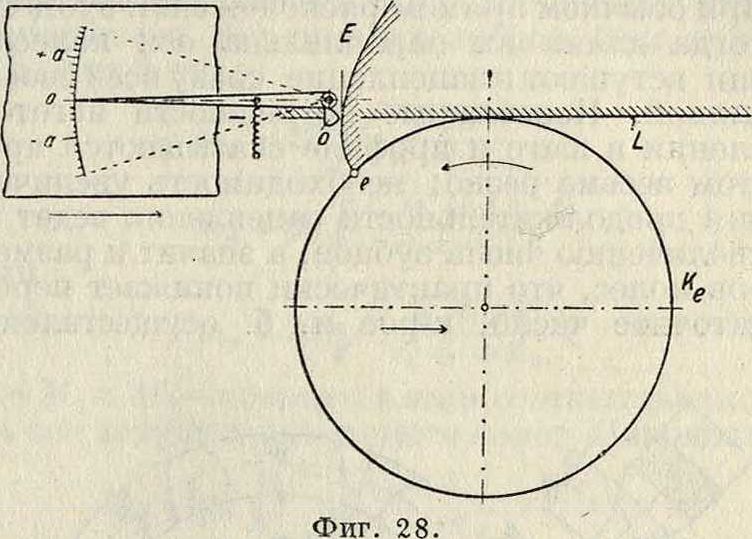
закреплены на буксе 3, насаженной на цапфу 4, установленную на салазках 2. Угловой рычаг 5 закаленной и шлифованной острой кромкой О, (или 0{) короткого плеча прижимается к испытуемому профилю в точке О (фигура 28), а длинным плечом касается стержня индикатора 6. Если профиль правилен, то стрелка индикатора не отклоняется от

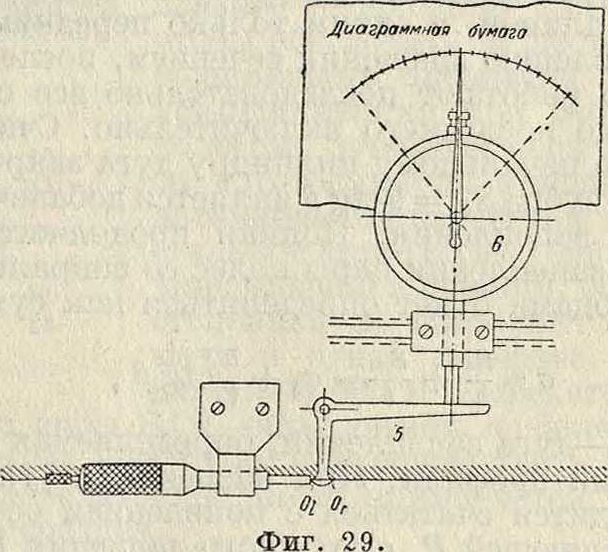
нулевого положения при скольжении кромки О, по профилю зуба во время качения диска К_е по линейке L. При неправильном профиле происходит отклонение стрелки в ту или другую сторону. Устройство прибора не только допускает отсчет погрешностей, но и записывает диаграмму их. Недостатком прибора является необходимость иметь набор дисков К_е для колес разных диаметров.

Помимо приборов для измерения отдельных погрешностей, в практику вошел ряд таких, которые имеют целью общее испытание построенных 3. к. Приборы эти чаще всего позволяют дать лишь качественную оценку работы 3. к., реже—количественную.

5. 3. к. со спиральными и угловыми зубцами. При обычном прямом расположении зубцов, когда длина их параллельна оси колеса, они вступают в зацепление сразу всей своей длиной. Неизбежные погрешности изготовления в шаге и профиле сказываются при этом весьма резко; необходимость увеличения продолжительности зацепления ведет к увеличению числа зубцов, а значит и размеров колес, что практически понижает передаточное число, к-рое м. б. осуществлено

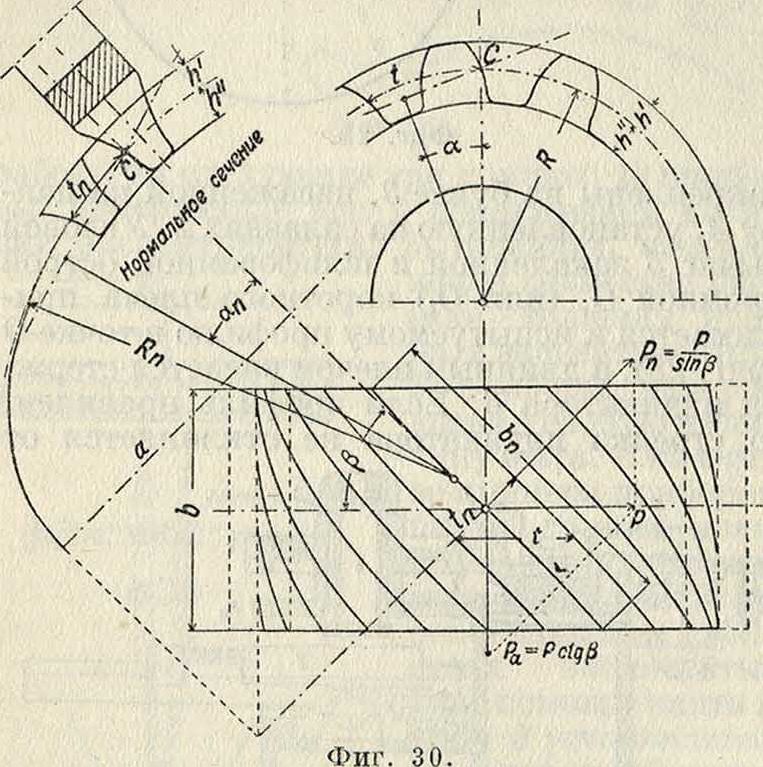
одной нарой колес. Все эти недостатки устраняются применением спиральных зубцов, которые представляют собою винтовую нарезку с постоянным ходом (фигура 30). При зацеплении зубец вступает в работу не сразу всей своей длиной, а одним только передним но направлению вращения сечением, после которого работают последовательно все сечения, до последнего включительно. Считаемая по начальному цилиндру дуга закручивания зубцаS_d.=bctg β является добавочной дугой зацепления. Полная продолжительность зацепления пары колес со спиральными зубцами будет определяться как сумма:

^{σ =} Т + Т"=^σο + j ctg β,

где So—дуга зацепления, определяемая элементами профиля. При назначении угла β приходится считаться с появлением осевой составляющей Р_а окружного давления Р на зубец, которая вызывает добавочное трение в опорах. Р„=Р ctgнормальное давление р на зубец Р„==—. В простых колесах со спиральными зубцами β назначается в пределах от 80 до 60°. Для устранения осевого давления применяются угловые зубцы,к-рые к тому же оказываются значительно прочнее прямых, если только в зацепление они всту--пают углом. Для колес, работающих в обоих направлениях, зубцам дается двойной излом,

При расчете и изготовлении колес со спиральными или угловыми зубцами следует иметь в виду форму и размеры зубцов и величину шага в нормальном сечении (фигура 30). Сечение начального цилиндра нормальной плоскостью даст эллипс с большой полуосью а= _sin ^ и малой полуосью Ь=В. Радиус В_п

круга кривизны в точке С, равный,

можно рассматривать приближенно как радиус начальной окружности нормального сечения. Нормальный шаг t_n зависит от окружного шага ί след, образом: l„=fsin/5, откуда число зубцов на полной окружности приближенного нормального сечения

2л R_n, z

^Zn ~ t„. ~ ЙНч»

Полученные соотношения позволяют перейти от колеса со спиральными зубцами, характеризуемого величинами z, t и β, к колесу с прямыми зубцами и соответственными величинами ζ_η и t„. Т. о., нарезание спиральных или угловых зубцов моя«ет производиться теми же инструментами, которые употребляются для прямых, до только инструмент следует подбирать по величине нормальн. модуля т_п=~. Высота головки зубца будет h=m_n и ножки h"=_вт„. Между углами зацепления а и а_п существует соотношение: tga=~^jj· Если спиральные зубцы будут нарезаться обычными инструментами для прямых зубцов с углом а= 15°, то а_п== 15°, откуда а=17°1130" при /5=60° и а=20°4513" при /5=45°. Соответственно этому минимальное число зубцов z=20 при β=60° и z=12 при /5=45°. При дальнейшем уменьшении числа зубцов будет происходить подрезание их, во избежание которого потребуется вводить исправление профилей; при этом условии число зубцов может быть доведено до трех.

Расчет спиральных зубцов ведется по ф-лам и данным для прямых зубцов, причем определяется расчетом нормальный модуль т_п= · Для колес с литыми и необработанными угловыми зубцами b=3-p4t, β== 55 -р 65°; высота головки h=0,251,высота ножки h”=0,35ί, толщина зубца по начальной окружности равна 0,46ί. Угол а зацепления в плоскости колеса равен 18°, для малого числа зубцов он увеличивается до 25°. Материал—чугунное или стальное литье. Благодаря высокой прочности зубцов 3. к. с угловыми зубцами применяются для тяжелых передач с ударной нагрузкой (в прокатных станках и тому подобное.). Для угловых обработанных зубцов обычно Ь=3<; при возрастании окружной скорости и передаваемой мощности Ь повышается до 5 ί. Обычно /5=60-р 45°, нек-рые заводы доводят β до 18°. Возрастающая с убыванием β продолжительность зацепления позволяет уменьшить число зубцов на малом колесе до 16, при средних значениях окружной скорости и отливке малого колеса из чугуна или стали.

При изготовлении шестерни из кованой стали число зубцов уменьшается даже до трех. Соответственно такому уменьшению числа зубцов передаточноечи-ело м. б. осуществлено I до 30 в одной переда-

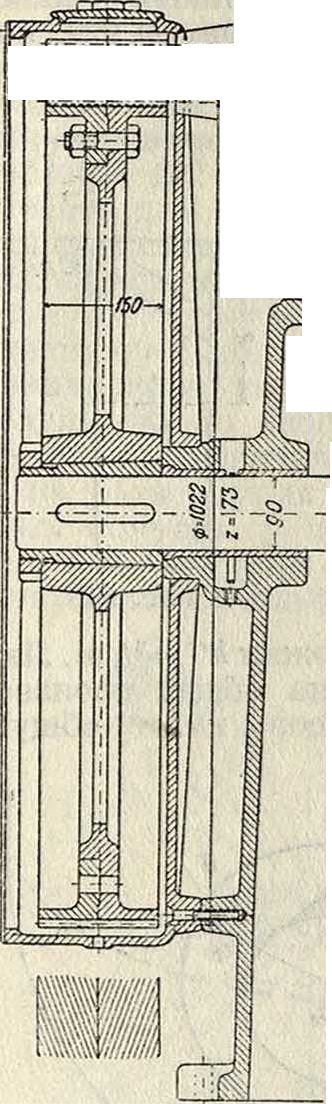
^ че. Кпд=0,95. Констру кция колес с угловыми зубцами представлена на фигуре 31.

3. к. с угловыми или спиральными зубцами, Ш работающие при больших окружных скоростях и передающие большие мощности, получили особое название — передач высокой мощности (Hochlei-stungsgetriebe). Окружная скорость в передачах от паровых турбин достигает 70 м/ек, и нет оснований считать эту скорость предельной.

Требования к материалу колес сводятсяк следующим: 1) материал должен хорошо обрабатываться и давать при этом чистую поверхность; 2) он должен обладать практически неограниченной сопротивляемостью изнашиванию и 3) материалы колеса и шестерни должны хорошо работать совместно. Таблица 3 дает указания о применяемых для мощных передач материалах и их механические характеристики но данным завода Brown, Boveri & Со. A.-G.

Т а б л. 3.—М е х а и и ч е с к а л характеристика материалов, применяемых для мощных передач.

Фигура 31.

Расчет мощных передач. При расчете мощных передач исходят из других оснований по сравнению с расчетом обычных передач с прямыми зубцами. Ширина b шестерни берется в зависимости от ее диам. D^. b=xD₁; сс=1,2-рЗ,2. Обозначая нормальные шаг и модуль через t_n и т_п и принимая во внимание вышеуегановленные соотношения между z, t, β и z_n, t_n, можно воспользоваться для расчета т уравнениями, установленными для прямых зубцов. Они примут такой вид:

sin β~

~к,7.

«.-VsSS

- 99

п ~~ у ζΐ.χ.κ,.’ т_н=22 у/~

т.

Мо sin² β ζ_χ· ζ₂-χ·Κ".

где М_г и М₂—моменты в тем соответственно на оси ведущего и ведомого колес. Наконец:

то,=912

V-

ή ⁼ 912 j/^ —

N sin² β z}. τι, · χ· К,i

N sin² β

ζ₂· n₂ χ· Кц.

Изгото вляемые части	Материал	Врем, сопротивление на разрыв в килограммах/мм2	Предел текучести в килограммах/мм2	Относит, удлинение в % при Ю-кратнон длине обр.
Шестерни	Низкопроцентная никелевая или хромоникелевая сталь.	65—75	40	18
»	Специальная сталь.	80—85	45—50	12
Обода колес	Симеис-мартеновская сталь ..	52—60	30	18
»	Специальная сталь.	65—75	35—40	14

Наименьшее число зубцов z=25, зубцы— эвольвентные. Выс. головки h=0,S~l,0 т, высота ножки h"=1,04-1,2 то, высота зубца А=1,8-т-2,2то. Шаг и модуль должен быть по возможности малыми. Обыкновенно m=2r~8. Меньшие значения берутся для больших скоростей и малых колес. Угол /3=80-1-45°. Смазка зубцов имеет огромное значение; при скоростях выше 12 м/ск масло подается под давлением и вбрызгивается между зубцами. Коэффициент полезного действия ц, включая потери в подшипниках, равен 9,97-1-0,99.

Вместо допускаемого напряжения К_и. задают обыкновенно величину допускаемого давления р в «г на 1 сантиметров ширины шестерни. Значе-чения р в функции от диаметра шестерни, но данным Brown, Boveri & Со. представлены диаграммой (фигура 32). Заштрихованная площадь представляет область допускаемых значений для р, полагая ширину шестерни равной 1 см. Можно осуществить переход от р к К_и, но уравнению р=0,01885 К_и.-т_п,

откуда К,.=53,1 ~.

^тп

Конструкция мощных пере-дач. Шестерня при малых диам. изготовляется из одного куска с валом; при значительных диам. она изготовляется отдельно и насаживается навал так,чтобы она имела возможность некоторого осевого движения. Последнее необходимо для того, чтобы обеспечить за шестерней возможность автоматич. само-устанавливания при работе с колесом. Зубчатый ооод колеса изготовляется отдельно и насаживается на чугунное или стальное литое колесо (фигура 33). Наибольшая мощность, осуществленная до настоящего времени в одной передаче, равняется 15 000 1Р. Передаточное число пары 3. к. обыкновенно не более 25. В случае необходимости осуществить большее передаточное число применяется двойная передача.

Изготовление 3. к. со спираль-н ы ы и и у г л о в ы м и зубцам и производится теми же методами, как и обычных колес. По методу копирования спиральные и угловые зубцы могут быть изготовлены модульным дисковым фрезером, средняя плоскость которого должен быть установлена под углом 90-/3° к оси колеса (фигура 34 а); последнее должно в этом случае получить добавочное вращение с окружной скоростью υ, связанной со скоростью с подачи зависимостью:

= tg β. При обработке угловых зубцов этим способом требуется оставить между зубцами правого и левого хода достаточный промежуток. Хорошие результаты дает применение концевого профильного пальцевого фрезера, который является особенно удобным ДЛЯ изготовления угловых зубцов (фигура 346). Недостаток указан, фрезера — затруднительность заточки.

По методу обкатывания спиральные зубцы м. б. изготовлены всеми четырьмя юо 200 зоо ^ •уда»»· инструментами, ука-^а занными выше. При

Фиг Я 9 ¹

^{Ч И1}· ^οί· нарезании спираль ных зубцов по способу Феллоу .резец должен иметь тоже спиральные зубцы. Сайкс (Sykes), применяя резцы Феллоу, сконструировал для нарезания угловых зубцов особый станок, на котором совершенно точно выбирается материал в углах зубцов. Червячным фрезером нарезаются как спиральные зубцы, так и угловые. При этом могут представиться два случая: 1) направления спиралей колеса и витков фрезера одинаковы (оба левые или оба правые); 2) направления спиралей колеса и витков фрезера различны. В первом случае ось фрезера ставится под

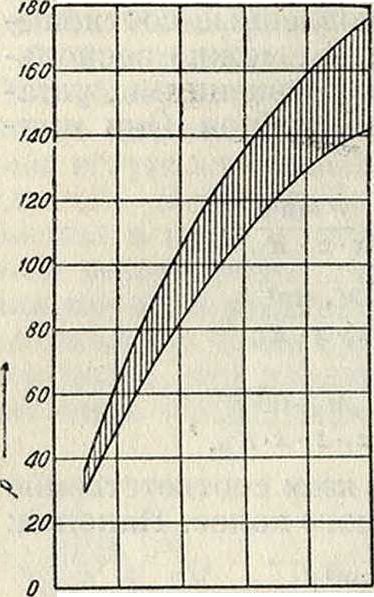
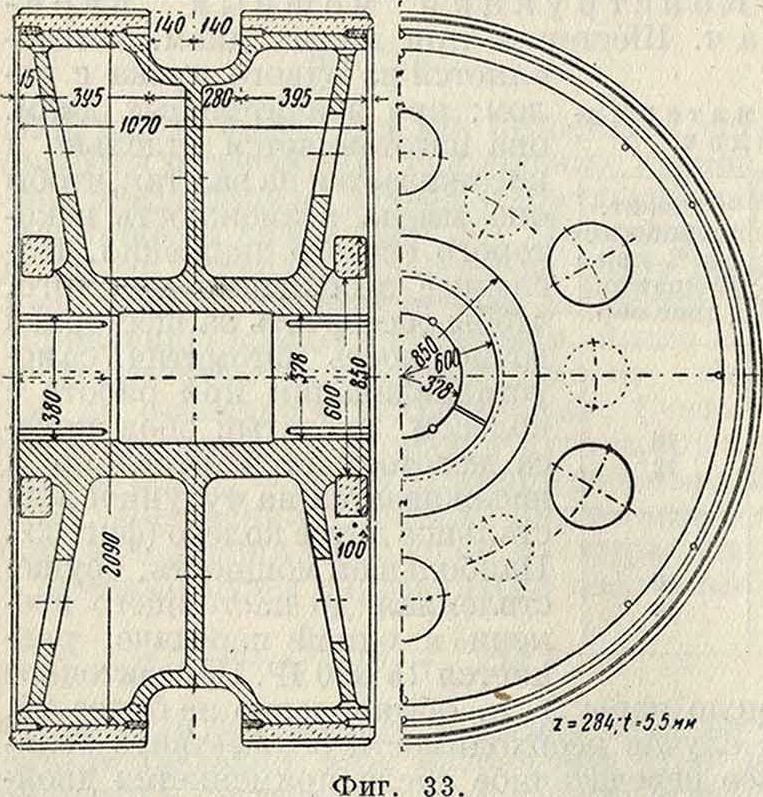
углом β—β₃ к оси колеса, во втором—под углом β + /?, где β—угол подъема спирали на колесе и jS_s—угол подъема витков фрезера.

II. Конические колеса.

Конич. колеса служат для передачи вращения и работы между пересекающимися осями. Конусы I и II (фигура 35), перекаты вающиеся один по другому без скольжения, являются аксоидами, определяющими относительное движение двух тел, вращающихся около осей ОО_г и 00₂ с постоянным отношением угловых скоростей к. Конусы эти, называемые начальными или делительными, снабжаются зубцами, размеры которых выражаются также, как и для цилинд-рич. колес. Обычно высота

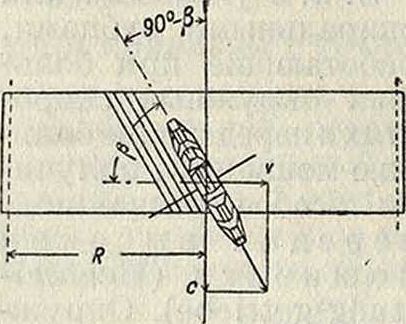
Фигура 34а.

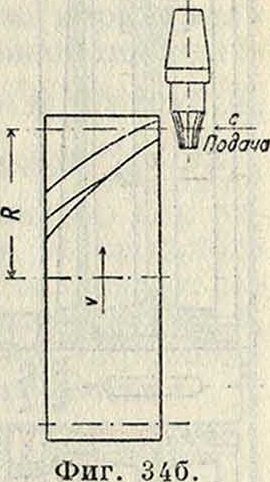
головки=высота поиски 1ι"=⁷Ι_βνι. Любая точка С, лежащая на общей производящей начальных конусов, имеет общую

I

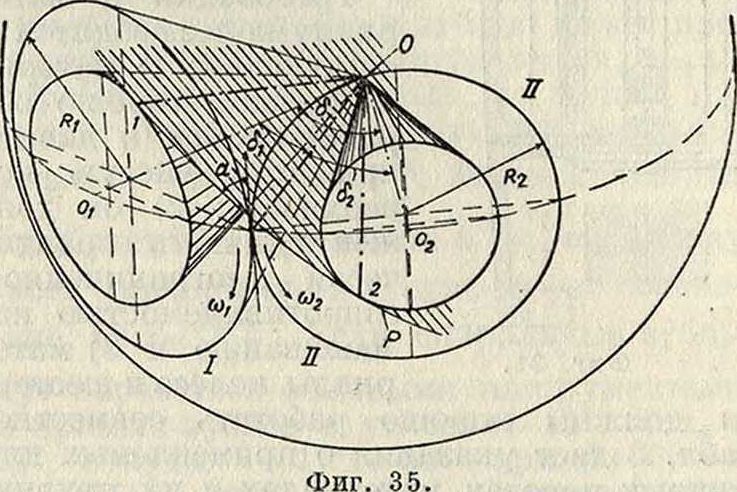
для обоих конусов скорость ν=β₁ω₁= R₂co₂; отсюда—передаточное число

О)j Ii2 Z2 Sin δ₂ω₃ Ri~ z_x~ sin ’

где и б ₂—углы общей производящей с осями ОО_ги 00₂, δ=δ_χ- -δ₂—угол между осями, R_x и R₂—радиусы начальных окружностей, считаемые по наибольшим сечениям конусов, z_x и ζ_%—числа зубцов. Углы и <S₂ определяются соотношениями:

ctg <

ft + cos в и ctsr <5„ =

, + COS δ

Обыкновенно угол <5=90°, тогда ctg д_х=к=

Ή

и ctg <5₂=“ · Поверхность сферы с цен тром в точке О, радиуса ОС или иного произвольно взятого, пересечет поверхность конусов по окружностям 1-1 и 17-Л, которые при качении начальных конусов будут катиться без скольжения одна по другой на поверхности сферы подобно тому, как начальные окружности цилиндрич. колес катятся друг по другу в плоскости, перпендикулярной осям колес. Цилиндрич. колеса представляют собою частный случай конических с углом ό=0°.

Можно показать, что простейшими профилями для зубцов конич. колес будут: 1) сфе-рич. циклич. кривые и 2) сферич’. эвольвенты круга [¹²]. В машиностроении применяются почти исключительно эвольвентные профили, как более простые для изготовления и установки. Плоскость Р, проходящая через общую производящую ОС и касательная к двум основным конусам 2 и 2, лежащим внутри начальных, является поверхностью зацепления. При навивании плоскости Р на основные конусы 2 и 2 производящая прямая ОС даст профильные поверхности зубцов для конусов I и II. Угол а между плоскостью Р зацепления и плоскостью, касающейся по прямой ОС обоих начальных конусов, будет углом зацепления. Как и для цилиндрич. колес, а= 15° или α=20°. Профилирование выполняется весьма часто приближенно по способу Тредгольда, предложившего вычерчивать профили не на сфере, а на развернутых плоскостях дополнительных конусов, у которых 1) производящие перпендикулярны к производящим соответствующих начальных конусов; 2) вершины ху лежат в точках

А 2 на осях начальных конусов; 3) основаниями служат основания начальных конусов (фиг .36). Такая замена возможна благодаря тому, что для вычерчивания профилей нужна узкая полоска сферич. поверхности, ширина которой равна высоте зубца, представляющей, сравнительно с радиусом О С,малую величину. Поверхности дополнительных конусов развертываются на плоскость, и на двух начальных окружностях Г и 11, проведенных из центров А_ги А 2 радиусами .Α₁0=ρ₁ и А₂С=д₂, вычерчиваются профили по правилам, изложенным для цилиндрических колес.

Вопрос об очертании профилей конич. колес с чи зубцов и z₂ сводится к очертанию профилей соответственных цилиндрических колес I-l и II-II с чи зубцов г_г и z₂. Зависимость между z_u г_ и z{, z₂дается уравнениями

, _ Bzf + zi + SzjZ.cos и z, — z,

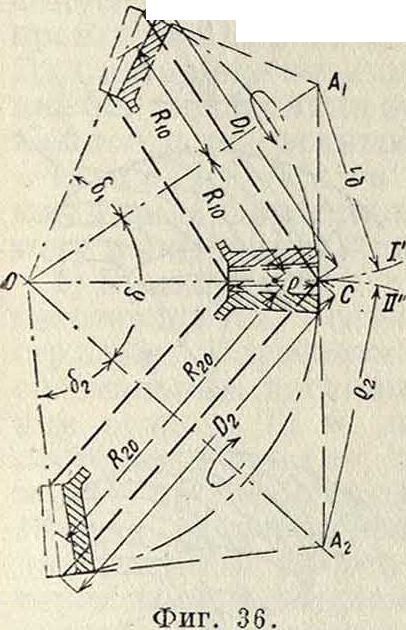
и

К=z.

z₂ + z,cos <5

Ϊ + zi + 2z,ZjCOS 6

z, +Z₂COS д если принять во внимание, что

R,. _ R

01 =

cos <5, ^:

02 =

cosij

V

sin d_. р _

k 4- COS (5 ’ ^{1 —}

й₂=<5 ;

_Λ mz, _Т mzo mz.

01= _T‘; ^Jt* ₂ ; е“=т

В частном случае, при <5=90°,

„ Vzi+zi — ^ζι ; у

z*=2«

Y z + z

и

Навертывая окружности Г-1 и ΙΓ-ΙΓ с вычерченными на них зубцами на поверхно сти соответствующих дополнительных конусов и проводя прямые к вершине О через каждую точку профилей, получим профильные поверхности зубцов конич. 3. к. в виде

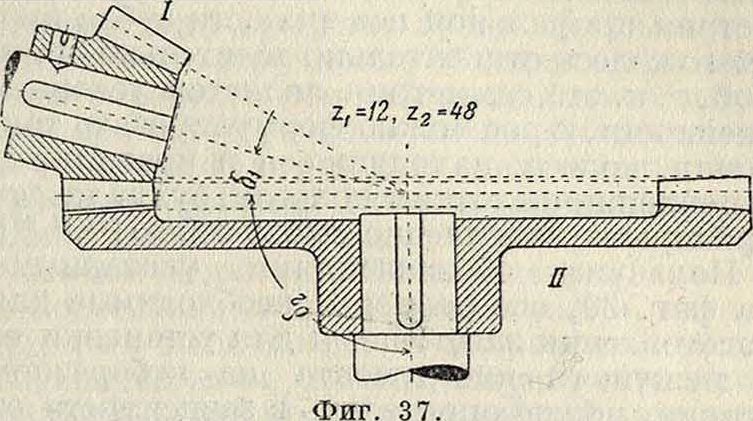
конич. поверхностей с вершинами в точке О. Погрешность от замены истинного профиля приближенным невелика; с увеличением числа зубцов, при данном модуле и угле конуса, она уменьшается. При 9 зубцах и угле конуса в 45° она составляет 1 % от модуля, при 35 зубцах—0,1%[²⁶].

В частном случае, когда один из обоих углов, наир. δ₂, равен 90°, начальный конус колеса II обращается в плоскость (фигура 37). Плоское колесо II аналогично рейке ци-линдрич. колес; дополнительный конус для

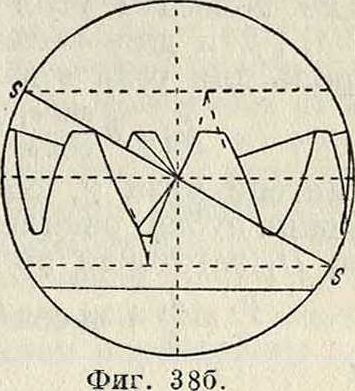
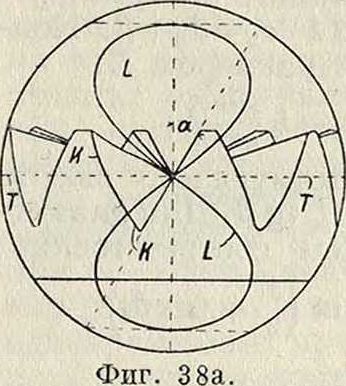
него обращается в цилиндр. Приближенное очертание дает в развернутом виде прямолинейные профили рейки. Соответственно этому, профильные поверхности плоского колеса будут плоскостями, которые в пересечении с поверхностью шара дадут дуги КК большого круга(фигура

38а) и будут наклонены к начальной плоскости ТТ под углом 90° — а, где а—угол зацепления.

Если на поверхности шара построить для профиля КК линию зацепления, то вместо дуги SS большого круга (фигура

386), как должен быть для точного профиля по сферич. эвольвенте, получим сферич. лемнискату LL, по форме которой это приближенное зацепление получило название октоидального. Октоидальноеплоское .колесо имеет весьма важное значение для

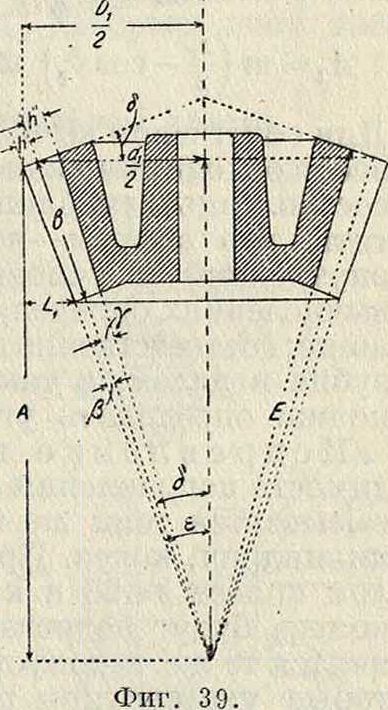
22

Т. Э. m. VIII.

изготовления конич. колес, т. к. допускает при изготовлении конич. зубцов по методу обкатывания применение инструмента с прямолинейной режущей кромкой. Существенным обстоятельством является при этом симметрия профильной поверхности зубца плоского колеса относительно делительной прямой, т. к. эта симметрия является условием сменности, к-рое можно формулировать так: конич. колеса, находящиеся в правильном зацеплении с плоским колесом, будут давать правильное зацепление между собою С¹¹,¹⁴,²⁶].

Пользуясь обозначениями, указанными на фигуре 39, все размеры, необходимые для изготовления заготовки и для установки ее и режущего инструмента на зуборезном станке, можно определить в зависимости от основных данных—т, z_lt z₂, Ь—следующим образом. При угле между осями <5=90° имеем:

ctg=ic=-~^г и ctg δ₂ =*= *!.

Λ·1 Γί ~2

Называя через β угол, соответствующий головке зубца, имеем:

tgj?=-

h

<й

/?

а т. к. h=т, d₁=m^₁ и d₂=w,г₂, то

Для колеса I угол внешнего конуса εχ==<5!+/? и для колеса II ε₂=δ₂ + β. Контроль для угла ε дается размером L:

Sin е,

и L,=b -

^ ^ cos D “ "² ” cos β

Тангенс угла γ, соответствующего высоте ножки зубца, равняется ⁷/„ tg β. Для диаметра D₁ заготовки получаем соответственно:

Щ-=Y + Ш cos <5χ=m + cos ^

И

^т (г“ + cos <5₂) ·

Для установки заготовки на зуборезном станке важны размеры А и Е, для которых имеем:

Е=т у —_t^A-i=^m (д - ^{cos й}а) И=^т (f ~ ^cos ^ι) ·

а)²

Для облегчения вычислений, определяющих все необходимые размеры, пользуются особо составленными таблицами [¹⁹]. Следует отметить, что конусы—начальный, наружный, внутренний и основной—удобно во всех вычислениях определять их углами при вершине ; соответственно этому удобнее и высоту зубца в целом, а также высоты головки и ножки определять угловыми величинами.

Исправление профилей. Необходимость исправления профилей конич. 3. к. вызывается теми же причинами, что и для цилиндрич. колес. При числе зубцов на малом колесе 2=525 и 1,5 :1 зубцы малого колеса будут подрезаться, следствием чего явятся те же недопустимые явления, на которые указано при рассмотрении цилиндрических колес. Исправление сводится к увеличению эвольвептной части зубцов малого колеса и осуществляется теми же приемами, что в цилиндрич. колесах (смотрите выше).

При нарезании зубцов по методу обкатывания инструментом с прямолинейной режущей кромкой, представляющей собою профиль зубца соответственного плоского колеса, универсальным методом исправления является, как и для цилиндрич. колес, метод смещения инструмента. Исправление конич. зубцов характеризуется, однако, не линейным, а специально угловым смещением инструмента [^п].

Для лучшего распределения давления между зубцами, увеличения продолжительности зацепления и более плавной работы конич. колес, вместо прямых зубцов (фигура40, А) применяются косые или тангенциальные

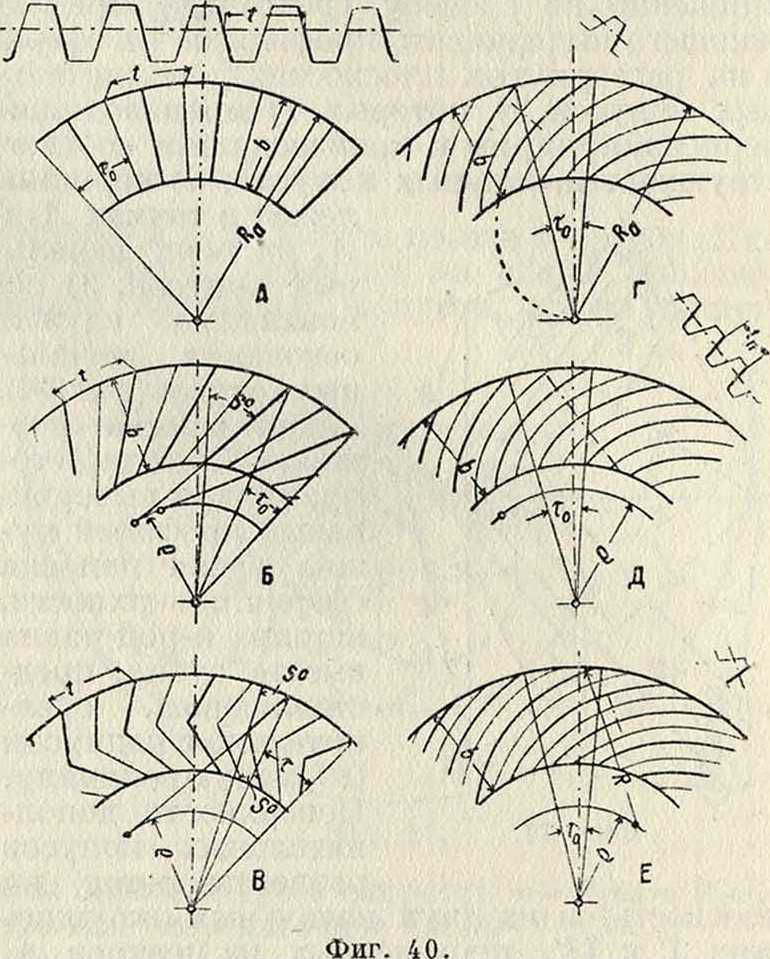
(фигура 40, Б), угловые (фигура 40, В), спиральные (фигура 40, Г), эвольвентные (фигура 40, Д) и круговые зубцы (фигура 40, Е). Все перечисленные изображения относятся к плоским колесам. Замена прямых зубцов косыми, угловыми и т. д. позволяет также повысить передаточное число пары колес до 10, тогда как при прямых зубцах передаточные числа выше 4 применяют неохотно.

Сведёние вопроса об очертании профилей конич. колес к вопросу об очертании соответственных цилиндрич. 3. к. позволяет перенести все зависимости и результаты опытов над цилиндрич. колесами на конические 3. к.

Расчет зубцов конич. колес ничем не отличается от расчета цилиндрич. 3. к. и выполняется по тем яге ф-лам. Расчетом определяется модуль или шаг для средних радиусов Д₁₀ и 11₂₀ (фигура 36); длина Ь зубца, измеряемая общей образующей, определяется в зависимости от окружной скорости, путем соответственного назначения величины ψ=b/т, которая берется в пределах от 6 до 15, причем большим окружным скоростям соответствуют ббльшие значения у. Определив расчетом величину т₀ для средней окружности, переходят от нее к окружности большого основания и модулю т, ей со-

ответствующему. R_l0=R_t —·sin д_г; так как г» TflZt ί~ 1ΎΙ₀Ζι, b. с

1<Ч- -₂ И R₁₀= y, TO m=m₀ + -sin <5j.

Вычерчивание и обмер зубцов производится по большой окружности. Толщина обода берется в пределах от 0,451 до 0,61, у чугунного 3. к., сцепляющегося с колесом с деревянными зубцами,—от 0,41 до 0,5ί. Толщина обода со вставными деревянными зубцами делается равной 1. Число спиц, их размеры, а также и размеры втулки можно определять теми же приемами, какие были указаны для цилиндрич. 3. к.

Особенностью конич. 3. к. являются возникающие при работе зубцов усилия Sj вдоль осей колес. Величина осевого усилия S₁ определяется по окружи, усилию Р: Si=Р tg а sin ε_χ и S₂=P tg а cos, где а—угол зацепления, равный обычно 15 или 20°, 2βχ—угол при вершине внешнего конуса и Sг—составляющая давления, направленная перпендикулярно к оси колеса. Для воспринятая и передачи осевых давлений на подшипники валы конич. 3. к. снабжаются установочными кольцами [²,⁹,¹³, ¹⁴].

Изготовление конических З.к., как и цилиндрических, производится по методу копирования или обкатывания.

1) По методу копирования зубцы изготовляются отливкой [^в] или снятием стружки. Нарезание зубцов производится специальным дисковым фасонным фрезером или резцом. Т. к. дисковый фрезер имеет постоянное сечение, то нарезание им зубцов может производиться лишь приближенно. Подача фрезера происходит параллельно дну впадины. Работа производится на универсальном фрезерном станке. Достоинство способа — невысокая стоимость работ вследствие отсутствия затрат на специальный станок. Фрезер требует специального изготовления. Форму режущей кромки можно подобрать так, что профиль зубца получится с той же степенью точности, как и при нарезке цилиндрических колес модульными фрезерами [²⁷]. Вместо дискового фрезера иногда применяется фасонный концевой (пальцевый) фрезер. Колеса, нарезанные дисковым или концевым фрезером, могут применяться только при небольших скоростях. Получение точного профиля зубца при обработке его резцом достигается применением шаблонов, профили которых очерчиваются или точно по сферич. эвольвентам или приближенно по плоским. Шаблоны изготовляются в виде пластин или тел вращения и устанавливаются на станине зуборезного станка так, что прямолинейная режущая кромка резца описывает при рабочем ходе последнего плоскость, проходящую через вершину конуса колеса и касательную к профилю шаблона в соответствующей точке. Станки, вырабатывающие конич. зубцы по шаблонам, делятся на две группы. В первой—обрабатываемое колесо неподвижно, и все необходимые для получения профиля движения выполняет резец, направляемый шаблоном. В станках второй группы резец совершает только прямолинейно-возвратное рабочее движение, а движения, необходимые для получения криволинейного профиля,

совершает обрабатываемое колесо. Т. к. профиль конического 3. к. зависит от числа зубцов и угла при вершине основного конуса, то для каждого колеса требуется особый шаблон, если поставить требование точного соответствия профиля зубца профилю шаблона. Это затруднение обходится применением определенного набора шаблонов, которые для соответствующего числа зубцов дадут точные профили, а для всех остальных— приблизительные. Колеса, нарезанные на таких станках, не годятся для работы при высоких скоростях. То же следует сказать относительно станков одонтографич. типа, в которых шаблона нет, а направление резца осуществляется особым шарнирным механизмом, дающим криволинейный профиль, близкий к эвольвентному, в результате сложения двух движений [*].

2) Нарезание зубцов конич. колес по методу обкатывания является наиболее совершенным способом их изготовления. Исходный инструмент имеет прямолинейную режущую кромку, то есть является профилем октоидального. плоского колеса, по к-рому и совершается движение обкатывания обрабатываемого колеса. В станках, работающих по методу обкатывания, должны выполняться следующие двюкения: а) движение обкатывания между нарезаемым колесом и инструментом, б) рабочее движение инструмента, в) делительное движение, то есть подача на зуб. Помимо этих движений в нек-рых станках добавляются: г) во фрезерных станках—подача фрезера вдоль зуба, д) отвод резца или нарезаемого колеса при холостом ходе инструмента. Движение обкатывания выполняется или обрабатываемым колесом, причем инструмент совершает только рабочие движения, или, в большинстве станков, одновременным вращением нарезаемого колеса и инструмента.

Для измерения элементов зацепления (профиля, шага, эксцентричности) коническ. 3. к. могут быть применены многие из инструментов, употребляемых для измерения цилиндрических 3. к. Для испытания конических 3. к. чаще применяются машины типа Штифельмайера, которые дают диаграммы работы колес.

III. Гиперболоидальные колеса.

Гиперболоидальные колеса служат для передачи работы и вращения между перекрещивающимися осями. Акеоидами, определяющими относительные движения двух тел, вращающихся около перекрещивающихся осей I-Ι и II-II (фигура

41) с постоянным отношением угловых скоростей “=к, являются два гиперболоида вращения. Поверхности их, служащие начальными поверхностями гипер-болоидальных колес, касаются одна другой

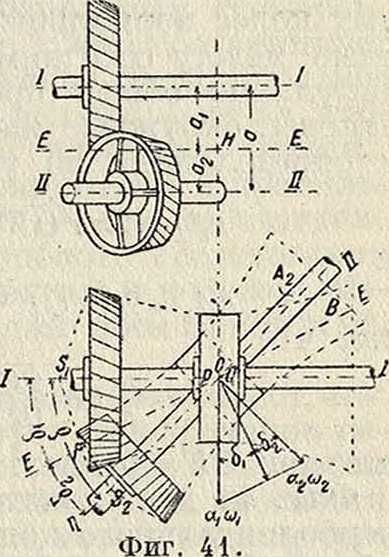
по производящей ЕЕ, которая делит: 1) кратчайшее расстояние а между осями 1-1 и 11-11 на отрезки α₁+α₂=«·; 2) угол и между проекциями тех же осей на плоскость, перпендикулярную линии кратчайшего расстояния, на части Sj-f-<5₂= <5. Как и в конических колесах,

^ _ со, _ z₂ _ sin δ₂«>2 z_x sin όχ ⁵

T. e.

, ο k -j- COS δ. 4 h

ctg δ_±=- _{aIn т} и ctg δ₂ =

+ cos δ sin ό

Чаще всего <5=90°. Гиперболоиды вращаются около своих осей с угловыми скоростями <»! и ω₂ и скользят вдоль общей образующей ЕЕ со скоростью c=aco₁-sia5₁. Окружная скорость гиперболоида 1 на линии кратчайшего расстояния равна «!<»!, а гиперболо-из треугольника же скоро-

ида II—a₂a>₂; стей получим:

а, _ tg в, а, ^— tg д₂

а также то есть %= а

1?

tg (5, + tg б₂ ’

ft, COS i, a., cos л.

Для изготовления 3. к. используются только части поверхностей гиперболоидов, как указано на фигуре 41; зубцы прямолинейные и направлены по образующим гиперболоидов. Вследствие сложности точного профилирования применяется приближенное очертание профилей, которые строятся, как и для конич. колес, на поверхности дополнительных конусов с вершинами в точках Si и S₂. Погрешность такого построения тем больше, чем ближе к жерло-вому сечению лежит сечение, для которого строятся зубцы; а так как в жерловом сечении и скорость скольжения, сравнительно с окружными скоростями, имеет наибольшее значение, то жерловой частью по возможности избегают пользоваться для устройства этих колес. Для гиперболоидаль-пых колес нормальные шаги отсчитываемые между соседними профилями перпендикулярно общей производящей ЕЕ, одинаковы, окружные же ί_χ и <₂ неодинаковы и определяются из уравнений

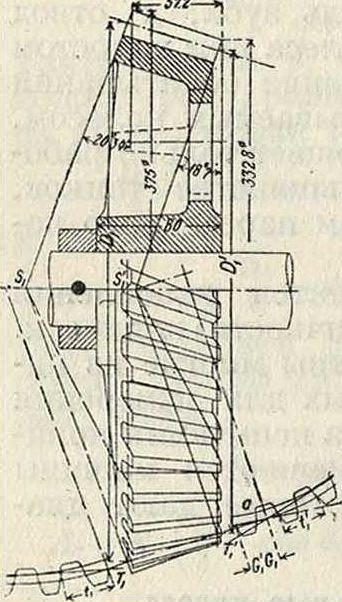
Фигура 42.

e₁t₁=2nVOF² · sin² δ_λ + a z₂t₂=2π YOF² · sin² <5₂ + a%,

τ,-τ,ν

OF² · sin² <5, -f a

OF² · sin² δ₂ + a|

что при OF=0 дает: γ cos <5_Χ=i₂ cos <5₂=t_n.

Фигура 42 дает конструктивный чертеж ги-перболоидалыюго колеса; длина зубцов по общей образующей FE делается не более 2 ί„. Расчетом, ,к-рый ведется по среднему сечению, как и. для конич. колес, определяется

1_п; допускаемые напряжения берутся вдвое меньшими, чем для соответствующих цилиндрических колес. Зубцы изготовляются отливкой или снятием стружки; в последнем случае обработка производится фасонными дисковым или концевым фрезерами. Вследствие трудности точного изготовления зубцов гиперболоидальные колеса ставят только в тех случаях, когда другое решение вопроса невозможно [^п].

IV. Винтовые колеса.

Винтовые колеса, решая ту же задачу, что и гиперболоидальные, не являются, однако, равноценными последним, т. к. все условия зацепления в них хуже, чем в гиперболои-дальных. Ценным преимуществом винтовых колес является легкость изготовления их. Наиболее простой переход от гипербо-лоидальных колес к винтовым, а вместе с тем сходство и различие между ними, можно установить, если гиперболоиды в жерловой зоне (фигура

41) заменить круглыми цилиндрами(фигура

43), которые будут ^ _ касаться друг друга г· в одной точке О. Со- g храняявсесоотноше- ^, ,

ния, указанные вы- ° Л ^фнг· ⁴³·

ше для точки О, получаем следующие основные соотношения для винтовых колес:

<5! + <5₂=<5; (1)

^ch + а₂=а ; (2)

i₁cos5₁= i₂cos<5₂= t_u ; (3)

j£ 2, a,cos <5₃ ^

ω₂ z_x a, cos

В отличие от гиперболоидальных колес, одну из четырех величин—а_и а₂, <5, и <5₂—можно выбрать произвольно, остальные определятся из вышеуказанных ур-ий. Профили винтовых колес—эвольвентные. Зубцы представляют собою винтовую нарезку одного направления, с углами подъема средних винтовых линий: β₁=90° — δ₁ и /3₂=90°—(5₂. Прямая ЕЕ—общая касательная к зубцам; скорость скольжения зубцов вдоль общей касательной: с=α_χω_χ sin + α₂ω₂ sin <5₂. Это скольжение является крупным недостатком винтовых колес, т. к. оно увеличивает износ зубцов и уменьшает их кпд. На фигуре 43 показано в плане такое колесо и схема сил, действующих на колеса. Пренебрегая трением вдоль профилей, получаем:

1) давление вдоль оси колеса 1

<Si=-Pitg (δ₁-ρ);

2) давление вдоль оси колеса 11

sin (й_гч-е).

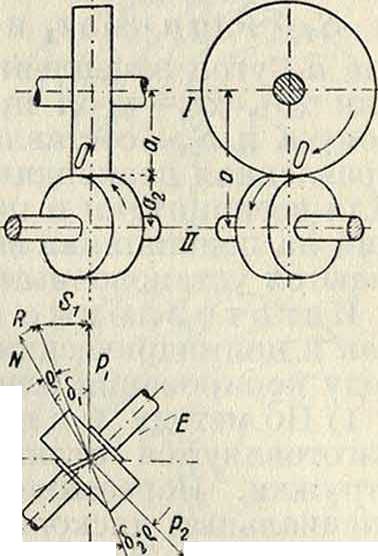
S₂=П sin (d₂ + f?)=Pi _{cos {Й1}3) окружная сила на колесе II

о) ’

P₂=D COS (<5₂ + ρ)=Pi

cos (й₂ + е)

cos (<5, - e)

В этих ф-лах Pi—окружное усилие на ведущем колесе 1, ρ—угол трения, D—давле-

ние на зубец, отклоненное от нормального давления N на угол ρ, причем

N=D-cosq ж D =

_Р,___

COS (<5, - ρ)

Коэффициент полезного действия

_ Р₂Р₂ _ Pja^H _ 1 tg£s ~ Λ»ι ~~ >ιβι<»; ~ ΐ + iig»_t ’

где /=tgo. Кпд зависит от угла наклона зубцов; при ι5ι=<5₂=2 ^он достигает наибольшего значения. По характеру изменения η установлено, что наивыгоднейшие пределы для (?!—от 30 до 60°, в которых значение η мало отличается от v_max. Подсчеты дают, при 5=90° и /=0,1, Vmax=0,82. Расчетом определяется t_n, причем допускаемые напряжения вследствие сильного скольжения уменьшаются вдвое по сравнению с таковыми же соответствующих цилиндрич. колес; ширина обода берется равной окружному шагу. Передаточное число не более 5. При больших передаточных числах переходят к червячным передачам. Материалом при малых скоростях служит чугун, при больших—сталь по фосфористой бронзе, причем стальное колесо является ведущим. Обработка зубцов ведется так же, как цилиндрических колес со спиральными зубцами. Вопрос о наименьшем числе зубцов, нарезаемых без подрезания, решается, как было указано выше для спиральных зубцов, при а,=15°, <5,=<5₂=45°, а=20°4513" и ζ,. =12; приуменьшении ζ.

ниже этого предела следует применять исправление [^п].

V. Червячная передача.

В простейшем виде червячная передача представляет частный случай винтовых колес, когда на малом колесе 1 число зубцов не более 5, а обычно равно 1, 2 или 3. Малое колесо представляет в этом случае обыкновенный винт—червяк—с числом г ниток, равным числу г_х зубцов; большое же колесо—обыкновенно евинтовое колесо с числом зубцов ζ₂=ζ. Обычно червяк является ведущим. Угол д между осями, как правило, равен 90°, а потому, как и для винтовых колес с углом <3=90°,

к=“-!=?-=- tg <5,=^R ctg β,

ω₂ г г ο I γ Ο r i

где =90°—<5_Х—угол подъема средней винтовой линии червяка, R и г—радиусы начальных цилиндров колеса и червяка. Если поставить ось червяка к плоскости колеса под углом, равным углу β, то колесо м. б. изготовлено в виде обыкновенного цилиндрич. колеса с прямыми зубцами, что и позволяет использовать червячный фрезер для нарезания прямых зубцов. Недостаток простейшей червячной передачи заключается в том, что зубцы червяка и колеса касаются в одной точке; такая передача пригодна только при действии небольших усилий или для передач, работающих с весьма длительными перерывами. Для улучшения условий зацепления зубцу и ободу колеса дается дуговое очертание "по фигура 44, А.

В червячных передачах пользуются исключительно эвольвентным профилем с углом зацепления а=15°. При нормальной высоте зубца /i=2,2т, где т—модуль, блого приятные условия зацепления получаются, если на колесе 2,„_г-»=3б, то есть при больших передаточных числах. Вследствие этого находит частое применение укороченный зубец с высотой /i=l,8 тонн (/i=0,25Zsi0,8 тонн и /i"=0,3i^m), при к-ром z_min=28. Если через ось червяка провести плоскость, перпендикулярную оси колеса, то в сечении с червяком получим эвольвентную рейку, а с колесом—эвольвентные профили цилиндри-ческ.,колеса (фигура 44, В). Начальная линия

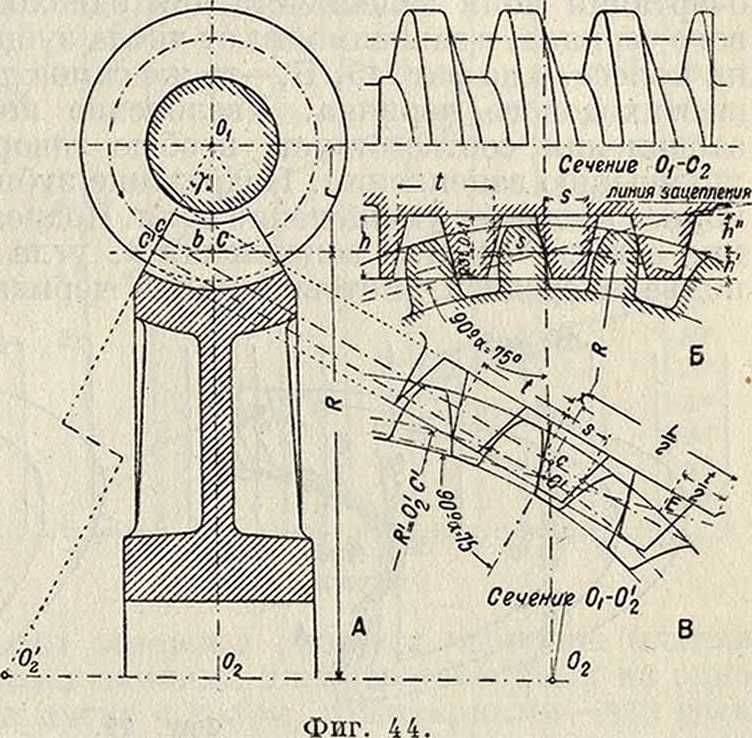
рейки и начальная окружность колеса определяют начальные поверхности червяка и колеса; поэтому цилиндр радиуса R называют начальным цилиндром колеса, а цилиндр радиуса г—начальным цилиндром червяка; тогда 2nR=zt, 11=it,

где Η—ход средней винтовой линии червяка, t—шаг зацепления рейки и колеса и β— угол подъема винтовой линии червяка. Приближенное очертание профилей для литых зубцов дается тем же приемом, как и для конич. колес,—вычерчиванием профилей на развернутой поверхности конуса с вершиной в (Ц (фигура 44, А). Указанный приближенный способ допустим только при небольших углах β и при ширине колеса Ь ^ 1,5 Ζ по начальной окружности червяка [“]. Совершенно точное получение профилей на зубцах колеса достигается нарезанием их по методу обкатывания червячным фрезером, профиль зубьев которого точно соответствует профилю нарезки червяка. Целесообразное назначение основных величин—числа зубцов на колесе и числа ниток на червяке, обеспечивающих благоприятные и правильные условия зацепления,—м. б. произведено только на основе подробного исследования зацепления между червяком и колесом. Методы такого исследования даны Эрнстом [²⁰] и Шибелем [^п].

Результаты исследования показывают, что: 1) в зацеплении участвует одновременно несколько витков червяка (2—3); 2) в любой плоскости, параллельной средней плоскости колеса, соприкосновение между витком червяка и сопряженным зубцом колеса происходит по определенной"линии, которая определяется построением; 3) совокупность таких линий определяет поверхность зацепления, которая зависит от червяка и не зависит от колеса; 4) линия пересечения поверхности зацепления с внешними поверхностями червяка и колеса ограничивает часть поверхности зацепления, называемую полем з а ц е и л е и и я [²,¹⁰, “]. Поле зацепления является характеристикой передачи. На фигуре45, А, даны, в проекции на плоскость, перпендикулярную к линии кратчайшего расстояния между осями червяка и колеса, очертания поля зацепления для одноходового червяка, в зависимости от числа зубцов на колесе, а на фигуре 45, Б,—то же самое для шестиходового червяка. Увеличение поля зацепления соответствует, вообще говоря, улучшению зацепления. Подрезание зубцов колеса вызывает уменьшение поля. Подрезание зависит от угла зацепления а, угла β, подъема средней винтовой линии червяка,

r-05f -J. D.5f

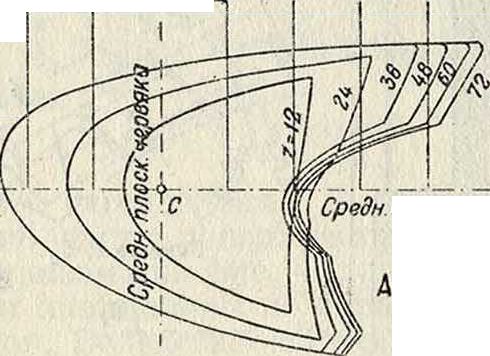
05t - 05ΐΛ

плоек.колеса

Фигура 45.

числа г ниток, передаточного числа к и высоты и формы головки червячного фрезера, нарезающего колесо. Особенно быстро возрастает подрезание при увеличении угла β и уменьшении числа ζ зубцов на колесе. Смещение червячного фрезера устраняет подрезание и позволяет правильно нарезать колеса с числом зубцов до 12 С¹⁰,¹¹]. Исследование зацепления позволяет правильно назначить длину L червяка в зависимости от числа ζ зубцов на колесе:

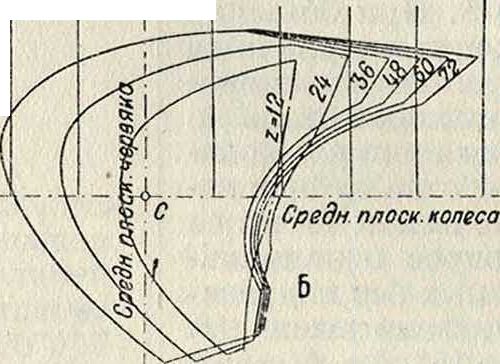
2=12 L 4

24 36 60 свыше 70

= 3,2 4,0 4,8 5,6 6

Материалом для передач, работающих с небольшой нагрузкой, служат: для червяка—чугун или стальное литье, для колеса—чугун. Необработанные зубцы применимы для скоростей скольжения до 2,5 м/ск. При более высоких скоростях червяк изготовляется из стали, тщательно обрабатывается и полируется, часто закаливается, после чего подвергается выверке и шлифовке. Для колеса в этих случаях применяется чугун, а при повышенных требованиях—фосфористая или алюминиевая бронза. Для удешевления из бронзы изготовляется только зубчатый венец, который надевается на обод чугунного или стального колеса.

Расчет. Рассматривая червяк и колесо как винт и гайку, можно выразить соотношение между силой Р, приложенной касательно к начальному цилиндру червяка, и силой Q, действующей вдоль его оси, в виде: P=Qtg (β + ej,

при чем tg ρ_χ=/i =, где /—коэфф. трения и а—угол зацепления эвольвентой рейки. Момент, вращающий червяк,

M=Qr tg (β + ρ,). Коэффициент полезного действия

«=—!?J—.

tg όί + ο,)

Фигура 46 дает зависимость η от β и д. При изготовлении червяков угол β обыкновенно берут не больше 18—20°, т. к. при больших углах ухудшаются условия зацепления; в крайних случаях β=30°. Из фигура 46 видно, что преобладающее значение для η имеет угол трения ρ. Средние значения ρ и /, принимаемые при расчетах:

е

Для чугуна по чугуну. .6—7° 0,1—0,12

» стали » бронза.2—3° 0,03—0,05

Меньшие значения предполагают весьма тщательное выполнение червяка и колеса, а также хорошую смазку. Принимая во внимание трение в опорах червяка и колеса, а также трение вдоль профилей зубцов, полный кпд можно выразить следующей формулой:

^Г,п· ⁼ Τ+φ

Согласно опытам, φ== 0,02 -г- 0,1, причем меньшие значения принимаются при тщательной смазке подшипников и при шариковых опорах. Установлено, что кпд передачи зависит от нагрузки, при которой работает передача, материала червяка и колеса, состояния поверхностей трения, смазки и скорости скольжения [¹⁰]. Наибольшее значение?? при обычных условиях работы равно 0,85. Низкие значения /и соответственно высокие значения η имеют место только при установившемся движении. Для передач, работающих с частыми перерывами, как в подъемных кранах, средняя величина η значительно ниже. Погрешность в шаге, а также в установке сказывается весьма чувствительным понижением η. Для β<ρ_χ получается самотормозящая передача, в которой передача вращения от колеса к червяку совершенно невозможна. Для предельного случая β=ρ^ η=* - A tg² β, τ. e. η < -¹-. При больших скоростях червяка коэфф. трения уменьшается благодаря улучшению смазки. Это позволяет иметь самотормозящую передачу с кпд до 70%, но за счет надежности действия в отношении самоторможения.

Расчет зубцов производится по тем же ф-лам, которые даны для цилиндрич. колес, то есть то=22 т/~—%г- или то=912 л/~

У <pzli_u. у где М—вращающий момент колеса (в к гем): ^

ζ—число зубцов на колесе; ψ= для обработанных зубцов—от 6 до 9, для необработанных—от 4,5 до 6; N—мощность на червяке (в Η⁵); η—кпд передачи; п—число об/м. колеса; то—в миллиметров; Квыбирается, в зависимости от окружной скорости червяка, по той же таблице, которая приведена для цилиндрич. 3. к. Теплота, развивающаяся при

Νη

<pznk„.

трении между червяком и зубцами колеса, не должна вызывать недопустимого повышения темп-ры масла сравнительно с температурой воздуха £„. По данным опытов Баха 1 ю

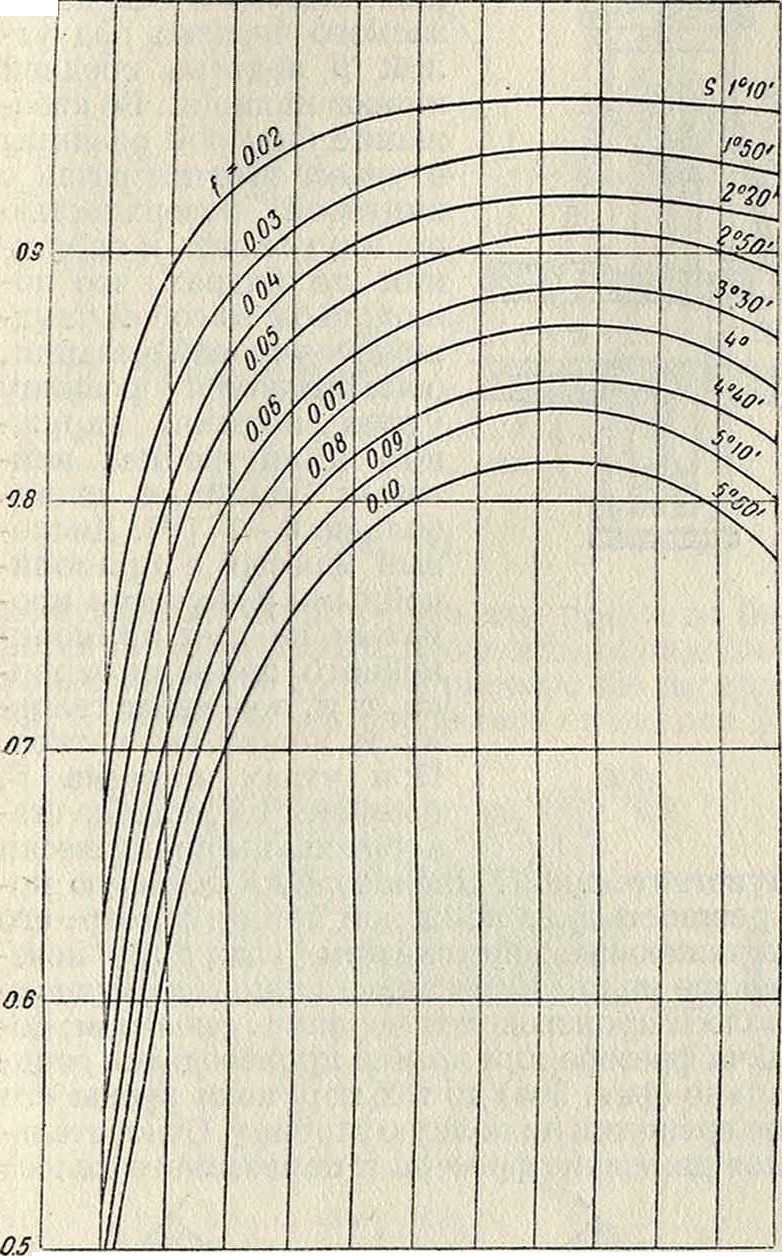
β=5° Ю 15 го 25 30 35 00 05 50 55 60°

ФИГ. 46.

и Розера, Брауном установлена зависимость допускаемого напряжения К_и- в зубцах колеса от разности позволяющая при проектировании производить проверку К_и. но данной величине t_M — и наоборот:

к„_=u(t_M. - и + В],

18

где

^=Ϊ5Ϊ + 0,42,Β=₅

109

- 2;

5, V

CKO-

2, 75 +v

рость на, окружности червяка, к_и,—напряжение материала колеса, соответствующее скорости v=A м/ск в таблице, приведенной для цилиндрич. колес. Для передач, работающих непрерывно, i_w< — t_6m — 50°; для передач, работающих с перерывами, t_Mί_β.==90° [⁹, ^u,¹³]. Для предварительного назначения η, необходимого для расчета т, могут служить следующие данные:

Число ниток

Значения η для червяка, выполненного в одно целое с валом 0,717 0,795 0,828 0,843

Значения η для червяка, надетого на вал 0,632 0,758 0,810 0,836

Диаметр вала червяка м. б. определен по крутящему моменту, учитывая изгиб понижением допускаемого напряжения на скручивание; при этом принимают: для стали к_кР=120 килограмм/см²; для стального литья к,_кр== 100 килограмм/см²; для чугуна к_К]),=30 килограмм/см²; соответственно этому получаем:

_сц=5= %·=3 000 ^N ; d*==

⁰ R-κρ· 24 η ⁷ ° 20

: 12 000

N

Μ,φ

g- _η

Толщина стенок полого червяка 0,5-f-0,6i. Па диаграмме, изображенной на фигуре 47,

Оа.

ш

		кпд г	ου f=0.	05 φ°0	02
-				^А	8uVs
____
1								J*-
					угол^	0Эт>е"	I

30°

25°

Ю°

5°

I- 2 3 0 5 в 7 8 9 Ю

ФИГ. 47.

даны основные размеры червяков (сплошными линиями для изготовленных из одного куска с валом, пунктирными—для насаженных). Размеры чугунного или стального колеса, на которое надевается бронзовый обод, определяют по правилам, изложенным

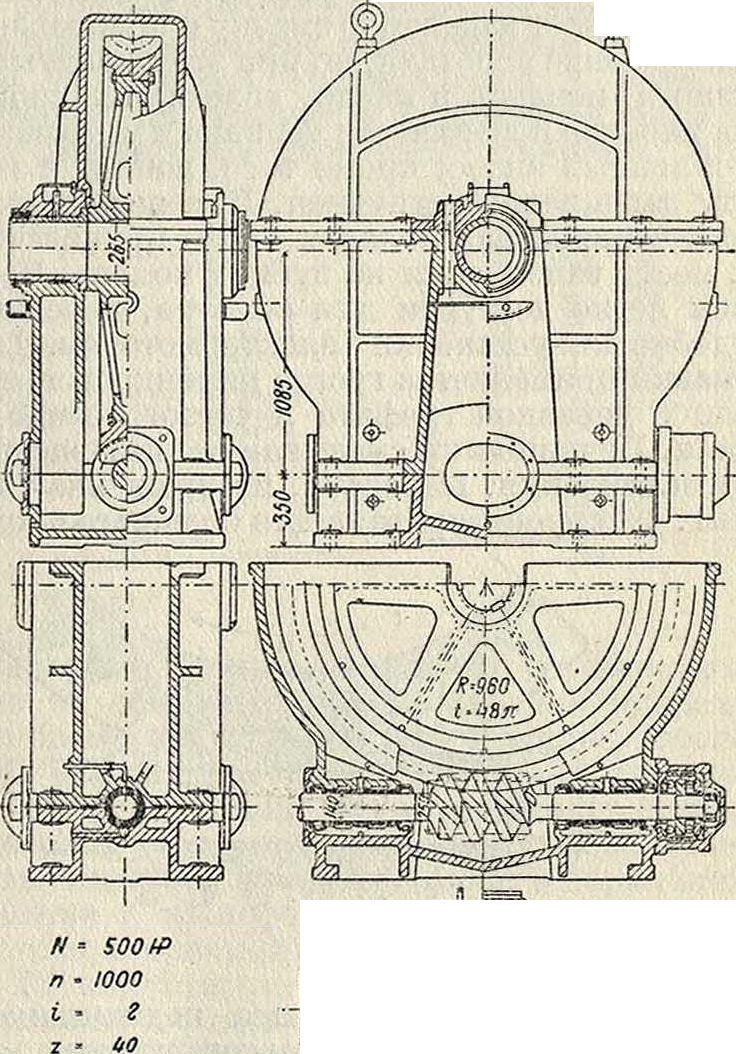
		» II»	m
	1 !		j
	ί i		1
		4 о 1	л)

Фигура 48.

для цилиндрич. колес. Закрепление бронзового обода на чугунном производится или точно пригнанными болтами (смотрите фигура 48),

работающими на срез, или же оронзовыи обод насаживается на гладкий обод чугун, колеса под прессом или в нагретом состоянии (фигура 49). Точная установка относительного

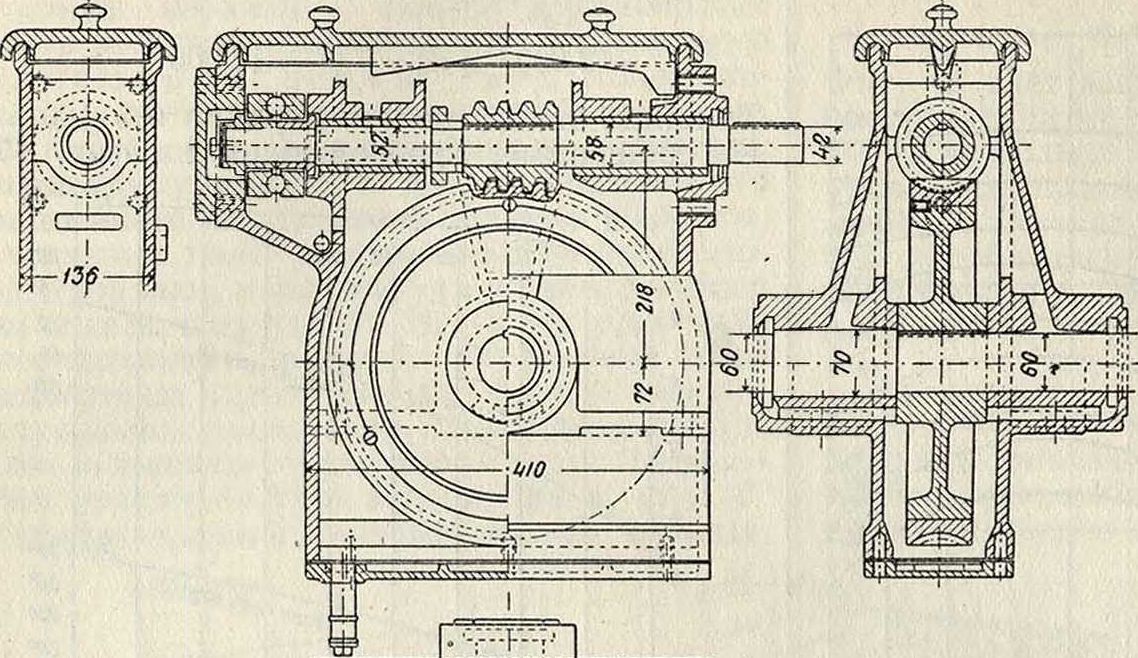
	О:	ж	iO	b=1
АП	Jk.ll	jj	п:

Фигура 49.

расположения червяка и колеса достигается заключением их в общий чугунный кожух, который служит также резервуаром для масла, смазывающего передачу, и защищает ее от пыли. При расположении под колесом (фигура 48) червяк всегда работает в масле, что обеспечивает надежную смазку и прекрасное охлаждение передачи, но при этом продукты износа, попадая в масло, увлекаются снова на рабочие поверхности червяка и вызывают усиленный износ; кроме того, доступ к месту зацепления затруднен. При расположении червяка над колесом масло приносится к месту зацепления на зубцах колеса. Червяк легко доступен для осмотра, передача удобна для установки с электромотором. Для смазки применяется густое цилиндровое масло с добавкой графита и чистого свиного сала. Подшипники смазываются независимо от зацепления. Передача, изображенная на фигуре 49, спроектирована для большого числа

	—
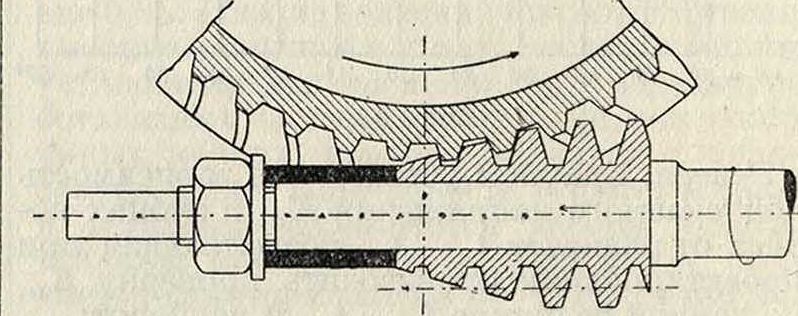
	г--!			(Л
	1_1			1
				—V-7

Фигура 50а. оборотов; при этом смазка подшипников как червяка, так и колеса совершается маслом, разбрызгиваемым червяком. Осевое давление червяка воспринимается обычно шариковыми подпятниками.

Точное изготовление червяка достигается применением резца, режущая кромка которого представляет очертание прямолинейного зу ба эвольвентной рейки с углом зацепления а„=15° и модулем ж„, соответствующими нормальному сечению нарезаемого червяка. Плоскость резца совмещается с нормальной плоскостью, то есть устанавливается к оси нарезаемого червяка под углом β подъема средней винтовой линии. Во избежание большой разницы в углах заточки резца с винтовой поверхностью на внутреннем и наружном цилиндрах, что повлекло бы за собой ухудшение условий резания, рекомендуется разницу углов подъема наружной и внутренней винтовых линий не делать больше 6—7° [^п]. Дисковый фрезер с прямолинейными режущими кромками не дает прямолинейного профиля червяка, т. к. подрезает головку и ножку его витков. При углах подъема β, больших 10°, ошибка становится уже практически чувствительной. Значительно меньшую погрешность дает концевой конич. фрезер, его искажающее действие при углах β<20° исчезающе мало. Нарезание зубцов червячного колеса производится червячн. фрезером; подача фрезера или колеса производится радиально (фигура 50а) до тех пор, пока зубцы его не врежутся на полную глубину. Относительное движение фрезера и нарезаемого колеса

Фигура 506.

таково, как будто они находятся в зацеплении. После врезания на некоторую глубину вращение колеса производится самим фрезером. При углах подъема фрезера больших 6° радиальная подача вызывает порчу зубцов колеса и заменяется поэтому тангенциальной подачей (фигура 506). Передние по направлению подачи витки фрезера срезаны, и он получает вид конуса. Преимущество тангенциальной подачи состоит в том, что зубцы фрезера врезаются в заготовку постепенно; последние витки только зачищают обрабатываемую поверхность, которая получается гораздо чище, чем при радиальной подаче. Однако, и в этом случае вновь изготовленное колесо должно приработаться к своему червяку, прежде чем передача начнет работать безупречно.

Особый вид червячной передачи представляет глобоидальная передача (фигура 51а). Червяк и колесо представляют собою тела вращения—глобоиды, образован-

ные вращением дуг ЛОВ и CAD соответственно около осей 1-1 и 11-11. Глобоидальный червяк (фигура 516) м. б. нарезан резцом,

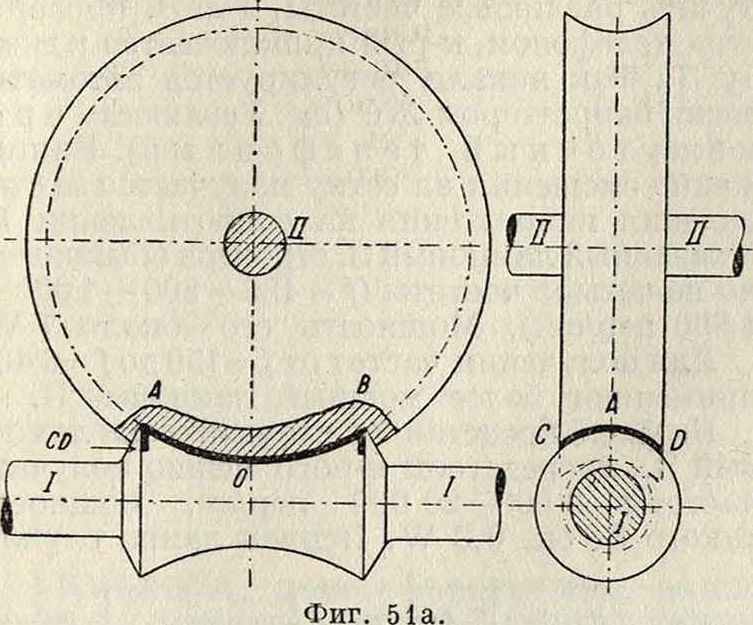
режущий профиль которого для простоты берется прямолинейным; плоскость резца должна совпадать со средней плоскостью передачи, и резец должен вращаться около оси 11

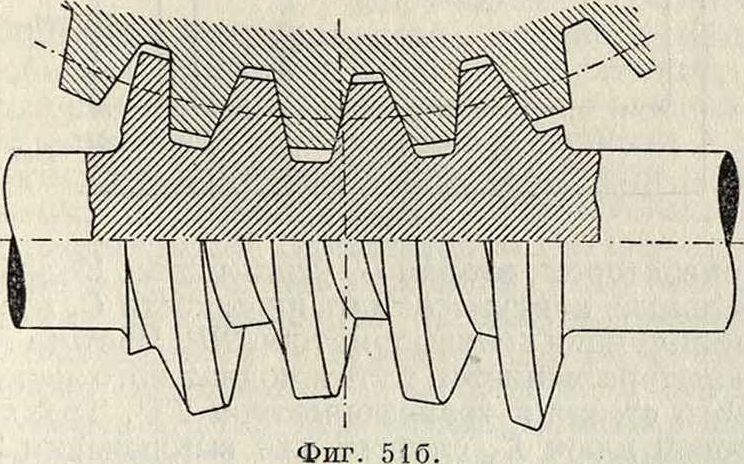
колеса. Глобоидальное колесо должно нарезаться глобоидальным фрезером, точно соответствующим червяку. Сложность последнего инструмента и недостатки его при резании приводят к приближенному выполнению глобоидального зацепления, к-рое в работе дает,однако, вполне удовлетворительные результаты [^п]. Для уменьшения трения герм, машиностроительный з-д Пекрун

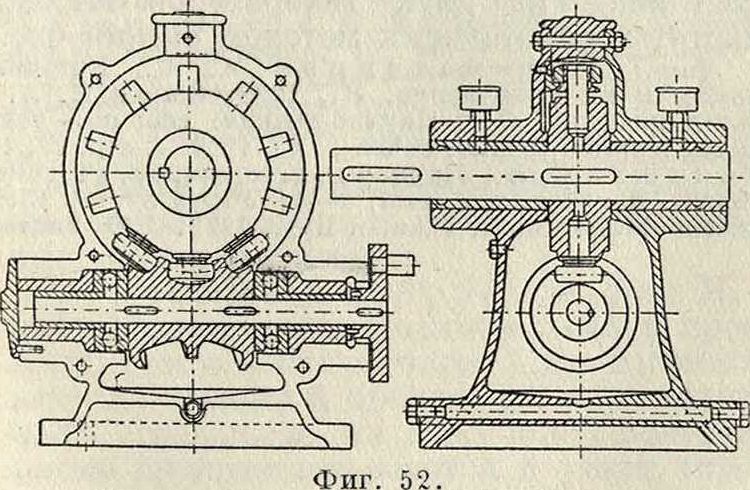
(Козвиг) заменяет зубцы глобоидального колеса роликами и соответственно этому выбирает профиль нарезки глобоидального червяка (фигура 52).

Лит.: ‘)Зернов Д. С., Прикладная механика, ч. 1, Л., 1925; ^s) Б е р л о в Μ. Н., Детали машин, вып. 4 и 5. СПБ, 1909—10; ³) Рерих К. Э„ Кон спект по прикл. механике, П., 1918 (литогр.); *) Б о-б а р ы к о в И. И., Детали машин, часть общая, М. — Л., 1926, Часть специальная, М. — Л., 1927; ⁵) Ш и б е л ь А., Зубчатые колеса, пер. с нем., СПБ, 1913;*) Сидоров А. И., Детали машин, ч. 2, М.—Л., 1926;) «Известия СПБ политехнич. ин-та», СПБ, 1913, т. 19, стр. 205—306; *) Меламед И., Наладка зуборезных станков и работа на них, М.—Л., 1927;⁸) Bach С., Die Maschinenelemente, В. 1, Lpz., 1922; ¹⁰) R б t s с h е г F„ Die Maschinenelemente, В. 2, В., 1929; “) Sehiehel A., Zahn-rador.Einzelkonstruktioncn aus d. Maschinenbau, hrse. v. H. Volk, H. 3, B., 1922, H. 5, B., 1923;^1!) H a rt-та η n W., Die Maschinengetriehe, Stg.—B., 1913; ¹³) Η 6 η n i c k e G., Die Teilung d. Zahnrader u. ihre einfachste rechnerische Bestiinmung, B., 1927; “) Barth C., Die Grundlagen der Zahnradbear-beitung, B., 1911; “) К ut z 5 a ch K., Grundlagen u. neuere Fortschritte d. Zahnraderzeugung, B., 1925; ^IS) Kruger P., Die Satzradersysteme d. Evolven-tenverzahnung, B., 1926;¹⁷) Berndt G., Zahnrad-messungen, Erfurt, 1925; ^1!) Versuchsergebnisse d. Ver suelisfeldes f. Maschinenelemente d. Techn. Hochschule zu Berlin, H. 3 — 4, Mch. — Berlin, 1923; ’*) Go 1-liasch K., Die Ermittelung d. Kegelrad-Abmes-sungen, B., 1923;²°) Ernst, Die Hebezeuge, В. 1—3, 4 Aufl., B., 1903; ²¹) «Mechanical Engineering», N. Y., 1926, 11; ²²) «Machinery», 1925, p. 197; ²³) «Maschi-nenbau», B., 1923, p. 623, 1924, p. 159—163, 1926, p. 402—406,1928,p. 675—678; ²ⁱ) «Werkstattstechnik», В., 1924, p. 75—98, 169—173; ²ⁱ) «American Machinist», London,1926, 8, 10—16, 18—25;^ы)«Werkstatts technik», Berlin, 1924, p. 121 —135; =⁷) ibidem, P. 135—141; “) «BBC Mitteilungen», Baden (Schweiz), 1926, 3—6. X. Кетов.