> Техника, страница 48 > Изгиб

Изгиб

Изгиб, один из видов деформаций, характеризуемый тем, что поперечные сечения стержня, первоначально параллельные, при деформации наклоняются друг к другу, причем ось стержня искривляется.

Прямолинейный стержень. На фигуре 1 изображен в деформированном состоянии стержень, первоначально прямой.

1-й случай (круговой изгиб). Выделенный по длине стержня участок подвергается действию изгибающего момента М (фигура 1).

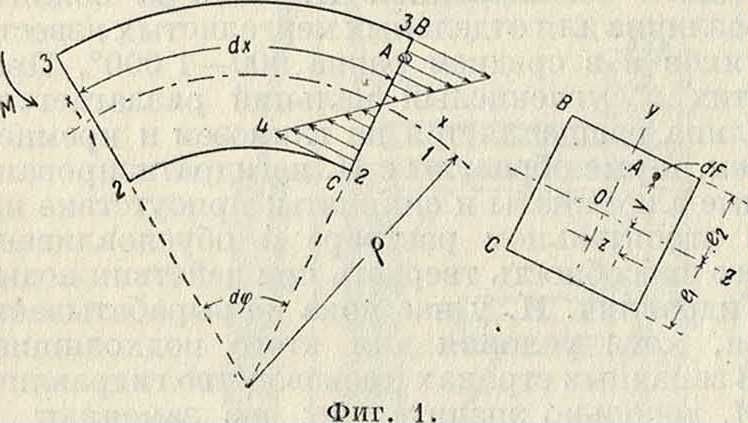
Пограничные волокна стержня испытывают деформации: 3-3—растяжения и 2-2—сжатия, причем можно найти такой промежуточный слой 1-1, волокна которого не изменяют при изгибе своей длины.Этот слой называется н е fi-трал ь и ы м. На фигуре 1 сечение этого слоя с плоскостью чертежа представлено линией х-х. Предполагается,что изменение деформаций по высоте сечения (ось Y) происходит по прямой 4-4 (гипотеза Навье). Поэтому деформация в некоторой точке A {z, у) сечения равна

d)

где г_в—наибольшая деформация, получающаяся в краевом волокне В сечения. Далее предполагается, что между напряжениями и деформациями при И. существует прямая пропорциональность (закон Гука):

К_А=Ei а

(2)

где Е—модуль упругости 1-го рода. Из геометрических соотношений фигура 1 получим:

_ Гд £.4 __ (ρ 4- У) d φ — Q(i<p

^г А ~

У

и где I

-г -, (3)

д еа<р е

•длина волокна А после деформа ции, 1_А—длина волокна А до деформации. Напряжение в той же точке

d)

при чем q—радиус кривизны нейтрального волокна, деформация которого равна нулю. Т. о., напряжение в любой точке сечения определяется ее расстоянием от нейтральной линии и радиусом кривизны последней. Положение нейтральной линии и радиус кривизны находим из условий равновесия выделенной части стержня.

1) Сумма проекций на любые направления всех действующих сил равна 0:

F F

J к_г dF=0 или J Е - dF=0, (5) о о®

откуда

F

j у dF=0 ; (6)

о т. о., статич. момент площади сечения относительно нейтральной линии равен 0—нейтральная линия проходит через ц. т. сечения.

2) Сумма моментов всех сил относительно любой оси равна 0:

а) относительно оси Z

F F

j к. · у dF=- · J* if dF=Μ, (7)

о ⁸ о

F

где J у² dF=I,—момент инерции площа-о ди сечения относительно оси Z. Из уравнения (7) имеем:

(8)

i _ м е ~~ Ε·Ι_Ζ ’

то есть кривизна нейтральной линии равна изгибающему моменту, деленному на жесткость (Е Ι_ζ) балки при И.; б) относительно оси Υ

F F

J k_z · z · dF — 0 или J z у dF=0 ; (9) о ⁸ о поэтому

F

fy-zdF=I_yl=0, (10)

о то есть центробежный момент площади сечения относительно нейтральной линии равен 0, и оси Y и Z—главные центральные оси сечения. Сопоставляя выражение для радиуса кривизны и напряжения, получим:

к, л —

^ZA

Му

17’

и для краевой точки сечения

(И)

к

^гв

Me.

17’

(12)

где е₂—расстояние от нейтральной линии наиболее удаленного волокна. Обозначая через -=W_z момент с о п р о т и в л е-

е₂

и и я. имеем:

^.-5· ds)

у p-и е прочности, по к.-рому при выбранном допустимом для данного материала напряжении на изгиб к_ь отыскиваем прочные размеры балки в том случае, когда напра-

вление действующей силы совпадает с одной из главных осей сечения.

2-й случай. Все действующие силы приводятся к моменту и главному вектору сил; в этом случае условия равновесия дают при малых углах dip (фигура 2):

-M + S₁dx + М₁=0, (14)

где М—изгибающий момент в сечении I, M_t—в сечении II, отстоящем на бесконечно малое расстояние dx. За положительное направление момента принято то, которому соответствует вращение по часовой стрелке. При М > М_х

dM=M-M₁=S₁dx,

или

(15)

с _ <^т

- ~хг ’

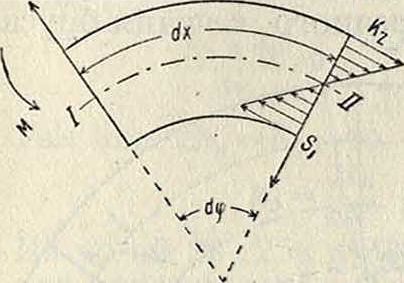
Фигура 2.

то есть главный вектор сил является производной изгибающего момента по х (теорема Шведлера) и называется срезывающей силой. Момент М_х компенсируется теми я-te нормальными напряжениями /с₃,как и в случае отсутствия главного вектора. Существование последнего обусловливает появление напряжений касательных, лежащих в плоскости сечения. Т. о., в каждой точке балки действуют касательные и нормальные напряжения. В длинных балках, в которых отношение длины I к высоте h (или диаметру балки d) больше 10, преимущественное значение имеют нормальные напряжения; расчет ведут по формуле: ^

Т 7 _ ^ wax

^г Ч

В коротких балках (*=~ < ю) следует делать проверку на касательное напряжение. Деревянные балки, благодаря слабому сопротивлению дерева сдвигу, обязательно должен быть проверены на касательные напряжения. Клепаные железные балки также должен быть проверены на касательные напряжения т. к. площадь сечения их вообще мала и легко моясет оказаться недостаточной по отношению к касательным напряжениям. Ур-ием (8) устанавливается зависимость меледу ординатой прогиба балки и изгибающим моментом в данном сечении, именно

&у

1 dx² М

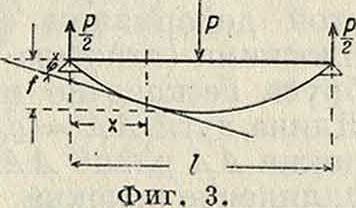
При незначительных углах у, образуемых изогнутой осью балки с осью×(фигура 3), можно принять, что

1 ₌ (Г-1, о dx² ’

и дифференциальное ур-ие упругой изогнутой оси представится в таком виде:

<Е. i .ίΣ ₌ Μ

^z dx^{2 τ}·

(16)

прогиба в функции х. Подстановкой любого значениях определяется стрела прогибав точке с абсциссой х. Интерес представляет всегда наибольшая стрела прогиба, которая бывает в середине однопролетной балки или вблизи середины.

Частные случаи. 1) М^.=Const, т.е. изгибающий момент постоянен. По ур-ию (16) и (8) следует, что ρ=Const, или изогнутая ось балки представляет собой дугу круга. Стрелу прогиба получаем геометрически: для консольной балки

=

мг

2E-I,

2) М_х= ₂ х (фигура 3). Ур-ие изогнутой оси: откуда

η т <Py Р

•® dx* ^— 2 ^Х’

Е I_z ~ + С,

¹ dx 4 ¹ ’

E I. у=+ Сх + С_х.

При ж=0: у= 0 и C₁= 0; при ж= ₂:

Двукратное интегрировапие даст ординату и С — — Поэтому

РР ιβ ‘

„ _т Рх> РР

^Е Iz · У=То -тг“.

При х =,

=

12 Р1³

А8Е- I_z

3) При одновременном действии сосредоточенных сил и равномерно распределенных нагрузок количество постоянных в уравнении

Рг да“

.1

Фигура 4.

Г

Фигура 5.

ошп упругой кривой увеличивается на две для каждой области, и нахождение их, в виду сложности ур-ия, представлялось бы затруднительным. Число постоянных для всех случаев сосредоточенных и сплошных нагрузок, по теореме Клебша, м. б. сведено к двум. Для балки (фигура 4) количество постоянных, подлежащих определению, равно двум; обе постоянные легко отыскиваются из выражений для конечных условий: а) у=0 при х=О и б) у=0 при х=1. К балкам (фигура 5) теорема Клебша неприменима, так как в этом случае равномерно распределенная нагрузка, не сплошная.

Косой И. Косым И. будет, если направление действующей силы не совпадает с одной из главных осей сечения. На фигуре 6 направление силы совпадает с осью У, a Z₀— соответствующая главная ось 2-образного сечения: оси У и Z₀ образуют угол у. Разложением силы по главным осям Ζ₀ и У₀ явление косого И. может быть сведено к И. в двух главных плоскостях—ΧΥ₀ и ΧΖ₀—под действием моментов

М_го =Р1 sin у=М₀ sin у и М_Уо=М₀ · cosy. Напряжение в точке к (у₀, z₀)

_{/iV =}. ^М:>У^г° ₎

1_г

^лУо или

(17)

V Ч h.

где 2,₀ и 1_Уо — моменты инерции относительно главных осей сечения. Наибольшее на

Уо У

I

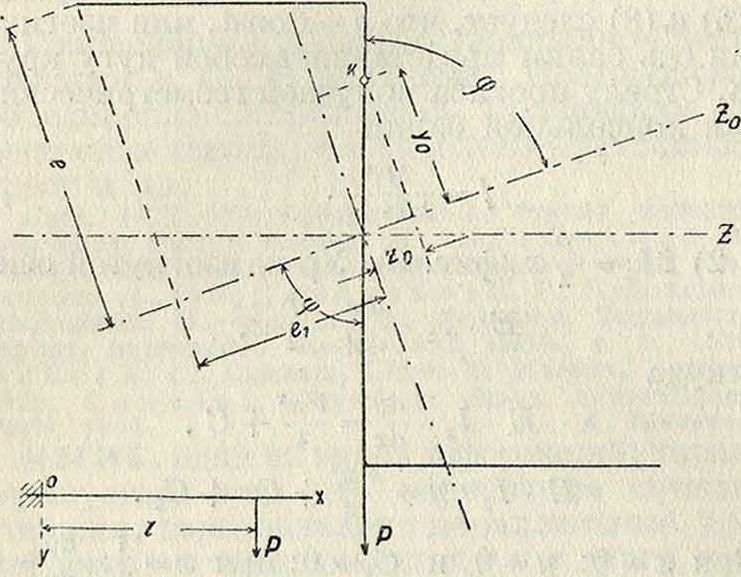
Фигура 6.

пряжение в сечении оказывается в крайних его точках (например при у_и= e п z₀=ej и равно:

к,_тх=М₀(^ + Щ^у (18)

Нулевое напряжение будет в точках, для которых

Уо · sin φ, Ζ₀ COS φ _,

τ. "τ ; ^υ >

или

У ο -

Ctg φ.

(19)

τ. е. все точки с нулевым напряжением лежат на одной прямой, положение которой зависит от относительного значения главных моментов инерции сечения и расположения силы по отношению к главным осям сечения.

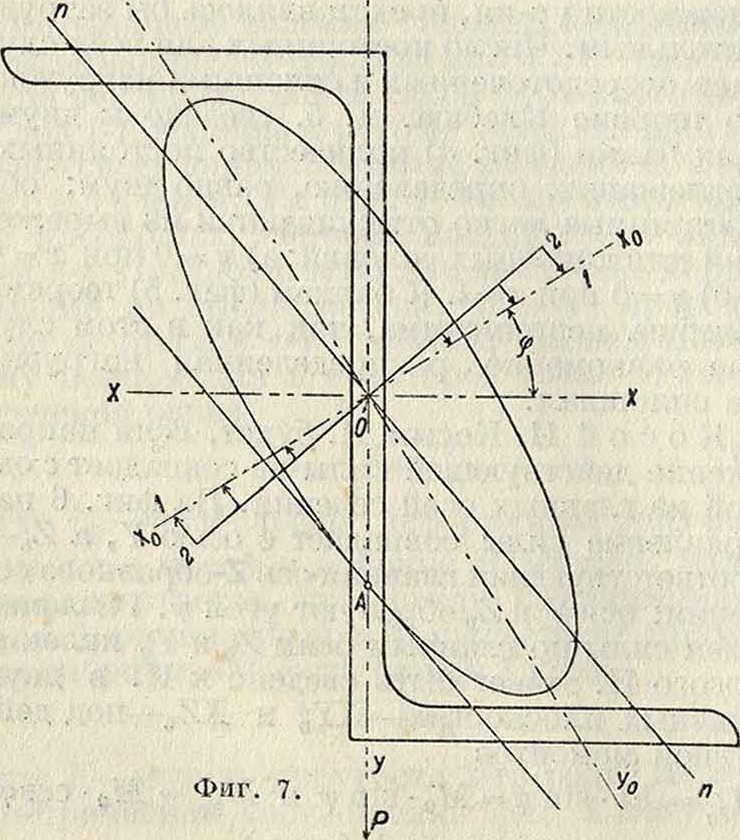
Нейтральную линию при косом И. легко найти построением. Построив эллипс инерции (фигура 7), проводим в точке А пересечения контура эллипса с направлением силы касательную к эллипсу и через центр сечения параллельную ей: это будет нейтральная линия пп, соответствующая ур-иго (19). Тр-к 0-1-2 изображает распределение напряжений. Расчетное ур-ие (18) для косого И. служит .тишь для проверки напряжений в сечении: размеры сечения выбраны уже заранее по конструктивным соображениям или определены предварительно на тех же основаниях, что и в случае изгиба в главной плоскости.

Криволинейный брус. При рассмотрении брусьев, ось которых представляет плоскую кривую, обычно предполагают, что все впеш-ние силы лежат в плоскости кривизны и что в той же плоскости лежит одна из главных осей инерции поперечного сечения бруса. с

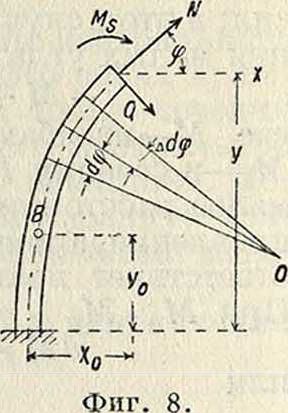
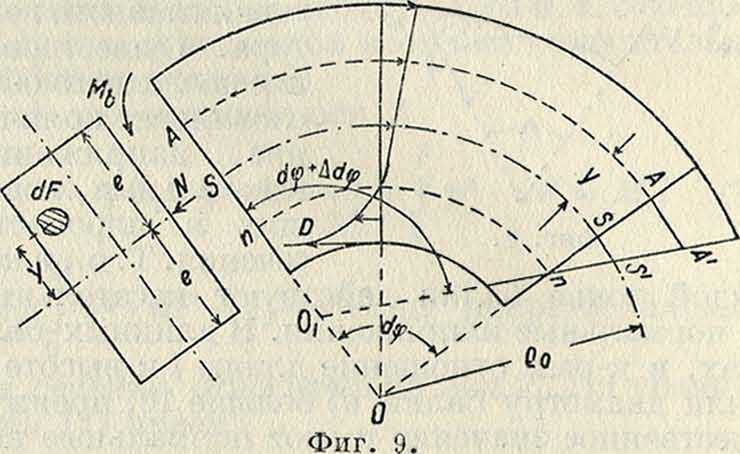
Брус, находящийся под действием сил, рассекаем плоскостью, перпендикулярной к изогнутой оси, и рассматриваем условия равновесия одной части. Внутренние силы взаимодействия отброшенной части можно привести к результирующему моменту M_s и силам N и Q (фигура 8). Силы Q (срезывающие силы) во внимание не принимают, полагая, что при этой деформации сечения бруса остаются плоскими (гипотеза Бернулли). Выделим из бруса бесконечно малый элемент (фигура 9). Длина дуги А А=(ρ₀ + у) d<p. Удлинение волокна АА равно AA=y dq>+SS, где SS— удлинение волокна, проходящего через ц.т. Относительное удлинение волокна АА будет г=_ aja

^у (e₀ + y)d<p ~ (e„ + y)di> ’

или с некоторой погрешностью где г₀—относительное удлинение волокна, проходящего через ц. т. Напряжение в той же точке А

Е · у A dv>

fc_z — Ei о -f-

(22)

0« + У dip

Распределение напряжений происходит по гиперболе и показано на фигуре 9 кривою CD. Из условий равновесия следует, что F

Jk„-dF~N, (23)

к₃ у dF=М_ь

(24)

Подстановка значения /г, дает: F F

Еу · Δάφ

о о

Ei₀F

Е · Αάφ г“ у dF

~d<p J ρ₀ -f- у О

iV

_Sm>yaF + SEt~-:*~v--Mb

0 Так как	0
F J* у dF=0 и 0	-!‘~dF -« Г fv-.M- €>о г V J V Оь + У,
то F	F.

SE

о или

Ααφ

у dF —	J 0	- if О И -* С (i><, + y)d<p
		F
• Λ άφ	Qo	с у dF
άφ		J во + υ О
% ~ К j	, то
k0 —	Mb л. IP	+ -· ‘ 7?

’ dF=М„, (25)

- - -

(25а)

^z F ⁺ c,F

(256)

Из ур-ий 22, 25а и 256 получаем выражение для напряжения в любой точке:

м ь у____

или, что то же,

и _ Я I ^МЛ, Μ» !

^г F ^ e.F ¹ (е,+ !/)>,/·/! ’

F

(26)

(27)

где

Тс

У dF

Значение к можно найти для каждого сечения графическим путем (по Толле) или разложением в ряды.

Для прямоугольника

‘-ί(ϊ)·+·ί(ϊ)·+·Η·3·+-

Для круга

Для трапеции

• {[ь₂ + V («. + е.)] ш - (h - &₂)}.

Здесь е означает половину высоты сечения, У— ±е для крайних волокон, в которых напряжение достигает наибольшего положительного или отрицательного значения.

Предлагают рассчитывать кривые брусья также по формуле Фёппля (Foppl):

(28)

то есть на сложное сопротивление; например, крюки, рассчитанные по этой ф-ле, обнаруживают далее излишнюю прочность. Нейтральная линия перемещается от ц. т. сечения по направлению к центру кривизны О, и это перемещение возрастает с уменьшением отношения —. Кривые брусья, для которых -^^5,

k _ ^N + «»

* ~ F ⁺ W- ’

рассчитывают по формулам сложного сопротивления для прямолинейных балок (брусья малой кривизны). Брусья, для которых < 5,

называются брусьями большой кривизны; их следует рассчитывать по ф-лам, выведенным для криволинейного бруса.

Деформация кривого бруса. Для определения перемещений отдельных точек кривого бруса под действием внешних сил удобнее всего пользоваться теоремой Ка-стильяно; для этого нужно иметь выражение потенциальной энергии бруса в виде функции от внешних сил. Возьмем точку криволинейного бруса В(х₀, у„) в первоначальном положений. После деформации ее положение будет А (х, у). Необходимо узнать приращения Ах и Δу координат и угол поворота Αφ в точке В. В общем случае на сечение бруса будут действовать изгибающий момент и продольная сила. Найдем выражение потенциальной энергии. Момент М вызовет приращение угла άφ на величину Αάφ, определяемую ф-лой д д,„ _ Medf

и совершит работу

άφ =

dT —

М 4 άφ

M‘_ds ‘ 2 Ε1·

Потенциальная энергия при действии одного момента будет

У р М^г ds

’ ~ J 2Е1_г

Продольная сила N изменит угол άφ на величину, определяемую ф-лой

λ Νάφ

^{Δ d(}P ~ ρ~ EF

При этом приложенный ранее момент совершит работу

dT_x - Μ Αάφ - ·

Продольная же сила создает потенциальную энергию:

т ₌

2 ~ 2EF

Полная потенциальная энергия под действием момента и продольной силы будет у __ р M*ds, р МN ds rN*ds

^V ~J 2EI_Z J EFq~ J ~2EF

Для брусьев малой кривизны это уравнение упрощается, т. it.

с MN , _п

f EFq ^db ~ ® ·

Б. ч. при решении задач пользуются ф-лой

У _ р М^г ds

^у ~ J YWiJ

Интегрирование распространено навесь брус. Искривление бруса будет вполне определено, если для каждого поперечного сечения известны перемещения его ц. т. и угол поворота.Положим,требуется исследовать деформации бруса, закрепленного нижним концом (фигура 8). Чтобы найти угол поворота сечения под действием внешних сил, нужно к заданным нагрузкам присоединить фиктивный момент т, приложенный в рассматриваемом сечении, и составить производную от потенциальной энергии бруса по т. Ур-ие потенциальной энергии выразится:

у, р (M + m)Nds pN‘ds

J 2Ё1 Г " EFq > J Wf

Возьмем части, производную по фиктивному

Δ,-βη

дт) ч моменту, полагая последний в окончательном результате равным нулю. Тогда

.o-/ir + /w~ ⁽²⁹⁾

Обычно приближенно принимают

^Α^Ιΐ£· (30)

Чтобы найти перемещение данной точки в направлении оси ж, нужно к заданным нагрузкам присоединить фиктивную силу X. Вследствие этого изгибающий момент в произвольной точке В увеличится на М_х==Х(у₀—у),продольная сила—наN_x=Xcos<p. Выраягение потенциальной энергии будет

V ₌ Г + Х(Уо -в)]* ds,

J 2jL· I %

I pfM + X(y_n - y))(N +×cos <p) (is. n(N+Xcos<p)·ds J EFq ^H J 2EF

Составляя частную производную по×и полагая в окончательном результате Х=0 (при чем средним членом пренебрегаем), получим искомое приращение:

i I дх I

.о"

(,Уо - у) Mds

Eh

+

Ndx. TSF ’

аналогично находим:

(х₀ - х) М ds

by о — J-

EI_Z

, n Ndy

"^r J ~EF

(31)

(32)

Оставляя вне внимания влияние нормальной силы, к-рое обычно невелико (3-1-4%, если действие момента оценить в 100%), получим более простые ф-лы:

^Ах°⁼ Ш7 ~ У)^ds

&Уо=— -γγ- J М (ж₀ - ж) ds

Все формулы применимы и к прямолинейным брусьям, причем для последних ds=dx. Выраягения для деформации (30), (31) и (32) можно охватить общей формулировкой: чтобы найти относительное перемещение двух точек криволинейного бруса в известном направлении, следует в одной из них приложить силу, равную единице, по направлению искомого перемещения и составить изгибающий момент от этой силы для произвольной точки бруса. Произведение момента этой силы на изгибающий момент в той яге точке от действительных нагрузок бруса представляет подинтегральную функцию дуги кривой. Интеграл этой функции, разделенный на жесткость бруса, дает искомое перемещение. Интегралы легко могут быть вычислены графическим путем.

Лит.: Худяков П. К. Сопротивление материалов, 5 издание, М., 1926; Тимошенко С. Н., Курс сопротивления материалов, 8 издание, М.—Л., 1929; БоС арыков И. И., Сопротивление материалов, 2 пзд., ч. 1, М.—Л., 1929; F б р р 1 A., Tcehn. Mechanik, В.—Lpz., 1924; В а с li С. u. Baumann R., Elastizitat и. Festigkeit, 9 Aufl., В., 1924; Μ о τι е у А. Strength of Materials, L., 1924; С 1 e b s c h A., Resum6 des lemons, Paris, 1888; Mayer, «Zeit-schrift f. angew. Mathematik u. Mechanik», B., 1926, B. 6, Heft 3. С. Лебедев.

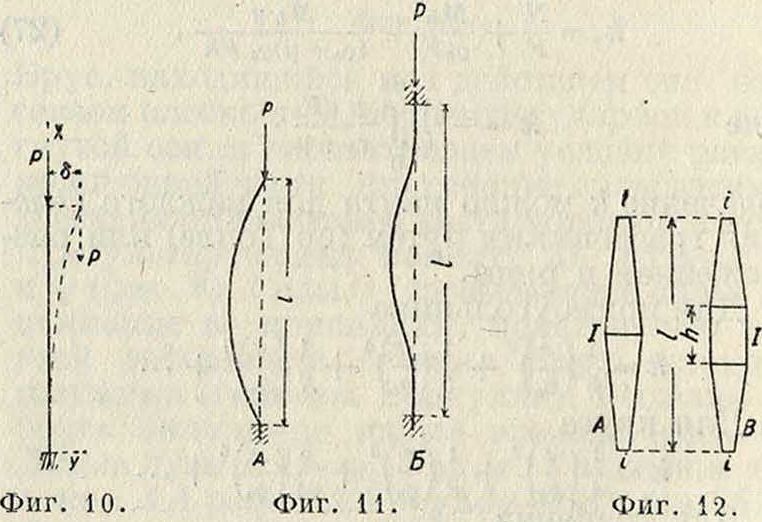
Изгиб продольный—искривление оси стержня под действием продольных сжимающих сил. Если вертикальный стержень постоянного сечения с нижним зажатым и верхним свободным концами сягимать силой Р, то при постепенном увеличении силы Р можно достигнуть предела, когда прямая форма равновесия стержня сделается неустойчивой и стержень изогнется (фигура 10). То значение Р,

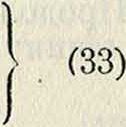
при котором начинается искривление, называется критической силой. Величину Р_кр. можно найти, пользуясь ур-ием И. Для случая, изображенного на фигуре 10, ур-ие упругой линии будет

EI -g + Py-Pi-O. (1)

Общий интеграл этого ур-ия:

у=A cos аж + В sin ах + <5, (2)

где а

Постоянные А и В определя ются из условий на концах изогнут, стержня: при х=0 :

1)К=0и2)к=0;

при х=I:

3) У =<5.

Из первых двух условий имеем А=— <5;

[ — Аа sin ах + Ва cos ах] _х=0=0, или В=0. Следовательно у=δ (1 — cos аж) удовлетворение третьего условия требует, чтобы

cos al =0, т. e. al =

(2π+1)π

и Р =

(2 п + 1)^гтг ^гЕ1 4Ϊ*

Наименьшее значение Р, при котором Ha-

7, л‘Е1

чинается искривление стержня, Р_кр, — ~ф

Подобным яге образом для стержня с обоими опертыми и обоими заягатыми концами (фигура 11, А и Б) имеем соответственно:

Р,

кр. л^гЕ I

~1^г

И

Р _.

(3)

Рассматриваемая задача поставлена и разрешена Эйлером, поэтому Р_кр. называется часто эйлеровой критической силой.

В случае стерягней переменного сечения I в ур-ии (1) является ф-ией ж. Во всех случаях критическая сила может быть представлена формулой

КЕ1

1‘

(4)

где I—наименьший момент инерции стеряг-ня, К—коэфф. устойчивости, зависящий от закона изменения 1(х) вдоль длины стержня и от способа закрепления концов его.

Во втором столбце табл. 1, то есть при 7г=0 (фигура 12, А), даны, по Диннику, коэфф. устойчивости К для стержней с обоими опертыми концами. Если 1{х) меняется вдоль длины стержня от середины к обоим концам по квадратному закону (параболоид вращения, клепаная пирамидальная стойка) и по закону 1-й степени (конус), то I обозначает наибольший момент инерции посредине стерягня, а г—наименьший у концов.

Таблица 1 .—К оэффициент устойчивости К.

		0	0,2	0,4	0,0	0,8
0,01		3,45	4,73	6,58	8,62	9,71
		2,55	3,65	5,42	7,99	9,63
		6,37	7,49	8,61 8,49	9,44	9,81
0,2		6,14	7,31		9,39 9.63	9,81
0,4		7,61	8,42	9,15		9,84
		7,52	8,30	9.10	9,62	9.84 9.85
0,6		8,51	9,04	9,48 9,46	9,74
		8,50	9,02		9,74	9,85
0,8		9,24	9,50	9,70	9.82	9.86
		9,23	9,50	9,69	9,81	9,86

Остальные столбцы табл. 1 дают К для случая фигура 12, В, когда средняя часть стержня длиною h имеет постоянное сечение, к обоим же концам сечения стержня суживаются. Если силы распределены вдоль длины стержня (фигура 13), то критич. значение такой нагрузки, то есть то ее значение, при к-ром начинается продольный изгиб,

г _ KEI

ъкр. 12 W

Для вертикального стержня постоянного сечения, к-рый искривляется от собственного _х веса, значения К для случаев закрепления концов, указанных на фигуре 10,11, А и 11, Б, соответственно равны: 7,87; 18,5 и 73,6.

Если, кроме собственного веса Q, на вертикальный стержень действует продольная сжимающая сила Р, приложенная на конце его (радиомачта с одной системой оттяжек на конце), то К для случаев закрепления концов, указанных на фигуре 10 и фигура 11, А, даны, по Н. Гришковой, в таблице 2 (т обо-Фигура 13. значает отношение собственного веса стерзкня <3 к эйлеровой критической силе для рассматриваемого случая).

Т а б л. 2.—К оэффициент устой чивостийГ.

Til.	0	0,25	0,50	0,75	1	2
К (фигура 10). ·	2,47	2,28	2,10	1,91	1,72	0,95
К (фигура 11, А).	9,87	8,64	7,40	6,17	4,93	0

Все приведенные результаты верны только в том случае, если напряжения не превосходят предела пропорциональности. Для каждого материала, при любом закреплении концов и любой форме стержня, можно установить ту длину, начиная с которой предыдущие выводы неприменимы. Так, длина Ϊ железного стержня постоянного сечения при обоих опертых концах должен быть больше 100 г, где г—наименьший радиус инерции стержня. Для более коротких стержней, зная зависимость между напряжением и деформацией за пределами упругости, можно тоже теоретически найти Р_кр. Но при расчетах проще пользоваться эмпирич. ф-лами. По Ясинскому, для железных стержней с обоими опертыми концами критич. напряжение Р_кр. — 13 380 — 14,83 к г/см² для * < 110.

По Тетмайеру, для чугуна при 1>80гможно брать формулу Эйлера, при меньшей же длине

Р_Кр. - [? 760 -1201 + 0,53 (у²] кг1см“;

для дерева при I < 110 г

Ρχρ.—[293 — 1,94 Л кг;см?.

Лит.: Я с и н с к и и Ф. С., Собрание сочинений, т. 1, СПБ, 1902; Т и м о ш е н к о С. И., Теория упругости, ч. 2, П., 1916 (указана лит.); е г о ж е, Курс сопротивления материалов, 8 издание, М.—Л., 1929; Д и н н и к А. И., О расчете стоек переменного сечения, «ВИ», 1929; Гришкова Н. II., Влияние собственного веса на продольный изгиб стержней, «ВИ», 1928, 3. А. Динник.