> Техника, страница 48 > Излучение

Излучение

Излучение, процесс выделения энергии, сопровождаемый распространением ее в пространстве в виде электромагнитных волн (смотрите Волны, Волны электромагнитные).

Свет молено рассматривать как лучистую энергию с длиной волны А в пределах 0,380ч-0,790 μ, воспринимаемую глазом. И. одной определенной длины волны называется м о-н о х р о м а т и ч е с к и м, или одноцвет-II ы м. Практически оттенки различных цветов объединяют в ограниченное количество групп, образующих основные цвета в пределах определен, интервалов длин волн (в μ):

Фиолетовый.. 0,380-1-0,430

СИНИЙ.. 0,430-1-0,485

Сине-зеленый.. 0,485-4-0,505

Зеленый.. 0,5054-0,585

Желтый.. 0,5854-0,605

Кр асный.. 0,6054-0,700

По отношению к световым явлениям различают два основных вида И.: калорическое, или тепловое, и люминесценцию (смотрите). Источником теплового И. является тепловая энергия лучеиспускающего тела, и этого вида процесс И. света всегда сопровождается повышением Т° светящегося тела. К этому виду И. относится наибольшее количество применяемых на практике источников света (смотрите Источники света).

Законы теплового И. Способность раскаленного тела излучать энергию при определенных длине волны и Т° находится в тесной зависимости от его поглощательной способности при тех же условиях. Эта зависимость выражается законом Кирхгофа:

	,	,	р(П)
Гя-	ел_	еЛ	еЛ
	<*Л	ал	~ а(п) ~ аЛ
здесь	еЛ >	ел,	β(η). ···> °л

= Const

=—1 •Aa=iJ.

(1)

-энергия, излучаемая различными телами с единицы поверхности в единицу времени, для длины волны А при температуре Т; αχ, α_λ, α"_λ, ., а— поглощательная способность этих же самых тел при тех же А и Т. Для непрозрачных тел а_д=1 — ρ_Λ, где ρ_λ—отражательная способность этого тела, Ε_λ—энергия, излучаемая телом, обладающим способностью полного поглощения энергии (Д;.= 1) и называемым абсолютно черным телом. Очевидно, что для всякого тела при темп-ре Т и длине волны А мы имеем: [е_д=«д · Ε_λ]_τ. Из этого ур-ия делается очевидной важность определения И. абсолютно черного тела при различных условиях, т. к., зная величину Е_{х т} и измерив для интересующего нас тела α_{λ т}, мысможем определить и е_хт. Числовые значения поглощательной способности а для различных тугоплавких металлов и графита при комнатной температуре приведены в таблице 1.

Таблица 1.— Значения поглощательной способности αχ.

Название
	0,4 μ	0,5 μ	0,6μ	0,7 μ
Платина. Иридий. Вольфрам. Тантал. Молибден. Железо. Никель. Графит.	0,51 0,40 0,53 0,56 0,50 0,47 0,79	0,415 0,353 0.51 0,62 0,55 0.45 0,39 0,78	0.358 0,331 0,49 0,55 0,52 0,42 0,35 0,77	0,31 0,32 0.46 0.45 0,50 0,41 0,31 0,76

При изменении темп-ры приведенные в таблице значения а_л должны изменяться; од

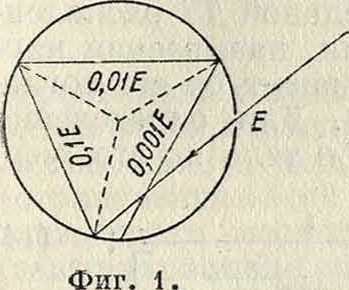
нако, для практических подсчетов вполне допустимо пользоваться данными таблицы в том виде, как они здесь приведены. С другой стороны, из приведенного выше основного ур-ия не трудно видеть, что абсолютно черное тело при всяких длинах волн и при всякой Т° обладает наибольшей из всех тел природы способностью излучать энергию. В виду отсутствия в природе тела с абсолютно черной поверхностью абсолютно черное тело осуществляется искусственно в виде особой конструкции полого шара или цилиндра с узким отверстием, изготовленного из огнеупорного материала с зачерненной внутренней поверхностью. Идей полного поглощения такого абсолютно черного тела легко понять из фигура 1. Если поглощательная способность внутренней поверхности его А_{λ т}=0,9, то после первого отражения тело отражает 10%, после второго—1 % и после третьего — 0,1%; если же после третьего отражения луч выйдет из отверстия, то поглощательная способность такого тела Α_{λ Τ}=0,999, то есть весьма близка к единице. При опытах с таким телом необходимо во всех точках полости поддерживать одинаковую температуру. При указанных выше условиях И. внутренней поверхности такого полого шара, наблюдаемое через малое отверстие, можно принять за И. абсолютно черного тела. О. Люммер при своих классических исследованиях температурного И. пользовался таким искусственным телом, выполненным в виде цилиндра с несколькими поперечными диафрагмами.

Фигура 2.

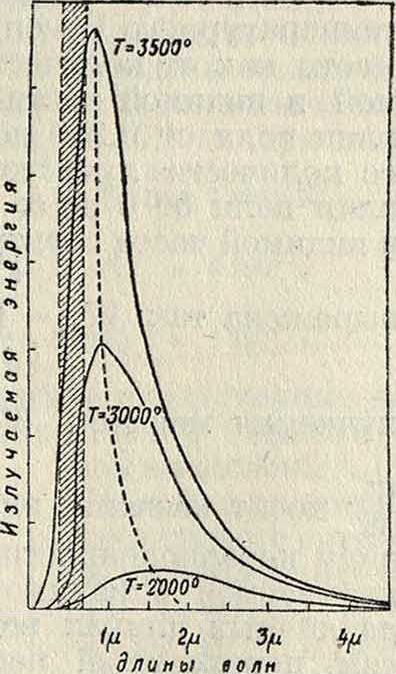
Излучение абсолютно черного тела. При накаливании твердых и жидких тел обыкновенно имеет место с и л о ш-и о и спектр И., характеризующийся плавной кривой распределения энергии в различных участках спектра. Раскаленные газы обыкновенно дают прерывистый, или линейчатый, спектр, и кривая распределения энергии не имеет непрерывного вида. Если по оси абсцисс отложить длины волн Я, а ио оси ординат—значения мощности монохроматич. И. для каждой длины волны Ε_λτ, то для абсолютно черного тела при различных темп-pax получим кривые, представленные на фигуре 2. Анали-тич. выражение для кривых распределения энергии абсолютно черного тела дает формула Планка (смотрите Вина-Планка закон излучения):

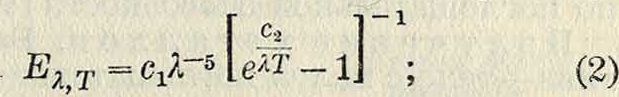
при выражении мощности И. Ε_λΤ в W с 1 c.w²,

длины волны Я в сантиметров и темп-ры Т, отсчитываемой от абсолютного нуля, постоянные ур-ия Планка будут:

с_г=2м²П ; с₂ =,

где с—скорость света; h=6,554 х 10~²⁷эрг/ск.; к=1,372 х 10~¹⁰ эрг/град. (h и к—универсальные мировые постоянные). Интегральное, или полное, И. абсолютно черного тела W во всех областях спектра, при длине волн от 0 до оо, подчиняется закону, выведенному экспериментально Стефаном и теоретически Больцманом:

W=] Ε_λάλ=σΤ“, (3)

О

где

α= 6,4941-=5,70 х 1(Г¹² W/c.*i²rpafl.⁴

Графически W на фигуре 2 метров б. выражено площадью приведенных кривых. Ф-ла Стефана-Больцмана м. б. получена путем замены Ε_λ ее значением из ур-ия Планка и последующим интегрированием. Дифференцируя формулу Планка, можно получить уравнение, выражающее зависимость между длиной волны λ,_ηαχ, при которой Ε_λ имеет максимум, и темп-рой Т (смотрите Вина закон смещения): Кюх Т=Const=2 940, (4)

Подстановкой в формулу Планка значения λ,_ηαχиз ур-ия Вина можно получить второе ур-ие Вина, устанавливающее связь между максимальным значением Ε_λ и темп-рой Т:

Ε,ηαχ Т~⁵=Const=2188. (5)

Абсолютно черное тело по сравнению с другими телами представляет собою излучатель с максимальной возможностью Й. для всякой длины волны при данной У°. По характеру распределения излучаемой энергии в различных частях спектра остальные тела природы м. б. разделены на два класса: тела с серым И. и тела с И. изб и р ательным, или селективным. И. серого тела, в смысле относительного распределения энергии в спектре, очень мало отличается от И. черного тела, уступая последнему в интенсивности. Поэтому все законы абсолютно черного тела применимы но отношению к И. серых тел; изменяются лишь константы и показатели степеней определяющих ур-ий. Избирательное И. имеет распределение энергии в спектре, отличающееся от такового у абсолютно черного тела и не подчиняющееся законам черного И. Обыкновенно тело с избирательным лучеиспусканием имеет относительный максимум И. в видимой части спектра при меньшем количестве энергии, излучаемой в других участках спектра. Поэтому избирательность И. является весьма желательной для получения источников света с большой экономичностью. Большинство металлов обладают серым И. Количество энергии, излучаемой серым телом, тем меньше, чем больше отличается данное тело от черного тела но поглощательной способности (табл. 1).

Излучение металлов. Белая платина—тело с малой поглощательной способностью; поэтому она представляет интерес как наиболее отличающийся от абсолютно черного тела излучатель. Уравнения И. платины таковы:

π_η=$Ε_λάλ=ο{Γ (С)

о где о₁=0,0001135 о из ур-ия (3);

Я-тах ‘ Τ= 2630; (7)

Е,шхТ-*=Const-3 476-10-«. (8)

При сравнении с абсолютно черным телом можно найти, что при красном калении платина не излучает и ¹/₁₀ количества энергии, излучаемой абсолютно черным телом при той же Т°. При высших Т° И. платины все же остается меньшим половины по сравнению с абсолютно черным телом. Остальные металлы занимают промежуточное полол-се-пие между платиной и абсолютно черным телом. Для И. чистых металлов имеют место ф-лы Ашкинази:

£l

Ε_λ/Γ=с_г · 0,0221 VojT Я"⁵·⁵ (е“т _ l)-i; (9)

W_M=Ε_λάλ=q · 4,936 · 10-²⁰ Vq~_uT°; (10)

и

λ_ηιαχ·τ= Const=₆^C;„; (11)

E_max Τ-*=_Cl · 1,334. ΙΟ-²³ УТ₀; (12)

здесь все обозначения аналогичны обозначениям формулы Планка (2); ρ₀—удельное сопротивление металла при 0°.

Излучение света абсолютно черным телом зависит от количества энергии, излучаемой в видимой части спектра в пределах длин волн от 0,380 до 0,790 μ. Необходимо, однако, заметить, что энергия, излучаемая при крайних значениях длин волн видимой части спектра, не дает большого светового эффекта вследствие того, что глаз неодинаково чувствителен к волнам различной длины. О кривой чувствительности глаза в различных частях спектра см. Видимость. Из приведенных выше кривых фигура 2 и ур-ий (3) и (4) можно видеть, что излучаемая энергия абсолютно черного тела при повышении темп-ры возрастает весьма быстро. Увеличение количества энергии, излучаемой в видимой части спектра,

в,

в“

создает вместе с повышением температуры повышение яркости абсолютно черного тела. Эмпирич. формула, выражающая зависимость между яркостями при двух смежных значениях Т°, будет й)· <«>

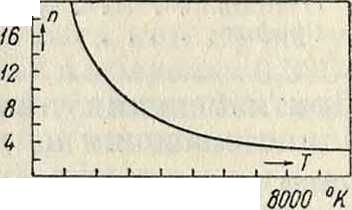
Значение п для абсолютно черного тела изменяется вместе с темп-рой Т по закону кривой, представленной на фигуре 3. При пользовании этой ф-лой для определения яркости интервалы Т° не должен быть большими во избежание понижения точности получаемых результатов. Яркость всякого раскаленного тела может служить _г0масштабом его Т°.

Ч е р н о и Т° какого-либо раскаленного тела называется Т°, которую имеет абсолютно черное тело при той же яркости, что и данное тело. Разница между черной и действительной Т° раскаленного «серого» излучателя, называемая иногда цветной Т°, зависит от его поглощательной способности. Для определения истинной Т° какого-либо тела по его «черной» Т° служит ур-ие:

2000 mo woo Фигура 3.

Т=-

iirm.

г

In

1 + а,(е

λΤ₄

-1)

(14)

здесь а_;—поглощательная способность данного тела (значения а_л для различных металлов приведены в таблице 1). Для У°ниже 3 000° подходит более простая ф-ла:

^1пал=т(т¹-Е^-) (¹⁵>

^{л л l} vein ¹ черн.

Здесь можно принять с₂=1,43 и А=0,65 μ, Световая отдача температурного излучения. Световая отдача всякого температурного И. определяется в зависимости как от количества энергии, излучаемой в видимой части спектра в пределах длин волн от 0,380 до 0,790 μ, так и от всего количества лучистой энергии в пределах длин волн от 0 до со. Энергия излучения В видимой части спектра аналитически м. б.

0,79

выражена так: W_e.=J Ε_λ·άλ, и полная из-

0,38

лучаемая энергия: W= jEyM. Отношение

О

носит название энергетического кпд. В

виду неравноценности для глаза энергии, излучаемой в видимой части спектра, при различных длинах волн, количество энергии, переходящей непосредственно в световое ощущение, можно получить, умножая элементарный поток лучистой энергии Ε_λ άλ при длине волны А на соответствующее значение числа колебаний ν_λ кривой видимости, при данной длине волны,взятой из этой кривой; тогда приведенное видимое И. выразится в виде

0.38

W_n.„.=ΐΕ_λ·άλ·ν_χ.

0,79

Отношение У"^с·· называется зрительным

W в. кпд видимого излучения. Отношена·,.,

ние носит название зрительного кпд полного излучения. Графически приведенные выше кпд молено выразить отношением соответствующих площадей,

о ψ 2/1 3JJ

Фигура 4.

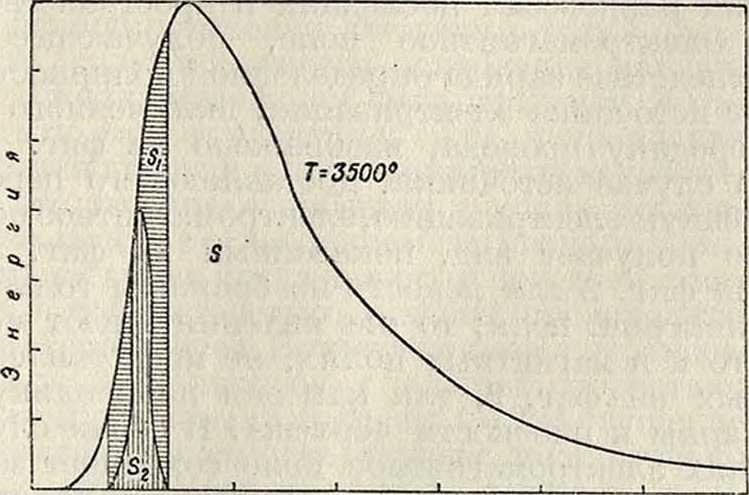
ограниченных кривой И. На фигуре 4 представлена кривая распределения энергии абсолютно черного тела при 3 500° К. Площадь (ограниченная всей кривой) S очевидно будет в известном масштабе равна W; площадь S_l(заштрихованная горизонтальными штрихами) будет равна W_e;, площадь S₂ (заштрихованная вертикальными штрихами)—W_n._e.

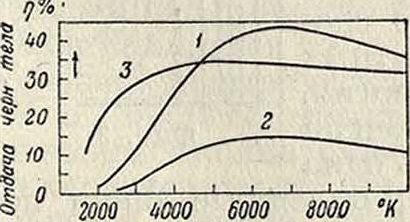
Тогда энергетич. кпд=зрительный кпд видимого И. —^ и зрительный кпд полного И.. Числовые значения для приведенных кпд зависят от Т°. Для абсолютно черного тела, по данным А. Р. Мейера, кривые изменения кпд в зависимости от Т° представлены на фигуре 5, где 1—· энергетич. кпд; 2—зрительный кпд полного И.; 3—кпд видимого И. (пределывидимого спектра 0,4-р0,7/<). Максимальные значения кпд и соответствующие им Т° следующие: w„

Максимум для=89,4% при " 000° К

W

» » —,^=14,5% » 6 500°»

W

» » - 89,8% » 4 250°»

Приведенные выше кривые и полученные из них максимальные значения и Т° максимумов вычислены А. Р. Мейером для пределов видимого спектра от 0,4 μ до 0,7 μ, при с₂=1,43; с_г==3,67· 10^-12 и о— =5,70 -КГ¹². Кри-

_{фиг 5} вая чувствительно сти глаза взята была по данным Айвса. При других положенных в основу данных результаты, естественно, будут отличаться от приведенных.

Световая экономичность абсолютно черного тела. Понятие световой экономичности, или световой отдачи источника света,определяется соотношением между излучаемой данным источником света световой энергией, выраженной в 1т или сферич. свечах, или свечах горизонтальных, и полной энергией, необходимой для получения данного светового потока, выраженной в W. Световая экономичность абсолютно черного тела как излучателя м. б. найдена путем измерения его яркости при данной Т° и определения из ур-ия (3) общей излучаемой мощности, приходящейся на единицу поверхности абсолютно черного тела при той же Т°. Отношение этих двух полученных величин будет характеризовать световую экономичность абсолютно черного тела. Данные для определения световой экономичности и значения световых отдач абсолютно черного тела приведены в таблице 2.

Таблица 2.—Световая экономичность и световая отдача абсолютно черного тела.

°к	Полное излуч. в W 1см“	Световой поток в 1т/слЦ	Световая экономичность
			абсолютно черное тело в lm/W	идеальный излучатель в lm/W
1500	28,9	2,28	0,0079	131,5
2 000	91,2	131,50	0,1445	171,8
2 500	222,6	1 550	6,96	198,0
3 000	462	7 950	17,60	211,0
3 500	855	27 500	32,20	218,5
4 000	1 459	70 000	48,00	221,2
5 000	3 563	251 500	70,50	219,5
6 000	7 390	591 500	80.00	211,5
7 000	13 690	1 090 000	80,10	201,2
8 000	23 350	1 758 000	75,40	198,0
9 000	37 400	2 580 000	69,00	191,0
10 000	57 000	3 560 000	62,40	188,0

При построении непрерывн. кривой световой экономичности абсолютно черного тела можно определить максимальное ее значение. Это значение будет равняться 81,5 lm/W. Если заменить абсолютно черное тело таким идеальным излучателем, к-рый имел бы такое же количество и распределение энергии, как и абсолютно черное тело, но вся энергия излучалась бы исключительно в пределах видимого спектра, то можно получить значения световой экономичности значительно бблыпие, которые и приведены в последней графе табл. 2. Идеальным случаем светоиз-лучения было бы превращение всей лучистой энергии в радиации монохроматич. света с длиной волны, соответствующей максимальной чувствительности глаза. Согласно кривой видимости максимальная чувствительность глаза имеет место при длине волны А s 0,556 μ. Соотношение менаду излучаемой мощностью в W и световым потоком монохроматического И. с длиной волны 0,556,« носит название механического эквивалента света; величина его равняется 0,0016 W на 1 lm. Соответствующее этому случаю светоизлучение на 1 W равняется 624 lrn.

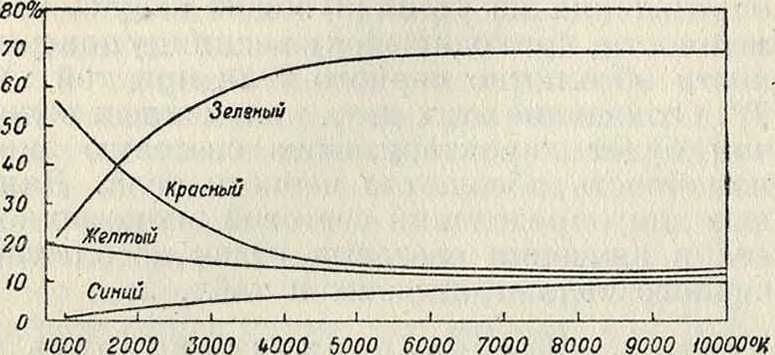
Из всего вышеизложенного следует, что основными условиями получения наибольшей экономичности источника света являются следующие: 1) по возможности вся подведенная "энергия должна превращаться в лучистую энергию; 2) И. энергии вне видимой части спектра должно быть наименьшим. В случае температурного И., как можно видеть из приведенного выше, представляется выгодным для этого повышать Т° светящегося тела. Цвет излучаемого света зависит от распределения энергии в пределах видимого спектра. При повышении Т°, как было указано ранее, максимум И. передвигается в область синих лучей. Распределение энер-

Фигура 6.

гии раскаленного абсолютно черного тела в различных областях спектра при различных Т° дает кривые фигура 6. И. света другими источниками, их рабочие темп-ры и кпд приведены в таблице 3.

Т а б л. 3 .—И злучение света, Г и кпд р а з-н ы х источников света.

	Дей-		Кпд
Название источника	ствит. теми-ра в СК	lm/W	энер- гетич.	зрительн. полного И.
Парафиновая и стеариновая свеча.	1 700	0.0936	0,063	0,017
Керосиновая лампа.	1 850	0,2S2	0,17	0,05
Керосинокалилытый свет.	1 850	1ЛЗ	0,70	0.20
окалильн. свет Газовая разрезная горелка.	1 750	0,565	0,37	0.10
	1 000	0,192	0.12	0,034
Газокалильный свет	2 000	1.13	0,65	0,20
Ацетиленов, горелка	2 400	0,631	0.33	0,11
Ацетиленокалильный свет.	2 400	2.26	1,20	0,40
Лампа с угольной цитыо 3,9 W/ropua. свечу.	2 135	2,94	1.80	0.52
i Лампа с танталовой дитыо 1,7 W/гориз. свечу.	2 200	5,65	3,10	1,00
j Лампа II ернста.	2 600	4,75	2.30	0,84
Вольфрам, иустотн. : лампа 1,2 W/гориз. свечу.	2 335	8,35	5,30	1,80
Вольфрам.лампага-! зополная.	2 745	18,90	9,20	3,40
, Дуговая лампа с чи-; ОТЫМИ углями.	4 200	7,10	3.20	1,30

Лит.: М а и з е л ь С. О., Оптика, II., 1923 (ли-тогр.); его те, Свет и зрение, Л., 1925; Meyer Λ. II., Wissenseliaftliclie Urundlagen d. Lichterzeugung, Liclittechnik, lirsg. v.L. Bloch, Mch.—B.,1921; L u m-mer O. Grundlagen, Ziele u. Grenzen d. Leucht-technik, Mch.—B., 1918; Plank M., Vorlesungen

liber d. Theorie d. Warmestralilung, 5 Aufl., Lpz., 1923; Henning F., Temperaturinessung, Brschw., 1915; Cady F. a. Dates H., Illuminating Engineering, i. 1925; Lorent! H. A., Theorie d. Slralilung, Lpz., 1927. А. Иванов.