> Техника, страница 48 > Излучение и прием электромагнитных волн

Излучение и прием электромагнитных волн

Излучение и прием электромагнитных волн —два основных процесса во всей радиотехнике. Так как фактически прием электромагнитных волн сводится также к излучению, то, естественно, ббльшее внимание уделяется в теории и практике вопросам именно излучения, процесса отправления электромагнитных волн в пространство, имеющего конечной целью передачу электромагнитной энергии без проводов.

Излучение. Физическое представление излучения электромагнитных волн f¹]. Необходимым условием для излучения электромагнитной энергии, то есть возникновения распространяющихся электромагнитных волн, является: 1) возможность вырабатывания запасов электрич. и магнитной энергии и 2) нарушение условий равновесия последних в пространстве.

Электромагнитное иоле, получающееся вследствие заряда определенной полярности от источника электризации, включенного в середину провода, изображено на фигуре 1. В случае источника, доставляющего переменную электризацию,электромагнитное поле получает вид, показанный на фигуре 2. На фигуре 2 для ясности изображены только электрич. поля; те же явления имеют место и в магнитных полях, не представленных на фигуре 2, так как они перпендикулярны к плоскости чертежа. В обоих случаях электромагнитное поле сохраняет зависимость от проводника, у поверхности

Фигура 1. Фигура 2.

которого положено начало его возникновению; электрич. силовые линии опираются своими концами на поверхность проводника; а т. к. величина электрич. силы у поверхности наибольшая, то электромагнитная волна в пространстве сохраняет связь с волной, распространяющейся по поверхности проводника.

Вследствие ограниченности размеров проводника волна, распространяющаяся по его поверхности, доходит до конца, за которым дальнейшее ее распространение невозможно: получается отражение волны, сопровождающееся интер-ференцией и образованием стоячих волн на поверхности проводника. В эти моменты в пространстве, окружающем часть проводника, на которой возникают стоячие волны, происходит образование свободных электромагнитных волн—излучение энергии.

Этот процесс изображен на фигуре з. фигура 3, где дана лишь одна половина вибратора; сплошные линии показывают направление электрич. сил, пунктирные—течение энергии (направление магнитных сил легко находится, например, по правилу трех пальцев, и т. д.).

Фигура 3, А соответствует моменту, когда волна только что достигает края проводника. Пренебрегая активным сопротивлением последнего, магнитную силу считаем во всех точках пространства в одной фазе с электр. силой у проводника. Энергия течет вдоль.

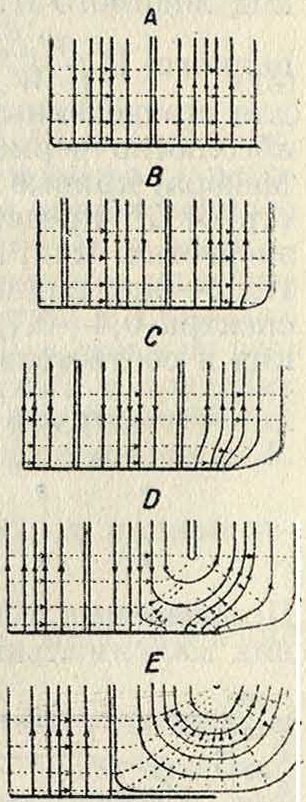
проводника от источника в пространство. Так как далее волна распространяться не может, то силовые линии, бегущие сзади, набегают на передние и тем вызывают сгущение поля у свободного конца проводника. Волна, распространяющаяся в свободном пространстве, ие встречая препятствий, продолжает перемещаться—линия электрическ. силы изгибается (фигура 3, В). Вследствие постепенной остановки движения линий элек-трич. силы получается ослабление магнитного поля; магнитная сила начинает отставать по фазе от электрич. силы; направление течения энергии в пространстве не меняется, но это течение ослабевает у конца проводника вместе с ослаблением магнитного поля. В то же время сгущение поля передается назад с той скоростью, с какой происходило движение вперед. Встречапрямой и отраженной волн происходит с двойной скоростью; поэтому в момент времени t=Т/4 сгущение достигает максимума, будучи локализовано посредине. Магнитное поле исчезает, т. к. сдвиг фаз достигает π/2; поэтому течение энергии прекращается (фигура 3, С).

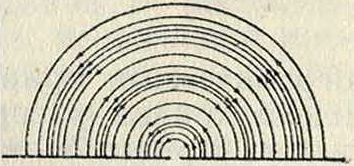
Вторая стадия начинается с движения силовых линий в обратном направлении. Сгущение поля исчезает; этому благоприятствует то, что встречная полуволна шлет поле обратного направления. Движение линий все ускоряется, усиливается магнитное поле; поток энергии вновь появляется, но уже с другой стороны; энергия расходуется отчасти на тепло Джоуля в проводнике (фигура 3, D). Стадия заканчивается тем, что вся отрицательная полуволна, идущая от источника, наложится на отраженную положит, полуволну, и к моменту t=T/2 электрич. поле у поверхности проводника совсем исчезнет. При этом процесс будет происходить уже по всей половине длины волны. Вся энергия, сосредоточенная в пространстве, заключается в кинетич. энергии магнитного поля; потенциальная энергия отсутствует, течение энергии приостанавливается. Эта стадия и сопровождается образованием свободных электромагнитных волн в окружающем пространстве—излучением. Действительно, одна за другой электрич. силовые линии, уничтожаясь у поверхности проводника, теряют, т. о., точку опоры. Остающиеся в пространстве их части, изгибаясь, замыкаются в кольца и как бы отрываются («отшнуровы-ваются») от остальной системы. К концу второй четверти периода у края проводника устанавливается стоячая полуволна: в прилежащем пространстве все остатки силовых линий сомкнутся кольцами, и образуется свободная электрическая волна (фигура 3, Е).

Т. о., процесс отражения электромагнитной волны отконца проводника представляет три характерные стадии, причем продолжительность каждой из них равна четверти периода колебания. Признаки первой стадии—расхождение фаз электрич. и магнитной силы; при этом на проводнике образуется стоячая волна, энергия которой запасена в потенциальном виде. Вторая стадия характеризуется возникновением свободной волны у поверхности проводника—в этот период энергия стоячей волны превращается в кинетическую форму. В третьей стадии свобод ная волна получает движение в пространстве. Затем повторяются лишь вторая и третья стадии, так как расхождение фаз, раз совершившееся, сохраняется все время одним и тем же. Следствием названных процессов оказывается непрерывное излучение в пространство. Т. о., электрический колебательный процесс всегда сопровождается образованием стоячей волны, то есть неравномерного распределения потенциала и тока; в одних системах проводников эта волна выражена яснее, в других—менее; поэтому каждая система имеет б. или м. значительную способность излучения волны в пространство. Математич. анализ возникновения электромагнитной волны дан впервые Герцом для случая нек-рого идеального вибратора, названного диполе м (смотрите диполь э л е к-трический), являющегося простейшим элементом, к которому («элементарному диполю») приводятся все остальные виды излучающих систем.

Поле вокруг передающей антенны. В своей работе о распространении электрических сил Герц определил силы электрич. и магнитного полей, которые появляются вокруг колеблющегося электрическ. диполя.

Электрический момент диполя определяется так: М —

= lq, где I — длина диполя, a q—переменный заряд его.

Для нахождения тока г, появляющегося в диполе, необходимо продифференцировать момент по времени:

<ш

dt

==и;

d‘M_ ,, di_

,ΙΓ- I ¹ dt

(1)

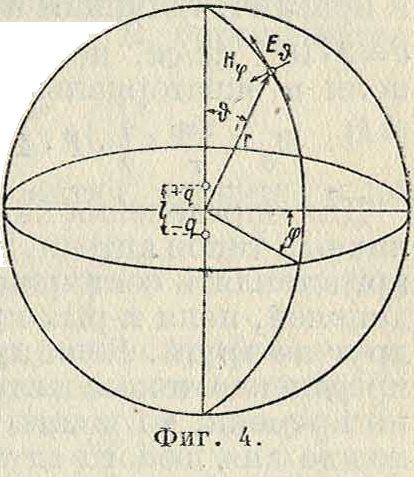
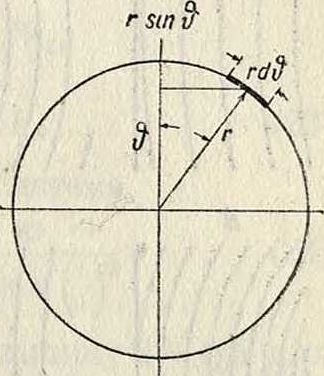
В полярных координатах (фигура 4) положение каждой точки определяется ее расстоянием г от центра, углом широты 8 и углом долготы φ. В этой системе координат силы электрич. и магнитного полей диполя выражаются так:

Я = <Р	sin# I /, Г 1 7· "Г	Г 1	S
		с
	sin # { сг/, Г ; г2 1	< ,г, г +1	г	> (2)
			~с
	2 <‘OS # с2/,	с.Г
	г г2	r~! t-r

Здесь в ф-иях /, и f" везде надо подставить аргумент t — т. к. имеем волны, двигающиеся из начальной точки со скоростью света е. Для малых расстояний (d=SA/2?i) главное значение будут иметь первые члены в скобках ур-ий (2), т. к. другие при этом исчезают. Здесь магнитное поле, по первому ур-ию (2), подчиняется точно закону Био-Савара, а электрическ. иоле—точно закону Кулона. Силы полей уменьшаются со второй и даже с третьей степенью расстояния, так что действие стационарных зарядов и токов на нек-ром расстоянии совсем исчезает. Для больших расстояний будут иметь значение одни последние члены скобок, так как радиальная составляющая силы поля Е_г исчезает почти совершенно по сравнению с тангенциальной Е₉. При синусоидальном изменении тока имеем:

J sin ωί (3)

и, по уравнению (1),

/"=ωΙΙ cos со (i — - (4)

Подставляя это значение f" в ур-ия (2), получим для больших расстояний силы поля:

^Е-ъ= ^οΗφ=-sin# cos со (ί-£). (5)

Силы электрич. поля (в меридиональных плоскостях) и магнитного (по кругу широты) увеличиваются от полюса к экватору пропорционально sin#. По оси полюсов они равны нулю, в плоскости же экватора принимают максимальное значение. Обе величины не зависят от угла <р, то есть поле направлено симметрично во все стороны. Переходя

2 лс к практич. единицам и подставляя ω=— и с=3-Ю¹⁰ см/ск, получаем амплитуду силы поля в экваториальной плоскости (в V/ж):

Ε^ψ· {·Ι·10-»=β0π· (6)

Для определения характера действия различных типов антенн, последние надо всегда представлять состоящими из ряда герцовых диполей, поля которых просто накладываются друг на друга. Если при этом известно распределение тока в антенне и его изменение по времени, то можно найти математич. решение для любого случая такого рода. Интерес представляет гл. обр. поле на большом расстоянии, то есть в отдаленной или волновой зоне — зоне dy hr. чистого излучения.

Для этого случая принимаем во внимание только последние члены уравнений (2). Для знаменателя в выражении силы поля достаточно точно можно считать, что все расстояния г пункта наблюдения от различных элементов сложной антенны равны и параллельны друг другу; тогда сила электрич. поля, создаваемая каждым элементом антенны, выразится уравнением:

sin i

-Гу	f
	.

Фигура 5.

<ш,=-

Для большого расстояния dl sin&=dy, где dy есть наблюдаемый с такого расстояния элемент антенны (по ее высоте), причем координата у (фигура 5) должна считаться перпендикулярной к расстоянию г. Далее, вместо времени запаздывания г/с, в расчет молено вводить среднее для всех элементов антенны время, в к-ром дблжно учесть разницу, равную х/с, для различных элементов, причем здесь х означает уже протяжение антенны в направлении расстояния г. Подставляя среднее значение расстояния г и общую силу поля в каком-нибудь отдаленном месте пространства:

⁰ с

Если только распределение тока в антенне, то есть зависимость его от ж и у, известно, то это интегрирование можно всегда произвести для любой функции тока. Наиболее простым решение будет для линейной вертикальной антенны и сродных ей форм с любым прост- _у |

ранственным токораспре- .-

делением, у которых боковые, горизонтальные или наклонные части малы по сравнению с длиной волны; т. о., предполагается, что антенны возбуждаются стоячими волнами.

В этом случае координата х для всех элементов приблизительно одинакова, так что нет необходимости вносить в запаздывание особой зависимости для различных частей антенны. Изменение по времени для всех элементов также одинаково и, следовательно,

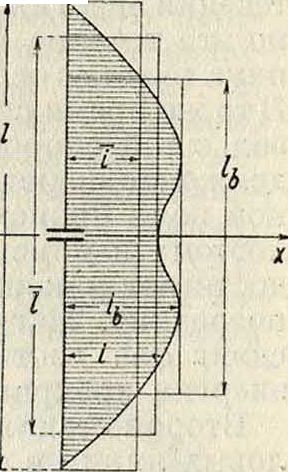
Фигура 6.

^{E =} y--TtS^idv

[ di l di

r₀ dt r₀ dt

(9)

при чем здесь l—средняя длина антенны,

г—ток в основании антенны, г—среднее значение тока, а I—длина всей антенны (фигура6). Из фигура 6 также видно, что можно обе эти

величины отнести к пучности тока и брать г_ь и 1_Ь. Это означает, что интеграл, входящий в выражение (9), представляет собою площадь тока антенны (как бы наблюдаемую с большого расстояния).

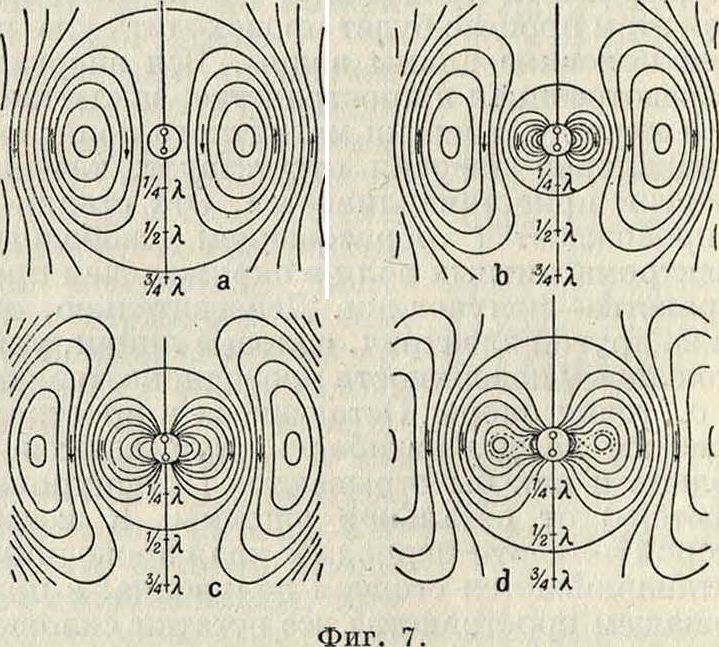
Значение поверхности земли. Для диполя, колеблющегося первой гармонической, Герц определил распределение электрич. силовых линий на среднем расстоянии от диполя в том виде, как они представлены на фигуре 7, a, b, с d. Фигура 7, а относится к моменту наибольшего тока в диполе, фигура 7, с—к моменту наибольшего напряжения на нем, две же остальные — к нек-рым промежуточным моментам. Согласно предыдущему объяснению, выходящие из диполя силовые линии распространяются в окружающее пространство и благодаря отталкиванию новым, противоположным по знаку, колебанием диполя не могут полностью вернуться в ηθχό; вследствие этого часть их отшнуровывается и распространяется в пространстве в виде свободного кольца замкнутых силовых линий. Распределение силовых линий на большом расстоянии от диполя см. Волны электромагнитные, где принята во внимание только верхняя полусфера, т. к. при расположении приемного диполя на земной поверхности распространение в нижней полусфере не представляет интереса. Такое разделение поля экваториальной плоскостью на две половины и будет иметь место при хорошей проводимости земной поверхности. Единственным необходимым условием для этого является перпендикулярность силовых линий к этой поверхности, что и выполняется. Отсюда вытекает, что любую вертикальную излучающую антенну можно заменить диполем, построив ее зеркальное изображение под землей, как это показано на фигуре 8. Поэтому для определения силы поля действующая длина I диполя должен быть заменена удвоенной действующей высотой антенны, т. e. l=2h.

В действительности земля проводит не бесконечно хорошо, что особенно заметно для станций, расположенных на суше. Благодаря этому у основания антенны, где токи проводимости переходят в землю, появляется значительное переходное сопротивление,условно обозначенное на фигуре 8 концентрацией земных токов у основания антенны. Это ‘/У?· сопротивление на больших установках может быть больше всех остальных сопротивлений, и поэтому всегда следует стремиться к его уменьшению; в практических радиостанциях располагают под антенной противовес (смотрите)—сетку из медных проводов, представляющую для тока незначительное сопротивление, или устраивают заземление (смотрите).

Мощность излучения. Электромагнитные волны, излученные колеблющимся диполем, несут с собой некоторое количество энергии, к-рое можно определить для любого направления фронта волны [см. Диполь электрически й, уравнения (13), (14) или (16)]. Для определения всей мощности W, излученной диполем, необходимо поток энергии через элемент шаровой поверхности dF (фигура 9) проинтегрировать по всей этой поверхности. Как видно из чертежа,

dF=г · d& 2лг sin &=2да·² sin # d&, (10)

а вся мощность, если подставить силу поля из выражения (5), выразится как

W=~ J* Я² dF=sin* 9 d& · (И)

О

Зная, что величина этого определенного ин-

Ό

I

Фигура 8.

теграла равна ⁴/₃, и принимая во внимание ур-ие (1), получим выражение для излученной диполем мощности в виде 2 Г>

w =

о а)·!*

W=~ I² cos² ωί.

Для периодического синусоидального тока, по уравнению (4), эта мощность выра-жается следующим уравнением:

(13)

Та же мощность должна все время подводиться от источника тока к диполю, конечно, если только интенсивность его колебаний все время постоянна. Так как мощность при периодических колебаниях пропорциональна квадрату мгновенного значения тока, то, следовательно, излучающий диполь является относительно источника тока сопротивлением, значение которого R_s определяется из выражения (13):

2 а>4*

Фигура 9.

3

² 8 я² ( 1 2

-ir^cUl·

(14)

или, по переводе в практич. единицы и по подстановке с=3-10¹⁰:

Д,- 8<b²(i)²· (15)

Это сопротивление излучения прибавляется к прочим сопротивлениям антенного устройства, но является полезным сопротивлением передающей антенны,которым учитывается эффект излучения электромагнита. поля. Для полусферы, то есть пространства только над поверхностью земли, и мощность и сопротивление излучения R_sбудут в 2 раза меньше, чем для всей сферы:

R_s={Rs· (16)

Если еще ввести эквивалентную высоту антенны согласно выражению l=2h, то сопротивление излучения для полусферы выразится уравнением:

R_s=160 π* 0)²· (17)

При неравномерном распределении тока и для определения излученной энергии также нужно вводить в формулы среднее значение силы тока или же действующую длину диполя или высоту антенны. Величины сопротивления излучения для обертонов антенны, определяемые только точной интеграцией, см. Короткие волны.

Прием. Физическое представление приема электромагнитных вол н. Когда электромагнитная волна, распространяясь в пространстве, встречает на своем пути проводник, она претерпевает изменение: часть волны отражается, часть по- глощается проводником. Каждая электрич силовая линия, дошедшая до проводника и поглощенная им, передает последнему свою энергию и вызывает в проводнике электрич. ток. Рассматриваем для ясности приемный диполь, центр которого находится в экваториальной плоскости излучающего диполя,

рл

Т. Э. m. VIII.

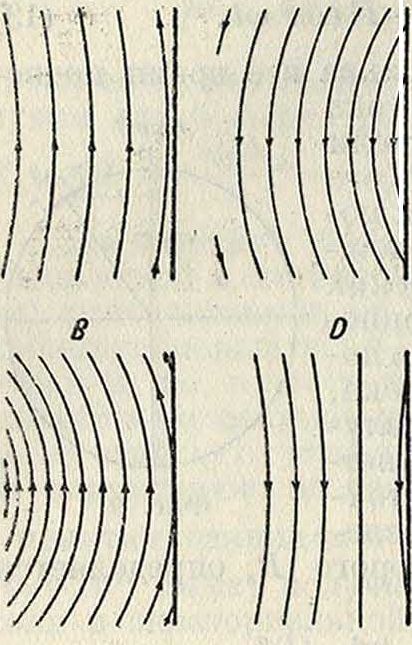
и считаем, что электросиловые линии замкнуты и первыми до поверхности проводника доходят передние части их; а т. к. эти части, войдя в проводник, уничтожаются, то вместо замкнутых силовых линий получаются разомкнутые, опирающиеся своими концами на проводник. Это вызывает появление на поверхности проводника зарядов; при обозначении,данном на фигуре 10, А, на верхней половине проводника образуется положительный заряд, так как там силовая линия начинается; на нижней половине — отрицательный заряд, т.к. здесь силовая линия кончается. По мере продвижения волны заряды обеих половин провода увеличиваются, так как число разорвавшихся элект-рич. линий увеличивается (фигура 10, В). По истечении нек-рого промежутка времени через проводник будет проходить центральная часть полуволны; в это время заряд проводника достигнет максимума, после чего заряд начинает уменьшаться, так как число разорвавшихся силовых линий уменьшается (фигура 10, С, D). За первой полуволной последует вторая, которая произведет такое же действие, но заряд верхней половины проводника будет уже отрицательным, а нижней половины—положительным; за второй полуволной последует третья и т. д.: проводник под влиянием электромагнитных волн приходит в колебательное состояние с периодом, соответствующим периоду приходящих волн; эти колебания будут вынужденными колебаниями. Однако, в тот момент, когда элек-трич.-силовая линия разрывается, оставшаяся часть оказывается наклоненной к поверхности проводника под весьма острым углом. Это не соответствует электрическ. равновесию, и силовые линии начнут скользить по проводнику, стремясь принять направление, перпендикулярное к его поверхности. Такое скольжение принимает колебательн. характер, т. к. проводник имеет изолированные концы, которые вызывают отражение. Действительно, электрич. заряды, представляющие собой концы силовых линий, дойдя до изолированного конца проводника, не могут далее двигаться в том же направлении, а вынуждены распространяться в обратном направлении; дойдя до противоположного изолированного конца, они испытывают снова отражение, и т. д. Вследствие интерференции, или наложения, прямых и отраженных волн в проводнике стремится установиться стоячая полуволна, соответствующая собственному колебанию проводника. Из предыдущего известно, что появление стоячей полуволны связано с излучением энергии в пространство. Т. о., проводник, принимаю щий волны, является одновременно и системой, излучающей их. Итак, в приемном проводе под влиянием воспринимаемых волн возникает два рода колебаний: одни—вынужденные, с периодом, равным периоду воспринимаемых волн, другие — собственные, с периодом, равным периоду данного проводника. При резонансе (смотрите) воспринимаемых волн и приемной системы возникновение этих колебаний происходит наиболее интенсивно.

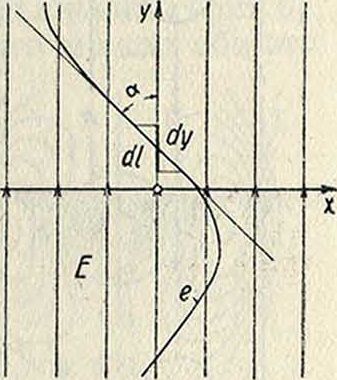
Напряжение в приемной а нте н-н е. Вдали от передатчика, в волновойзопе (смотрите) приема электрич. волн, сила электрич. поля направлена перпендикулярно к поверхности земли, сила же магнитного поля—параллельна последней. Кроме того, в земле параллельно ее поверхности существуют токи как следствие выравнивания потенциалов в проводящих слоях почвы. Все три поля м. б. применены для приема. Электрическ. поле можно уловить (воспринять из пространства) с помощью открытых антенн и, далее, использовать его с помощью приемника. Магнитное поле проявляется благодаря индукционному действию, оказываемому им на рамку или замкнутую антенну, и наконец, земные токи воспринимаются с помо-, щыо горизонтальных земных антенн, представляющих собою провода, расположенные в земле или по ней, по направлению приходящих волн. Ясно, что всегда желательно получить в приемном контуре возможно большую эдс, которая должна далее действовать на детектор. А так как и магнитные и электрич. силы, а также и поле земных токов неразрывно связаны между собой, то всегда бывает достаточно принимать в рассмотрение, например, только одну электрич. силу, действующую на приемный провод. В этом случае в каждом элементе провода dl, составляющем некоторый угол а с направлением электрического поля приходящей волны (фигура 11), действует переменная электродвижущая сила, равная E dl cos а. Вся электродвижущая сила, вызванная полем волны в приемном проводе, определяется из уравнения;

e=J E dl cos а, (18)

при чем интеграл берется по всему протяже-нию проводов. Если антенна имеет значительные размеры вдоль направления движения волны, то сила поля не во всех ее точках будет в одинаковой фазе. Под Е здесь приходится понимать значение силы поля, учитывающее запаздывание и равное Ε,χ, от-

⁰ С

несенное к нек-рому среднему месту антенны, воспринимающему волны в момент време-ни t₀. Соединим два остальных множителя в выражении (18) вместе и обозначим их через dy; тогда эдс, индуктируемая в антенне, определится по ф-ле:

e~jE .dy. (19)

t„-_c

А С

Фигура 10.

Фигура 11.

Очевидна аналогия этой ф-лы приема волн с выражением (8) напряженности поля, излученного передающей антенной. Простейшим оказывается расчет индуктированной эдс для вертикальн. открытых антенн, так как их направление точно совпадает с направлением электрических силовых линий. Сила поля для таких антенн будет в одинаковой фазе вдоль всего провода, и в выражении (19) ее можно вынести за знак интеграла. Тогда эдс, индуктируемая в такой антенне, .в свободном пространстве выразится так: е — Е1, или, если антенну рассматривать как открытую только над поверхностью земли, e=Eh. Если волны падают на антенну сверху (под острым углом), так что вектор силы поля образует угол а или направление движения волн—угол & с направлением антенны, то в эти ф-лы войдут еще множителями cos а или sin #.

Для форм замкнутых антенн (смотрите), для которых эдс е=— E cos φ,

при передаче, как и при приеме, обнаруживается сильное направленное действие, зависящее от угла ψ, образованного плоскостью рамки с направлением движения волны. В то время как в горизонтальной плоскости рамка обнаруживает ярко выраженное направлен. действие, волны, падающие сверху, воспринимаются ей неослабленными, так как в этом случае будут активными и вертикальные и горизонтальные части рамки. В противоположность открытой антенне, принимающей сверху приходящие волны весьма слабо, то есть имеющей направленное действие в вертикальной плоскости, а в горизонтальной плоскости принимающей равномерно, рамка имеет горизонтальное направленное действие и принимает равномерно вертикально приходящие поля.

Баланс энергии в приемной антенне. Антенна воспринимает из приходящего поля иек-рую энергию, определяемую (при резонансе) произведением напряжения е и силы тока в антенне I, причем последний может быть нами рассчитан. Среднее значение воспринятой энергии, в случае а ту соидальных колебаний,

W_e=el. (20)

Эта энергия и возбуждает колебания в приемнике. В сопротивлениях приемника теряется мощность, которая выражается по закону Джоуля:

W_r=i BP. (21)

Она служит в первую очередь для получения полезного действия, и, кроме того, часть ее теряется на нагревание проводов. R является, т. о., общим полезным и вредным сопротивлением, вносимым приемником. Так как приходящие волны вызывают в приемной антенне высокочастотный ток, последний вызовет, с своей стороны, излучение в пространство, окружающее приемную антенну. Поле же излучения каждой антенны по уравнению (2) определяется только током в эквивалентном диполе и не зависит от того, каким образом ток получен. В антенне передатчика он образуется благодаря внешней эдс, приложенной к передающему устройству, в приемной же антенне он вызывается приходящими волнами. Работающая приемная антенна, т. о., излучает вокруг себя энергию, величина которой рассчитывается по ур-ию (13). Тогда энергия, излученная приемником по всем направлениям, выразится следующим образом:

W_s=lR_sP. (22)

Закон сохранения энергии дает: W_e=W_r+W_s,

откуда

e=(B + R_t)l,

и сила тока в приемной системе

Е1

I =

R+R_s

R + 80 м

1 2

(23)

(24)

Здесь надо подставить величину I=е/Е для эдс, а для сопротивления излучения—I из выражения (15). Т. о., сила тока в приемнике зависит в одинаковой степени как от эдс, индуктированной приходящим полем в антенне, так и от суммы сопротивлений—активного и излучения. Первое из них задается полезным сопротивлением, причем значение сопротивления, вносимого им в антенну, молено менять путем изменения связи с приемником. Сопротивление же излучения задается размерами антенны и зависит только от действующей длины эквивалентного диполя и длины излученной волны. Если активное сопротивление R уменьшать так, чтобы оно стремилось к нулю, то, по выражению (24), ток I не делается бесконечно большим, а стремится к некоторому конечному пределу:

I =

1 А²

Е.

(25)

Это объясняется ослабляющим действием обратного излучения.

Эта предельная сила тока при заданной напряженности поля Е растет с квадратом взятой длины волны и уменьшается с высотой антенны или длиной диполя I. Такое парадоксальное явление особенно ясно наблюдается при короткой волне и большой высоте антенны, когда сильно увеличившееся действие обратного излучения значительно уменьшает силу приемного тока; таким обр., наилучшее приемное действие не соответствует наивысшей антенне. Действительно, изменение силы тока в зависимости от длины диполя, по (24), представляется кривой (фигура 12). Итак, при малых длинах R_a не велико, и сила тока растет с увеличением высоты антенны, т. к. преобладает влияние увеличивающейся эдс, воспринятой системой. При бблылих длинах диполя ток начинает спадать, т. к. возрастающее обратное излучение все более и более уменьшает его. Точка максимума тока имеет место при такой длине антенны, для

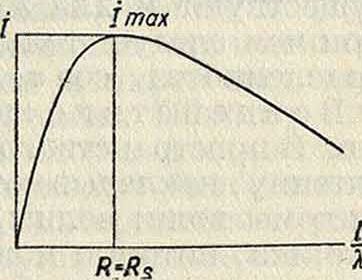
Фигура 12.

к-p ой сопротивление излучения равно полезному сопротивлению:

R_s=80π² (If)²=R. (26)

Отсюда вытекает, что наивыгоднойшая длина для диполя:

i ——ί /~E — E^^R. (27)

‘opt 2л У 21) 28,2

При этом ток имеет половинное значение против величины, вычисленной по уравнению (25). Подставляя силу тока из (24) в уравнения (20) и (21), получим величины действующих в приемной системе энергий. Мощность, воспринятая из приходящего поля, выразится уравнением:

w,=;

(28)

2 R + R_s’ мощность, теряемая в сопротивлении:

С29)

и, обратно, излученная или рассеянная мощность:

W. =

(30)

(К + R$)

Из всей мощности, теряемой в сопроти-влении W_r, конечно, только часть преобразуется в полезную, например акустич., энергию или для воздействия на реле быстродействующих аппаратов. Величина же этой мощности W,., как видно из (29), вдвойне зависит от сопротивления R. Она изменяется по такой ищ кривой, как на фигуре 12. Таким образом, закон оптимальности (26) применим не только для нахождения наивыгоднейшей высоты антенны при определенном сопротивлении, но и для установки наивыгоднейшего сопротивления при заданной высоте антенны. Полезная мощность в оптимальном случае, то есть при R=R_S, по выражениям (14) или (15), равняется _{w =}« Rs _ <.т

V fit·

(2 H_s)^s

8 Rs

_3 E4 ЕЧ‘

64 л^ас 640л³ ‘ О⁵¹)

Здесь предпоследнее значение выражено в абсолютных, а последнее—в практич. единицах. В этом случае, по выражению (30), рассеянная энергия W_s= W_r, а приходящая энергия при этом W_e=2tT_r. Все зависимости были выведены только для открытых антенн; легко показать, что они же существуют и для замкнутых форм сетей, причем следует только учесть фактор направленности, cos а.

Воздействие на первичное п о-л е. В пространстве, окружающем приемную антенну, накладываются друг на друга две системы волн: волны, приходящие от передатчика, которые можно считать плоскими, если приемник на большом расстоянии, и сферич. волны, излученные самой приемной антенной. Сила поля последних Е₂ на небольшом расстоянии г₂ от приемника рассчитывается по тому же ур-ию (6), выведенному нами для передатчика, только в него придется подставлять силу приемного тока 1₂

«*к“·

(32)

Приемный ток, по уравнению (24), определится формулой:

(33)

Сопоставляя эти ф-лы, получим отношение силы вторичного поля к силе первичного:

Е* ₌ ^60π _. IL. mi

Наибольшим вторичное поле будет для предельного случая R=0, при к-ром приемная антенна только рассеивает пришедшую к ней энергию. Тогда, по выражению (15),

у- · (35)

e_l

eV

3

4π

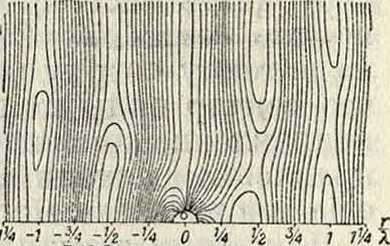
Фигура 13.

В этом случае на расстоянии длины волны от приемника вторичное поле равняется 24% первичного, на расстоянии же 24 длин волны оно составит только ок. 1%. Для оптимального случая (26) воздействие на первичное поле в два раза слабее, и уже на расстоянии 12 длин волны вторичное поле составляет 1% первичного. На фигуре 13 представлено для последы, случая распределение электрич. силовых линий в меридиональной плоскости, а на фигуре 14— распределение магнитных силовых линий в экваториальной плоскости. Внутри зоны воздействия принимаемые и излучаемые волны интерферируют между собой. Вследствие этого перед приемником образуется концентрация поля, за ним же создается теневое действие. Благодаря действию такой интерференции волн внутри зоны воздействия и происходит перенос энергии из пространствав приемную антенну.

Вычислим полезную мощность, захвачен. приемником, по формуле потока энергии, пересекающего определенную площадку в чистом поле излучения. Через каждый сл{² поверхности приходящей волны при синусоидальном изменении силы поля в единицу времени протекает поток энергии

Фигура 14.

S^^-EK 8 пс

(36)

Максимальная захваченная энергия, с другой стороны, выражается в абсолютных единицах ур-ием (31), и тогда величина поверхности, через к-рую она втекает в первоначальное поле излучения, выразится следующим образом:

771 _ ^^ГП!ПС· _ ?2

""" S 8д ·

(37)

Максимальный кпд электромагнитной передачи от излучающей антенны к приемной выражается так:

(^λγ.

¹ Wi 64π³ rj

Так, при Я=500 метров и расстоянии г=50 км, η=1,4· 10^-6, то есть из каждого kW излученной энергии в лучшем случае до приемника доходит 1 mW. Только применением передатчика с сильно направленным излучением и соответственно направленных приемных устройств можно улучшить кпд передачи электромагнитных волн.

Лит.: ¹) Петровский А. А., Научные основания беспроволочной телеграфии, ч. 1, СПБ, 1913.— Abraham М., Theorie d. Elektrizitat, 7 Auflage, В. 1, Lpz., 1923; Fleming J. A., The Principles of Wireless Telegraphy a. Telephony, 2 ed., L., 1910; Nesper E., Handbuch d. drahllosen Telegraphie, B., 1923; Zenneck J.u. Rukop IT., Lehrbuch d. drahtlosen Telegraphie, 5 Aufl., Stg., 1925; Ollendorff F., Die Grundlagen d. Ilochfrequenztechnik, B., 1926; Rfldenberg R., Aussendung und Erap-fang von elektrischen Wellen, B., 1926; Pierce Cl. W., Electric Oscillation and Electric Waves, L., 1920. В. Баженов.