> Техника, страница 49 > Индуктивное сопротивление

Индуктивное сопротивление

Индуктивное сопротивление, сопротивление, к-рое получается у движущегося в жидкости тела при наличии циркуляции, обусловливающей по теореме Жуковского нек-рую подъемную силу от определенной системы вихрей, образовавшихся в жидкости при движении данного тела (смотрите Вихревая теория). Эти вихри образуются следующим образом.

Предположим, что нек-рое крылообразное тело движется в воздухе; у него сила сопротивления получается как за счет трения, так и за счет придания некоторой массе воздуха определенных скоростей. При наличии у этого крыла подъемной силы, то есть силы, перпендикулярной к направлению движения потока, струя над крылом сужается, а под крылом расширяется, за счет чего соответственно получаются большие и меньшие скорости разных направлений; от этого по всему размаху крыла образуются вихри, составляющие общую вихревую пелену (фигура1), к-рая, сходя с крыла, практически, вследствие вязкости воздуха, понемногу размывается.

В теории И. с. пользуются методом, часто применяемым в гидродинамике: предполагается, что крыло создало определенную систему вихрей и эти вихри вызывают определенное поле скоростей. Чтобы охватить математич. анализом действие вихрей на окружающую их жидкость, предполагается, что с задней кромки крыла сбегает множество элементарных вихрей с циркуляцией J, причем, т. к., с точки зрения гидродинамики, всякий вихрь не может кончиться внезапно, то, в согласии с теорией подъемной силы крыла аэроплана, предполагается, что сбегающие с крыла вихри идут внутри крыла в виде нек-рых фиктивных," т. н. присоединенных вихрей с циркуляцией в каком-либо сечении крыла плоскостью, перпендикулярной размаху, равной сумме циркуляций элементарных вихрей, проходящих по одну сторону этой плоскости.

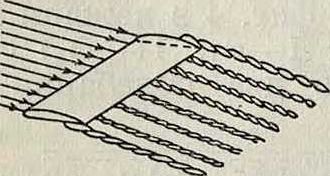
Фигура 1.

Согласно вихревой теории, вихри вызывают в потоке некоторую добавочную скорость; последняя, слагаясь с относительной скоростью движения крыла, дает ту истинную скорость, с которой воздух подходит и отходит от крыла. В общем случае эта вызванная скорость не постоянна по размаху крыла, а будет зависеть от интенсивности расположения элементарных вихрей, составляющих сходящую с крыла вихревую пелену. В частном случае система вихрей будет состоять из концевых и присоединенных прямолинейных вихрей—это т. н. П-образ-ные вихри. В некоторых случаях практики для упрощения расчетов м. б. принята приближенно эта схема распределения вихрей.

Зная вызванные определенной системой вихрей скорости и составляя уравнение связи крыла с потоком, то есть связь между ги-дродинамич. величинами, характеризующими поток, и величинами, характеризующими крыло данной формы, можно найти и необходимые характеристики каких угодно крыльев. Теория И. с. играет чрезвычайно большую роль в практике аэродинамич. расчета самолетов (смотрите Аэродинамика, расчет самолета), т. к. она позволяет по продувкам индивидуальных крыльев находить характеристики любых сложных крыльев. Так, по характеристике моно-планных крыльев различных профилей можно найти характеристики сложных крыльев, скомбинированных из этих профилей и как угодно расположенных в крыле; такими крыльями будут конические крылья, крылья с различными установками профилей, т. н. скрученные крылья, бипланы, тендемы и т. д.

Рассмотрим влияние прямолинейного бесконечного шнура с циркуляцией J (фигура 2) на какую-либо точку жидкости А и определим вызванную этим шнуром скорость в этой точке. Согласно сказанному в статье «Вихревая теория» (ТЭ,т. 3, ст. 776), бесконечно малый элемент шнура ds вызовет в точке А элементарную скорость

dv=sin ψ ds. (1)

4 яг^{2 Ύ 47}

А

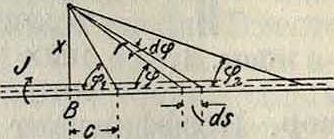
Фигура 2.

Так как г=—— и ds=-

Sin <р sin φ

Sill² φ

вызванная элементарная скорость dv=_T^J— · sin φ άφ.

4πχ ^{r τ}

d<p_t то

Интегрируя в пределах углов от φ₂ до φ_ΐ9получим полную скорость точки А от действия части вихря, заключенного между этими углами:

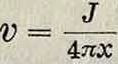
<Р 1

J sin φ άψ =

<Pi

J

4лх

(cos φ₂ — COS <Px).

(2)

В случае бесконечного шнура 9?₂=0, ψι=η₉и скорость

V =

J

2лх

(3)

В случае полушнура, то есть шнура, только одним концом простирающегося в бесконеч-

ность, а другим лежащего на перпендикуляре АВ, <р₂=0, 9г=-₂ и скорость

V=· (4)

4лх ^v

Рассмотрим скорость, вызванную вокруг крыла вихревой пеленой. Для этого будем полагать, что эта вихревая пелена аналогична бесконечному ряду П-образных вихрей (фигура 3). Возьмем какое-либо сечение крыла плоскостью, перпендикулярной к раз-

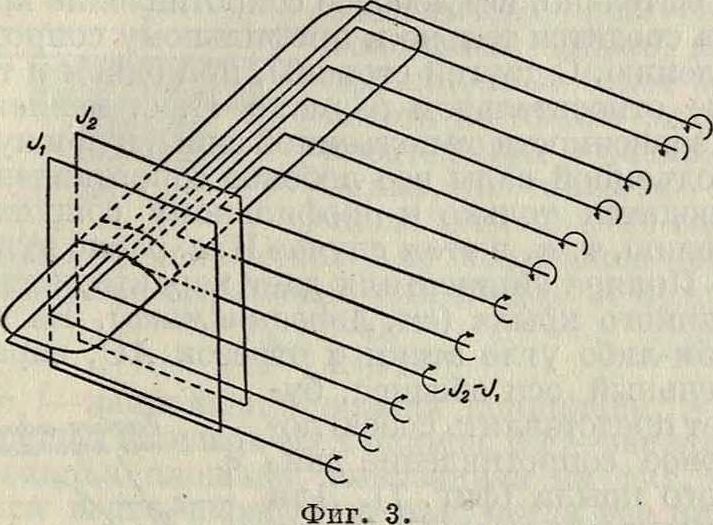
в маху и направленной по потоку, а также второе сечение, бесконечно близкое к первому. Обозначим циркуляции по контуру, охватывающему крыло и находящемуся в проведенной плоскости, соответственно через Jj и J₂. Выберем прямоугольную систему координат т. о., чтобы ось×шла по размаху крыла, ось Y—по направлению дви-z жения крыла и ось Z—

перпендикулярнопервым двум. Пусть на фигуре 4 Vs кривая ВСХ представляет собою закон распределения циркуляции по Сй, размаху. Обозначим абсциссы положения вихрей через х, а абсциссы точек крыла—через ξ. По формуле (4), скорость, вызванная элементом вихря с абсциссой х в точке А с абсциссой {, будет:

dx

Ϊ ’

Интегрируя это выражение по всему крылу, то есть в пределах от — 1до + ~, получим скорость, вызванную рассмотренной системой вихрей в точке А:

с	J
	А
	-Х-*
Фиг	4.

J 1 dj

dv=- -

4л dx×-

dJ 4л J dx l

dx

x - ξ

(5)

Рассмотрим теперь действие на поток вокруг крыла одного П-образн. вихря (фигура 5). По формуле (4) можно найти скорость, вызванную одним полушнуром:

4 лх

Эта скорость по размаху будет меняться по гиперболич.закону. Найдем среднюю по размаху величину этой вызванной скорости и назовем ее v_cp_ Т. к. концевые вихри, как показывает опыт, идут на нек-ром расстоянии от конца крыла, то обозначим раз мах крыла через I, расстояние между центрами вихрей—через ί_χ и расстояние от центра вихря до конца крыла — через е; тогда

h-i

^е=—’

Величина средней скорости

. 1+6 _т 1+6 j

4 л1

In

l -f- e

?

Так как в нашей системе имеются два вихря, то вызванная каждым вихрем средняя скорость удваивается, и средняя скорость, вы- -званная двумя концевыми вихрями в точке А, лежащей на присоединенном вихре, выразится так:

«V=2^Г^1п

г + е г

-I,

ж

ФПГ. 5.

Приближенно, на основании опыта, можно принять, что 1₁=ί·1,05; тогда h + i

In

h-ι

s4,

и, следовательно, средняя скорость

2 J

(6)

Чтобы найти ур-ие связи крыла с ^потоком, воспользуемся теоремой Η. Е. Жуковского (смотрите Аэродинамика, т. 1, ст. 835), по которой подъемная сила через циркуляцию выражается след, обр.:

Р=ρ J V I. С"

С другой стороны, эту подъемную силу можно выразить также следующей ф-лой (смотрите Аэродинамика, т. 1, ст. 841, формула 6):

Р=о Су- S - V².

Сравнивая эти две ф-лы, получаем:

(8)

s-v

= С„ · Ь · F;

подставляя же это выражение для J в ф-лу

(6) и вводя обозначение Я=1, к-рое называется относительным размахом или удлинением крыла, найдем:

Vcv.=k-^Cv-^b-V=h-C_y-V. (9)

Наличие этой скорости, вызванной вихрями, обусловливает собой отклонение относительной скорости потока у крыла на определенный угол Δα =. Этот угол называет ся скосом потока. Вследствие наличия скоса потока крыло в действительности встречает поток не под углом атаки а, а под углом α —Δα (фигура 6).

Подъемная сила крыла, движущегося со скоростью V, перпендикулярна скорости движения крыла. Это—та подъемная сила, с которой обыкновенно оперируют и к-рую находят при аэродинамич. испытаниях крыльев. Вследствие того, что направление потока скошено на угол Δα, подъемная сила также откинута назад на угол Δα. Если спроектировать ее на направление движения крыла, то получится некоторая сила Q_itнаправленная по скорости движения, то есть некоторая сила лобового сопротивления, вызванная строением самого потока около

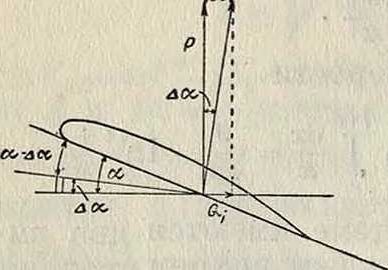
крыла и называемая индуктивным сопротивлением. Но при движении крыла от трения поверхности крыла о воздух и от различных побочных вихреобразо-ваний создается еще сила лобового сопротивления, зависящая исключительно от индивидуальных особенностей профиля крыла. Это сопроти-^фиг· ⁶ вление называется профильным сопротивлением; обозначим его через Q_p. Индуктивное и профильное сопротивления создают то лобовое сопротивление, которое и наблюдается при испытаниях крыла. Т. о., полное лобовое сопротивление

Q=Qi +. Qp

Т. к. скос потока является величиной сравнительно небольшой и проекция подъемной силы на новое направление изменит ее очень мало, то приближенно принимают, что подъемная сила за счет скоса потока изменяется незначительно; большое же изменение ее происходит за счет изменения угла атаки.

Согласно фигура 6, И. с. выражается следующим образом:

Qt= Р Аа,

а полное лобовое сопротивление Q=Р · Аа + Qp.

Подставив в эту формулу выражения сопротивлений через коэфф-ты сопротивлений, будем иметь:

C_x-Q-S-V*=C_v-e-S-V*- a + C_p-e-S-V где С_р можно назвать коэфф-том профильного сопротивления. Деля все выражение на в S V², получим:

С_х=С_у- Аа+С„, (10)

или С_х=С.1+С_р, где С_{—коэфф-т индуктивного сопротивления, выражающийся следующим образом:

С^Су-Аа. (И)

Коэфф. профильного сопротивления, как зависящий от индивидуальных особенностей профиля, не м. б. найден теоретич. путем; коэфф-т же И. с. зависит от угла скоса:

Αα=?ψ

Подставляя сюда найденное значение для средней вызванной скорости, получим:

^Δα=^·^, (12)

или, выражая угол скоса в градусах,

Δα°=57,3~· Су-

Т. о., коэфф. И. с. может быть представлен следующей ф-лой:

- -k ΟΙ · (13)

Это—ур-ие параболы, ось которой проходит через ось^ Cf. Эта парабола называется параболой индуктивного сопротивления. Обозначим через А; тогда

C_i=A Щ. (14)

А является, следовательно, параметром па

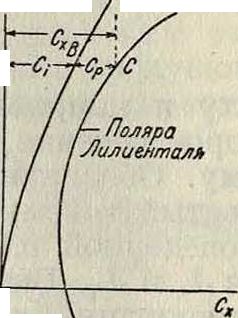
Фигура 7.

раболы И. с. и зависит только от относительного размаха λ. При увеличении Я ветви параболы будут приближаться к оси ординат—парабола будет делаться более раскрытой; при Д=оо, А—0—парабола обращается в ось ординат.

Так. обр., И. с. зависит от подъемной силы и от относительного размаха: при одной и той же подъемной силе, чем больше относительный размах, тем меньше И. с.; при бесконечном размахе И. с. равно нулю и, следовательно, все лобовое сопротивление крыла сводится только к профильному сопротивлению. С другой стороны, при одном и том же относительном размахе И. с. меняется в зависимости от подъемной силы, и при нуле подъемной силы все лобовое сопротивление сводится только к профильному сопротивлению, т. к. в этом случае И. с. равно нулю.

Поляра Лилиенталя дает характеристику данного крыла (смотрите Аэродинамика). На каком-либо угле атаки а отрезок АС, параллельный оси абсцисс, будет представлять собою ло- Пара&ла инду.чтиб бовое сопротивление дан-ного крыла (фигура 7). Для имеющегося у этого крыла л относительного размаха Я можно по формуле (13) построить параболу И. с.; тогда отрезок АВ будет представлять собою И. с. этого крыла, соответствующее, определенной подъемной⁰ силе. Отрезок ВС будет, следовательно, равен С_р, то есть профильному сопротивлению. Т. о., при помощи приведенных ф-л можно решать основные задачи теории И. с., которые находят большое применение на практике.

Одной из главных задач является нахождение характеристики крыла одного относительного размаха по характеристике крыла другого относительного размаха, или нахождение характеристики биплана или вообще полиплана какого угодно размаха по характеристике моноплана. Т. к. аэродинамич. лаборатории обычно дают характеристику монопланного крыла для относительного размаха, равного 5 или 6, то при аэродинамическом расчете самолета приходится находить характеристику крыла для того относительного размаха, который имеется на рассчитываемом самолете.

Исходя из теории П-образных вихрей в случае биплана или вообще полиплана, можно также найти все поле скоростей. Метод, данный для этого Бетцем, состоит в том, что путем последовательных приближений находят влияние одного крыла на другое при каком угодно расположении и величине крыльев; однако, он требует длительных вычислений, и поэтому мы приведем здесь лишь приближенную формулу для полипланов, данную проф. Прандтлем. Под коэфф-тами сопротивления полиплана мы будем подразумевать коэфф-ты суммарного действия планов, получающиеся по правилу смешения, то есть коэфф-ты подъемной силы и лобового сопротивления полиплана будут:

_ Су, · Si + Ci/₂ · s„ +. + Cy_n S„

^ Si + S_s+.

Qcj · Si 4- C*₂ · So -f. -f Οχ_η · S_nS_x + S_z +. + Sn ⁹

_a, Cy_n—коэфф-ты подъемной

ТТГ»Т> ΤΤ/Λ ΤΤΤΤΤΤΤΤΟ TJO ·

JC₁»

₂,., соответственно коэфф-ты лобово-

C_x =

^r«^{e С}У1’ ^су“ ^с*

щ

Фиг. силы каждого из планов полиплана; С,

с_Х2,.,а го сопротивления планов, a S_u S₂, ·, S_n— площади каждого плана.

И. с. полиплана, имеющего одинаковой ширины крылья, будет выражаться ф-лой,

. аналогичной формуле (14) j моноплана; однако, коэффициент А будет зависеть не только от относительного размаха плана, но также и от числа планов и их взаимного расположения. Для полипланов приближенное выражение для коэфф. А будет:

где I—наибольший размах полиплана, £>— несущая площадь всех планов, a F—заштрихованная площадь, показанная на фигуре 8. Если взять частный случай, когда все планы имеют одинаковый размах Ϊ, одинаковую ширину крыльев Ь, а расстояние между планами равно ширине, то общая площадь S =п·b I,

где п—число планов. В этом случае площадь F можно выразить след, обр.: F=(п — 1 )Ь I, и формула (15) получает такой вид:

А=-

π λ -j- 4(η — 1)

В частном случае, при п= 1, она переходит в формулу для моноплана, выведенную выше.

Наиболее часто применяемой на практике задачей является переход от крыла с одним относительным размахом к другому. Если мы имеем для данного размаха Я поляру Лилиенталя, то можно определить, для каждого угла атаки профильное сопротивление, то есть найти характеристику этого крыла для бесконечного размаха, вычитая из абсцисс кривой Лилиенталя абсциссы параболы И. с., построенной для значения Я. Находя параболу И. с. для другого относительного размаха Я и прикладывая к нему профильное сопротивление, найдем но-

λ х вую поляру для относительного размаха Я.

Однако, от относительного размаха зависит также и скос потока; поэтому при определенных значениях подъемной силы как при бесконечном размахе, так и при новом конечном Я углы атаки изменятся за счет различных скосов потока. Вычисление характеристики крыла | при переходе от одного размаха к другому можно делать графич. или аналитич. путем. На фигуре 9 показан графич. метод такого вычисления при нахождении самой поляры. Остается определить те углы атаки, соответствующие определенному С,.,

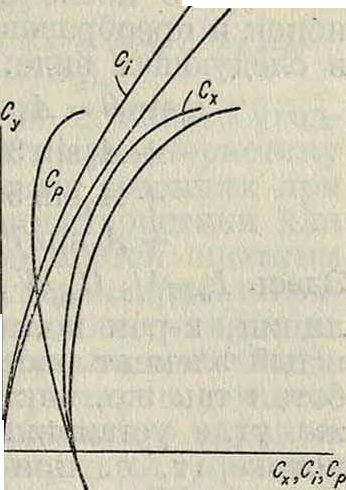
Фигура 9.

к-рые получатся при переходе от относительного размаха Я к относительному размаху Я.

Угол скоса потока выражается ф-лой:

Ьа^АСу. (16)

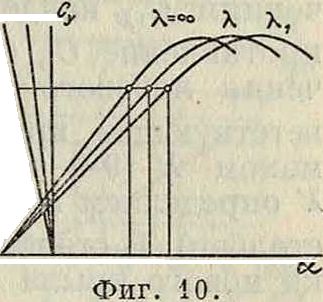
Если вычислить А для значения Я, соответствующего относительному размаху первоначальной характеристики, то можно найти скосы потока, получающиеся при этом крыле. Истинный угол атаки α —Δα равен кажущемуся углу атаки для крыла бесконечного размаха. Если мы имеем значения С_у, выражаемые кривой по углу атаки а, то, проведя налево от оси ординат прямую (фигура 10), выражаемую ур-ием (16), получим, что для каждого С_у скос потока будет выражаться соответствующей абсциссой этой прямой. Если отнести кривую С_у к вышеупомянутой прямой, то получим кривую Су по истинным углам атаки.

Если же отнести эту кривую С_у к прямой, выражаемой ур-ием Аа=АС_у, где А соответствует Я, то получим выражение С_упо углам атаки, соответствующим относительному размаху Я. По найденной характеристике С_у по а для нового относительного размаха Я можно на поляре Лилиенталя нанести и соответствующие каждому значению С, углы атаки.

Вместо только что описанных графических операций можно применить также и вычисление. Имея характеристику монопланно-го крыла определенного размаха Я, будем, следовательно, иметь соответствующиедруг другу величины а, С_у и С_х1. Вписываем“ их в первые три столбца таблицы.

Таблица для вычисления характеристики крыла при переходе от одного размаха к другому.

Так как лобовое сопротивление является суммой сопротивлений индуктивного C_t· и профильного С_р, причем С_г зависит как от относительного размаха Я, так и от соответствующей комбинации крыльев (моноплан, биплан и т. д.), а С_р—от индивидуальных свойств профиля, то переход от одного относительного размаха к другому или от одной комбинации крыльев к другой будет заключаться в соответствующем изменении И. с. С i, а также и угла атаки а для каждого С_у. Т. о., в 4-й столбец вписываются значения С_г-для того относительного размаха или для той комбинации крыльев, для которой имеется характеристика. С_г;_ определяется по формуле С_и=А_л · С?. Вычитая из общего сопротивления С_х И. с. С_и, получим профильное сопротивление С_р (5-й столбец). Углы атаки,

соответствующие определенным С_у и С_хХ, будут уже отличны от значений, данных в

1-м столбце, вследствие скоса потока. Этот скос потока, соответствующий бесконечному размаху, определяется по формуле Ла_я=А_ЛС_у (6-й столбец). Углы атаки, соответствующие бесконечному размаху данного крыла, найдутся, если вычесть из соответствующего значения 1-го столбца значение 6-го столбца (7-й столбец). Таким образом, 2-й, 5-й и 7-й столбцы дают характеристику крыла бесконечного размаха.

Для нахождения характеристики крыла другого относительного размаха Я находим И. с. для относительного размаха Я, к-рое определяется по ф-ле: С_и.=А, С| (столбец

8-й). Прикладывая к соответствующим значениям С_и, найденное уже профильное сопротивление С_р (5-й столбец), найдем значения лобового сопротивления С_хХ, соответствующие крылу с относительным размахом Я (9-й столбец). Скосы потока для Я определяем по формуле Δα_Λ,=А_х, С_у (10-й столбец). В столбец 11-й заносим углы атаки нового крыла с удлинением Я, которые получаются сложением значений столбцов 7-го и 10-го. Т. о., новую характеристику крыла с относительным размахом Я будем иметь в столбцах 2-м, 9-м и 11-м. Подобные вычисления проделываются для различных а, С_у и С_хХ в диапазоне имеющейся характеристики (обычно через каждые 2°).

Соответствующий анализ показывает, что постоянная по всему размаху скорость скоса, вызванная вихрями, получается в случае распределения циркуляции по размаху по закону полуэллипса. В этом случае И. с. и скос потока выражаются совершенно так же, как и в случае П-образных вихрей, а именно:

С_г.= А.С*иДα= 1. С,.

Т. о., средняя вызванная скорость П-образных вихрей одинакова с постоянной скоростью при эллиптическом распределении. Такое распределение циркуляции получается при эллиптической в плане форме крыльев одинакового профиля и одинаковых углов установки.

Рассмотренная выше схема П-образных вихрей является схемой искусственной; при рассмотрении сложных крыльев приходится прибегать к более точному методу, ибо эта упрощенная схема дает в таких случаях слишком неточные результаты. Кроме того, если бывает нужно построить распределение давления по крылу, то приходится уже рассматривать влияние каждого вихря на данную точку жидкости.

Ф-ла (5) дает значение вызванной выхрями скорости для любого распределения циркуляции. С другой стороны, в каждом сечении крыла должен быть удовлетворено равенство

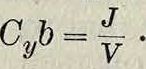
Зная в каждом сечении крыла его профиль С_у, ширину крыла b и, следовательно, кажущийся угол атаки а, можно найти в каждом сечении скос потока, а также и истинный угол атаки а₀ — а — Δα. Так как в об щем случае уравнение (5) не интегрируется в простых функциях, то для нахождения характеристики сложного крыла приходится пользоваться следующим приближенным методом. Задаются распределением циркуляции вдоль размаха крыла и определяют в каждом его сечении скос потока Δα; зная же Δα и угол атаки а, можно найти и а — Δα. Затем определяют новую кривую распределения циркуляции по формуле J=C,_JobV, где С,_л—коэфф. подъемной силы профиля данного сечения для бесконечного размаха, соответствующий углу атаки α—Δα. Если новая вычисленная кривая не совпадает с той, которою задавались вначале, то следует вновь повторить те же вычисления, задавшись другой кривой распределения циркуляции, промежуточной между вычисленной и ранее заданной. Все эти вычисления чрезвычайно кропотливы и требуют много времени; значительное сокращение дает графический метод, описанный в «Трудах ЦАГИ», 1929 г., вып. 42.

Можно пользоваться также и другим аналитическим методом—Трефца, представляющим то удобство, что он сразу дает выражение для распределения циркуляции, причем устраняется надобность в последовательных приближениях. Сущность этого метода заключается в том, что линия разрыва скоростей, являющаяся также гранящей вихревой области на крыле, преобразуется соответствующими подстановками в круг, а функция потенциала скоростей разлагается в тригонометрии, ряд и должен быть удовлетворена в нескольких точках крыла по его размаху,—это приводит к решению совместных ур-ий для определения коэффициента этого ряда. Коэфф-ты подъемной силы и И. с. будут, согласно этой теории, выражаться след, образом:

-А-1

(7.= лг. _ί_. (72

^ν πλ °У

(17)

Здесь jy₌A; + 3Af ₊ 5Ai ^{+ 7}Aj ₊ .·· _;Ai,A₂,A_s.

коэфф-ты тригонометрии, ряда разложения потенциальной ф-ии:

9 =

А_х sin 0 A₃sin 30

A₅S3n 50 A₇sin 70

Это ур-ие после соответствующих подстановок и преобразований можно представить в следующем виде:

/„sin Θ=AjSin θ(μ -j- sin θ) +

+ A₃sin39(3,« + sin Θ) +

+ A₅ sin 5Θ (5μ -b sin θ) -1-+ A,sin 76(7μ + sin Θ) +. (18)

Здесь I₀=¹/₂ C_yW, T. e. половине цирку ляции, которая получилась бы, если бы каждый элемент рассматриваемого крыла работал так же, как он работал бы при этом же угле установки в плоскопараллельном потоке (то есть при бесконечном размахе). С_Уо—коэфф. подъемной силы профиля с бесконечным размахом, Θ—угол между радиусом и осью абсцисс, определяющий положение какого-либо сечения крыла (фигура 11),

= —^g£° ^b, где ft,—угол наклона кривой

21

С_Уо к оси углов атаки для крыла бесконечного размаха.

Мы уже видели, что И. с. эллиптического крыла выражается след, обр.:

следовательно, коэфф.Х представляет собою увеличение И. с. над значением его, получающимся при эллиптическом распределении циркуляции.

Оказывается, что для целей практики совершенно достаточно бывает брать для определения коэффициентов А_г,А₃, А₅ только четыре члена тригонометрического ряда и удовлетворять этому ряду только в четырех точках; тогда мы будем иметь четыре ур-ия с четырьмя неизвестными. Для удобства вычислений можно брать сечения по-лукрыла, соответствующие значениям Θ,

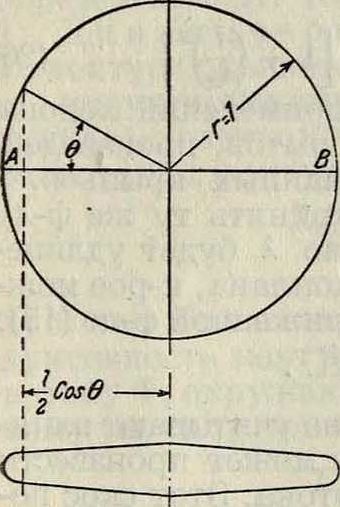
Фигура 11.

У

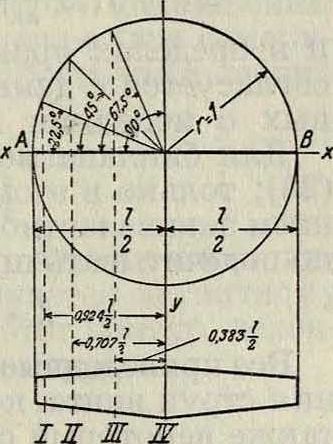
Фигура 12.

равным 22,5°, 45°, 67,5° и 90°, отстоящим от середины крыла на расстоянии соответственно 0,924 0,707 ^ ; 0,383 ^ и 0

(фигура 12). В этом случае система уравнений будет иметь следующий вид:

I. 0,383 (++0,383) А_г+0,924 (3+ + 0,383) П ₃ + +0,924 (5/*! + 0,383) А, + 0,383(7,+ + 0,383) А_?=

=0,383 («/„),;

II. 0,707 (/«2+0,707) Η,+0,707 (3/«₂+0,707) А₃--0,707 (5++ 0,707) П₅-0,707 (7/г₂+0,707)П,=

= 0,707 (J₀)s;

III. 0,924 (/i₃+0,924) Ai-0,383 (3/г₃+0,924) A_z-- 0,383(5/«₃+0,924) П₅+0,924(7++ 0,924) Д,=

=0,924 (J_u)₃;

IV. (μ₄ + 1) А_х — (3+ + 1) А₃ + (5+ + 1) А_ъ —

— (7+ + 1) -47⁼ (=10)4·

Т. о., для определения И. с. какого угодно крыла необходимо иметь характеристику профилей в рассматриваемых сечениях при бесконечном размахе. Характеристики для конечного размаха определяются опытным путем. Выше был уже изложен приближенный метод пересчета с конечного размаха на бесконечный. Этот метод, однако, являющийся точным для эллиптич. крыла, не дает возможности более точно подсчитать характеристику бесконечного размаха для крыльев других форм. В аэродинамич. лабораториях обычно испытывают крылья прямоугольные, поэтому в первую очередь необходимо уметь пересчитывать на бесконечный размах характеристики этих крыльев. Подставляя в формулу (17) значение площади крыльев S =1Ь, а также принимая во внимание уравнение (18), получим:

Г1 ____ · _Яи.__1 4 (Л Q

2bV ’ С,_л 4 + *

Кроме того, коэфф. N зависит от величины μ, так как в ур-иях I, II, III и 1Υ коэфф-ты А_г, А„, А₅ и А, определяются через μ. На фигуре 13 даны величины =+- и IV в завися-

О»

) •о мости от. По этим графикам, если известна характеристика профиля для бесконечного размаха, можно найти также характеристику прямоугольного крыла. Для решения обратной задачи на тех же графиках нанесен другой масштаб — где β—угол

Кривые поправочных Су ноэсрсрициентов для -(Г прямоугольного крыла

0,8

0,4

1,15

3

1,05

4JA

5 tj/β

									λ
					и’
			У
2 3 4 Що

2 3 4 5 fgfi

ФИГ. 13.

^для W

наклона к оси абсцисс характеристики данного профиля прямоугольного крыла. Таким же ι,οο · образом можно вывести поправочные коэффициенты для каких угодно крыльев. Однако, приближенно можно для нек-рых форм крыльев пользоваться следующими формулами. Трапецоидальное крыло (фигура 14): для отношений ~, равных от ^х/з Д° ²/з>

С.- + - Ч·

Крыло с закруглен, концами (фигура 15):

л 0,730 „

д_α=

СМ- - С*

¹ πλ У

Все вычисления по этим ф-лам производятся указанным выше способом, только при нахождении И. с. и скоса потока следует подставить вместо величины А ее новое соответствующее значение.

Как уже было указано, по теории Треф-ца распределение циркуляции по размаху

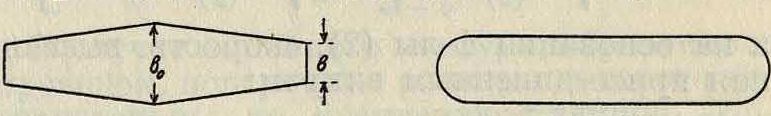
Фигура 14. Фигура 15.

можно представить в виде определенной кривой. Эта кривая выражается следующим уравнением:

J=2 (Д_г sin Θ + А₃ sin 3Θ +

+ А₅ sin 5Θ + А₇ sin 70). (20)

Когда коэфф-ты A_lt А₃, А_ь и А, определены для соответствующих Θ вышеуказанным способом, то можно построить и эту кривую.

При наличии подъемной силы крыло отклоняет набегающий на него поток на некоторый угол, а следовательно, и сзади крыла поток будет также скошен на определенный угол (фигура 16). Этот скос потока за крылом вызывается как вихревой пеленой, так и присоединенными вихрями. Так как стабилизатор обычно располагается сзади крыла, то он будет работать в потоке, уже возмущенном крылом, и угол атаки стабилизатора нельзя уже будет определять как угол между хордой стабилизатора и направлением движения всего самолета. В расчете устойчивости, когда приходится определять восстанавливающие моменты стабилизатора и, следовательно, находить подъемную силу стабилизатора, необходимо учитывать скос потока от крыльев.

Фигура 16.

Теория И. с. дает возможность найти этот скос. Кроме того, в самолетах типа тендем влияние переднего крыла на заднее выразится в изменении подъемной силы и лобового сопротивления за счет изменения углов атаки от скоса потока.

При П-образной схеме вихрей формула для скоса потока может быть выведена на основании выражения (2). Если предположить, что один конец шнура уходит в бесконечность и, следовательно, cosy₂=1, а другой лежит на расстоянии с от точки В (фигура 2), то в пашем случае выражение для вертикальной вызванной скорости примет вид:

V=— (1 - ,_1_Л (21)

4лх У X² + CV

Вертикальная скорость за крылом будет вызвана двумя концевыми вихрями и присоединенным вихрем (фигура 17). На основании принципа независимости можно принять, что общая вызванная скорость слагается из скорости, вызванной присоединенным вихрем, и удвоенной скорости, вызванной одним концевым вихрем. На основании ф-лы (21), скорость, вызванная двумя концевыми вихрями:

J Г_{1 +}

Фигура 17.

2г>.= 2-

^4,1 Υ~$ ^{+ 4} L V~(I)" ^{+ hl + a}

а на основании ф-лы (2), скорость, вызванная присоединенным вихрем:

i

J 2

V, =

2л следовательно, общая рость за крылом 1

вертикальная ско-

^ν=ί

_:+

V ©+« V^i^+h^V^i^+h‘^+at

+

+

Vhl + a-y Ч + о“+(|)‘

(22)

Эту формулу можно упростить, принимая, что возвышение крыла над стабилизатором равно нулю (Яг.!=0), что обычно и осуществляет ся на практике. В таком случае будем иметь:

^vT-irb+V <²³>

или, для скоса потока, выраженного в градусах:

_Δαο_=5Υ;3^[ι _{+ }}/ι+(!)]. ₍₂₄₎

При эллиптич. распределении циркуляции по размаху, формула для скоса потока за крылом будет иметь следующий вид:

Д«°=57,3^--С-,[ 1 + Щ·]. (25)

Обе приведенные ф-лы дают довольно значительно разнящиеся между собой результаты и не вполне согласуются с опытными данными для наиболее ходовых типов крыльев. Поэтому имеются попытки составления полуэмпирических, согласующихся с опытом формул. Одна из таких формул имеет следующий вид:

Да°=57,3 ~_лу · Су [l + (ζ)²] (26)

и в пределах практич. применений хорошо согласуется с данными опытов, произведенных с моделями монопланных крыльев.

Для биплана можно принять ту же формулу (26); только в этом случае λ будет удлинением эквивалентного моноплана, к-рое можно подсчитывать по приближенной формуле (15):

я л1² + 4F

А =----с. *

лЬ

Все приведенные ф-лы не учитывают влияния струи винта, которая может произвести также некоторый скос потока. Этот скос потока от винта с достаточной степенью точности можно определять по формуле:

<5=( --1¹ —Λ (α-β) ^Δ“

2 В 0,6

/l + 2B ’

(27)

где а—угол атаки крыльев, Да—скос потока от крыльев, β—угол наклона оси винта к хорде крыла и В—коэффициент нагрузки на ометаемую винтом площадь (смотрите Воздушный винт).

Лит.: Юрьев Б. Н., Индуктивное сопротивление крыльев аэроплана. «Труды НАГИ», 1926, вып.20; его ж е, Определение аэродинамических свойств крыльев произвольного очертания в плане, «ВВФ», 1923, 2; Саткевич А., Аэродинамика как теоретическая основа авиации, П., 1923; Че в

A. В., О построении поляры Лилиенталя моноплан-ного крыла произвольной формы, «Техника возд. флота», М., 1927, 6; «Материалы по аэродинамическому расчету самолетов», Сборн. статей под ред.

B. Александрова, «Труды ЦАГИ», 1929, вып. 42;

Козлов С. Г., Аэродпнамич. расчет бипланной коробки, «Техника воздушного флота», М., 1927, 3; Prandtl L., Application of Modern Hydrodynamics to Aeronautics, «Reports of the Nat. Advis. Comm, for Aeronautics», Wsh., 1921, 776; P r of n d 11 L. u. Betz A., Vier Abhandlungen z. Hydrodyna-mik u. Aerodynarnik (Tragfliigeltheorie, 1. u. 2. Mit-teilungen), Gottingen, 1927; Bader H. G., Flugzeug-baukunde, B., 1924; Bader H. G., Grundlagen d. Flugtechnik, B., 1920; Glauert H., A Method of Calculating the Characteristics of a Tapered Wing, «Aeron. Research Committee, Reports a. Memoranda», L., 1922, 821; Florine N., Trainee induite des aiies d’avion, «Bulletin du Laboratoire adrotechnique de Belgique», Bruxelles, 1922; Fuchs H. und Iiopf L., Aerodynarnik, B., 1922; Hunt M„ General Biplan Theory, «Reports of the Nat. Advis. Comm, for Aeronautics», Wsh., 1922, 181; S i rain ο n s L., Note on the Applications of the Vortex Theory of Aerofoil to the Prediction of Downwash, «Aeron. Research Committee, Reports a. Memoranda», L., 1924, 914; Simmons L.a. Owner E., An Investigation of Downwash in the Slipstream, ibid., London, 1924, 882. В. Апександров.