> Техника, страница 49 > Индукции закон

Индукции закон

Индукции закон, открытый Фарадеем (1832 г.), обычно формулируется след, обр.: «при изменении потока магнитной индукции, проходящего через замкнутый электрический контур, в этом контуре возникает индуктированная электродвижущая сила, пропорциональная числу магнитных силовых линий, перерезывающих за единицу времени данный контур». Число N силовых линий, или, вернее, «силовых трубок», опре-деляютт. о.,чтобыих плотность, то есть количество трубок, приходящееся на единицу площади поперечного сечения, численно равнялось магнитной индукции В, выражаемой в гауссах. При таких условиях И. з. выражается математической ф-лой:

CD

где 2 Ri—сумма падений напряжения во всех частях замкнутого контура. По закону Кирхгофа, эта сумма при отсутствии эдс должна равняться нулю; поэтому выражение — ^ называют эдс индукции. Эта эдс направлена всегда т. о., чтобы противодействовать причине, создающей индуктированный ток (закон Ленца). Картина силовых трубок, перерезывающих проводник, помогает быстро ориентироваться в распределении индуктированных токов, однако, в сложных случаях эта картина может вместо облегчения способствовать затемнению вопроса. M, действительно, большое число изобретателей под влиянием этого представления тратят много времени для создания невозможных усовершенствований, гл. обр. в области униполярных машин (смотрите Динамо машина). В настоящее время более целесообразно иначе подходить к истолкованию явлений индукции. Мы будем различать два случая: 1) когда все тела неподвижны относительно наблюдателя и 2) когда они перемещаются.

Неподвижные тела. Закон Кирхгофа применим только в случае стационар ного поля, когда отсутствуют вихри вектора напряженности электрич. поля. В этом случае все электрич. силовые линии, которые можно нарисовать в поле, имеют начало и конец. Электрич. поле создается зарядами или эдс аккумуляторов, термоэлементов и тому подобное. Закон Кирхгофа оказывается неприменимым при нестационарном поле. Если магнитный поток изменяется по времени, то это явление всегда связано с наличием вихревого электрического поля. Электрич. силовые линии, изображающие это поле, не имеют ни начала ни конца. Т. о., линейный интеграл вектора напряженности электрич. поля, или, что то же самое, электрич. напряжение вдоль замкнутой линии, охватывающей пульсирующий поток, не равно н у л ю. Скорость уменьшения магнитного потока называется магнитным спадом,

άΦ,

— (поток считается положительным в направлении, связанном по правилу штопора с положительным направлением, выбранным вдоль замкнутой линии, охватывающей поток). Поэтому И. з. в неподвижных относительно наблюдателя телах можно формулировать след, обр.: электрическое напряжение U по замкнутому контуру, охватывающему магнитный поток, равняется магнитному спаду. В знаках:

U=-f (2)

ИЛИ

f E dr=-i jsds. (3)

L S

Taii как, по теореме Стокса,

j) Е dr=J rot E dS,

L S

то формулу (3) можно выразить в дифференциальной форме в виде ур-ия

_{rotjB =} _f. (4)

Это—одно из ур-ий Максвелла. Электрич. поле связано с пульсирующим магнитным потоком независимо от наличия проводников в поле. Если насадить на стержень трансформатора кольцевую вакуумную трубку, то движение электронов, находящихся в этой трубке, будет ускоряться в вихревом электрич. поле, окружающем трансформатор. Если заменить вакуумную трубку обыкновенным медным витком, то этот медныйвиток будет играть роль зонда, позволяющего обнаружить наличие электрич. поля, существовавшего вокруг трансформатора и до помещения витка. Напряжение обхода в этом витке отлично от нуля не потому, что в нем возникает эдс, а потому, что поле переменного тока, существующее в трансформаторе, не статическое, в нем нет потенциала, и напряжение обхода по замкнутому витку равно магнитному спаду. Формально магнитный спад играет роль эдс. Когда говорят об индуктированной эдс, то этим хотят для удобства нестатическое электрическое поле формально рассматривать как статическое. Правильнее говорить об индуктированном напряжении,

а не об эдс, ибо на самом деле в цепях переменного тока обыкновенно не бывает эдс. За последнее время, в особенности в германской литературе, часто встречается выражение «индуктированное напряжение» вместо «индуктированная эдс».

Это утверждение можно пояснить следующим примером. Если замкнуть на себя ряд последовательно включенных гальваническ. элементов через равномерно распределенные сопротивления, то напряжение между двумя любыми точками образованной т. о. цепи не превышает напряжения одного элемента.

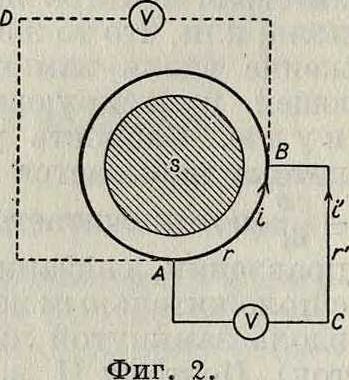
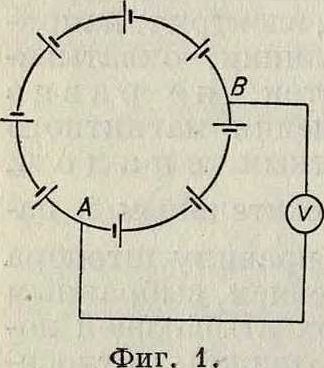
Чтобы в этом убедиться, достаточно присоединить вольтметр к двум точкам 1 и В рассматриваемой цепи (фигура 1). Электрич. поле, окружающее элементы, определяется силовыми линиями, идущими от положительных полюсов к соседним отрицательным. Во многих учебниках такое расположение в последовательно включенных элементах приводится для объяснения явления индукции. Если, наир., вокруг стержня трансформатора поместить замкнутый виток, то в этом витке появляется электрич. ток. Этот виток охватывает магнитный поток,пульсирующий через сечение S стержня трансформатора. Эдс, возникающую в витке, представляют себе равномерно распределенной по всему витку. Получается как бы последовательное соединение бесконечно большого числа бесконечно малых эдс. Эдс, возникающая в отрезке АВ витка, в точности компенсируется падением напряжения в этом отрезке. Т. о., «разность потенциалов» между любыми точками А, В нашего витка должна равняться нулю. На самом деле, однако, вольтметр, присоединенный к точкам А, В, покажет напряжение, причем это напряжение будет различным в зависимости от того, как присоединить провода к вольтметру. Вольтметр, включенный в контур И СВ "(фигура 2), покажет другое напряжение, чем вольтметр, включенный в контур ADB. Рассмотрим контур АВСА. Предположим, что ток г достаточно мал и что мы поэтому можем пренебрегать потоком рассеяния, проходящим через поверхность, окаймленную контуром АВСА. Тогда, по закону Кирхгофа,

гг — гг=0, или гг=гг.

Если бы в отрезке АВ имелась эдс Елв=гг, то мы имели бы г=0, то есть вольтметр не показывал бы напряжения.

Следует упомянуть, что В. Ф. Миткевич придерживается другой точки зрения, сильно распространенной среди ленинградских инженеров-электриков, и считает, что явления индукции создаются реально существующими магнитными кольцами (смотрите лит.).

Движущиеся тела. Движение тел в постоянном магнитном поле следует рассматривать не так, что тела эти «перерезают» магнитные силовые линии или трубки. Нетрудно доказать, что самое существование таких трубок противоречит ур-иям Максвелла. Т. к. каждое магнитное поле создается электрич. токами (движением электронов или токами смещения), то всегда можно определить движение данного тела относительно этих токов. Рассмотрим движение электрона со скоростью V в поле магнитной индукции

В. Обозначим через — е заряд электрона. Тогда во время движения на него будет действовать сила, равная векторному произведению —e[vB], Если в постоянном магнитном поле движется материальное тело, например медный стержень А_ХА₂, то на каждый его электрон или протон будет действовать соответствующая сила, зависящая от скорости движения данной частицы.

Эта скорость является суммой двух скоростей: скорости V переносного движения стержня, общей для всех его точек, и скорости v_x, раз- ф_ИГ. з. личной для каждой частицы. При статистическом (макроскопическом) рассмотрении явления скорость v_xможет быть оставлена без внимания, потому что в сумме для всех частиц, беспорядочно движущихся в стержне, скорости v_xне дают видимого изменения тела. Поэтому можно рассматривать явление т. о., как если бы благодаря движению стержня на все его электроны и протоны действовало электрическое поле с напряженностью [vB] (сила, действующая на единицу положительного заряда). На фигуре 3 скорость v_LВ; поэтому электрич. поле будет иметь напряженность vB и будет толкать протоны по направлению [vB], а электроны—в противоположном направлении, то есть к точке А_х. Протоны будут оставаться на месте, а электроны будут накопляться в А_х и уходить из А₂. Т. о., в А_х будет возникать отрицательный заряд, а в А₂—положительный заряд. Эти заряды создают электрич. полеЕ,направленное от А ₂ к А_х, то есть противодействующее полю [vB], Равновесие наступит тогда, когда в каждой точке Е будет в точности компенсировать [νΒ], то есть когда будет откуда

E=vB.

Если стержень имеет длину Ϊ, то, т. о., между концами его благодаря зарядам возникает электрич. напряжение U, равное линейному интегралу вектора jЕ, т. e. U=Bvl. Если во время движения соединить концы стержня при помощи скользящих контактов с зажимами вольтметра, то вольтметр покажет напряжение U. То же напряжение возникает и в стержнях динамомашины и называется обычно «эдс вращения». Рассмотрим теперь медную шайбу (фигура 4), вращающуюся в постоянном магнитном поле с угловой скоростью со. В этом случае опять на каждую ча-

А,

стицу будет действовать в среднем электрическом поле [vB], Это поле направлено радиально и притом, при выбранном направлении скорости V, от центра к периферии; следовательно, электроны будут накопляться вблизи центра до. тех пор, пока возникшее радиальное поле Е, направленное от периферии к центру, будет компенсировать поле [vB]. Тогда в любой точке на расстоянии г от оси вращения будет Е=Всог.

Следует отметить, что в этом случае div E=div В wr=2 Βω.

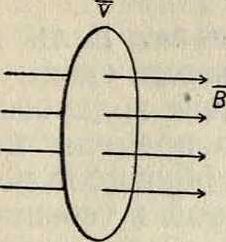
Фигура 4.

Т. о., внутри вращающегося цилиндра будет равномерно распределен электрич. заряд. Однако, плотность этого заряда ничтожна и равна 2· 0,884Всо 10-^!‘ С/см“.

Это поле создает электрич. напряжениевдоль любого радиуса от периферии к центру:

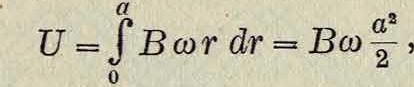
где а—радиус шайбы. Если установить в центре шайбы и на периферии два скользящих контакта, то по проводам, соединяющим эти контакты, пройдет электрич. ток. Аналогичное рассуждение позволяет определить электрич. напряжение, возникающее между осью и боковой поверхностью цилиндрического магнита, вращающегося вокруг своей оси (фигура 5).

В перечисленных случаях форма тела давала возможность установиться в данном магнитном поле определенному равновесию. Нетрудно убедить- г---1*

ся, что в общем случае такого равновесия не бывает и при движении тел в магнитном поле воз- -----»

никают электрические токи. Когда тело вращается с угловой скоростью ω вокруг оси, параллель- ΤΤΤ^ί ной единичному вектору к в маг- _фиг_ ₅_ нитном поле В, то в этом случае создается внутри тела вихревое электрическое поле, причем

rot Е=[Всо],

где со=/ссо. В предыдущих примерах было [Вш]=0. Если же Б направлено под углом к ω, то в теле возникают вихревые токи, точное вычисление которых в общем случае весьма затруднительно. Если тело движется в магнитном поле, изменяющемся по времени, то при вычислении индуктированных токов надо учитывать изменение потока, происходящее по двум причинам; изменение во времени индукции В и изменение положения тела. Создаваемые т. о. вихревые поля просто накладываются друг на друга, и rot Е получает в любой точке движущегося тела выражение

rot Е=— -gj- + rot [г>В],

где V—линейная скорость движения рассматриваемой точки. Интегрирование этого ур-ия представляет весьма большие трудности, но в практических задачах электротехники приходится большей частью встречаться с такими формами, где это интегрирование чрезвычайно упрощается.

Лит.: Поль Р., Введение в учение об электричестве, М.—Л., 1929; Тамм И. Е., Основы теории электричества, т. 1 ,М.—Л., 1929; МиткевичВ.Ф., Физич. основы электротехники, ч. 1, М.—Л., 1928; Эйхенвальд А. А., Теоретич. физика, ч. 1— Теория поля, М.—Л., 1928; С о li n E., Das Elektro-magnetisehe Feld, В., 1927; Abraham M., Theorie d, Elektrizitat.B. 1, 7 Aufl., B.—Lpz., 1923; Dissel-h о r s t, Elektrodynamik, Handbuch d. Elektrizitat u. d. Magnetismus, hrsg. v.L. Graetz, Leipzig, 1918—23; S p i e 1 r e i n J„ Lehrbuch der Vektorrechnung, Stg., 1926; S p i e 1 r e i n J., tJber ungeschlossenen Wirbel-linien, «Arehiv fur Elektrotechnik», Berlin, 1926, В. 17; Gans R., Einfuhrung in d. Vektoranalysis, 5 Aufl., B.—Lpz., 1923; Frenkel J., Lehrbuch der Elektrodynamik, B. 1—2, B., 1926—28. Я. Шпильрейн.