> Техника, страница 49 > Инерция

Инерция

Инерция, свойство массы удерживать свое состояние покоя или прямолинейного равномерного движения.

1-й закон Ньютона гласит: «Всякое тело удерживает свое состояние покоя или равномерного и прямолинейного движения, если оно не понуждается приложенными силами изменять это состояние» [^Х].Т. о., неподвижная масса сопротивляется переходу в состояние движения, а двигающаяся масса сопротивляется изменению: а) направления и б) величины своей скорости. Появляющаяся при этом сила сопротивления массы есть сила И. Она пропорциональна и противоположно направлена ускорению движения массы. Т. к. при изменении скорости по направлению получается центростремительное ускорение j_c=—, то масса m проявляет центробежную силу И. Н_с =— т—· При изменении ate величины скорости возникает тангенциальное ускорение j_t=и тангенциаль ная сила И. Il_t=— m _dl- Здесь v—скорость центра массы, а г—радиус кривизны его траектории. Полное ускорение точки складывается геометрически из переносного, относит, и поворотного (Кориолиса). Поэтому возможны: тангенциальная и нормальная (центробежная) силы И. тела в переносном или относительном движении, сила И. его в поворотном движении И_к=т 2мо> sin а (смотрите Ускорение Кориолиса) и тому подобное.

Хотя силы И. возникают во время движения системы, однако, по д’Аламберу, они уравновешиваются со всеми остальными силами, действующими на систему, и поэтому их можно включать в уравнения равновесия:

2(*+«5)-о. Σ(г,+-»§)-»;

2(ζ, + »5)=ο.

Здесь X, У и Ζ обозначают силы, действующие на систему по осям х, у и ζ, а индекс г сокращенно изображает ряд однородных величин с индексами 1,2,3 ит.д. Если сила И. Ж имеет плечо ρ по отношению к данной точке, то И ρ называется моментом силы И. Интегралы

i г

J dm ρ²=θ_χ и J dF о²=l_x

О О

выражают соответственно моменты И. массы и площади относительно оси х.

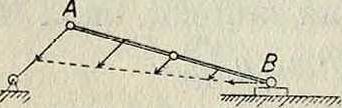
Пусть рычаг АВ (фигура 1) вращается вокруг оси 0 неравномерно, причем имеется угловое

dz_a

ускорение. На расстоянии ρ от оси вращения выделим элемент массы dm. Так как дифференциальное перемещение этой массы ds=ρ· da, то элементарная тангенц. сила И.

йИ=dm · ^=dm ρ ~

Дифференциальный момент этой силы относительно оси вращения

dM_u=dll ρ=dm · ρ³^,

откуда

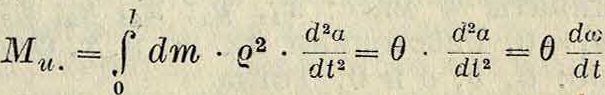
Ур-ие прочности относительно сечения ξ—£: M_U=W а=

Здесь видна конкретная связь между моментом силы И., моментом И. поперечного сечения бруса^- и моментом И. массы его. Пусть 6=ш · а²; в таком случае а называется р а-д и у с о м инерции.

И. в машинах проявляется во всей сложности, в особенности в периоды разгона и торможения машин.

Кроме того, у большинства механизмов, даже при равномерном движении приводного вала, звенья двигаются с пульсирующими скоростями, место непрерывная о г

Фигура 1.

вследствие чего имеет игра сил И. Вычисление И. в машинах приходится вести особо для каждой детали, имеющей свое собственное движение, причем можно отметить три характерных случая: а) все точки звена перемещаются параллельно друг другу с равными ускорениями, б) все точки вращаются около одной оси и в) каждая точка звена имеет свое ускорение по величине и по направлению. Случаи (а) и (б) встречаются, наприм., в экипажах, когда корпус экипажа перемещается поступательно, а колеса его вращаются; так, например, решается вопрос об инерционном сопротивлении поезда. Пусть

ds

G—вес состава, v =

dt

-его скорость, R-

радиус колес, п—число осей, Θ—момент И. массы одной оси вместе с двумя колесами. Тогда И. поступательного движения

_и _ G <Ps _ G dv ~ 9 dt² g di

Суммарный вращающий момент от сил инерции колес

Т1 ,г Л do) Θ dv

Μ„.=η·θ· _ш=п-_и· _αι·

Следовательно, сила тяги, потребная на преодоление И. поезда,

^(G- + n~ в ¹ R·

)·

Фиг.

Р =i^G

“ 9

Примером для случая (в) может служить обыкновенный шатун механизма паровой машины. Каждая точка такого шатуна (фигура 2) имеет свое собственное ускорение по величине и по направлению, благодаря чему И. приходится учитывать по поступательному движению центра массы и по вращению шатуна около этого центра. В последнее время особенно часто применяется метод замены распределенных масс шатуна группой масс, сосредоточенных. Эти последние, очевидно, должны удовлетворять условиям статики и динамики. Именно, для плоских механизмов имеем 4 таких условия, и, следовательно, достаточно взять 4 сосредоточенные массы на шатуне. Пусть Ж— масса всего шатуна, М_и Ж₂, Ж₃, Ж₄—сосредоточенные массы, к-рыми заменяется распределенная масса Ж. Координаты 4 масс: х_г, у_г х₂, у₂ х₃, у_я ^х4=2/4=0. Расстояния их до ц. т. соответственно: а, b, с и 0. Тогда

М_г + М₂ + М, + Ж₄=Ж,

М_лх₃ + М₂х₂ + М₂х,₃=0,

М.₁у₁ + М₂у, + М₃у._л=0,

М_±а² + М₂Ь°- + М₂с²=Θ, где Θ—момент И. массы шатуна относительно его ц. т. При симметричных шатунах одно из ур-ий этой группы выпадает, благодаря чему остаются только три ур-ия,и, следовательно, достаточно брать всего три сосредоточенные массы. В этом случае получается: Ж] + Ж, + Ж₄=Ж,

V/,<ι -[- М₂Ь=О,

М_га² + М₂b²=0.

Обычно М_г помещают в пальце кривошипа, Ж₂—в головке крейцкопфа, а Ж₄—в ц. т. шатуна. Скорости и ускорения этих трех точек определяются при любом расположении механизма при помощи планов скоростей и ускорений. Таким образом, получаются силы И. этих масс.

В нек-рых случаях, когда движение детали координируется не по времени, а по пространству, удобно устанавливать связь силы

И. с кинетической энергией этой детали. Действительно, кинетическая энергия

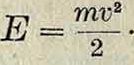
Дифференцируя это выражение: dE=mv dv=ж · * · dv, где v—скорость, a s—путь исследуемой точки, получаем:

dE dv · _ΤΎ

-г-=ш · -гг=т · 7=И. ds dt ^J

Т. о., сила И. равна производной кинетич. энергии по пройденному пути.

У современных быстроходных машин силы И. достигают нередко очень больших величин. Для примера определим силу И. паровой турбины. Пусть масса ее имеет по отношению к оси вращения эксцентриситет всего в 1 миллиметров, вес диска 20 килограмм, а число оборотов η=20 000. Тогда

И_с=ш · ω²

20 π³ · 20 000³

98T-lS0^a—

0,1 e; 9 000 килограмм.

Сила эта настолько велика, что, очевидно, даже самый малый эксцентриситет в 1 миллиметров создает непреодолимые трудности в построении прочных размеров для таких быстроходных валов. Как известно, вместо прочных валов в таких случаях конструируют гибкие валы (смотрите Вибрации). Известно не мало случаев а маховиков под действием центробежной силы. Поверочный расчет на разрыв по диаметральному сечению в этом случае дает:

Д³- δ ю“

Так, при R=200 см, п=300 и 6=7,2, получим a si 250 килограмм/см². Такое напряжение для чугуна нужно считать недопустимым. Обратно, из той же ф-лы при в=100 килограмм /см² получается предельная окружная скорость маховика v=36 м/ск.

Лит.: >) Newton I., Philosophiae naturalis principia mathematica, 2-й вариант перев. А. Крылова. «Известия Морской академии», II., 1915. А. Малышев.