> Техника, страница 49 > Интегральное исчисление

Интегральное исчисление

Интегральное исчисление, отдел исчисления бесконечно малых (смотрите), ставящий задачей вычисление и исследование свойств интегралов от ф-ий.

Неопределенный интеграл. Нахождение неопределенного интеграла есть задача, обратная дифференцированию. Если производная от ф-ии F(x) есть /(ж), то F(x) по отношению к /(ж) является первообразной ф-ией, или неопределенным интегралом. Это записывается так:

F(x)=J f(x)dx.

Ясно, что F(x)+C, где С—произвольная постоянная, есть также неопределенный интеграл, так как

£[*(*)+ CG-£*(*)-/(*)·

На основании теоремы Лагранжа о конечном приращении (смотрите Дифференциальное исчис ление) доказывается, что и обратно—всякая первообразная ф-ии /(ж) выражается в виде Р(ж)+С, где F(x) —какая-нибудь первообразная ф-ия, С—произвольная постоянная (постоянная интеграции). Записывают это так:

J/(ж) dx= F(x) + C.

Здесь fix) называется подинтегральной ф-ией,а/(ж)сгж—подинтегральным выражением. Основные формулы дифференциального исчисления дают, в силу связи между дифференцированием и интегрированием, следующую таблицу элементарных формул И. и.:

^{х dx}=ЕТТ + ^С ’ ^ПР^И

/^=1пж+С;

J е^х dx=е^х + С ;

Г а^х dx=+ С ;

J sin ж dx=— cos ж + С ;

J* cos х dx=sin ж -f С ;

Г=— ctg ж + С;

J sm^!x ^{а 1} ’

f^c^^x + C·,

/rfb^{=arcsinaj + c,;} f ifh=^arc +

/т&^{=1п(ж+1/ТТ}^^)+с·

Из соответствующих правил дифференциального исчисления легко выводятся следующие правила интегрирования: 1) постоянный множитель можно вынести за знак интеграла; 2) интеграл алгебраич. суммы равен алгебраич. сумме интегралов.

Примеры.

, _1 А

1) J=х ² dx=6x‘ +С=6]/х + С,

2) (*⁵ — 2ж⁴ + Зж³ — Зж² + 4ж — 5) dx =

= ~ -1 ж⁵ +1 х¹ — ж³ + 2 ж² - 5ж + С.

DO 4

Если можно каким-либо преобразованием представить подинтегральное выражение в виде суммы таких, интегралы которых известны, то мы получим искомый интеграл как сумму интегралов.

Пример.

/dx _ Г (sin²x + cos²x)dx _ п dx, sin² х cos² х J sin² x cos² x J cos² x ‘

+ /йп^=^^Ж-^С^^Ж + ^С· Интеграция при помощи подстановки. Если дан J* f(x)dx и если введем новое переменное t ур-ием χ=φ(ΐ), то имеем равенство:

J fix) dx=J /[>(<)] φ ΐ) dt.

Справедливость ф-лы доказывается дифференцированием. В простых случаях можно

8

Т. Э. m. IX.

не вводить новой буквы для вспомогательного переменного.

Примеры.

·>

dx

а² + Ь²х² dx

полагаем: х—~, dx=| dt; dt

f ⁼a!bf nrt5 ⁼ ^^{arCtg< + C,=}

,rctg^+ C.

·sin x dx p d cos x

2) ftgxdx=f^s™A^=f _cosx(здесь опускаем подстановку: cos*

= In cos x + G t).

3) sin² x dx=dx =

= J g dx — J* ^ cos 2ж do:; подставляя 2x=t, получаем:

I — j J cos 2ж й(2ж)=I — у sin 2ж + С.

Интегрирование по частям. Этот способ является следствием правила дифференцирования произведения: d(uv)=udv + + vdu, откуда J*и dv=uv — Jv du.

Если в заданном интеграле представим подинтегральное выражение в виде и dv, то может случиться, что f v du представит собой уже известный интеграл или, по крайней мере, будет проще данного; тогда метод оказывается целесообразным.

Примеры.

1) f хе^х dx; полагаем х=и, e^xdx=dv, тогда v=е®, du=dx и J хё^х dx=же® — J e^xdx=же® — -е^х+С.

2) J arc tga; йж; полагая ’arctg®=M, dx=dv, находим:

, п x dx, 1 f* d (1 -f X²)

«arctgж-J —=_Жагс tgx-_ff _1+χγ—

= x arc tg x — ~ In (1 + ж²) + C. Интегрирование рациональных функций. Требуется вычислить dx,

где f(x) и F(x)—многочлены. Если степень fix) больше (или равна) степени F(x), то при помощи деления выделяем многочлен, к-рый мы умеем интегрировать; остаетсяJ’JJ— dx,

где степень многочлена φ(χ) меньше степени F(x). Разлагаем F(x) на множители:

К(ж)=(ж — «)%ж — й/. (α&Ι, /Зз=1, .). Доказывается, что дробь м. б. представлена в виде суммы простых дробей: р(х)__j_ л, ^Аа,

Пх)

в,

х - Ь

(.х - а)‘ В.

(х - а)а

Bit

(х-bУ ^{1 1} W

Интегрирование каждой из этих дробей не представит затруднений, например:

f^Ax^A₁ln(x-a)+G;. J j^r_cdx =

= А_к J (ж—а)~^к dx= - ^А,‘

- fe + 1 (X-G)·-1 + ^C^

Коэффициенты A_lt В_и В₂,. опреде ляют, приводя дроби к общему знаменателю и приравнивая в числителях коэффициенты при одинаковых степенях ж.

Пример. f~j_:Имеем:

X^s +1 а, в

dx.

x(x-l)² х ¹ х-1 ¹ (х-1)^2_

А(х - 1У + Вх (х - 1) + Сх х(х - I)²

Сравнение коэффициентов дает: при ж², А + В=1; при ж, — 2А — В+С=0; свободный член А=1. Отсюда 5=0, С=2. Подставляя и интегрируя, находим:

Г ^{χ8 + 1} г1т= Г ^-и 9 Г.

J х (χ -1)^{2 ах} J *+“J (х -1)^!

= In ж — ~г[ + С.

В случае, если ур-ие F(x)=0 имеет мнимые корни, знаменатели простых дробей будут содержать мнимость; но если все коэфф-ты многочленов φ(χ) и F(x) действительны, то наряду с комплексным членом будет другой, ему сопряженный; складывая их, мы получим действительное выражение; пусть α==p+qi, А_Х=М+Ш; тогда, необходимо, β==p—qi, B_X=M — Ni; складывая, имеем:

М + Ni, М — Ni _^ М (х — р) — qN

(х - р)² + q²

х - р - qi ¹ х — р + qi

Интеграция дает:

J (х-о×— β]

~^2Nf (x-t)H^^=Mln[(a;~^P)3 + g^2]~

x - р

ΊΓ

pj dx= M J

(X - p)²+ ’

— 2N arc tg

2 (x - p) dx (x -РУ+ q^z

c.

Интегрирование иррациональных функций. Дан интеграл т₁ т_г

f R [ж, (ах + Ь)”¹, (ах + 6)^Пг,.] dx,

где R—рациональная ф-ия своих аргументов. Пусть N—общее наименьшее кратное чисел щ, «₂,.; делаем подстановку аж+Ь =

тогда

dx-Z-F-df,

п. ⁷ а

(ах + bУ⁴=t^M, (ах + b)^h=t^M.

(М_х=Ν —, М₂,. — целые числа).

Интеграл примет вид:

(t^N-±_{t t}M.

’ ’ ’ J a

где подинтегральная функция рациональна.

dx

+ χί

Подставим ί⁶=ж;

Пример. получим:

⁶J^=⁶/(¹-ⁱ + ⁱ²-iT?)^di =

= 6t - 3ί² + 2ί³ - 6 In (1 + t) + C =

= 6ж» - Зж⁴ + 2ж^ - 6 In (1 + ж¹) + С. Рассмотрим J* R(x,y) dx, где Д—рациональ ная функция аргументов, y=Va-f йж + сж². Для приведения подинтегрального выражения к рациональному виду служат три эйлеровы подстановки:

1) Если корни а и β алгебраич. трехчлена действительны, вводим переменное t ур-ием:

Ус (х — а) (ж — β)=(х — a) t ; х и у выразятся рационально через t.

2) Если о0, то можно положить:

У а + Ьх + еж²=t + х Ус.

3) Если д>0, можно положить:

У а + bх сж²=Va + tx.

Во всех случаях подинтегральная ф-ия будет рациональна относительно ί.

Пример. Г —¹——. Применим 2-ю под-J У х“+А

становку: у=Ух² + А=— ж + ί; отсюда 2t > 2t^{2 ατ} ’ » at

ж=-

Получаем

J* j=In t + С=In (ж + γχ² + Α ) + С.

Наконец, рассмотрим J х^т(а+bх^п)^р dx (интеграл от дифференциального бинома); т, п, р—рациональные числа. Если р—целое, то подстановка x=t^N, где Ж—общее наименьшее кратное чисел т и п, приведет к рациональной функции. В противном случае подстановка а + bх^п=4 приведет к интегралу

nti J (j) ^— ь) ^И ^ ’ который, по предыдущему, можно привести к рациональному виду, если — целое число. Наконец, данный интеграл можно записать в виде: j’ _хт+пр (p- -aX~ⁿ)^pdx, и он может быть при-

m + nv + 1

веден к рациональному виду, если---,

то есть + р, есть целое число. К интегралам иррациональных ф-ий относятся т. н. эллиптические интегралы вида f R(x, y)dx, где у есть корень квадратный из многочлена 4-й или 3-й степени; они не выражаются в элементарных ф-иях (смотрите Эллиптические функции).

Интегрирование трансцендентных функций. Для интегралов тригонометрии. ф-ий JR (cos ж, sin ж) dx (где R— рациональная ф-ия) всегда приводит к цели подстановка: 2=tg~; тогда еш х =:

2 Z

1 + г“ Пример.

1 - Z². _д 2 dz

^cos®=г+?·; ^dx=i~z>

Г dx	fl-f z2	2 dz _ Г
J sin х ~ t	) 2 z	’ 1 + z* J

= J^=ln2 + C =

— lntgf +C.

В отдельных случаях можно этой подстановки избежать, например:

Г sin² ж cos³ х dx=j sin² ж (1 — sin² ж) d sin ж =

sinx

з

+ С;

1шк=S дк · snk~/С¹ + ctg²x)d ctg ж =

— ctgs-^ + σ.

Фигура 1.

Рассмотрим еще интеграл:

I=J е^ах cos Ьх dx.

Две интеграции по частям дают:

I=е^ах I sin Ьх — е^ах sin Ьх dx =

= е^ах sin Ьх + ^е^т cos bх-~1.

Решая это ур-ие относительно I, получаем:

_т е^ах (a cos bx + b sin Ьх)

^{1 =} о“+ Ь*

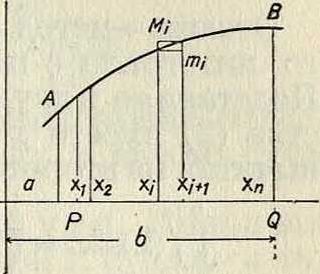
Определенный интеграл. Исторически И. и. возникло в связи с решением геометрия. задачи—найти площадь криволинейной фигуры. Пусть нам дана кривая y=f(x); предположим, что ее ординаты положительны; требуется определить площадьРД-BQ. ограниченную сверху кривою, снизу осью абсцисс, а с боков—ординатами, соответствующими х=а и х= Ь (фигура 1). Делим отрезок PQ на п частей точками ж_1; ж₂,.·.,

х._п_! (обозначим а через ж„, 6—через ж_и); из точек деления восставляем ординаты; искомая площадь разделится на полоски. Площадь полоски" с основанием, равным ж_г+1 —ж_г-= 4ж_г, заключена между площадями двух прямоугольников, из которых больший имеет высоту М_{, равную наибольшей ординате в промежутке (ж_г, ж,₊₁), меньший т_{—наименьшую ординату. Вся площадь заключена ме-

П-1

жду двумя суммами: V М_{ Δ ж_; (по избытку)

п-г и m_i x_i (по недостатку). Доказывается,

г=0

что когда п безгранично увеличивается и длины интервалов стремятся к нулю, обе эти суммы имеют общий предел, называется определенным интегралом ф-ии /(ж) в пре-

ь делах от а до Ь; его записывают так: J* f(x)dx;

а он представляет собой площадь PABQ (если ординаты кривой отрицательны, определенный интеграл дает величину площади со знаком —). Мы предполагали а<Ь; пусть теперь а>Ь,—все рассуждения сохраняются, ноДж_г будут отрицательны, и мы получим

b а

fix) dx=- fix) dx. а b

Отметим еще 3 формулы:

а b с Ь

//(ж) dx=0 ; J fix) dx=J (ж) йж + Jfix) dx ;

jfix) dx=f (ξ) (b-a),

a

где ξ—нек-рая промежуточная точка интервала (а, Ь) (теорема о среднем значении).

Связь определенного интеграла с неопределенным. Предположим, что верхний предел определенного интеграла переменная величина сам интеграл станет функцией этого верхнего предела: х

F(X)=Jf(x) dx.

а

Вычислим производную от F(X) по X: x + h х

F(X + h)-F(X)= //(ж) dx -//(ж) dx =

a а

X + h

= J fix) dx=h /(I) x

(по теореме о среднем значении);

F(X) - lim^{F(X + fe}>--^=Пт ({)=f(X).

h-*o ^h h^>0

Эта производная есть подинтегральная ф-ия, следовательно, определенный интеграл с переменным верхи, пределом есть первообразная ф-ия, то есть неопределенный интеграл:

J/(ж) dx=J/(ж) d(x) + С=F(x) + С. (2)

а

Отсюда—метод вычисления определенного интеграла с помощью неопределенного. Подставляя в двух последних частях равенства (2) вместо ж последовательно а и Ь и вычитая из второго тождества первое, найдем

f fix) dx=F φ) - F (α)=[F (ж)] *

а

(последнее выражение читается: F(ж) с подстановкой а, b).,

2

Пример. Р™=[1пж]²= In2.

J×¹

1

Ф-лы для интегрирования суммы, для постоянного множителя и интеграции по частям в случае определенного интеграла напишутся так:

b ь ь ь

J (и + V — w) dx=J* и dx + J v dx —J w dx ;

a a a a

b b

J cf(x) dx=c f f (x) dx;

a a

Ь b

J uv dx=uvY_a — J vu dx.

a a

При интеграции с помощью подстановки: x=q>(t) надо вычислить те значения t, которые соответствуют значениям х=а, ж =Ь; пусть это будут i„, ii. Тогда ь t,

J fix) dx=J f [φ (ί)] Ψ it) dt.

*•0

a _

Пример. J* У a² — x²dx.

0

Подстановка: ж=asini; dx=a cos tdt.

При ж=0, ί=0; при ж= a, i=|. Т. о.,

П 2

а² — x²dx=a²J cos²1 dt -=

0 n

„rt. Sin 2tl~ _na ^a U"⁺ 4 J₀ 4

Мы вычислили, таким обр., площадь ^х/₄ круга

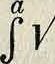
0

(у=-f У а² — ж² есть уравнение верхней полуокружности с радиусом a и с центром в начале координат). Т. к. ур-ие эллипса можно написать в виде: у =^Уа² — ж², то площадь эллипса равна лаb.

Теоремы о среднем значении. 1) Пусть /(ж) и φ(χ)—непрерывные ф-ии, причем φ(χ) > 0 в интервале (а, Ь), тогда 6

J/(ж) φ(χ) <2ж=(f) J φ (ж) dx,

a ci

где ξ—нек-рая точка между а и b.

2) Пусть <р(ж) положительна и убывает между а и Ь; тогда

6 i

J f (ж) Ψ (ж) dx=φ (a) J f (ж) йж,

Λ Cl

где a < I < b. Если φ{χ) убывает, не оставаясь положительною, то ^ δ

/(ж) 9>(ж)йж= у (a) J (ж) dx + φφ) J f{x)dx.

а а ξ

Несобственные интегралы. Иногда можно определить интеграл, если подинтегральная ф-ия не остается непрерывной. Пусть, в частности, /(ж) обращается в оо при ж=а; тогда, если

Jf(x) dx=F(x), мы определим ь ь

J /(ж) dx=lim f f (ж) dx=F(b) — lim F(a + ε),

a e-Mia + s ^ε~*°

если этот предел существует.

Приме

»!

; подинтегральная ф-ия у X

бесконечно велика при бесконечно, малом х; имеем:

lim Г -+Z=lim [2 УхТ_е=2 — 21im Уе—2.

Г* s-*o

Часто приходится также рассматривать такие интегралы, у которых один или оба предела бесконечности. Они определяются также с помощью понятия предела, например:

J fix) dx=lim J fix) dx.

Примеры.

» ь

J dx=lim J e~^x dx=[— e^_x]_o=1;

O 6->oo ₀

= [arc tg ж]^=arc tg (+ oo) —

- arc tg (- oo)=2 — (-1)=^π ·

Приложения простых интегралов. Площадь, ограниченная плоской кривой. Мы уже видели, что площадь криволинейной трапеции PABQ (фигура 1) выража-ь ется интегралом |* /(ж) dx. Более сложные а площади приводят делением к площадям

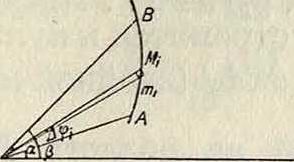
Фигура 2.

рассмотренного вида. Иногда выгодно применить полярные координаты. Пусть ур-ие кривой г=/(?>). Площадь сектора (фигура 2) АОВ разбиваем на п элементарных секторов с углами при вершине <P_t. Каждый такой сектор представим по избытку и недостатку как круговой, по ф-лам ~ Μ] λφ и |ηή Δ<ρ, где

М,- и m_t—наибольший и наименьший радиусы-векторы. В пределе при п-»ссполучим: β β

площадь АОВ=* г² άφ=~ J [/(?>)]² d<p.

а а

Если замкнутая кривая окружает начало, за пределы интеграции принимают 0 и 2я.

Пример. Ур-ие круга в полярных координатах г=а. Площадь круга равна

2 я

2 J α² άφ=π а².

О

Длина дуги. Дифференциал дуги (смотрите Дифференциальная геометрия) ds== Vdx² + dy². Если кривая задана ур-ием у== /(ж), то ее дуга между точками с абсциссами а и b равна

_

s=J VI + [/(ж)]² dx.

а

В случае параметрич. ур-ий

«-j/W+W"·

С

Пример. Для циклоиды дифференциал дуги

ds=2а sin ~ dt.

Длина одной ветви

^2π t г π^2π

s=2α J sin 2 di=— 4α pos ‘-J=8α.

Длина дуги в полярных координатах дается формулой:

β _

s=J Vdr² + r²d<p².

а

Объем тела вращения. Кривая y=f(х) вращается около оси абсцисс; требуется определить объём, ограниченный поверхностью вращения и плоскостями х=а, х=b. Разбивая объём на элементарные, которые вычисляем по избытку и недостатку как круглые цилиндры, и переходя к пределу, найдем:

V=π J у² dx=π j [f (ж)]² dx.

a a

Вообще, если у тела любой формы площади сечений, перпендикулярных к оси абсцисс, известны в ф-ии ж, например X, то объём выразится следующим образом: ь

V=jXdx.

Пример. Найти объём эллипсоида г _Ь, -Г _сг

При данном ж имеем в сечении эллипс

У³ ,____2? _ I

Ь² (а² - х^г)

с² (а² - х²)

с полуосями ^ V а² — ж² и | Vа² — х² и с площадью (а² — ж²). Искомый объём

Л а

V=~~ J (а² — ж²) dж=2 π abc.

—а

Поверхность тела вращения S выражается интегралом:

5 δ__

S=2π j у ds=2л J f{x) Vl -j- [/(ж)]² dx.

a a

Центр тяжести. В механике координаты ц. т. системы точек Р_г с массой т_х и координатами (x_lt Уг),Р₂(т₂,ж₂,2/₂). даются формулами:

_ Σι»,·Xj _ s mm Σιη_{ ’ У Σ-mi

Если масса распределена непрерывно, мы совершаем переход к пределу и вместо сумм получаем интегралы.

1) Центр тяжести дуги. Принимая массу единицы длины равной 1, будем иметь:

j xds

— а

X =-.

δ

fds

У =

b

S у ^ds

г

b

s *

2) Центр тяжести плоской фигуры. Считаем массу единицы площади равной 1. Берем криволинейную трапецию, .разбиваем ее на полоски и заменяем их прямоугольниками. Замечая, что площадь элементарного прямоугольника равна укх, а ц. т. находится на половине высоты, получаем, переходя к пределу:

1 ^δ

2 f V³dx

— ^ύ а х=--; у =

ь

f ху dx

f V dx

Ь

f у dx

Пример. Найти ц. т. полукруга у=+ Va² — х².

Очевидно

- ~а х=0; у=(а² — ж²) dx: ^ л а²=^

Момент инерции плоской фигуры. Момент инерции относительно оси абсцисс конечной системы точек 1_Х имеет выражение: Ι_χ=Σ т₍ yl а относительно оси ординат: l_y=im_ix. Для криволинейной трапеции получим: I_x=j х²у dx. Для вычисления 1_у

а заметим, что момент инерции элементарного прямоугольника равен ~Дж, откуда

^Iy=Uv^3dx·

Интеграл как функция параметра. Пусть подинтегральная ф-ия зависит, кроме ж, еще от параметра ί. Интеграл

J/(ж, t)dx не зависит, как мы видели, от ж,

а но является ф-ией параметра ί. Применяя определение производной, получаем ф-лу:

£ J /(^ж> О ^,1х=17Л /(^ж> О ^dx.

дающую правило дифференцирования определенного интеграла по параметру. Если пределы интегрирования а и 6 тоже зависят от ί, формула примет вид:

ь

/(*> t)dx= J ~/(ж, t)dx +

+ f(b,t)%-Ka, i)$.

Определенный интеграл как ф-ию параметра можно также интегрировать по параметру. В случае постоянных пределов имеем:

β β

S {S η^χ> t)dx } dt=J’ -[ J/(ж, t)dt j- dx,

a O & a.

t. e. порядок интегрирования по переменному и по параметру можно менять. В случае бесконечных пределов интеграции это правило справедливо только в случае равномерной сходимости интеграла J (ж, i) dx это а значит: для сколь угодно малого ε можно найти достаточно большое Ь так, что

f f(x, ί) dx ь

< ε

для всех значений ί в пределах интеграции.

Приближенное вычисление интегралсв (механические квадратур ы)—см. Вычисления приближенные.

Интегрирование рядов—см. Ряды.

Двойные интегралы. Дана непрерывная ф-ия от двух переменных (ж, у). Уравнение z — f(x, у) геометрически представит поверхность. Требуется определить объём,

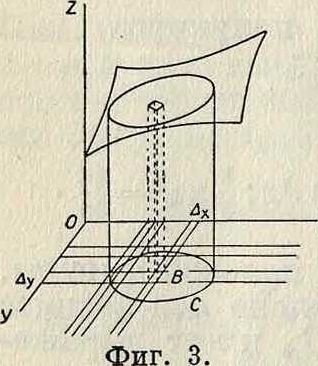
ограниченный этой поверхностью, плоскостью XY и цилиндрич. поверхностью, направляющая которой—замкнутая кривая С на плоскости XY. Разбиваем плоскость XY прямыми, параллельными осям координат, на маленькие прямоугольные площадки Ах -Ау и через линии деления проводим плоскости, параллельные OZ (фигура 3). Отберем те прямоугольники, которые имеют общие точки с площадью В, ограниченной кривою С;

в каждом прямоугольнике берем соответствующее значение fix, у), например /(ж, ?/*), и составляем сумму: Σ /(ж_г, у_к) Ах Ау. Предел этой суммы, когда Ах и Ау стремятся к нулю, запишется как JJ /(ж, y)dxdy (двойной ин-(В)

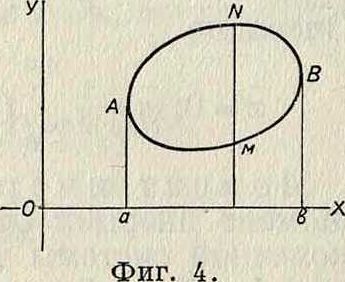
теграл, распространенный на область В). Геометрически он представит искомыйобъём. Для вычисления двойного интеграла производим под знаком Σ суммирование сначала по у, потом по ж (или наоборот). Предположим, что кривая пересекается параллелями к оси ординат в двух точках. При переходе к пределу придется сначала интегрировать по у от М до N, затем по ж от а до Ь (фигура 4). Для аналитическ. выражения предположим, что дуга АМВ дана ур-ием ν=ψ₁{χ), дуга AN В—ур-ием у=^гр^.{х).

Тогда

b <Р_г(х)

fix, У) dx dy=J dx f fix, у) dy.

(В) a <p,(x)

В частности, если В—прямоугольник, ограниченный прямыми: ж=а; x=b; у=с; y=d, получим:

ь d

J S /(ж, у)dxdy=f dx f f(x, у) dy

(В) a c

(пределы по у также постоянны).

Замена переменных в двойном интеграле. Пусть надо ввести такие переменные и я V, что ж=9>(м, v), y=y>iu,v). Тогда имеем ф-лу:

j’ (ж, У) dxdy=JJ f W iu, v), y>iu, υ)] J D | dudv,

(в) (W)

где Ώ есть определитель Якоби:

δφ δφ

D =

ди δυ δψ δψ ди δυ

a W—область плоскости (u,v), в которую переходит область В. В частности, при переходе к полярным координатам x=r cos <р, y=r sin <р, имеем:

дх дх дг δφ ду ду дг δφ

следовательно,

Jjfix, у) dxdy=JJfir COS φ, r sin φ) r dr d φ. Пример. Интеграл Пуассона

+»

Имеем

+“

dx.

+» ₊«

I²=f е~^х‘ dx f е~у dy=J’ J e~^x dx dy

двойной интеграл, распространенный на всю площадь. Переходим к полярным координатам:

2π со

Р=JJ e~^r‘rdr d<p=J dip J e~^rr dr=π,

0 0

следовательно, I=Υπ~.

Приложения двойного интеграла. Кроме вычисления объёмов, двойной интеграл служит для вычисления кривых поверхностей. Здесь имеем ф-лу: площадь поверхности z=f(x, у), ограниченной цилиндром с направляющей С:

где

S= JJVl + fl+fsdxdy,

(.В)

, э .9

I^х дх ’ У ду

Координаты ц. т. площади В выразятся так:

ж =

SS Xdxdy ffydxdy

(В) -₌ (В)-----

в в

Момент инерции площади В относительно оси ординат:

I=//ж³ dx dy.

(в)

Тройной интеграл. Дается функция трех переменных /(ж, у, z) и область В, ограниченная поверхностью S. Пространство разбивается плоскостями, параллельными координатным, на малые параллелепипеды и составляется сумма произведений значений ф-ии внутри параллелепипеда на его объём:

2 f(x_t, у_к, 2₍) Да: Δу Дя ;

знак суммы распространяется на параллелепипеды, имеющие общие точки с В. Предел этой суммы есть тройной интеграл: JJJ (ж, у, z) dx dy dz. Его вычисление свода дится к последовательному интегрированию сначала по х, затем по у, наконец — по z. Тройной интеграл применяется к вычислению ц. т. и моментов инерции объёмов, также в гидромеханике, теории потенциала и т.д.

Криволинейные интегралы. Пусть дана функция /(ж, у) и на плоскости XY кривая С: χ=ψ(1), y=y>(t). Под криволинейным интегралом по кривой С от точки Α(ί₀) до точки Β(ίχ), т. e. JP(x, у) dx, понимается (С) i,

интеграл J Р [φ (ί) ψ(ί)] ψ (t) d t. Этот интеграл

to

зависит от направления кривой: интеграл от В до А равен интегралу от А до В, взятому с обратным знаком. Аналогично определяется Q(x,y) dy и наиболее общий криволинейный интеграл

J Р dx+ Q dy.

(С)

Если, в частности, кривая С замкнутая и ограничивает область В, то существует следующая связь криволинейного интеграла с двойным (ф-ла Грина):

jP dx + Q dy=J (If - Щ)йх dy.

(C) (B)

Подобно криволинейному интегралу определяется интеграл по поверхности. Имеем ф-ию от 3 переменных В(х, у, z) и поверхность S; тогда

JJ-R (ж, y,z) dxdy=JjR(x, у, z) cosy da,

(S) да где ж, у, г выражены в функции переменных и, V (смотрите Дифференциальная геометрия), da—элемент площади поверхности, γ—угол нормали с осью ΟΖ. Наиболее общий интеграл по поверхности

JJ Р dy dz + Qdzdx + Rdx dy=

(S)

= J J (P cosa + Q cos/ϊ + R cosy) da,

да где a и β—углы нормали с осями ОХ и ΟΥ. Если поверхность S замкнута и ограничивает объём V, то этот интеграл равен

JXf(sf+! +™)dxdydz (ф-ла Остро-(V)

г р а д с ко г о-Гр и н а). Пусть в пространстве дан криволинейный интеграл J’ Р dx +

(D

+ Q dy -f R dz. Если кривая L замкнутая, то этот интеграл можно выразить через двойной интеграл по части произвольной поверхности Σ, ограниченной кривою L; а именно, имеет место равенство (формула Стокса):

Pdx + Qdy + R dz=— //(ff — Щ) dy dz +

(.L) (.Σ)

+ {Ш~f) ^dzdx+{^dd^Py-^dai) ^dxdy-

Эти формулы имеют большое применение в механике; их более простую запись и геометрическую интерпретацию дает векторное исчисление (смотрите).

Лит.: Гурса Э., Курс матсматич. анализа,

пер. с франц., т. 1, М., 1911; Филипс Г., Интегральное исчисление, пер. с англ., М.—Л., 1927; Г р е н в и л ь В., Элементы диффер. и интегр. исчисления, пер. с англ., ч. 2, 6 изд., М.—Л., 1928; Б и-б е р б а х Л., Дифференциальное и интегральное исчисление, пер. с нем., ч. 2—Интегральное исчисление, М., 1924. В. Степанов.