 > Техника, страница 49 > Интегральные уравнения
> Техника, страница 49 > Интегральные уравнения
Интегральные уравнения
Интегральные уравнения, ур-ия, в к-рых искомая ф-ия входит под знаком интеграла. Первое И. у. получено и решено Абелем, исследовавшим механич. задачу: определить вид кривой, по которой движется маятник, если время колебания Т есть данная ф-ия наибольшей высоты. Представляя ур-ие искомой кривой в виде в=Ф (z) (s—длина дуги, z—высота), мы для ф-ии φ (ζ)=Φ(ζ) получаем И. у. Абеля:
/WfW, (1)
J У h-z
о где f(h)= j/^l T (g—ускорение силы тяжести).Ур-ие (1) имеет решение:
ш.
О
Общая теория И. у. создана трудами Воль-терра, Фредгольма, Гильберта и др.
Уравнения Вольтерра 1-го рода являются обобщением ур-ия Абеля; общий вид такого ур-ия:
/(ж)=J* K(x,s)<p(s) ds,
(2)
где и К—данные ф-ии, ψ—искомая ф-ия. Ф-ия К называется ядром И. у.; в случае (1)ядро равно -7— ; оно бесконечно при
Ух - s
x=s; этот случай в общей теории представит некоторые затруднения. Если же ядро уравнения (2) непрерывно и дифференцируемо, то, дифференцируя ур-ие (2) цо ж, получаем:
X
/(ж)=К(х, χ)φ(χ) + Кх (ж, s) (pis) ds ;
О
предполагая К(х, х)фО, можем разделить обе части ур-ия на него; применяя новые обозначения, получим ур-ие вида:
/(ж)=φ (ж) + J Щх, s) <f(s) ds, (3)
а уравнение Вольтерра 2-г о рода (К и /—известны, φ—ищется). Для решения уравнения (3) вводим параметр Я и составляем уравнение вида:
ψ(β)=Я f К (ж, s) <p(s) ds + fix). (3)
О
Ищем решение в виде степенного ряда:
<р(х)=<Ро(х) + λ<Ρι (ж) + AVa (ж) +
+ ·. > + ληφη (ж) +. (4)
Подставляя выражение (4) в ур-ие (3) и приравнивая коэффициенты при различных степенях Я, находим:
X
Ψο (ж)=(ж); (ж)=К (ж, s) ?>0(s) ds ;
а х
φ2(χ)=J К (ж, s) (s) ds ,.,
а
X
<pjx)=f к (ж, s) 9Vi (s)ds ·
a
Ряд (4) сходится при всех значениях Я; при А=1 имеем решение ур-ия (3). Решение (4) можно представить одной формулой. Назовем
J К (ж, ί) К (ί, у) dt=К™ (ж, у),
У
/-К<!) (ж, ί) К (ί, у) dt=Кт (х,у),.,
У
Sк^ х, t)K(t, y)dt - г<к,(ж, »),.
У
последовательными повторениями ядра К. Составим ф-ию:
Г (ж, у, λ)=Κ (ж, 2/) + яд(!> (ж, 2/) +
+. +Я“-1^<И)(ж,2/)Н-.„ (5)
т.н. резольвенту ур-ия (3)· Тогда решение (4) запишется так:
<Р(х)=/(ж) + Р (ж, s; Я) /(s) ds.
а
Наряду с И. у. Вольтерра в приложениях встречаются иптегр о-д ифференци-альные ур-ия, где вместе с искомой ф-ией ψ входят также ее производные (как под знаком интеграла, так и вне его). Обыкновенно рассматриваются интегро-дифференциаль-ные ур-ия линейные (в которых искомая ф-ия и ее производные входят линейно).
Другой важный тип И. у.—у равнение Фредгольма. Общий вид" ур-ия Фредгольма (2-го рода):
<р(х)=К. (ж, s) φ(ε) ds + fix).
a
Здесь опять К (ядро) и f—данные ф-ии, φ—
искомая ф-ия; отличие от ур-ия Вольтерра в том, что оба предела интеграции а и & постоянны. Мы по прежнему рассматриваем более общее уравнение
h
<р(ж)=Я f K(x,s) <p(s) ds + fix). (6)
a
И здесь можно искать разложение в форме (4), причем будем иметь:
ь
<Ро(х)=/(ж); <Ρι(Ж)=f к (ж, s) ¥>„(s) ds,
а
b
<Рг{ж)=/Щх, s) 9>i(s) ds,.,
а
b
φη(χ)=К (ж, s) φη-! (s) ds.
a
Повторения ядра для И. у. Фредгольма определятся так:
к (ж, s) К is, у) dy=Кт (ж, у),
а
J (ж, s) JC(s, г/) dy=I03)ix, ?/),···,
а
S #(,M> (ж, S) К (S, у) dy=Д<И)(ж, г/) ,.
а
С этими новыми выражениями повторений резольвента Г (ж, у; Я) выразится той же ф-лой (5), а решения ур-ия (6)—
φ(χ)=fix) + Я J Г (ж, s; Я) /(s) ds. (7)
а
Но в И. у. Фредгольма встречается особенность: ряд (5) сходится только для значений Я, достаточно малых по модулю. Фредгольму удалось дать выражение резольвенты для всех значений Я в виде частного двух ф-ий, целых относительно Я:
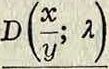
Для значений Я, не обращающих в нуль знаменатель, решение ур-ия (6) дается ф-лой (7); если же Б(Я)=0 для Я=с, то уравнение (6) при произвольной ф-ии fix) вообще не имеет решения; зато имеет решение (одно или несколько), отличное от нуля, соответствующее однородное ур-ие:
9>(ж)=с J Kix,s)(p (s) ds. (8)
а
Эти значения с называются фундаментальными чи, а соответствующие им решения ур-ия (8)—фундаиен-тальными функциями. Особенно интересный класс представляют И. у. с симметричным ядром, то есть такие, где Щх, у)=Щу, ж). Здесь мы имеем следующие свойства: всякое симметричное ядро обладает хоть одним фундаментальным числом (собственным значением); все собственные значения Ях, Я2,. действительны; соответствующие им фундаментальные (собственные) ф-ии ¥>х(ж), <р2(ж),. можно выбрать так, что они образуют ортогональную систему в интервале (а,Ь), то есть ь
j <Pi(x) <Pk (ж) йж=0 {гфк);
а такова, наприм., система 1, cos ж, cos 2х,., sin®, sin 2х,. в интервале (0; 2π).
Так как собственные функции определяются с точностью до постоянного множителя, то их можно предполагать нормированными, то есть х=1.
а
Если симметричное ядро имеет только конечное число собственных значений, а собственные функции приведены к ортогональной и нормальной системе, то имеет место равенство:
Щх, у) - *<&!№. + +. (9)
(нек-рые λ{ м. б. равны между собою). Ра-вбнство (9) имеет место и для случая беско-нечного множества чисел Аг при некоторых ограничениях, наложенных на ядро. При этих условиях резольвента имеет вид:
Пх,«ΟΙ-Στί5 ’
Связь И. у. с дифференциальными уравнениями. Многие задачи математической физики (например колебание неоднородной струны с закрепленными концами) приводятся к решению дифференциального ур-ия 2-го порядка:
([риУ — qu + Aw=0, (10)
с граничными условиями: и(а)=0, и(b)=0; (р, q—ф-ии от х, р>0; А—неизвестная постоянная). Ур-ие (Ю) приводится к И. у. типа Фредгольма с симметричным ядром. Для этого строим функцию Грина G(®,£). Это есть решение дифференциального ур-ия (риУ— qu=0, удовлетворяющее граничным условиям, непрерывное между а и b; но
1-я производная по х имеет в точке f (а < f < Ь) разрыв непрерывности:
х=£+о
pG(x, ί)Ί =__1_ _
L Эх J Ρ(ί)
χ=ξ- о
Функция Грина удовлетворяет условию симметрии: G(x, £)=G(£, ж), и всякое решение ур-ия (10) удовлетворяет однородному И. у. (2-го рода):
м(ж)=A f G(x, ξ) м(|) d{.
а
На основании изложенной теории, это И. у. имеет отличные от нуля решения лишь тогда, когда А равно одному из собственных значений Af; соответственные решения и(х)=<р£х) будут собственные ф-ии; они образуют ортогональную систему. Решение неоднородного дифференциального ур-ия (риУ — qu + Aw=ψ(χ)
сводится к интегральному уравнению неоднородному:
и(х)=A J G(x, ξ) w(f) άξ + g(x),
a
Ь
где д(х)-- G(x, ξ) ψ (ξ) άξ. Теория И. у. а легко обобщается на случай, когда искомая функция зависит от нескольких аргументов, например, на уравнения Фредгольма: ь
<Р(х,У)=S S Κ(χ,ν,ξ,η) φ(ξ,η) άξ άη + f(x,у).
а а
Эти ур-ия могут служить для решения проблемы Дирихле и Неймана (смотрите Потенциал) или, например, задачи о плотности электричества на проводнике данной формы (задача Робена) и т. д.
Лит.: Белоновекий П. Д., Интегральные уравнения и их роль в математическ. физике, Вятка, 1928,- Courant R. u. Hilbert D., Metboden d. mathemat. Physik, В. 1, В., 1924; К n e s e r A., Integralgleichungen u. ihre Anwendung auf die mathemat. Physik, 2 Aufl., Brschw., 1922; G о и r s a t E., Cours d’Analyse, 3 dd., t. 3, P., 1922. В. Степанов.