> Техника, страница 49 > Интегрирующие приборы

Интегрирующие приборы

Интегрирующие приборы, приборы, осуществляющие чисто механич. путем интегрирование некоторой заданной обычно графически ф-ии. Двум задачам интегрального исчисления—нахождению определенного интеграла и нахождению интегральной кривой—соответствуют две группы интегрирующих приборов. К первой группе относятся: 1) планиметры, то есть приборы, служащие для нахождения площади, ограниченной заданным контуром; 2) интеграто-р ы, дающие значения определенных инте-ь ь градов J /(ж) dx, J f ж) dx, f fix) dx для ф-ии

a a a

f(x), заданной графически, иЗ) гармонические анализаторы (смотрите Гармонический анализ). Ко второй группе относятся интеграфы, то есть приборы, вычерчивающие по заданному ур-ию /(ж, у, ,.,=⁰

интегральную кривую y=fix) и, в простейшем случае, по уравнению ^=Fix) — кривую у=f Fix) dx.

В основе конструкции большинства наиболее употребительных планиметров и интеграторов лежат следующие соображения. Пусть отрезок прямой В А скользит по плоскости; при своем движении он зачерчивает

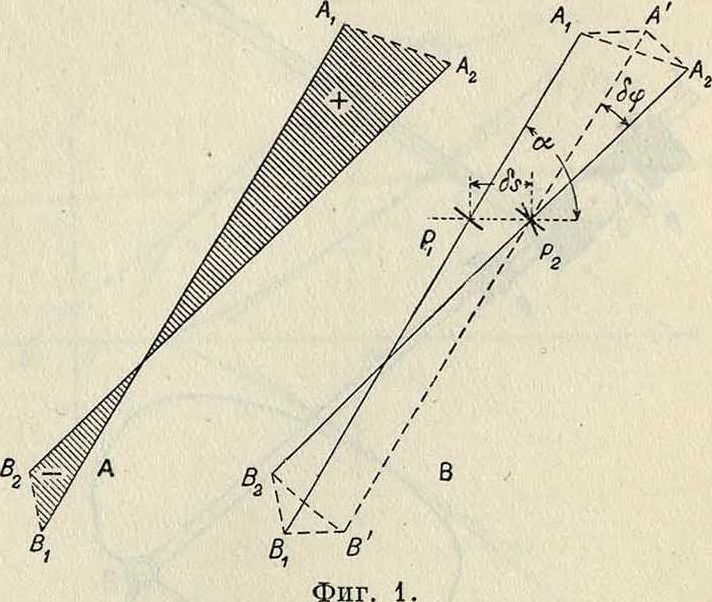
нек-рую площадь; условимся считать ее положительной, если для наблюдателя, смотрящего по направлению стрелки, она остается влево, и отрицательной, если она остается вправо от движущегося отрезка. Тогда вся площадь, зачерченная отрезком при перемещении его из положения А₁В₁ в Д₂В₂, выразится в виде суммы положительных и отрицательных площадей (фигура 1, А). Как известно, элементарное перемещение в плоскости м. б. разложено на поступательное перемещение, определяемое перемещением произвольно выбранной точки Р, и на вращение вокруг этой точки. Вообразим на нашем отрезке (фигура 1, В) в точке Р_х колесико, имеющее своей осью отрезок ВА и при его

движении катящееся по плоскости. Из двух указанных выше элементарных движений только поступательное движение вызовет

- δs Sin α

вращение колесика на угол οω=——, где

<5s—перемещение точки Р_х, а—угол между этим перемещением и направлением отрезка и г—радиус колесика. Элементарная же площадь, зачерченная при этом перемещении,

будет равна I дз sin а+

здесь I—длина отрезка, —=и δφ—эле ментарный угол поворота отрезка. Последнее выражение можно представить в виде 1г δω + Ιξ δφ, где ξ=~ I —расстояние Ρχ

от середины отрезка. Обведем концом Αχ

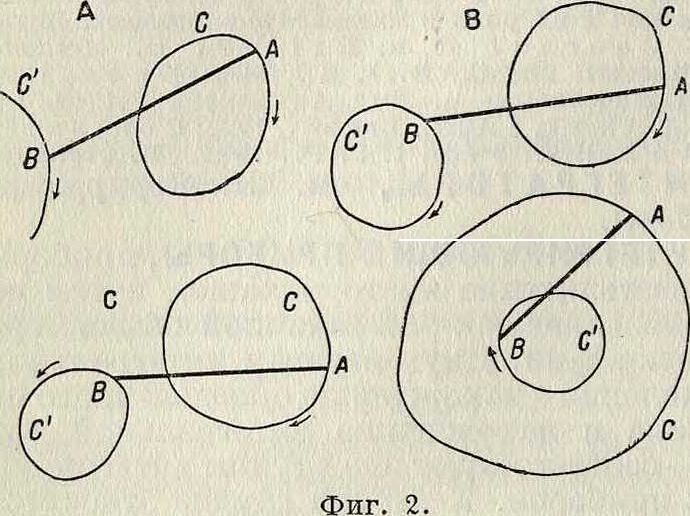
отрезка контур, ограничивающий площадь, подлежащую определению, т.о.,чтобы после этого отрезок В_гА_х вернулся в свое исходное положение. Зачерченная площадь будет тогда равна 2 1г δω -)- 2 Ιξ δφ=Ιτω -f Ιξφ, где со—угол поворота колесика вокруг его оси, а ψ—угол поворота отрезка. Так как отрезок возвращается в свое исходное положение, то угол ψ=0 (фигура 2, А, В, С) или φ =2π (фигура 2, D). Обозначая через (С) и (С) площади, ограниченные контурами О и О, получим для четырех случаев, изображенных на фигуре 2, соответственно:

(С)=Ινω; (С) - (С)=Irw,

(С) + (С)=Ινω; (С) - (СО=Βω + 2πΙξ.

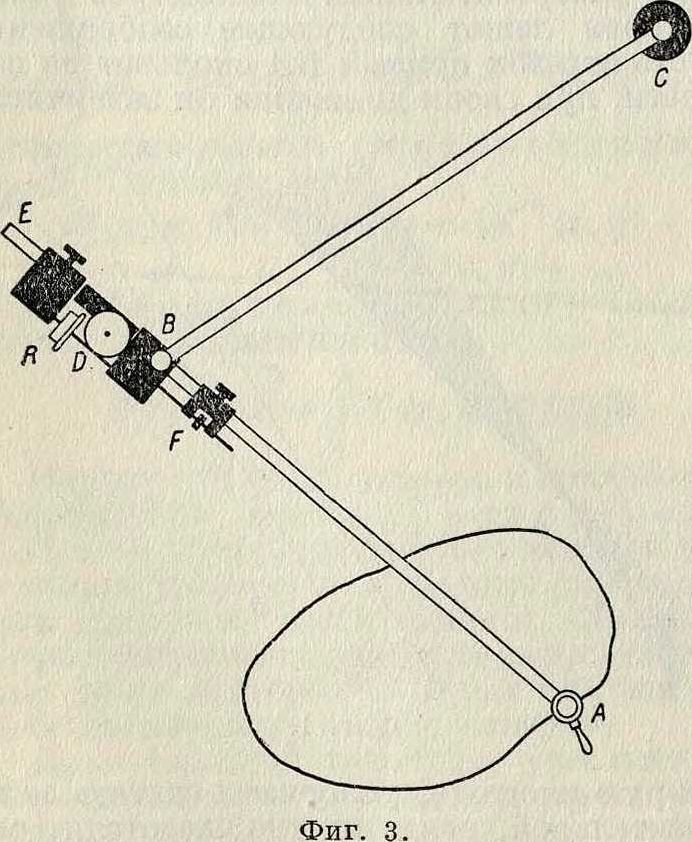
Полярный планиметр Амслера (фигура 3) есть непосредственное применение изложенной теории. В нем точка В ведется с

по окружности круга с центром в С, и, в зависимости от размеров обмериваемой площади и расположения прибора, мы имеем или случай «А» или случай «D» (фигура 2). Целое число оборотов колесика В отсчитывается на циферблате D, доли же оборота— на барабане, укрепленном на колесике. Длина 1=ВА может изменяться передвижением стержня АЕ. Для малых передвижений служит микрометрический винт F. На планиметре, представленном на фигуре 3, ось колесика не совпадает с линией АВ, но нетрудно видеть, что при параллельности линии АВ отсчет по колесику от этого не изменится, если за точку Р считать пересечение АВ с плоскостью колесика. При непа-раллельности появляется систематическая с

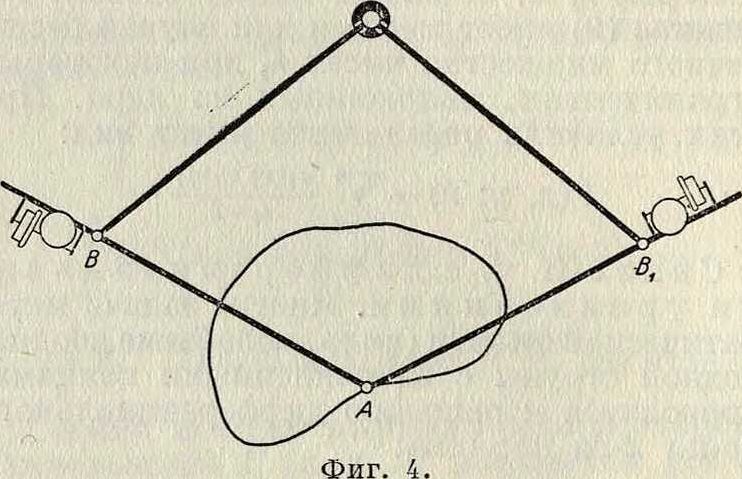
ошибка прибора, для исключения которой рекомендуется обвести контур дважды при двух различных положениях прибора (фигура4) и брать полусумму отсчетов. Описанная конструкция представляет два неудобства:

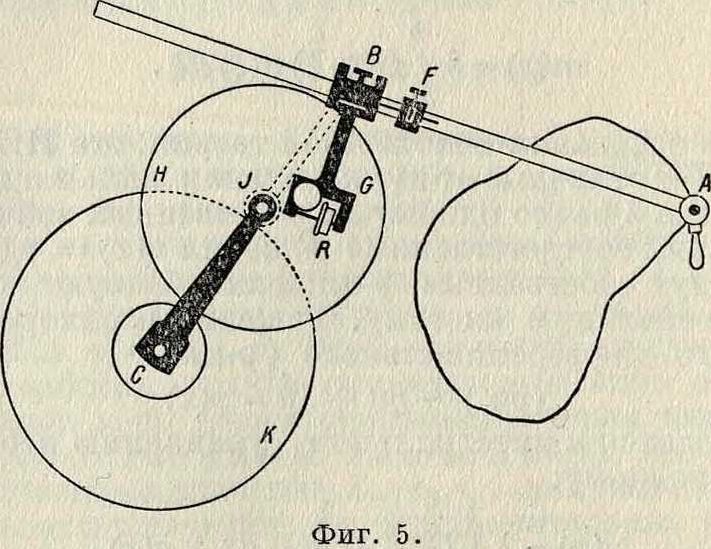
1) катание колесика непосредственно по чертежу не обеспечивает правильности его показания и 2) незначительность числа оборотов колесика увеличивает относительную ошибку отсчета. Оба недостатка устраняются в дисковом планиметре (фигура 5), где колесико R, укрепленное на вилке G, катится по диску Я; последний сцепляется шестерней J с неподвижной шайбой К. Вращение АЕ вокруг В не вызывает вращения колесика, так как плоскость обода проходит через ось В, вращение же ВС вокруг С, дающее АЕ поступательное движение, сообщая вращение диску, вызывает вращение колесика R. Это вращение колесика находится в постоянном отношении к тому вращению, которое имело бы колесико, катясь по неподвижной плоскости.

Типом, переходным к приборам, которые мы называем интеграторами, являются планиметры Коради, где круговое движение точки В заменено прямолинейным

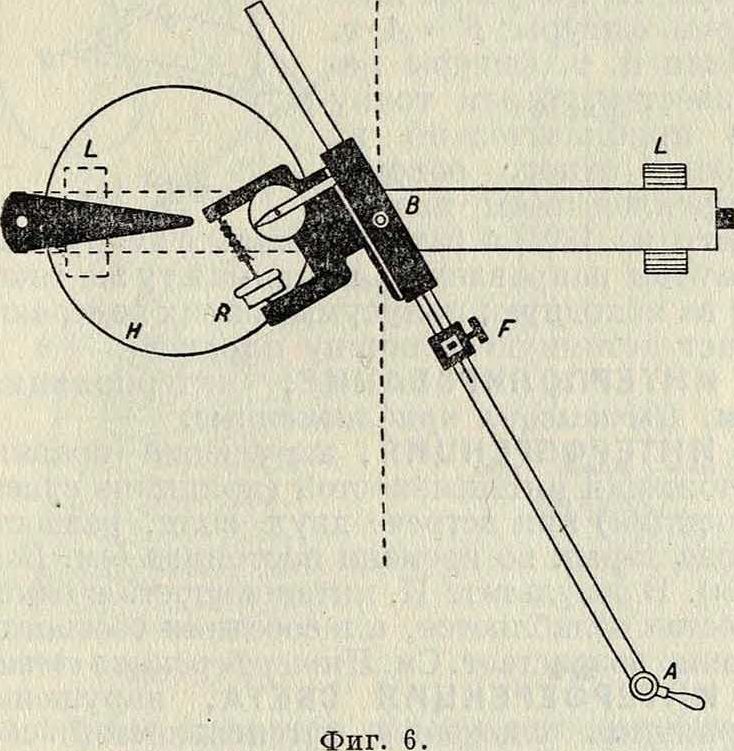
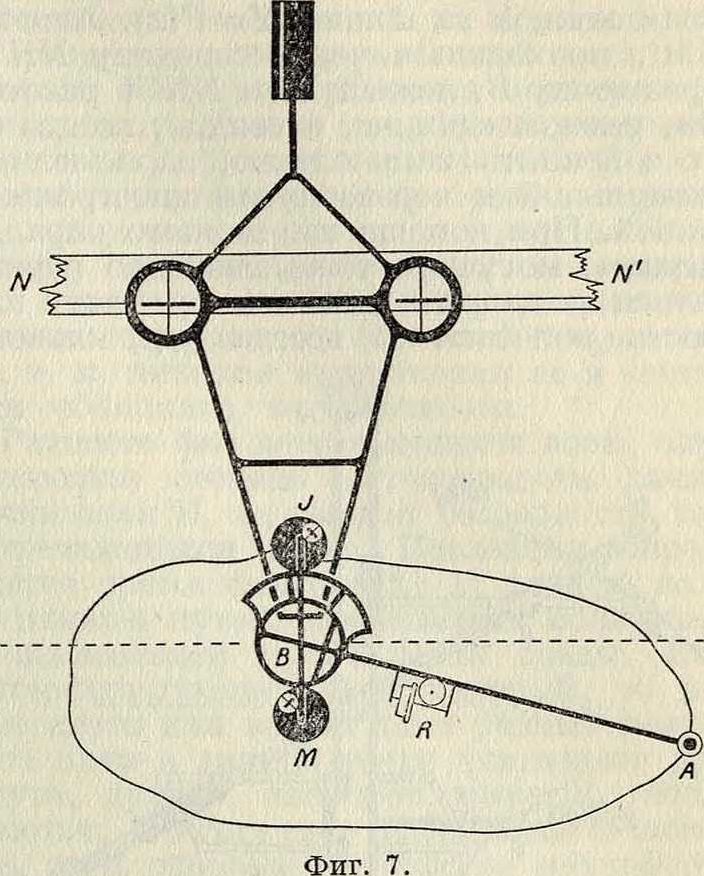
при помощи цилиндрич. роликов L (фигура 6). Колесико R катится по диску Я, угол поворота которого пропорционален поступательному перемещению прибора, а следовательно, и стержня АВ. Поворот АВ вокруг точки В не сообщает вращения колесику; в равной мере оно не получает вращения, когда АВ имеет направление поступательного движения прибора. Интегратор Амслера (фигура 7) есть тот же планиметр, но с прямолинейным движением точки В. Интерес представляют добавочные устройства, по-

ь зволяющие находить интегралы вида f у² йх а

b

и j‘y³dx, к которым приводится вычисле-

а ние статических моментов и моментов инер-ции плоских фигур. Ведущая линейка ЯЯ обеспечивает прямолинейное движение точки В. Отсчет по колесику R дает площадь обмериваемой фигуры. Со стержнем АВ неизменно связано двойное зубчатое колесо с радиусами Зг и 2г, сцепляющееся с двумя зубчатыми колесами М и J радиусов г, на которых имеются колесики, подобные коле сику R. Можно показать, что отсчет по этим колесикам дает статический момент и момент инерции. Фирма Коради изготовляет

также интеграторы Hele-Shaw, построенные по принципу, близкому к принципу, лежащему в основе анализатора Генричи (смотрите Гармонический анализ).

Интеграф Абданк-Абакановича есть наиболее известный прибор этого типа. Его устройство основано на свойстве колесика с острым краем при катании по плоскости двигаться так, что бесконечно малое перемещение его центра лежит в плоскости колесика. Пусть Y=F(x)—заданная кривая, а у=J F(x)dx=0(x)— соответствующая интегральная кривая. Тогда, очевидно, угловой коэффициент ~ интегральной кривой равен соответствующей ординате кривой Y=F(x). Отсюда видно (фигура 8), что, отложив NQ=1 и проведя QM, получим

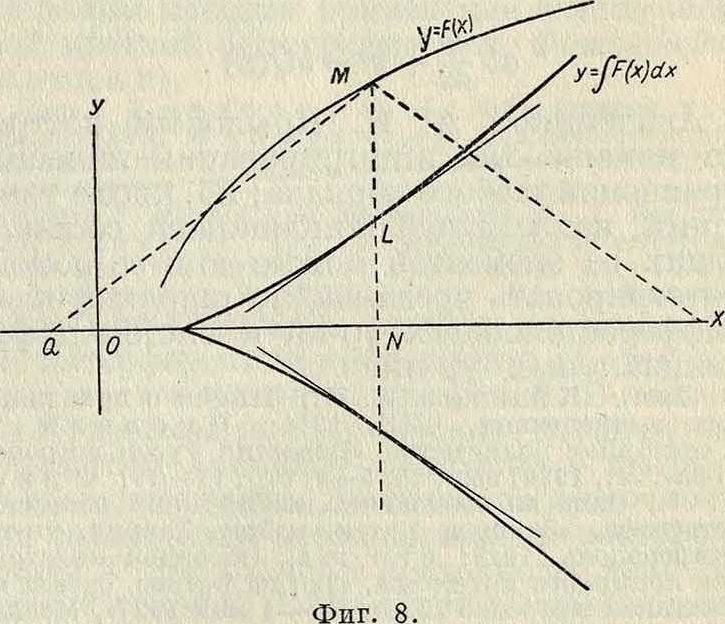
направление касательной к интегральной кривой в точке L. Перегнув чертеж около оси абсцисс, получим другое расположение интегральной кривой, соответствующее тому, которое на самом деле дает интеграф.

Устройство прибора видно из чертежа (фигура 9). Точка А, имея два движения—по оси абсцисс вместе с линейкой NN и по оси ординат вместе с тележкой S,—следит своим концом за кривой Y=F(x). Линейка ММ, проходящая через середину NN и через точку В, лежащую от NN в расстоянии, равном единице, очевидно, всегда будет сохранять направление, параллельное касательной к перевернутой интегральной кривой. При помощи шарнирного паралле-лограма, могущего тоже свободно перемещаться в направлении оси ординат, плоскость колесика В всегда удерживается

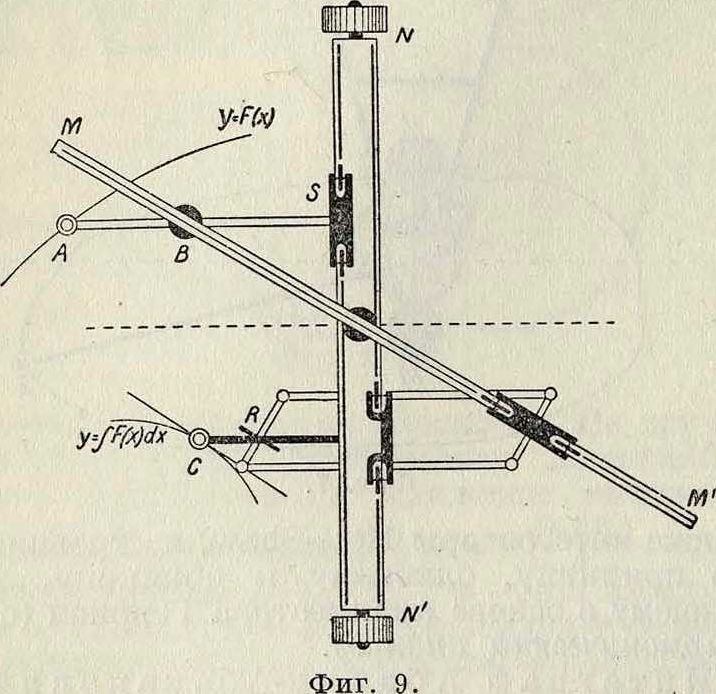
параллельною линейке ММ, то есть параллельною той же касательной. Теперь ясно, что при обводе заданной кривой точкою А колесико R будет прочерчивать интегральную кривую (перевернутую); ту же кривую, но смещенную влево, вычертит карандаш, укрепленный в С.

Дальнейшим развитием этого прибора являются интеграфы для дифференциальных ур-ий. Е. Паскаль построил ряд приборов, среди которых имеются интеграфы для ур-ий:

« Ш + У ⁼ Q(®)

И

abf_x + y*=bQ(x).

Академиком А. Н. Крыловым построена машина для интегрирования линейных уравнений любого порядка; но, кроме таких ур-ий, надлежащей комбинацией составляющих ее элементов можно при ее помощи интегрировать чрезвычайно широкий класс дифференциальных ур-ий и систем дифференциальных ур-ий.

Лит.: Крылов А. Н., Лекции о приближенных вычислениях, СПБ, 1911; Я ков кин А., О секторном планиметре, «Известия Русск. астроном, об-ва», Л., 1924, вып. 25, 5—9, стр. 17—19; Франк M. Л., Одна из возможных конструкций полярного интеграфа, «Записки Матем. кабин. Таврич. ун-та», Симферополь, 1919; его же, Об одной конструкции полярного интеграфа, «Труды Всерос. съезда математиков в Москве 27 апреля—4 мая 1927», Москва, 1928, стр. 189—190; Horsburgh E. М., Modern Instruments and Methods of Calculation, A Handbook of the Napier Tercentenary Exhibition, Edinburgh, 1914; Galle A., Neue Integraphen. «Zeitschrift fiir angew. Mathem. und Mechanik», Berlin, 1922, B. 2, p. 458—466; Morin H., Les appareils d’intigra-tion, Paris, 1913; Pascal E., I miel integraphi, Napoli, 1914. К. Меликов.

Интересной системой планиметра является планиметр П р и т ц а, замечательный своей чрезвычайно простой конструкцией. Он состоит из изогнутого стального прутка а (фигура 10), снабженного на одном конце острием б, а на другом—закругленным лезвием в, плоскость ребра которого проходит через острие б.

Расстояние бв=А является постоянной прибора. Для определения площади какой-либо фигуры В помещают острие планиметра в центре тяжести фигуры О (фигура 11), затем отмечают положение В лезвия в («топорика») на бумаге и обводят контур, как обычно, возвращаясь опять в исходную точку О. В это время топорик вычертит на бумаге сложную кривую Вввв"В". Измеряя расстояние е между начальным и конечным по ложениями топорика и помножая его на постоянную прибора А, получаем площадь фигуры: F — А е.

Если ц. т. фигуры неизвестен, берем точку О приблизительно и, после одного обвода, перекладываем планиметр на 180°, а затем обводим фигуру в обратном направлении, принимая ту же точку О за исходную; полусумма обоих измерений даст истинную величину площади.