Испарение

Испарение, переход вещества из жидкого состояния в газообразное (парообразное). И. происходит со всякой свободной поверхности жидкости. Механизм И. с точки зрения молекулярно-кинетической теории заключается в следующем. Молекулы жидкости, находящиеся вблизи от ее поверхности и обладающие в данный момент большой скоростью в направлении, образующем достаточно большой угол с поверхностью, вылетают в пространство над жидкостью, освобождаясь от притяжения остальных молекул жидкости; таким образом они становятся свободными молекулами пара. На преодоление сил сцепления жидкости и сопротивления внешнего давления для каждой испаряющейся молекулы требуется затрата энергии (тепловой).

Количество тепла ρ, затрачиваемого на И. при данной ί° одной весовой единицы жидкости, называется скрытой тепло-

той И.: e=Qi+Q_e, ^гД^е Si — внутренняя скрытая теплота И., расходуемая на внутреннюю работу разъединения молекул, а о_е — внешняя скрытая теплота испарения, затрачиваемая на внешнюю работу расширения вещества от удельного объёма s жидкости до удельного объёма а пара. Теплота испарения тд, отнесенная к граммолекуле жидкости, называется молекулярной теплотой И. Соответственно употребляются то и тд_е. В технике полной теплотой И. Я называется количество тепла в Cal, затрачиваемое на 1 килограмм жидкости для нагревания от 0° до данной темп-ры ί и на превращение ее при этой темп-ре в пар:

h=q^JrQ=q-|-£?г+ (?,>!

где q— количество тепла, затрачиваемое на нагревание жидкости. Теплотой пара называется сумма

<7 + ί?ί=J" С dt + Qi, о где С — теплоемкость жидкости. Теплота пара определяет избыток энергии пара над

Значения удельных теплот испарения для воды.

i°	Д авление в килограммах/см²	паров р в миллиметров Hg	λ	6	6е	ei
0	0,00622	4,575	595.0	595,0	30,1	564,9
25	0,0323	23,76	606 6	581.6	32.8	548,8
50	0,1258	92.53	618,0	568 0	35.5	532 5
75	0,3929	288,99	629,0	554,0	38.1	515.9
100	1.0333	760,00	639,4	539.4	40,5	498.9
125	2.3662	1740.42	648.8	523.5	42.7	480,8
150	4,8517	3568,61	657.0	506 0	44.6	461 4
175	9,0937	6688.74	663.5	486 5	46,1	440.4
200	15,854	11661,2	667.7	464.2	46,9	417.3
225	26,003	19126,2	669,0	438.4	47.1	391.3
250	40.547	2382 <,8	666,4	408.1	46,3	361 8
275	60.625	44592,0	659,4	372.5	44 3	328.2
300	87.63.	64455,2	646,8	330 2	40.8	289.4
325	123.00	90471.1	628,1	278.1	35 6	242 5
350	168 64	124041 0	601,1	210,3	27.8	182.6
374	225.05	165532.7	501,1	0	0	0

энергией жидкости при 0°. Внешняя скрытая теплота И. при постоянном давлении р g_e=A-p(a-s),

где А—термический эквивалент работы. Полная теплота И.

Я=J С dt -f- ρ_{ + А р (σ — s).

Для воды от 0 до 100° можно пользоваться формулой: ρ=606,5 — 0,695 ί — 0,00011 ί². Для других жидкостей:

Хлороформ.. . ρ= 67,0 - 0,09485t - 0,00005074»

Сероуглерод. . ρ= 90,0 - 0,08922ί - 0,0004938!“

Эфир. ρ= 94.0 - 0,07901ί - 0.00085Ш²

Бензол. ρ=109,0 — 0,13550ί — 0,0008515i^a

С повышением Г скрытая теплота И. уменьшается и при t°_Kpum. ρ=0. Величина д_е с возрастанием ί° сначала постепенно увеличивается и достигает своего максимума обычно при 0,7 абсолютной t°_Kpum_, а затем убывает и при t°_Kpum. ρ„=0, как и ρ,=0.

Самый простой случай И. — с поверхности неподвижной жидкости в покоящийся воздух (статическое И.). На практике мы сталкиваемся с этим случаем при храпении жидкостей (в частности жидкого топлива), в поверхностных увлажнителях, в мокрых производствах и т. д. В природе к этому случаю надо отнести И. из водоемов в безветреную погоду. Основной закон для статического И. дан Дальтоном: количество Q испаряемой в единицу времени жидкости пропорционально площади s испаряющей поверхности, обратно пропорционально давлению воздуха р и прямо пропорционально разности давления насыщенного пара p_sпри данной температуре и давления паров в воздухе p=<pp_s (φ — отношение данного давления пара к p_s):

Q=k s

e p

Опыты Стефана и Винкельмана показали, что закон Дальтона является лишь первым, грубым приближением; однако, для случая испарения воды из водоемов поправки оказываются незначительными. Под скоростью испарения понимают объём паров V_z, испаряющихся с 1 см² площади свободной поверхности жидкости в 1 ск. Для жидкостей, налитых в открытые цилиндрич. сосуды, Стефан и Винкельман нашли, что

V=*“. in,

² h р-ps

где h—«путь диффузии» паров, равный расстоянию от поверхности жидкости до свободного края цилиндра, k_t — коэфф. диффузии паров. Если И. идет в свободную от паров атмосферу, то <pp_s=0. Для изменения коэфф-та диффузии с темп-рой Винкельман дает следующую ф-лу:

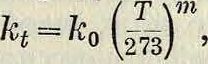
где к₀—коэфф. диффузии при 0°, Т—абсолютная темп-pa, m—постоянная величина, определяемая из опытов. Для диффузии водяного пара в воздух к=0,2162 см²/ск и т=1,774. Коэфф. диффузии и скорость И. зависят от внешнего давления:

к -к ™

lip —

In?—см?Iсм², ск

P-Ps

(ф-ла для И. в покоящийся воздух или газ). Далее, Ил связано и с формой поверхности жидкости и с формой сосуда, внутри которого оно происходит. В средних частях поверхности И. происходит иначе, чем у краев. Неста Томас и Фергюсон нашли для массы Q воды, испаряющейся в 1 ск., ф-лу: Q=kaⁿ, где а — радиус круглой поверхности, к==0,05 + 0,025е-^1й и п=2,0 -0,60 е-²". Не давно (в 1926 г.) В. Шулейкиным разработана кинетическая теория И. Он расчленяет весь процесс И. на три части: 1) вылетание молекул из жидкости — свободное И., 2) обратное поглощение части вылетевших молекул жидкостью (при ударах о ее поверхность) и 3) распространение (диффузию) остальных молекул в окружающей покоящейся газовой среде.

Для скорости И. с безграничной плоской поверхности теория приводит к ф-ле:

ν.=·

1 +

RT_ 2 лт где <pp_s—давление паров в сечении, нахо-

дящемся над поверхностью жидкости на высоте h, ξ—среднее число ударов молекул пара о поверхность жидкости, приходящихся на поглощение жидкостью одной молекулы пара, ν₀—скорость свободного статического

И., равная -i — R— газовая по-

¹ У 2 пт RT

стоянная, т—мол. вес, ρ—скрытая теплота И., к—коэффициент диффузии.

В случае статич. И. с поверхности круга конечных размеров, объём испаряющейся жидкости со всей поверхности равен:

Q=(Vs - VPs) cm^sIck,

где а—радиус круга и у—удельн. объём жидкости. Чтобы оценить статич. И., необходимо знать для паров данной жидкости коэфф. диффузии (смотрите) и его изменение с f° и другими факторами, мол. вес, кривую упругости насыщенных паров и скрытую теплоту И.

Явление И. значительно осложняется, как только от статич. условий мы переходим к д и-намическим. При самом слабом движении воздуха количество испаряющейся жидкости значительно возрастает^. к. увеличи вается коэфф. диффузии: k_w=k₀VW In ~ >

где fc₀—коэфф. диффузии в отсутствии движения воздуха, W—скорость воздуха вдоль испаряющей поверхности в см/ск. Случаи И. в динамич. условиях наиболее часто встречаются как в природе (т. к. обычно имеется или движение воздуха мимо испаряющей поверхности—ветер или, наоборот, движение самой испаряющей поверхности в воздухе— капли дождя), так и в технике, где особенно распространен случай И. жидкости, разбрызгиваемой в струе воздуха (двигатели внутреннего сгорания, работающие на карбюрируемом топливе, И. при пульверизации, и т. д.). Если рассматривать И. капли не слишком малого радиуса а с точки зрения кинетической теории И., то для скорости И. с поверхности капли получим:

V — ^v°. 4s - <PPs) ^s аВ +1 p_s ’

где

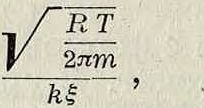
а г>₀ — скорость испарения с безграничной плоской поверхности.

Самым сложным, а вместе с тем и имеющим наиболын. значение в технике является случай И. при карбюрации. Основные процессы здесь следующие: воздух просасывается через карбюратор; создающимся разрежением в струю этого воздуха засасывается из жиклера жидкое топливо, при выходе из жиклера струя топлива разбивается на капли, несущиеся в потоке; вместе с тем начинается И. с капель в ^воздух и диффузия в последнем молекул образовавшихся паров топлива. Значительная часть капель, как показали опыты в Научном автомоторном институте (НАМИ), вскоре оседает на стенке трубопровода и образует пленку жидкого топлива, движущуюся по трубе значительно медленнее (раз в 60) воздуха. С поверхности этой пленки тоже происходит И. топлива в воздух. В результате И. с поверхности капель и с пленки жидкого топлива и диффузии молекул пара, в струе воздуха происходит смешение паров топлива с воздухом, и образуется горючая рабочая смесь.

Попытка дать теорию динамич. И. принадлежит Кляфтену. Им построена теория И. с капель, прямолинейно движущихся в потоке воздуха и равномерно в нем распределенных. Кляфтен исходил из основного уравнения классической теории диффузии газов (в полярных координатах):

θ(φΡε) _ 1 Г d²(w>s), ² d(PPs)"|

dZ L да‘ -Га да ’ где a—радиус капли, Z—время, p_s—давление насыщенных паров, к—коэфф-т диффузии. Интегрирование этого ур-ия дает:

sin (Аа) г, ~Α4ιΖ VPs ⁼ Ал где __

α₀ у п sin (Αα„)

Аа₀

а„—радиус капли в момент начала И., п— коэфф. смешения, то есть отношение веса воздуха к весу жидкости и паров, п—коэфф.

смешения для случая, когда насыщение наступает при Ζ=со. Теория Кляфтена очень несовершенна, так как не учитывает целого ряда очень важных факторов (упругости насыщенных паров около капель в зависимости от формы и размеров поверхности последних, неоднородности распыливания,наличия вихревых движений воздуха, И. с пленки ит. д.). Вследствие этого время полного И. капель, по теории Кляфтена, получается слишком малым, что не согласуется с данными, полученными из моторной практики. Таким образом, полной теории динамического И. пока еще нет, и оценку И. приходится давать, лишь основываясь на сравнительных опытных данных.

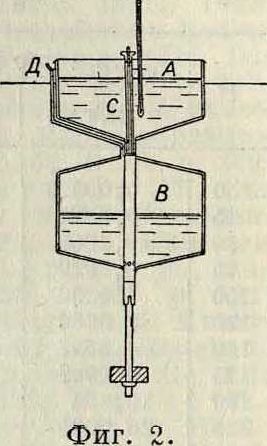
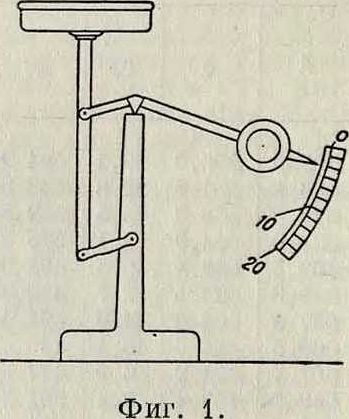
Для измерения И. с покоящейся жидкости служат особые приборы, называемые испарителями, или эвапорометрами. Самый простой и наиболее распространенный из них—испаритель Вильда (фигура 1). Па чашку неравноплечных весов наливается жидкость (слой толщиной 20 миллиметров). При И. чашка делается легче, и уравновешивающий ее груз опускается. Стрелка показывает, сколько жидкости испарилось. Очень распространен для воды испаритель Лер-мантова (фигура 2), состоящий из двух соединен. друг с другом сосудов А и В. В испаритель наливают воду, пока не заполнится весь нижний сосуд (воздух из него выходит через трубку Д). Затем мехами через трубку Д

нагнетают в нижний сосуд воздух, этим подымают воду в верхний сосуд и закрывают соединительную трубку пробкой С. Вода испаряется в течение определенного времени из верхнего сосуда. Чтобы узнать, сколько испарилось воды, открывают пробку С, спускают воду в нижний сосуд и приливают мензуркой дополнительно новую воду, пока в нижнем сосуде не будет достигнут прежний уровень. В лабораторных условиях скорость статич. И. можно измерять или в открытых цилиндрах, по понижению свободного уровня жидкости (метод Винкельмана), или в закрытых цилиндрах по парциальному давлению паров. Для измерения И. в условиях, возможно близких к тем, какие имеются во всасывающих трубопроводах мотора (дина-мич. И.), НАМИ осуществлена следующая установка (фигура 3). Жидкое топливо через карбюратор К подается в трубу Τ, через которую просасывается с помощью компрессора воздух (со скоростью до 40 м/ск). Часть топлива, образующая пленку на стенках трубопровода, в конце последнего улавливается захватными кольцами и стекает в собирательный сосуд С,. Оставшиеся неиспарен-ные капли падают на рупорный экран Рэ и стекают в собирательный сосуд С₂. Т. о. оказывается возможным уловить всю неис-парившуюся в трубе часть топлива, а отсюда узнать и количество испарившегося топлива.

Во всех случаях И. жидкость может испариться нацело лишь в количестве, к-рое соответствует давлению насыщения. Упругость насыщенного пара является важнейшим фактором для процесса И. Чем больше упругость насыщенных паров при данной Г, тем больше для насыщения требуется вещества, тем большее количество жидкости может испариться. Упругость насыщенных паров

Фигура 3. Пленки Капель

Не испарившиеся остатки равняется атмосферному давлению при t°_Kun,. Отсюда, чем ниже ί°_ΚΜ„. данной жидкости, тем последняя более «летуча», тем сильнее она испаряется.

Если обратимся к сложным жидкостям, являющимся смесями из целого ряда компонентов (а таковы все наши жидкие топлива—бензины, керосины, нефть, технические или моторные бензолы и т.д.), то они выкипают уже не при одной έ°, а по фракциям. Так, в техническ. бензоле, представляющем смесь бензола, а, ксилола и сольвент-нафта, должна была бы сначала, ок.80° выкипать бензольная фракция,затем, ок. 110°— ьная, ок. 130°—ксилольная ит. д. На самом же деле кипение начинается действительно ок. 80°, но жидкость при дальнейшем подогреве продолжает все время нагреваться, и кипение идет непрерывно до тех пор, пока все, даже трудно испаряющиеся фракции не улетят. Для характеристики таких сложных жидкостей служит т. н. кривая разгонки (фигура 4), дающая % по отношению к первоначальному весу (в технике часто к объёму) испарившейся части

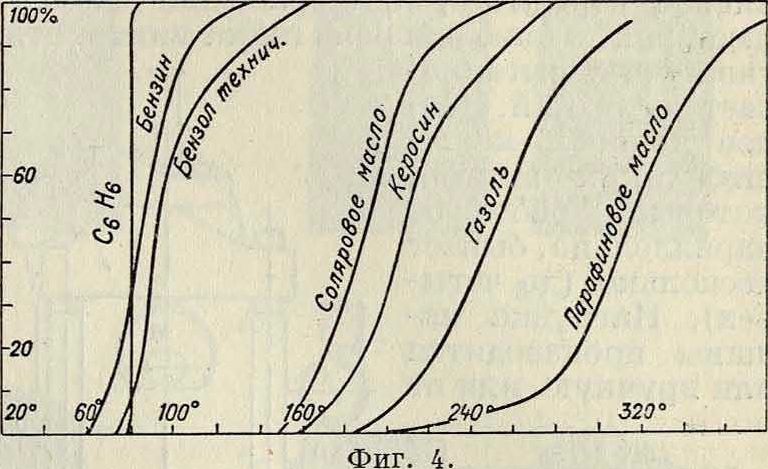
жидкости до данной ί°. Законы И. смесей очень сложны и до сего времени не выяснены.

Лит.: Хвольсон О. Д., Курс физики, т. 3, Берлин, 1923; Любославский Г., Основания учения о погоде, П., 1915; Вишняков С. И., Теория карбюрации и расчет карбюраторов, М., 1927; Шулейкин В. В., Кинетическая теория испарения, «Ш», ч. физич., 1928, т. 50, стр. 527; Hans-brand Е., Verdampfen, Kondensieren u. Kiihleu, 6 Aufl., B., 1918; Klaften Z., «Motorwagen», В., 1921, Η. M, 13, 14; Н e i η 1 e i n F., Experimented Untersuchung d. physikalischen Eigenschaften mitt-lerer u. schwerer Brennstoffe, ibid., 1926, H. 4, 8, 26, 31; Fomin W. und I г i s s о w A., Methoden z. Verdampfungsuntersuchung fliissiger Brennstoffe, ibid., 1929. А. Ирисов.