 > Техника, страница 50 > Исчисление бесконечно малых
> Техника, страница 50 > Исчисление бесконечно малых
Исчисление бесконечно малых
Исчисление бесконечно малых,
часть высшей математики, включающая дифференциальное и интегральное исчисление и характеризуемая специальным методом, применявшимся еще Архимедом (в неявном виде) для вычисления площадей криволинейных фигур (круга, параболы). В полной мере этот метод был развит одновременно Ньютоном и Лейбницем (17 в.); однако, строгую логическую основу он получил лишь в 19 в работах Коши и Вейерштрасса. В основе современного метода И. б. м. лежит понятие переменной величины. Буквенная величина называется переменной, если (в данном рассуждении) она может принимать разные численные значения; если же величина сохраняет одно и то же численное значение, то она называется постоянной (всякое число есть величина постоянная); например: в формуле равномерного движения s=vt скорость V есть величина постоянная, а время t и пройденное расстояние s—переменные величины. Переменная, которой мы можем давать произвольные численные значения, называется независимой переменной (или аргументом); переменная, численные значения которой определяются значениями независимой переменной (или переменных), называется зависимой переменной (или функцией). В нашем примере t есть независимая переменная, as—ф-ия от t. Функция определена, если каждому значению аргумента соответствует определенное значение функции. Эта зависимость м. б. задана графически, таблицей (таблицы логарифмов, синусов) или ф-лой. Выражение «у есть ф-ия от х» символически записывается так: у=/(ж). Если z есть ф-ия двух независимых переменных ж и у, то это запишется так: z=f{х, у). Если ф-ла, определяющая ф-ию, содержит только действия сложения, вычитания, умножения и возведения в целую степень над независимой переменной, то это — ф-ия целая рациональная (она м. б. представлена в виде многочлена), например: у=ж2 — |ж+8; если же в формулу входит деление, то имеем ф-ию дробную рациональную, например: У=~· Если в ф-ии у=fix) или же при нахождении у из ур-ия /(ж,2/)=0 независимая переменная находится под знаком радикала, то мы имеем иррациональную ф-ию, например уг — ж=0, или у=Vx. Рациональные и иррациональные функции называются алгебраическими. В последнем примере всякому значению ж > 0 соответствуют два значения у (два знака перед радикалом); мы имеем функцию двузначную. Все функции, не являющиеся алгебраическими, называются трансцендентными, например sin ж.
Бесконечно малые величи-н ы. Если переменная величина изменяется так, что ее значения по абсолютной величине становятся (и остаются) меньше любого наперед заданного положительного числа ε, то переменная называется бесконечно малой. Так, величина ~ — бесконечно мала при неограниченном увеличении абсолютного значения ж; в самом деле | * j < ε для всех значений ж, для которых | х |"> -, например |^| <0,01, если только | х | > 100. Далее, sina;—бесконечно малая при достаточно малом ж, т. к. I sin ж | всегда меньше х и, следовательно, | sin ж | < е, если | ш j < ε. Из постоянных величин только 0 удовлетворяет определению бесконечно малого.
Теоремы о бесконечно ма-л ы х; 1) алгебраич. сумма ограниченного .числа бесконечно малых бесконечно мала; 2) произведение бесконечно малой а на ограниченную величину β (то есть существует такое положительное число М, что β <М при рассматриваемых значениях β) бесконечно мало; в частности, произведение двух бесконечно малых бесконечно мало.
Предел. Если переменная у изменяется так, что разность между ней и некоторой постоянной Ь становится бесконечно малой β, то говорят, что предел у есть Ь; это записывается так: limу=Ь, или Из определения предела следует, что у=Ь + β (β—бесконечно малая) или что у — Ь м. б. сделана < е. Очевидно, предел бесконечно малой величины есть 0. Если переменная при своем изменении становится по абсолютной величине больше любого положительного числа М, то есть [ у > М, то у называется бесконечно большой; бесконечно большая величина не имеет предела, но условно говорят, что предел у в этом случае равен бесконечности: Пт у=оо, или у -»оо, например:
Пт sin ж=0; lim-=0; lim tg сс=со ·.
X —> 0 Ж—>со Х π
£С—> -
Теоремы о пределах: 1) предел постоянной равен этой,постоянной; 2) предел алгебраич. суммы переменных равен алгебраической сумме пределов; 3) предел произведения равен произведению пределов; 4) предел частного равен частному пределов, если только предел делителя =£0;
в случае, если предел делителя равен 0, а предел делимого Ф 0, мы имеем бесконечно большую, ее предел (в условном смысле) есть со; если же и предел делимого равен 0, то имеем неопределенный случай (предел отношения двух бесконечно малых).
Здесь может существовать предел, но его нахождение требует каждый раз особых рассуждений; так, доказывается, что lim=1 (смотрите Дифференциаль
ное исчисление, Неопределенные выражения). Точно так нее неопределенным является предел отношения двух бесконечно больших величин, но иногда его можно вычислить после преобразования выражения,
на основании общих теорем, например:
·,. 2хг - х + 4.
lim —5—г—= lim
2-Tl + d;
-=lim-==2.
X —V m 1
Понятие предела является основным в дифференциальном и интегральном исчислении.
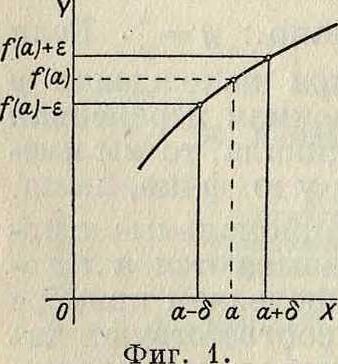
Непрерывность функции. Рассмотрим значение ф-ии /(ж) при ж=а, то есть (а), и значения той же ф-ии при близких к а значениях х. Если изменение ф-ии бесконечно мало при достаточно малом изменении х, то говорят, что (ж) непрерывна в точке х=а. Это можно записать так: для любого (сколько угодно малого) ε > 0 найдется достаточно малое <5 > 0 такое, что |/(ж) — f(a) | < ε, как только I ж — а I < <5 (фигура 1). Пользуясь определением предела, непрерывность при х=а можно выразить так: Пт /(*)=/(»), то есть предел х-Фа функции равен значению функции в предельной точке. Ф-ия, непрерывная в каждой точке отрезка, называется непрерывной на отрезке. Если в точке х=а
условие непрерывности не выполнено, ф-ия называется разрывной при х=а. Так, если при х Ф 0 Дж)=0, а/(0)=1, то ф-ия разрывна при ж=0, т. к. предел функции равен 0, а значение в предельной точке=1.
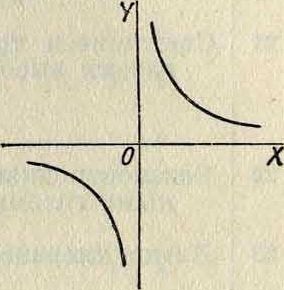
Ф-ия у=arc tg i разрывна при ж=0, так как, если ж приближается к 0 по положительным значениям, то предел ф-ии равен если же х приближается к 0 по отрицательным значениям, предел равен— то есть lim arc tg i
“ X—> 0 Х
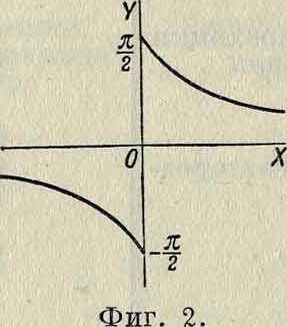
не существует (фигура 2). Ф-ия у=* имеет разрыв при ж=0, т. к. предела в истинном смысле слова нет: он равен сю (фигура 3). В анализе бесконечно малых, и особенно в приложениях, мы имеем дело гл. обр. с непрерывными функциями.
Лит.: см. Дифференциальное исчисление и Интегральное исчисление. В. Степанов.