> Техника, страница 50 > Исчисление конечных разностей

Исчисление конечных разностей

Исчисление конечных разностей,

отдел математическ. анализа. В дифференциальном исчислении (смотрите) мы даем аргументу ф-ии приращение, к-рое является бесконечно малым (стремится к 0); в И. к. р. мы ограничиваемся конечными приращениями аргумента, равными некоторому постоянному числу h. Основным понятием является разность ф-ии, A fix):

^Δ/(*)=/(* + h)-f(x)

Разность есть ф-ия от ж; ее разность есть 2-я разность, Δ²/(ж):

ΔΔ /(ж)=A² fix)=fix + 2h) - 2/(ж + h) + fix).

Аналогично определяются разности 3-го,

4-го,., те-го порядка. Мы можем ограничиться рассмотрением случая ln=1, так как общий случай сводится к этому заменой переменного: x=hy.

Разности простейших функций. ДС=0 (С—постоянная); Ах=h Aa^x=a^XJrh—

— а^х=a^x(a^h -1); Δ sin x=2 cos (x + sin |;

Δ cos x=— 2 sin (x + sin ~ ·

Разность ф-ии ж“ или любого многочлена те-й степени есть многочлен (и—1)-й степени, разность (те+1)-го порядка от многочлена и-й степени есть 0. Но более простые формулы получатся, если вместо степеней ввести факториальные функции

x(x-h).[x-еп-т и _(x+hKX+2к)._{х+щ >

разности

Δ х(х — К). х — {п — 1 )h] =

= nhx(x — К). [х — (п — 2)h ] и

. 1 _ -nh _

(x+h)(x- -2h). (x+nh) ~ (x+h)(x+2h). [x+(n+l)/i]

тоже факториальные функции с числовым множителем.

Основные формулы И. к. р. аналогичны формулам дифференциального исчисления; отметим разность от произведения:

Δ [/(ж) · φ(χ)]=ψ(χ + h)A /(ж) + /(ж) Δ φ(χ). Роль ряда Тейлора в И. к. р. играет ряд Ньютона, являющийся разложением данной функции по факториальным функциям. Он пишется так:

/(ж)=/(0) + ~^ ж + ^ ж(ж - К) +

+ x(x-h)(x-2h) +.

Этот ряд применяется для интерполяции (смотрите Вычисления приблиэюенные).

Пример. Разложить ж³ по факториальным ф-иям при h= 1. Имеем:

Δ ж³=(ж + I)³ — ж³=Зж² + Зж + 1;

Δ²ж³=6ж + 6; Δ³ж³=6; Д⁴ж³=0. Подставляя в эти равенства значение ж=О и обозначая символически {А^кх ^!)·=ο=Δ* 0^г, имеем: Δ О³=1, Δ² О³=6, Δ³ О³=6. Итак: ж³=ж + Зж(ж — 1) + ж(ж — 1)(ж — 2). Операция, обратная нахождению разности, называется суммированием; если

Δ <р(х)=f(x), (1)

то имеем:

<р(а + h)~ <р(а)=f(a),

<р{а + 2 h) — φ(α + h)=f(a + h),

φ(α + nh) - φ[α + (η-1 )fe]=f[a + (те -1 )h].

Отсюда, складывая почленно, имеем:

i=n-i

2 /(« + Щ=φ(α + nh) — φ(α) =

-ИГ· <²>

Ф-ия φ, удовлетворяющая условию (1), называется иногда неопределенным интегралом по конечным разностям и обозначается знаком Sf(x);

он определяется с точностью до произвольной периодич. ф-ии периода h формула (2) показывает, что конечная сумма в левой части получается подстановкой значений ж, x+nh в неопределенный интеграл по конечным

a+nh

разностям; это записывается так: ^ /(ж).

а

Пример 1. Найти сумму 1³ + 2³ + .+ + (и — I)³. Здесь /(ж)=ж³, h=1. Заметим, что неопределенный интеграл по конечным разностям от факториала выражается так:

S ж(ж — h). [ж — (те — l)h]=ж(ж — h). (х-nh),

(re +1 )h

следовательно,

S ж³=S [ж + Зж(ж — 1) + ж(ж зс(х-1)

+ ж(ж — 1)(ж — 2) +

х(х

-1)(ж-2)] =

• 1)(х - 2)(х - 3)

п-ι п _

Искомая сумма V т³=5*ж³=^:

_Λ>·, л η *-

х(х -1)

+

+ж(ж—1)(ж—2) +

х(х-1)(х-2)(х-3)

]=в-т

Пример 2. Путем обращения ф-лы разности для cos х находим

S sin ж=— -

2 sin -

Отсюда получаем:

sin а + sin (а + h) +. + sin [а -f (те — 1 )h ] =

a+nJi COS

= 5 sin x=—

^a 2 sin ^

sin [o + (re - l)h] sin nh ~. h

sm 2

В связи с суммированием, в И. к. р. большую роль играют функции Бернулли. Их можно определить как неопределенный интеграл по конечным разностям: те-я ф-ия Бернулли

?·*(*)=$ рплут ·

Это—многочлен те-й степени вида

Х^п, _λ ЗС^,г_1

(η — 1)!

-числа они определяются ур-иями:

А₀, Αι, Αγι-2

Ψη (ж)=Αο_Ή + Α₁-

Здесь А₀, А_г, А_г.-

+ ··. + А_п_₁х. Эйлера;

: 4-

П ¹ (П

П+-+Т^ + Α_Κ_1=°;

1)1 ··· 1.2 -4₀=1; -4-i=₂ ; те — 3,

4, 5.

При этом оказывается, что П₃=А₅=.=0. С помощью чисел Эйлера выражаются ч и с-ла Бернулли (смотрите Бернуллиевы числа): В_к= (-1)·-¹· 1-2·. -2fc-A₂*

и суммы вида 2 11=1

1

_n27; ’

именно:

А - (-¹)··² Λ i L. i _L J. i

(2π)2ί ^ ‘ 22Λ+ 32& “i^- 42λ "T" ··“; *

В частности, l +1 +1 +.=ί.

Формула суммирования Эйлера выражает связь между интегралом по конечным разностям и обыкновенным интегралом:

,§/(*)=s /(*)^dx + ^А1Ш-ПР)] + [/(ж)-

о о

(з)

В этом ряду R_n не стремится к 0,—ряд расходится; но для нек-рого значения п остаточный член мал, и конечная сумма дает хорошее приближение. В наиболее важном случае, когда f(t), f^v (ί),. имеют одинаковый знак, a/(i), /"(f),. бесконечно малы при бесконечно большом f, имеем:

R_ik=0A,_ikf^fi-^r x).

Ф-ла (3) применяется для приближенного вычисления суммы через интеграл или, наоборот, для приближенного вычисления определенного интеграла. С ее помощью доказывается формула Стирлинга:

In(1- 2· 3·. · п)=1пУ2л+ + Inп—п + + A₂n-¹ + A_il- 2-п~*+ ., откуда приближенно:

ni ^п^пе~^пУ2лй.

Уравнения в конечных разностях. Будем полагать h=l и обозначать: f{x)=y_x, f(x + l)=y_x+i,. Разность А^пу выразится линейно через у_х, у_х+1,., у_х+_п. Ур-ие в конечных разностях п-то порядка есть соотношение между х, у_х и разностями до и-го порядка включительно, которое можно написать в виде

^ф(х, Ух, Ух+1, ,Ух+_п)=0.

Для техники наибольшее значение имеют линейные уравнения в конечных разностях с постоянными коэфф-тами, то есть ур-ия вида

Ух+п+PiVx+n-i + · · · + Pn-iVx+i+РпУх=q, (4)

где р_и Vi, ·, Рп—постоянные числа, у—данная ф-ия х. Если q= 0, имеем однородное уравнение. Для решения однородного ур-ия ищем частное решение вида у=а^х, для определения а получаем ур-ие п-й степени:

а^п + pjffl”-¹ +. + 2Wi + р_п=0.

Если его корни—а_х, а₂, ., а_п (различные), то общее решение однородного уравнения имеет вид:

Ух=c_xaf + с₂а^х2 +. + с_па^х.

Для определения постоянных с_х, с₂, ., с_пдолжен быть заданы значения у₀, у_и ., у_п-_х. Если 2 корня—мнимые сопряженные, например а_х=g(cos ψ + г sin φ), а₂=ρ(οos φ — i sin φ),

то соответствующие решения будут: q^xcosx<p, ρ*βίη χφ. Случай кратных корней требует особого рассмотрения. Для общего ур-ия (4), если q постоянно, находим частное решение:

1 + р₁ + р_1!+. +Рп~ Р ’ где β—постоянное число; тогда y_x=c_xaf +. +ο_ηαζ + β.

Пример. Требуется определить опорные моменты равномерно нагруженной горизонтальной балки, причем все опоры одной высоты h, расстояния I между опора ми равны и величина нагрузки q (смотрите фигура). Уравнение, связывающее моменты

М_к + 4 М_к+1 + М_к+2 — — - qV,

есть линейное ур-ие в конечных разностях. Общее решение соответствующего однородного ур-ия есть М_к=с_х×+ с₂Я|, где λ_χ и λ₂—

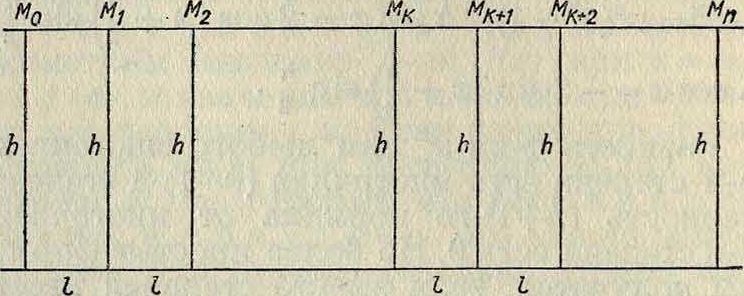
корни характеристич. ур-ия λ²+4Λ+1=0, Я₁₂=— 2 + УЗ. Частное решение β=— --¹- Итак,

Ш_к=сЛ + сА-^·

Для определения с_х и с₂ замечаем, что М₀=0,

<П

М_п= 0, то есть с_х+с₂

qj+ Я«--1 QV

12 a?-ji« > ₁₂

откуда с_х= -

Я‘‘-1

Кро-ур-ия И. к. р.

>

ме строительной механики, применяются в электротехнике (в расчете катушек) и др.

Лит.: Селиванов Д., Курс исчисления конечных разностей, СПБ, 1906; Марков А., Исчисление конечных разностей, 2 изд., Одесса, 1911; N о г 1 u n d N., Vorlesungen iiber Differenzenrechming, Berlin, 1924. В. Степанов.