> Техника, страница 51 > Капиллярные явления

Капиллярные явления

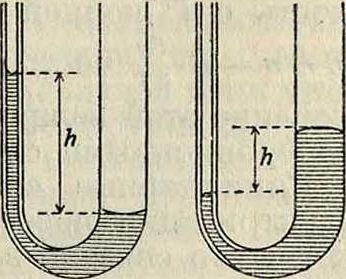
Капиллярные явления, в собственном смысле слова, явления, состоящие в том, что, например, в сообщающихся сосудах, один из которых состоит из узкой (капиллярной) трубки, жидкость устанавливается в равновесии не на одинаковой высоте. При этом жидкость, смачивающая внутренние стенки трубки (в случае стекло—вода), устанавливается в капилляре выше, чем в сообщающемся с ним широком сосуде (фигура 1, а). Не смачивающая же жидкость, например ртуть (фигура 1,6), стоит в узкой трубке ниже этого нормального уровня и обнаруживает т. н. депрессию (смотрите Барометр).

Всасывание жидкостей пористыми телами (куски сахара, кирпич, поч- ^а 6

ва) также относится к фигура 1.

капиллярным явлениям и имеет большое прикладное значение, .особенно для почвоведения (смотрите).

Все К. я. обусловлены силами междумо-лекулярного сцепления, действующими как между частицами жидкости, так и между частицами твердой стенки и соседними частицами жидкости.

Основными величинами при изучении К. я. служат: внутреннее давление К (молекулярное давление на плоской поверхности жидкости, см. Жидкости), поверхностное

натяжение а, определяемое как работа образования единицы (1 см²) новой поверхности раздела, и краевой угол &—угол, образуемый жидкой поверхностью с пересекающей ее твердой стенкой. Краевой угол дает возможность измерять смачиваемость твердой стенки; за меру ее удобно принять величину В= cos#. Поверхностное натяжение а является той избыточной свободной энергией, которой слой жидкости вблизи поверхности раздела обладает по сравнению с ее внутренними частями. Поэтому поверхность жидкости S самопроизвольно уменьшается (это связано с уменьшением свободной энергии ψ=а S всей поверхности жидкости) и принимает под действием одних только междумо лекулярных сил форму шара, отвечающую при данном объёме наименьшей поверхности жидкости; другой возможный самопроизвольный процесс, связанный с понижением свободной поверхностной энергии жидкости, состоит в скоплении у поверхности раздела таких веществ из окружающей среды (например, растворенных ранее в самой жидкости), которые своим присутствием в поверхностном слое понижают а. Гиббс термодинамически показал, что скопление, то есть адсорбция (смотрите), таких «поверхностноактивных» веществ у любой поверхности раздела необходимо связано с понижением свободной поверхностной энергии этой поверхности, что количественно выражается ур-ием вида: Г= — ~ · ^, где Г — адсорбция в г-мол/сж², с — концентрация в растворе, а до

— _дс~ поверхностная активность,

мера способности вещества понижать поверхностное натяжение. Поверхностное натяжение убывает с t° для чистых жидкостей почти линейно, обращаясь в 0 в критич. точке смешения обеих фаз, образующих поверхность раздела. Поверхностное натяжение адсорбционных слоев (в случае растворов поверхностноактивных веществ) убывает с t° не линейно, а по резко изогнутым кривым, иногда же может и возрастать с ί° в нек-ром интервале (Ребиндер), т. к. адсорбция, снижающая поверхностное натяжение, сама всегда убывает с t°. Этим объясняется и неизменяемость с 4° полной поверхностной энергии

Е=σ — Т -~г чистых жидкостей и резкое изменение этой величины Е для растворов с адсорбционными слоями.

Капиллярные свойства (σ) зависят от электризации поверхности, в особенности, когда это связано с изменением концентрации ионов вблизи поверхности, изменяющих а по ур-ию Гиббса. Такие явления, наблюдаемые обычно на ртутном мениске в растворах электролитов, называются электро-капиллярными явлениями и изучались Липманом, Гуи, Фрумкиным и др.

Теория капиллярности исходит из представления о силах, действующих между молекулами лишь на чрезвычайно малых расстояниях г; с увеличением г эти силы быстро убывают, практически обращаясь в 0 при расстояниях r^S, где <3—т. н. радиус сферы молекулярных взаимодействий. Легко показать, что δ есть одновременно и толщина поверхностного слоя, то есть того слоя у поверхности жидкости, молекулы к-рого, втягиваясь внутрь лежащей под ними жидкостью, обусловливают внутреннее давление. Поверхностное натяжение а и есть работа извлечения из внутренних частей жидкости в поверхностный слой п числа молекул, необходимого для образования нового 1 см², поверхности (смотрите Жидкости). Экспериментальные данные последнего времени показывают с очевидностью, что толщина поверхностного слоя, а следовательно и радиус сферы действия, совпадает с диам. молекулы (обычно порядка 5 х 1СГ⁸ см); отсюда следует, что поверхностные слои обычно мономоле-кулярны и что только ближайшие соседи данной молекулы обнаруживают с ней заметное взаимодействие. Первый основной закон теории капиллярности (1-й закон Лапласа) состоит в том, что в общем случае искривленной поверхности жидкости полное внутреннее давление р отличается от молекулярного. давления на плоской поверхности К на величину Л=σ.

ρ-Κ+Π-Κ + σ^+£. (1)

Здесь R_lt Л_г—радиусы главной кривизны в данном месте поверхности, считающиеся положительными,когда они направлены внутрь жидкой массы. Итак, поверхностное натяжение эквивалентно некоторому добавочному внутреннему давлению сг(-^ + ^-)=Я, называемому капиллярным давлением. Из (1) получаем ур-ие свободной поверхности жидкости, не подверженной действию внешних сил: +1,=Const. Эта поверх-

-К i 2

ность будет поверхностью постоянной средней кривизны (минимальной поверхностью). Поверхность шара как раз и является такой замкнутой поверхностью. В случае шара

П=д-. Уравнение (1) позволяет объяснить большое число разнообразных явлений. Так, внутфи малого сферич. пузырька, находящегося в равновесии внутри жидкости,

давление должен быть на П=больше, чем давление атмосферы над плоской поверхностью жидкости на том же уровне. При весьма малых пузырьках с радиусом R^l μ это избыточное давление делается весьма значительным (смотрите таблицу).

Избыточное капиллярное давление внутри пузырька, образовавшегося в воде (при ί°=20°, σ=72,8 эрг/с-н²).

R	Я в дин/см2	П в atm
1 см..	146	~ 1,10-*
1 миллиметров..	1 460	~ 1,10-3
0,1 миллиметров.	14 600	- 1,10-*
1 μ..	1 460 000	г~ 1,5
0,1 μ..	14 600 000	~15

На этом явлении основана капиллярная теория перегревания жидкостей Дюгема (и вообще капиллярная теория задержек при появлении новой фазы и метастабильных состояний). По той же причине давление насыщенного пара над поверхностью малых капель больше, чем над плоской поверх-

ностыо, как это показал термодинамически Кельвин. Давление внутри выдутого мыльного пузыря на 2Л=больше, чем снаружи. Чтобы выдуть пузырек воздуха из капиллярного отверстия, на глубине Н сантиметров под поверхностью жидкости плотности Ώ надо преодолеть, кроме гидростатического давления Н D g, еще и избыточное капиллярное

Я=— ; т. о., наибольшее давление образова-

Ϊ* 2а ния пузырька будет (по Кантору) р=—+

+Н D д, где г—наименьшее значение радиуса R пузырька во время его образования, равное радиусу отверстия. Измеряя р манометрически и зная г, легко найти а. Внутреннее давление на поверхности мениска в узкой трубке (радиуса г), вполне смачиваемой жидкостью, на у меньше (г отрицательно,

т. к. мениск, принятый полусферическим, вогнут), чем на плоской поверхности жидкости в широком сообщающемся сосуде. Поэтому для равновесия жидкость должна стоять в капилляре настолько выше (Я), чтобы гидростатическ. давление избыточного столба H-D-g уравновешивало П, то есть чтобы

П +11 D з=0 или, т. к. Я=— у,

α^ϋψΣ.Η-, Н=^. (2)

Это—закон поднятия жидкости во вполне смачиваемом ей капилляре, позволяющий определить поверхностное натяжение жидкости а по высоте поднятия Я в капилляре данного радиуса г. Из ур-ия (2) видно, что Н обратно пропорционально г, то есть что произведение Hr есть величина для разных капилляров постоянная, зависящая только от свойств жидкости и называемая капиллярной постоянной:

o’-Н-г; а“-~-; (3)

а² имеет размерность площади и измеряется в миллиметров- или в см², тогда как а имеет размерность эрг/сж.². Для жидкости, не вполне смачивающей капилляр, вместо (2) имеем:

2 cos # ( )

Ниже приведены значения а в эрг/елг² для нек-рых жидкостей на разных поверхностях раздела при t°=20° (σ убывает с ростом взаимной растворимости обеих фаз):

Вода (Н_гО)—воздух.. 72,75 + 0,05

Ртуть (Hg)—воздух..460

Этиловый (С2Н50Н)—воздух. 22,0

Этиловый эфир (СШюО)—воздух. 16,5

Вода—бензол (С_вН.).. зз,о

Вода—анилин (C«H₅NHj). 8,0

Вода—изобутилов. (г-С.,Н)ОН) 1,8

Вода—этиловый. 0

Когда поверхность жидкости не свободна, а окаймлена, то есть пересекается твердой стенкой, к первому закону надо добавить т. и. второй закон теории капиллярности:

^ff2,3-^ffM=<4,2-cos#. (5)

Это условие определяет краевой угол & или смачиваемость В=cos $ через три поверхностных натяжения (фигура 2): <г_1>3—на границе стенка 3—нижняя жидкость 1; а_{2 г}— на границе стенка 3—верхняя жидкость или воздух 2; ffj j—на границе раздела двух жидкостей 1—2 (или на границе жидкость 1—·

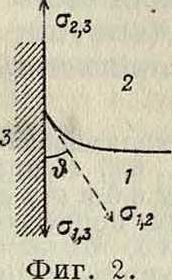
воздух 2).Т. о., ур-ие (5) применимо и к общему случаю двух наслоенных друг на друга жидкостей, поверхность раздела которых пересекается твердой стенкой. Из ур-ия (5) следует, что на твердое тело, наир, цилиндрик с вертикальной боковой поверхностью, помещенное в поверхностном слое, действует, вообще говоря, кроме обычных, сил тяжести и гидростатических, сил, еще и сила смачивания (ф л о т а ц и-онная сила):

F=L σ cos&, (6)

где L—периметр сечения твердой стенки жидкой поверхностью раздела. Когда В>0, в случае лучшего смачивания стенки нижней жидкостью 1—водой (гидрофильная стенка), добавочная сила F> 0 и направлена вниз; когда же Я<0 (стенка гидрофобна, то есть лучше смачивается жидкостью 2), сила F< 0 и направлена вверх (фигура 3) и при достаточно малых размерах твердого кусочка (когда L велико сравнительно с объёмом v кусочка) превышает силу тяжести даже при значительных плотностях твердого материала. Условие флотации будет (по Ребиндеру): F+Ρζζ0;

[водная среда

Фигура 3.

= к — σ В > 1; здесь Р—сила тяжести,

— I

I Р I Ώ

действующая на твердую крупинку, к зависит от плотности твердого тела и обеих жидкостей. Это объясняет «плавание» на поверхности жидкости тяжелых, несмачи-ваемых ей твердых телец (например иголки на воде) (смотрите Флотация), в противоположность требованиям обычной гидростатики, полагающей В=0, #=90°, то есть не учитывающей междумолекулярных сил (силы F).

Флотация из всех К. я. нашла наиболее широкое применение в технике для обогащения металлич. руд. Крупинки размолотой металлич. руды, лучше смачиваемые маслом, при взбалтывании с водой и несколькими каплями масла или аналогичного реагента остаются в поверхностном слое, тогда как землистая пустая порода, лучше смачиваемая водой, хотя и более легкая, целиком оседает на дно; для перемешивания продувается воздух, причем образующаяся пена уносит на своей поверхности все крупинки руды.

Законы капиллярности применяются также к исследованию условий образования и формы капель. Вес отрывающейся капли пропорционален поверхностному натяжению ее: Р=ка, где к зависит от радиуса шейки капли и от условий смачивания ей кончика. Получая из пипетки один и тот же вес жидкости, можно приближенно считать, что число капель обратно пропорционально поверхностному натяжению; на этом основано измерение σ по счету капель в сталагмометре Траубе.

Капиллярный анализ состоит в том, что в раствор смеси, например, нескольких красок, погружают полоску фильтровальной бумаги. Различные компоненты раствора поднимаются по полоске на разную высоту; разрезая полоску на зоны, можно изолиро-

вать и изучить каждый компонент в отдельности. Измерения поверхностного натяжения все чаще применяются в технике, особенно для определения присутствия сильно поверхностноактивных веществ (сивушные масла и др.).См. Поверхностное натяжение, Эмульсии, Смачивание.

Лит.: Давидов А., Теория капиллярных явлений, 2 ч., Москва, 1851; Иоффе А. Ф., Лекции по молекул, физике, 2 изд., П., 1923; Ребиндер П. А., Научные основы флотационных процессов, «Научное слово», М., 1921, 1; его же, Свойства и строение поверхностных слоев в растворах, сборы. «Молекул, силы и их электрич. природа», под ред. Б. В. Ильина, гл. 4, М., 1928; Фрумкин А. Н., Электрокапиллярные явления, Одесса, 1919; L а-р 1 а с e Р. S., ТгаИё de mdcanique cdldste, t. 4— Suppi, au livre 1, Paris, 1806; Gauss C. F., Alls. Grundlagen и. Theorien d. Gestalt v. Fliissigkeiten in Zustand d. Gleichgewicht, «Ostwald’s Klassiker d. exakten Wissenschaften», Lpz., 1903, 13S; Gibbs J. W., Thermodynamlsche Studien, Leipzig, 1892; M a-tkieu E., Theorie de la capillaritd, P., 1883; P 1 a-teau J., Statique exper. et thdorique des liquides soumis aux seules forces rnoleeulaires, vol. 2, P., 1873; DuhemP., Application de la thermodynamique aux phenomilnes capillaires, «Ann. de l’Ecole normale», P., 1885, p. 207; Minkowski H., Kapillaritat, EnzykI. d. math. Wissenschaften, B. 5—Physik, T. 1, H. 4, p. 558, Lpz.—B., 1907; Poisson S. D., Nou-velle thdorie de l’action capillaire, P., 1831; V an d e r W a a 1 s J., Kontinuitat des gasformigen u. fliissigen Zustandes, p. 103, Lpz., 1871; Van der Waals J., Therinodyn. Theorie der Kapillaritat, «Ztschr. f. phys. Chemie», Lpz., 1894, В. 13, p. 657; Vander Waals und К о h n s t a m m, Lehrbuch d. Thermodynamik, В. 1, § 67—68, Lpz.—Amsterdam, 1908; Bakker G., Kapillaritat, Handb. d. Experimentalphysik, hrsg. v. Wien u. Fr. Harms, B. 7, Lpz., 1928; Freund-1 i c h H., Kapillarchemie, 3 Aufl., Lpz., 1923: P о i n-c а г ё H., Lepons sur la capillaritd, P., 1895; Rie-d e а I E. K., Surface Chemistry, I,., 1926; D и p г ё, ThOorie mOcanique de la chaleur P., 1869; Weber R. u. Gans R., Repertorium d. Physik, В. 1, T. 2, p. 1—123, Lpz.—B., 1916; Neumann Fr., Vor-lesungen liber d. Theorie d. Kapillaritat, Lpz., 1894; G ο n у &., ТЬёопе thermodynamique de la capillarity et de l’dlectrooapillaritd, «Journal de Physique», Paris, 1901, sdrie 3, t. 10, p. 245; Langmuir J., «Journ. of the Amer. Chern. Soc.», 4^rashington, 1917, y. 39, p. 1848—1906; Frumkin A., «Ztschr. f. physikali-sche Chemie», Lpz., 1922, B. 103, p. 5o, 1924, B. 109, p. 34, 1924, B. Ill, p. 190, 1925, B. 116, p. 485, 1926, B. 123, p. 321; Frumkin A., «Ztschr. f. Physik», B., 1926, p. 792; «Ergebnisse d. exakten Naturwissen-schaften, B., 1928, B. 7, p. 235; Rehbinder P., «Ztschr. f. physikalische Chemie», Lpz., 1924, B. Ill, p. 447, 1926, B. 121, p. 103, 1927, B. 129, p. 163, 1929, B. 142, p. 282; Rehbinder P., «Physik. Ztschr.», Leipzig, 1926, p. 825; Sementschenko W., «Zeitschrift fiir physikalische Chemie», Lpz., 1927, B. 129, p. 178. П. Ребиндер.