> Техника, страница 51 > Картографические проекции

Картографические проекции

Картографические проекции, условные построения для изображения сферич. поверхности земли на плоскости. Т. к. сферич. поверхность земли не принадлежит к числу поверхностей, развертывающихся на плоскости, как, например, поверхности конические или цилиндрические, то такие изображения возможны только при допущении известных искажений истинных очертаний или площадей. Чтобы ослабить, насколько возможно, эти погрешности и подчинить их каким-либо законам, прибегают к построениям т. н. картографии, проекций, то есть сначала вычисляют, а затем наносят на бумагу особую сетку меридианов и параллелей, к-рую и заполняют картография. материалом. При этом масштаб, говоря вообще, в различных местах изображения оказывается неизбежно разным, но эти перемены масштаба происходят постепенно, по известным законам, и в более совершенных проекциях они незначительны. При составлении карт можно избегнуть того или иного искажения, для чего следует лишь выбрать соответствующую проекцию, т. к. в каждой проекции преследуется одно какое-нибудь условие в ущерб остальным. Масштаб на проекции различен не только в разных точках, но он меняется и по разным направлениям из одной и той же точки и, в зависимости от свойств проекции, меняется различно. Обыкновенно вдоль одной или нескольких линий (преимущественно меридианов или параллелей) сохраняется наперед заданный масштаб, к-рый называется главны м; по всем же прочим направлениям масштабы будут крупнее или мельче главного; их называют частными;т.о., масштаб карты—величина переменная, и. эти переменные масштабы обладают свойством: сумма квадратов масштабов по двум взаимно перпендикулярн. направлениям— величина постоянная. При всякой проекции в каждой точке сферы существуют два взаимно перпендикулярных направления, по которым частный масштаб будет иметь наибольшее и наименьшее значения (главные направления); на карте они изобра зятся также взаимно перпендикулярными линиями. Главные направления вообще не совпадают с направлениями меридианов и параллелей, за исключением тех проекций, на которых меридианы и параллели пересекаются под прямыми углами.

Все существующие проекции по свойству изображения и по способу построения подразделяются на различные виды. По свойству изображений проекции бывают: 1) конформные, или равноугольные (автогониче-ские), 2) эквивалентные, или равновеликие, и 3) произвольные. На ко и формных проекциях сохраняется подобие очертаний контуров, но в разных местах проекций масштаб будет различный.Равные между собою кружки, взятые в разных точках земной поверхности, на проекции изобразятся также кружками, но радиусы их в разных местах проекции будут различные. В эквивалент-н ы х проекциях частные масштабы по разным направлениям различны, но средняя величина масштаба во всех местах проекции постоянна, то есть эти проекции сохраняют равенство площадей. Каждый кружок, находящийся на поверхности земли, изобразится на проекции равновеликим ему эллипсом (подобие фигур здесь не сохраняется). Произвольные проекции не сохраняют ни подобия контуров ни равенства площадей, но удобны для решения практических вопросов (простота построения). По способу построения проекции делятся на: 1) перспективные, 2) зенитальные, 3) цилиндрические,

4) конические, 5) поликонические, 6) многогранные, 7) условные. Те из перечисленных проекций, при которых контуры непосредственно проектируются на картинную плоскость, называются азимутальны-м и, так как в них каждая точка карты имеет тот же азимут относительно среднего меридиана, что и на земном сфероиде.

I. Перспективные проекции. В этих проекциях контуры земной поверхности изображаются так, как они представлялись бы в перспективе на картинной плоскости. Картинная плоскость располагается перпендикулярно к оптич. оси проекции, то есть к линии, соединяющей точку зрения с центром земли. В перспективных проекциях изображаются очень большие части земной поверхности (целое полушарие), поэтому масштаб для них берут мелкий и землю принимают за правильный шар с радиусом R =а где а—большая полуось, е—эксцентриситет земли. Перспективные проекции делятся на: 1) ортограф и ческ не, когда точка зрения удалена от поверхности земли на бесконечное расстояние, 2)стереогра-ф и ч е с к и е—точка зрения лежит на поверхности земли, 3) центральны е— точка зрения в центре земли, 4) вне ш-н и е—точка зрения вне земли, но на конечном расстоянии. Смотря по тому, пересекает ли оптич. ось проекции земную поверхность в полюсе, на экваторе или под промежуточной широтой, эти проекции бывают: п о-лярные, экваториальные и горизонт и ы е.

Ортографические проекции не сохраняют ни подобия фигур ни равенства площадей; частные масштабы меняются от 1 (в центре карты) до 0 (у краев). В полярной ортографическ. проекции (фигура 1) картинная плоскость совпадает с плоскостью экватора, меридианы на ней изображаются прямыми линиями, пересекающимися в центре карты под углами, равными разностям их долгот, а параллели—концентрич. кругами. В экваториальной проекции (фигура 2) картинная плоскость совпадает с плоскостью какого-нибудь меридиана; меридианы представляются эллипсами, имеющими общую ось, равную диаметру земли, а малые оси их равны 2J2 sin. Я, где Я—долгота данного меридиана; параллели же изображаются параллельными прямыми, отстоящими от центра проекции на величины R sin φ, где ψ—широта данной параллели. В горизонтной проекции (фигура 3) картинная плоскость проходит через центр земли параллельно горизонту любой данной точки; меридианы и параллели изображаются эллипсами, кроме меридиана центральной точки, к-рый будет прямою линиею. Ор-тографич. проекции пригодны для изображения небольших частей земной поверхности; для целого же полушария они применяются в картах луны.

Стереографические проекции сохраняют подобие очертаний контуров. Частные масштабы в них меняются от ^х/₂ (в центре) карты до 1 (у краев). В полярной проекции (фигура 4) картинная плоскость лежит в плоскости экватора; меридианы в ней изображаются прямыми, пересекающимися в центре под углами, равными разностям их долгот, а параллели—концентр ич. кругами. В экваториальной проекции (фигура 5) картинная плоскость совпадает с плоскостью какого-либо меридиана; меридианы и параллели получаются в виде дуг неконцен-трич. кругов, за исключением среднего меридиана и экватора, которые представлены двумя взаимно перпендикулярными диаметрами. В горизонтной проекции (фигура 6) картинная плоскость проходит через центр земли, параллельно горизонту данной точки; меридианы и параллели выражаются кругами. Стереография. проекции применяются для изображения целых полушарий:восточного и западного или северного и южного; отдельные страны изображаются в них весьма редко. Они также применяются для графич. решения многих астрономия, задач.

Центральные проекции. Точка зрения помещается в центре земного шара, а картинная плоскость проводится касательною к поверхности земли. Они не сохраняют ни подобия очертаний ни равенства площадей. Частные масштабы меняются от 1 (в центре проекции) до бесконечности (на краях), поэтому целого полушария изобразить в них нельзя. В полярной проекции (фигура 7) картинная плоскость касательна к одному из полюсов; меридианы получаются в виде прямых, расходящихся из центра под углами, равными разностям их долгот; параллели же—в виде концентрич. кругов. В экваториальной проекции (фигура 8) картинная плоскость касается какой-нибудь точки на экваторе; средний меридиан и экватор изобразятся двумя взаимно перпендикулярными прямыми линиями; все прочие меридиа-

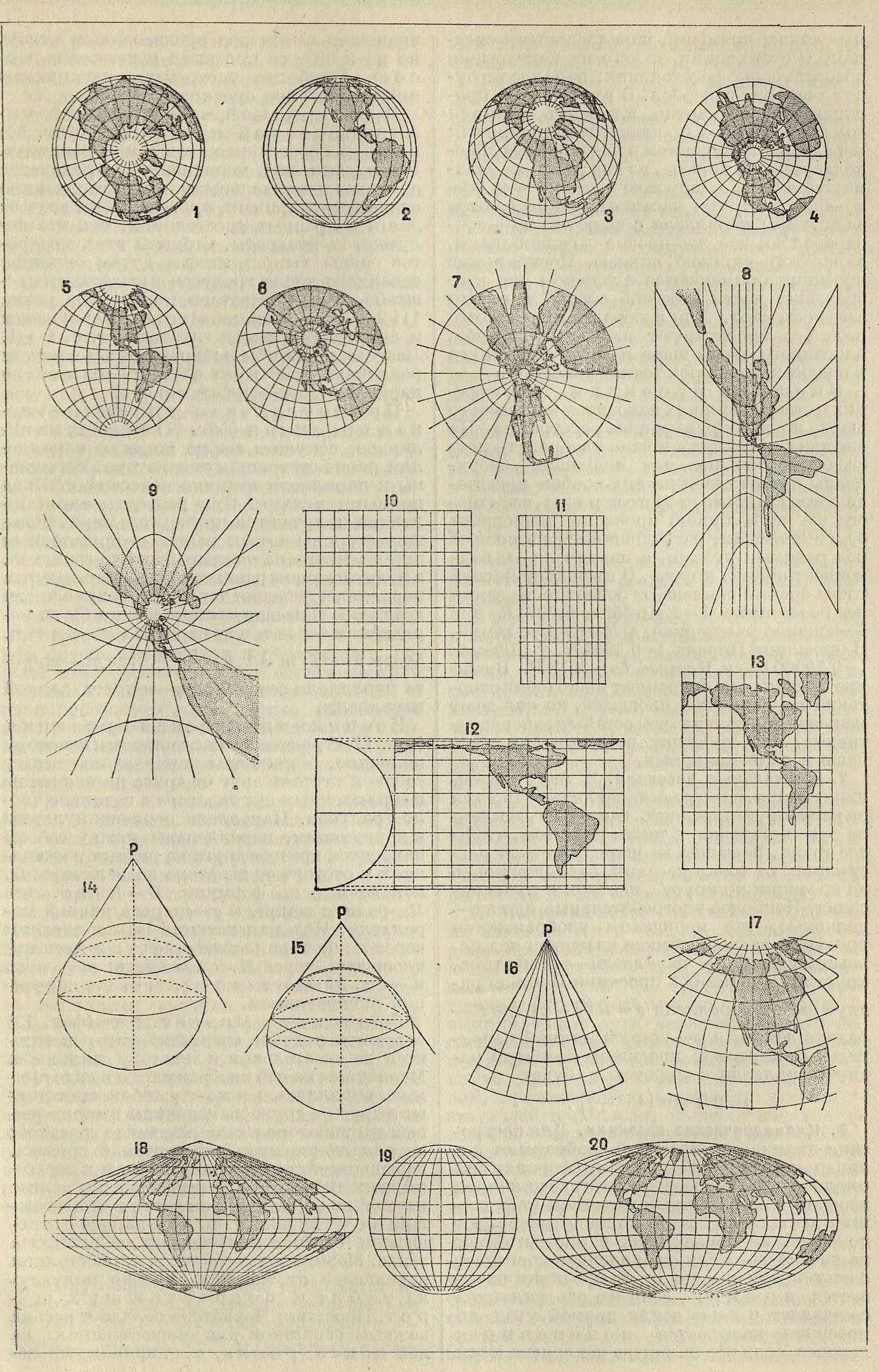
ны—также прямыми, параллельными среднему и отстоящими от него на непрерывно возрастающих расстояниях; параллели будут иметь вид гипербол. В горизонтной проекции (фигура 9) картин, плоскость касается данной точки под промежуточной широтой; меридианы получаются в виде прямых, расходящихся из полюса, но под разными углами; параллели с широтою >, чем 90°— <р₀ (где φ₀—широта точки касания), изображаются эллипсами; параллели с широтою 90°— φ_α— параболою, все же прочие — гиперболами, а экватор—прямою линиею. Центральные проекции применяются с успехом для изображения части небесной сферы, то есть для звездных карт. Для изображения же всего неба его проектируют на 6 граней куба, описанного около шара и касающегося его в полюсах и четырех точках экватора.

Внешние проекции. Точка зрения в этих проекциях находится вне земного шара, но на определенном расстоянии. На внешних проекциях можно изобразить пространство большее, чем полушарие. Меридианы и параллели на них вообще представляются кривыми второго порядка, в частности же на полярной проекции меридианы будут прямыми, расходящимися из полюса под равными углами, а параллели—в виде концентрическ. кругов. В проекции Лагира точка зрения удалена от поверхности земли на расстояние i=_Rsin45°=0,70711£, где I—искомое расстояние, a R—радиус земли. В проекции Парана 1=0,5944R, у Джемса 1=0,50000R, у Кларка 1=0,3676R. Внешние проекции не сохраняют ни подобия очертаний ни равенства площадей, но они дают меньшие искажения, чем остальные перспективные. Эти проекции применяются всего чаще в виде полярных.

2. Звиитальные проекции. В этих проек циях сферич. поверхность земли переносится на картинную плоскость, касательную к земле в данной точке, с таким расчетом, чтобы все точки, лежащие на шаре в равных расстояниях от точки касания, располондались на проекции по кругу с центром в точке касания. Наиболее употребительные из них— полярные, где меридианы изображаются прямыми, расходящимися из центра под равными углами, а параллели—концентрич. кругами. В полярной проекции Постеля радиус любой параллели ρ=R, где R—

радиус земли, а φ—широта данной параллели. В полярной проекции Ламберта радиус параллели с широтою ψ будет

ρ =2Д sin (45°-^).

3. Цилиндрические проекции. Для построения цилиндрич. проекций воображают цилиндр, касательный к земному сфероиду или секущий его. На поверхность этого цилиндра переносят по известным правилам меридианы и параллели, затем цилиндр разрезают по одной из образующих и развертывают на плоскость. Если ось цилиндра совпадает с осью вращения земли, то проекция называется прямою, если же ось цилиндра составляет с осью земли прямой угол, то проекция называется поперечною; наконец, если ось цилиндра наклонена к оси вращения земли под произвольным углом, но не в 90°, то проекция называется косою. Наиболее употребительны прямые цилиндрические проекции.

В к в а д р а-т н о й, или плоской, цилиндрической проекции (фигура 10) цилиндр берется касательным к экватору. Все параллели и меридианы изображаются прямыми параллельными линиями, взаимно перпендикулярными, проведенными друг от друга на равных расстояниях, так что получаются квадраты. Стороны этих квадратов равны выпрямленным дугам экватора заданного числа градусов в заданном масштабе. Дуга 1° экватора, по Бесселю, равна 111 308,42 метров Масштаб т по всем меридианам и по экватору равен главному, то есть т=1. Частные масштабы п по разным параллелям различны, т. e. п =sc φ (где п—масштаб по параллели, а φ—широта ее).

Прямоугольная цилиндрическая проекция (фигура 11) строится на цилиндре, секущем землю по двум параллелям, равно отстоящим от экватора. Меридианы и параллели взаимно пересекаются под прямыми углами. При развертывании цилиндра получаются прямоугольники, большие стороны которых равны выпрямленным дугам меридиана в заданное число градусов, а малые стороны равны выпрямленным дугам параллелей сечения также в заданное число градусов. Называя частные масштабы по меридианам через т, а по параллелям—через и,

будем иметь: т=1, п=^с°^ > где Ψο—широта параллели сечения, а φ—широта данной параллели.

Изоцилиндрическаяпроекция (фигура 12) строится на касательном к экватору цилиндре. Меридианы параллельны между собою и отстоят друг от друга на величины выпрямленных дуг экватора в заданное число градусов. Параллели перпендикулярны к меридианам, параллельны между собою, находятся друг от друга на разных расстояниях и отстоят от экватора на величины D, получаемые из формулы D=Rsinq>, где R—радиус земли, а φ—широта данной параллели.” Называя масштаб по меридианам через т, по параллелям—через п и масштаб площадей—через М, будем иметь: т=cos φ, п =sc φ, Μ=cos ψ sc<p=1, τ. е. эта проекция равновеликая.

Проекция Меркатора (фигура 13) сохраняет подобие очертаний фигур и строится на касательном к экватору цилиндре. Меридианы на ней изображаются в виде прямых, параллельных между собою и отстоящих друг от друга на величины выпрямленных дуг экватора в заданное число градусов;. параллели же проводятся в виде прямых, перпендикулярных к меридианам и пересекающих их т. о., чтобы отношение дуг долгот каждой из параллелей на карте к прилегающим им дугам широт было одинаково с отношением соответствующих им величин на земле. Меридианные части, то есть расстояния параллелей от экватора, удобно получать из таблиц возрастающих широт. Проекция Меркатора обладает весьма важным свойством для мореплавания: на ней локсодромия, то есть кривая, прове-

денная на земном сфероиде так, что она пересекает все меридианы под одним и тем нее углом, изображается прямою линиею.

Квадратная цилиндрич. проекция применяется только для изображения экваториальных стран; прямоугольная—для изображения небольшой по широте страны, причем за параллель сечения берется средняя параллель страны; изоцилиндрическая—для статистических карт; проекция Меркатора— для изображения всего земного шара, кроме полярных стран, на одном листе бумаги и для морских карт.

4. Конические проекции. Они применяются для изображения отдельных вытянутых по долготе стран и основаны на развертывании конуса, для чего воображают конус, касательный к параллели, проходящей через середину страны (фигура 14), или конус, секущий сферу по двум данным параллелям (фигура 15). Ось конуса в большинстве случаев совпадает с осью земли. Меридианы в конич. проекциях изображают в виде системы прямых, расходящихся из общей точки Р (полюса проекции) под равными углами (5, которые называются углами сближения меридианов и, если землю принимают за правильный шар, вычисляются по формуле <5 =Я sin φ₀, где Я—разность долгот, а φ„·— широта средней параллели, если же принимают в расчет сфероидальный вид земли, то 5= Я· а, где а—коэффициент, определяемый условиями проекции в каждом отдельном случае. Параллели изображаются дугами концентрич. кругов с общим центром в полюсе Р проекции. Эти проекции м. б. равнопромежуточными, когда расстояния между параллелями одинаковы, равноугольными и равновеликими. Частные масштабы в них изменяются различно, в зависимости от свойств проекции.

Простая коническая проекция (фигура 16) строится на касательном конусе. Из полюса проекции Р проводят меридианы в виде прямых, расходящихся под углами сближения меридианов; затем у того же полюса проводят параллель касания радиусом g₀ — R ctg φ„, где φ₀—широта параллели касания, a R—радиус земли. Для получения остальных параллелей проводят из полюса дуги радиусами ρ=Β [ctg φ₀ — (φ — <Ρο)]> где φ—широта данной параллели, φ₀—широта параллели касания и разность ψ—ψ₀должен быть выражена в частях радиуса. Масштаб сохраняется по всем меридианам и параллели касания.

Проекция на секущем конусе. Здесь вместо касательного конуса берется конус, пересекающий земной шар по двум данным параллелям, по которым и сохраняется главный масштаб. Называя радиус южной параллели сечения с широтою φ₁ через о_г и радиус северной параллели сечения с широтою ψ₂ через ρ₂, будем иметь;

e i =

R СОЗ Ψχ

. φ* + φ*

ρ₂=o₁—2R sin -

Промежуточные параллели проводятся на равных расстояниях между параллелями сечения. Угол сближения меридианов <5 =

= Я sin <р₀, где <р₀=^φ^^φ Из коническ. проек ций заслуживают внимания следующие: Де-лиля, Эйлера, Альберса, Мердока, Гаусса.

Проекция Гаусса является наиболее совершенной из всех конических и относится к конформным. Эта проекция имеет 5 частных случаев в зависимости от того, где желают сохранить главный масштаб, и в связи с этим м. б. построена либо на касательном либо на секущем конусе. Сетка в ней похояса на сетку всякой другой конич. проекции, только расстояния между параллелями, начиная от наименьшего у средней параллели, непрерывно увеличиваются к северу и югу. При составлении карт в крупном масштабе прибегают к построению проекции по точкам, для чего вычисляют прямоугольные координаты всех точек пересечений меридианов с параллелями, причем эти координаты вычисляют последовательно для каждой широты и за начала координат принимают точки пересечений среднего меридиана с соответствующими параллелями. Осями Х-ов будут служить перпендикуляры, восставленные к среднему меридиану в точках пересечений его с параллелями, а общей осью Г-ов—средний меридиан карты. В этом случае х=ρ sin пд,у= 2ρ sin² у,

где ρ—радиус параллели на проекции и пд—угол между средним и данным меридианами.

Проекция Бонна, хотя и относится к коническим, но представляет условное построение, т. ι-с. меридианы в ней не прямые линии, а кривые—выпуклые наружу. Для построения параллелей чертят систему дуг концентрич. кругов, как и в простой конической (фигура 17); затем на каждой из этих дуг, начиная от среднего меридиана, изо-браясагощегося прямой линией, откладывают истинные длины дуг параллелей в главном масштабе. Меридианы получаются проведением ломаных или непрерывных кривых линий через точки· отложений на параллелях. Эта проекция равновелика, и главный масштаб сохраняется по всем параллелям и по среднему меридиану.

5. Поликонические проекции. Сущность их заключается в том, что около земного шара предполагается не один, а несколько конусов, касательных ко всем изобраяше-мым параллелям. На прямой линии, изображающей средний меридиан, откладывают выпрямленные дуги меридиана меяеду последовательными параллелями и через каждую полученную т. о. точку проводят дугу круга, радиус которого равен длине касательной, проведенной к меридиану у соответствующей параллели, от точки касания до встречи с продолженною осью земли. Т.о., параллели будут дугами эксцентрич. кругов, и расстояния между ними по мере удаления от среднего меридиана увеличиваются. Радиус ρ любой параллели с широтою φ выражается формулой: д=R ctg φ, где R— радиус земли. Меридианы строятся так же, как и в проекции Бонна. Искажения в этих проекциях возрастают по мере удаления от среднего меридиана. Они не сохраняют ни подобия контуров ни равенства площадей и употребляются для стран, растянутых по широте. При известных условиях эти про екции можно сделать также равноугольными или равновеликими.

6. Многогранный проекции. Для построения этих проекций предполагают весьземной сфероид разбитым меридианами и параллелями на ряд сферическ. трапеций и, принимая каждую из них за плоскость, изображают на отдельном листе бумаги. Если такие трапеции складывать вместе по параллелям, то получатся просветы по меридианам; при соединении же их боками получаются просветы по параллелям. При сложении десяти листов вместе эти просветы еще незначительны. Многогранные проекции можно применять двумя способами: 1) проектировать каждую сферич. трапецию на секущую площадь, проходящую через вершины углов этой трапеции, или 2) переносить каждую сферич. трапецию на поверхность касательного конуса, а затем развернуть конус на плоскость. Первым способом строят рамки съемочных планшетов. Многогранные проекции, представляя собою отдельные листы, применяются при составлении карт крупных масштабов до 1:1 000 000 вкл. Они лучше всех др. проекций сохраняют подобие очертаний контуров и равенство площадей.

7. Условные (произвольные) проекции. К этому типу относятся все те проекции, построение которых делается иными, чем перечисленные, приемами.

Синусоидальную проекцию Сан-сон а можно отнести к цилиндрическим. Для ее построения на прямой, изображающей средний меридиан страны, откладывают выпрямленные дуги меридианов между последовательными параллелями и через полученные точки проводят прямые, перпендикулярные к среднему меридиану; они представят параллели, на каждой из которых откладывают в обе стороны, от 0 до 180° в каждую, части, равные дугам соответствующих параллелей. Ломаные или непрерывные кривые, получаемые соединением соответствующих точек на параллелях, дадут изображения меридианов. Если в этой проекции построить всю земную поверхность, то получится фигура, на которой меридианы изобразятся изогнутыми кривыми—синусоидами (фигура 18). Эта проекция относится к эквивалентным.

Гомолографическая проекция Мольвейде (фигура 19) принадлежит к равновеликим и строится так: чертят окружность произвольного радиуса и проводят два взаимно перпендикулярных диаметра; горизонтальный диаметр, изображающий экватор, делят на несколько равных частей и затем строят эллипсы, проходящие через точки деления и концы вертикального диаметра (среднего меридиана),— эти эллипсы будут меридианами. Для получения параллелей проводят прямые, параллельные экватору, с таким расчетом, чтобы площадь каждого отдельного четыреугольника равнялась соответствующему четыреугольнику на земле. Если на линии, изображающей экватор, отложить вдвое более этих частей, а средний меридиан оставить без перемен и через полученные точки провести новые эллипсы, то в этой проекции изобразится на одном эллипсе весь земной шар.

Проекция Айтова служит для изображения всей земной поверхности на одном эллипсе (фигура 20). Экватор и меридианы в этой проекции строятся подобно тому, как и в гомолографической. Для получения изображений параллелей делят все уже проведенные эллиптические меридианы на равные части и через полученные точки деления проводят непрерывные кривые, причем экватор выразится прямою линиею.

Лит.: В и т к о в с к и и В. В., Картография, СПБ, 1907; его же, Топография, М., 1928; Шокальский Ю. М., О международной карте в масштабе 1:1 000 000, П., 1923; Пенк А., О составлении и издании карты всей земной поверхности в масштабе 1:1 000 000, пер. с нем., «Изв. Русского географии, общества», СПБ, 1892, т. 24, стр. 435; Т и с с о А., Изображение одной поверхности па другой и составление географии, карт, пер. с Франц., М., 1899; Моррисон, Как построить географ, карту и как ей пользоваться, М., 1907; Красовский Ф. Н., Новые картографические проекции, Москва, 1922; В e e t г С. Н. a. Adams О. S„ Elements of Map Projection, Wsh., 1921. В. Никифоров.