> Техника, страница 51 > Катушки самоиндукции

Катушки самоиндукции

Катушки самоиндукции, устройства или приборы, имеющие при сравнительно небольших своих размерах и занимаемых пространствах большие величины к о э-фициентов самоиндукции (смотрите Индуктивность) и состоящие обычно из провода, намотанного для компактности в виде катушек различного вида и формы, откуда и происходит их название.

Классификация К.с. В радиотехнике К.с. находят применение: 1) в колебательных контурах—для настройки последних на определенные частоты, 2) в устройствах связи (смотрите Катушки связи) колебательных и вообще электрич. контуров и цепей, 3) в отдельных цепях—для защиты (дросселирования) этих цепей от воздействия на них токов определенных частот.

В зависимости от назначения К. с. изменяются характер их устройства и размеры, причем как то, так и другое в сильной степени зависит от силы циркулирующего в них тока. В связи с этим К. с., применяемые в радиотехнике, делятся на два следующих основных вида: 1) К. с., предназначенные для передатчиков, и 2) К. с. для приемников. К. с. передатчиков имеют обыкновенно большие геометрическ. размеры и наматываются из голого провода (полого или ленточного) больших сечений. В виду больших напряжений, развиваемых в К. с., применяется хорошая изоляция между витками, а также между намоткой и землей; обычно намотка имеет большой шаг и витки крепятся к каркасу при помощи фарфоровых изоляторов. В этой категории К. с. электрически первостепенную роль играет уменьшение до минимума активных потерь, для чего провод часто серебрят или (при коротких волнах) золотят. Основное отличительное свойство приемных К. с.— компактность, которая однако должна достигаться при возможно меньшем сопротивлении потерь, почему чрезвычайно важное значение приобретает вопрос о наивыгоднейшем диаметре провода для намотки К. с. различных форм. Намотка производится обычно из изолированного (шелком, хл.-бум. оплеткой или эмалью) провода и накладывается на изоляционные каркасы, изготовляемые из эбонита, картона, папье-маше и тому подобное. материалов с небольшой диэлектрической прочностью. В целях придания обмотке механич. прочности и жесткости допускается склеивание ее при помощи шеллака, коллодия и тому подобное. быстро застывающих и склеивающих изоляционных составов.

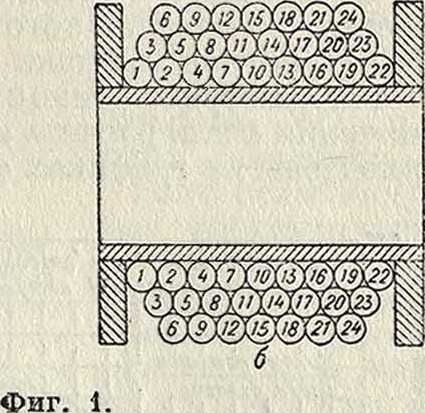
Основными формами К. с., которые находят наибольшее распространение в радиотехнике, являются следующие. 1) Цилиндрические или соленоидальные К. с.: а) однослойные, наматываемые на цилиндры, изготовляемые из изоляционных материалов; б) многослойные с намоткой или слой за слоем (фигура 1, а) или в перекидку; при намотке в перекидку (фигура 1, б) катушка наматывается всеми своими слоями сразу от одного конца ее к другому. Разновидностями цилиндрич. К. с. являются катушки с сечением в виде многоугольника. 2) Плоские К. с.: а) галеты—многослойные, обычно цилиндрич. катушки, длина которых весьма мала по сравнению с толщиной намотки; б) спиральные, наматываемые из круглого провода или из ленты в один слой. 3) Сотовые К. с.—многослойн. катушки, намотка которых производится зигзагообразно (фигура 2)

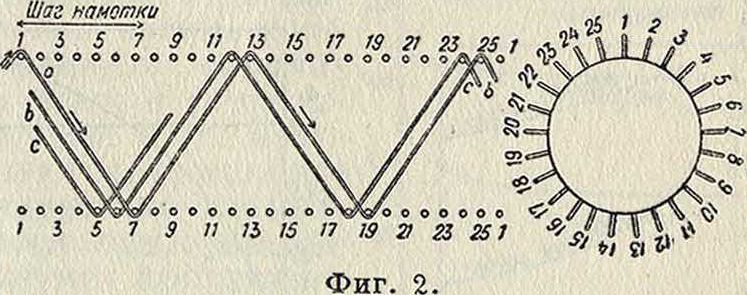
между двумя рядами спиц (с нечетным числом их), расположенных радиально на одинаковых расстояниях друг от друга по поверхности цилиндрич. формы и удаляемых для снятия катушки с каркаса после окончания намотки. Шаг намотки сотовых катушек (фигура 2) м. б. взят любым, при обязательном условии—чтобы частное от деления полного числа спиц без одной в одном ряду на шаг обмотки давало четное число. 4) Корзинчатые К. с.: а) цилиндрич. катушки наматываются между спицами, расположенными по окружности и как бы образующими цилиндр (фигура 3), причем число спиц

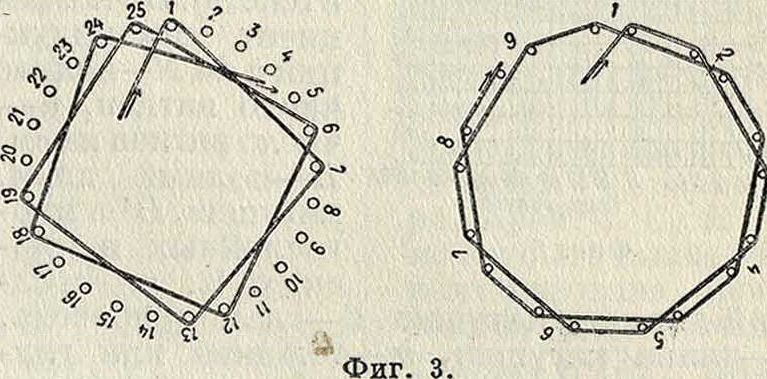
и самый порядок намотки м. б. самым разнообразным; на фигуре 3 для примера показаны два вида такой намотки; б) радиальные катушки, намотка которых кладется на спицы через одну или две, причем спицы расположены на поверхности цилиндрич. каркаса радиально в один ряд, или в радиальные вырезы, сделанные в специальном каркасе, отштампованном или вырезанном из картона или тонкого листового эбонита. 5) Тороидальные К. с.—с намоткой, заполняющей тороид (кольцо) с сечением в виде круга или квадрата. 6) Восьмерочные: а) однослойные, наматываемые на два цилиндра, расположенные рядом и имеющие оси параллельными; б) многослойные, состоящие из двух галет, расположенных для образования восьмерки рядом и имеющих намотку в противоположных направлениях. Тороидальные К. с. замечательны тем, что они не имеют внешнего магнитного поля; восьмерочные же К. с. имеют его сильно ослабленным.

Электрич. свойства К. с. характеризуются: 1) коэф-том самоиндукции L, 2) сопротивлением R при рабочей частоте тока или просто отношением L:R, которое является постоянной времени К. с. Иногда К. с. характеризуется также углом потерь <5, определяемым из ур-ия:

tg<5=-^- ·

В приемной радиотехнике оказывается весьма рациональным характеризовать К. с. отношением (oL :R =π:δ, к-рое является мерой чувствительности и избирательности (смотрите) того контура, в к-ром участвует данная К. с. к

Ί 25

Коэф-т самоиндукции К. с так же как и сопротивление, изменяется в зависимости от частоты циркулирующего в ней тока.

Формулы для расчета L К. с. Для токов очень низкой частоты (постоянных токов) L м. б. определен по приводимым ниже формулам. в которых приняты следующие общие обозначения (если иные не оговорены в тексте): L—коэфи-циент самоиндукции в cm,N—полное число витков, п— число витков на см, D—полный диам. катушки, D в многослойных и плоских К. с.—средний диаметр катушки, d—диаметр провода, Ϊ—длина катушки, т—толщина или глубина намотки катушки, b — шаг намотки (расстояние между осями проводов).

Цилиндрическая однослойная К. с. из круглого провода:

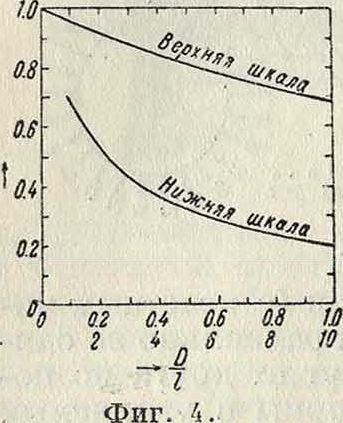
L=^k=π² D- - и² · ϊ · к (ф-ла Нагаока),

где к—фактор, учитывающий форму катушки,· зависит от отношения Ώ : Ϊ; его значения можно определить из графика фигура 4; π D N=w—полная длина провода катушки, следовательно

L=~r · к.

Число вилимо Фигура 6.

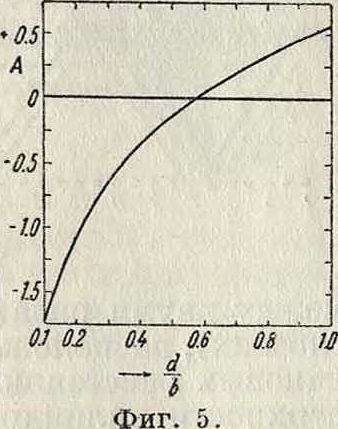
В случае, если между витками провода значительное расстояние (изоляция или обмотка;· имеет шаг), для точного подсчета L необходимо ввести поправочный член AL== 2π D Ν(Α + В), где А и В—постоянные,

dN

зависящие: первая—от отношения —, а вторая—от числа витков N. Значения А и В даны на графиках фигура 5 и 6. Для окончательного определения коэф-та самоиндукции· 1/₀ катушки, поправочный коэф-т AL нужно вычесть из значения, полученного по основной формуле Нагаока: L₀=L— ΔL; ΔΗ изменяет величину L относительно 1₀ при учете изоляции для сплошной обмотки не больше, чем на 1—2%, так что в этом случае поправкой можно практически пренебречь. Для расчета цилиндрических К. с. общеупотребительна, особенно в электротехнике, формула Эмде [Ц

Многослойная К. с:

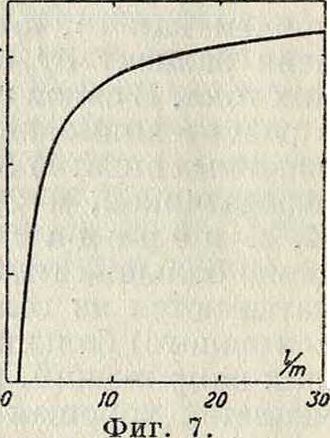
_Ll=В - ²ⁿ-^Nii^D-^m (0,693 + Е),

где Е—постоянная, зависящая от отношения I : m (значения ее е определяются из графика фигура 7), и L— °·³ коэф. самоиндукции, вычисленный по формуле Нагаока. Эта формула для °·² длинных катушек дает результаты с точностью до 0,1%; при op

^ ^ 0,25 и~^5 точность ее уменьшается.

Поправка на изоляцию или шаг в обмотке определяется из следующего уравнения:

L₀=Li + 2л D N (in -f 0,155).

Для расчета многослойных К. с. может быть применена формула Нагаока в ее простейшем виде. В этом случае фактор к зависит не только от отношения 1: D, но и от отношения

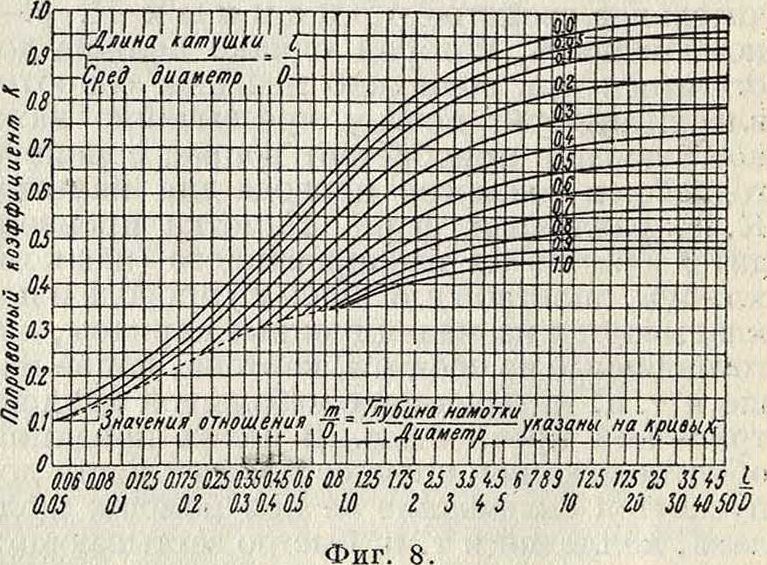
m: D, причем к с увеличением т : V уменьшается, вследствие того что поле от внутренних витков катушки целиком не связывается непосредственное внешними витками. Значения к для расчета многослойных К. с. приведены на графиках фигура 8 и 9.

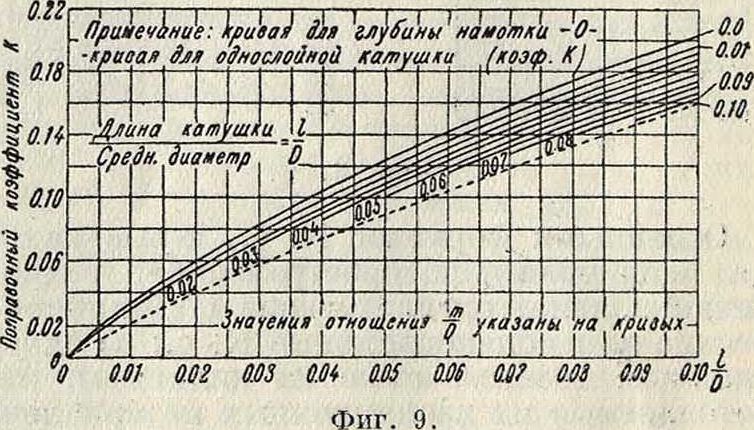
Плоские К. с; L плоских К. с. га летного типа может рассчитываться по тем же ф-лам, что и многослойных К. с.· При 1< т

молено пользоваться также следующей ф-лой:

В=2 π· D ·Ν* [(l

+

где C=ΫΙ² + m² (ф-ла Стефана), a F и G показаны на графиках фигура 10. Спиральные К. с. из круглого провода рассчитываются по формуле:

L-2».D.№[ln^— ! + (lnf + |)],

где m=N b, a D= а + (п — 1)b; значения « и b см. на фигуре 11.

Спиральные К. с. из проводника прямоугольного сечения (ленты) м. б. рассчитаны по формуле Стефана для плоских галет (смотрите выше), где I—уже толщина ленты. Плоские,

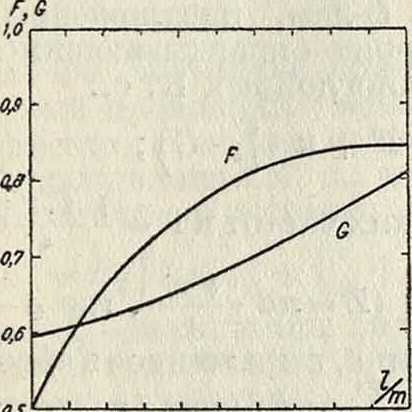
0 0,1 0,2 0,3 0,4 0.5 0,0 0,7 00 00 1.0

Фигура 10.

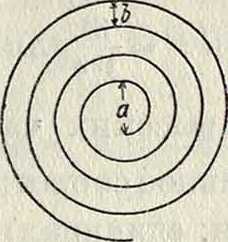
Фигура 11.

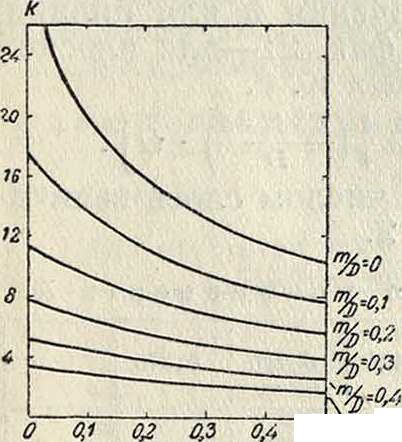
Фигура 1Z.

а также и цилиндрические К. с., могут быть рассчитаны по упрощенной формуле, предложенной впервые проф. Шпильрейном [*]: L=N* D к,

где к определяется по графику фигура 12.

Сотовые и корзинчатые К. с. рассчитываются лишь с нек-рым приближением по ф-лам цилиндрических, многослойных и плоских К. с.

Тороидальные К. с. рассчитываются по формуле:

L=2л N² (А - УЖ-Щ, где Δ—диам. тороида между центрами его сечений, a D—диам. намотки.

Восьмерочные К. с. рассчитываются как цилиндрические или многослойные, в зависимости от вида катушки, с учетом коэфициента взаимоиндукции между катушками, образующими восьмерку.

Расчет самоиндукции многоугольных К. с. может быть приведен к расчету эквивалентной цилиндрической К. с., если ~о/^гц₎.о,5 воспользоваться по-% правочными коэфи-циентами — (Гровера), данными на фигуре 13. Для определения L нужно вычислить l:D₁ и из графиков найти соответствующую величину Ό : D_lt где D₁— диам. описанного круга. Отеюдадупределяет-

к рас-ррения азра-, при счеты ся D, и дальше все чету цилиндрически: и упрощения техни ботан целый ряд та! помощи которых BQe

£

^y—Восьмиугольник

ЦШестиугольна“

Л

0) 02 Ofi 0,4 0,S 0,0 <v RO 00 u>

Фигура 13.

L К. с. могут быть произведены в несколько минут с точностью до 5—10% и большей, что для практических целей б. ч. достаточно.

Величины С, λ₀ и В для К. с. Сопротивление К. с. для постоянного тока и очень низких частот определяется активным сопротивлением (постоян- I ному току) прово- * да, из которого она намотана. При высоких частотах ко-

эфициент самоин- —.__

дукции И сопроти- -Квадрат вление К. с. изменяются, причем это ^0,7 изменение вызывается одновременно °·¹ двумя причинами: собственной емко- « стью катушек и вихревыми токами.

1) Собственна я, или распределенная, емкость К. с. для удобства расчетов м. б. представлена в виде нек-рого конденсатора, шунтирующего катушку и эквивалентного суммарному емкостному эффекту между отдельными витками. Величина собственной емкости С₀ К. с. обычно невелика. В случае однослойной К. с. она не зависит от числа витков и лишь в незначительной степени зависит от отношения длины к диаметру. При ϊ=0,5 D величина С₀приблизительно равна 0,54г (г—радиус катушки).При l=2Dona равна 0,57г (Гоу) или также приблизительно равна 7% периметра (Брейт). С₀ К. с. может быть также охарактеризована собственной длиной волны λ„=2π Vl G_a. Величина К. с. (в ж) определяется из уравнения А₀=2Ы (Дру-Фигура 14. де), где к—фактор, за висящий от отношения I : Ь и b : d (фигура 14). С₀ однослойных К. с. обычно не превышает 10 сантиметров и равна нормально 3—5 см; С₀ цилиндрич. корзинок— порядка 2 см; чительно выше и достигает 30 — 40 см.

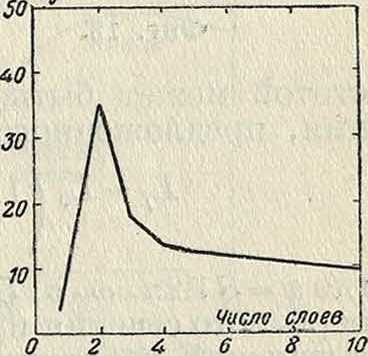
Наибольшую С₀ имеет двуслойная К. с.; при увеличении числа слоев С₀ уменьшается. На фигуре 15 показаны кривые зависимости С₀ от числа слоев для катушки, у которой D =

= 3,8 см, 1=8 см, N (в слое)=58 виткам.

ЕМКОСТЬ К. С. ВЫЗЫ- Фигура 15.

вает при увеличении

С₀ многослойных К. с. зна-

частоты увеличение действующих L и 1?,. При рабочих длинах волн, близких к Я₀, действующий L определяется из уравнения:

1 — ю“ · 1,₀ С,

— Д) (1 + ^ω~ l₀ Со);

действующее R определяется из уравнения

D ___й.___ й₀ ^

^а· (1 - о>^г · L, с„)^{2 —} и - я;/д«)· =

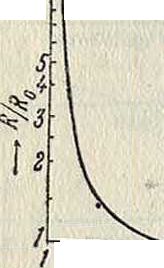
- Л₀ (1 + 2со² · Х₀ · С„), где L₀ и Д_ч—значения при постоянном токе. Таким образ, сопротивление увеличивается с частотой быстрее, чем L. На фигуре 16 покажи зана зависимость R : R₀ от λ : λ₀.

Неудовлетворительнаяизоляция намотки К. с., являющейся диэлектриком для емкости между витками, вызывает дополнительные, т. н. диэлектрические, потери К. с. Проводимость утечки изоляции G уве-гщ ю личивает сопротивление К. с. на величину ΔД_д.=ω² · L² · G; так

Фиг 16 ^{как G=й, С}° ^t8^{0> то}

Δ RI=со“ · Ώ- С„ · tg <3, где tg(5—угол потерь, вызываемый емкостью К. с. Для наиболее распространенных видов изоляции проволок, применяемых для намотки К. с., tgd имеет следующие величины: эмаль—0,018, шеллак—0,04, хл.-бум. изоляция—0,36 (по Штреккеру). Склеивающие катушку составы вызывают обычно дополнительные диэлектрические потери. На фигуре 17 показаны кривые зависимости R от f для одинаковых К. с., но покрытых различными составами. Ко-эфициент самоиндукции—L при диэлектрической утечкеоста-ется в первом приближении неизменным.

2) Вихревые токи (токи Фуко). Магнитное поле токов, протекающих в других витках К. с., приводит к аксиальной несимметричности тока в проводнике данного витка, что в свою очередь вызывает увеличение сопротивления R катушки, значительно большее возрастания сопротивления от скин-эффекта в прямом проводе. В то же время вихревые токи вызывают уменьшение Lс увеличением частоты. Это уменьшение !у с частотой может быть определено из уравнения, предложенного Зоммерфельдом:

i - Ψ (ж)

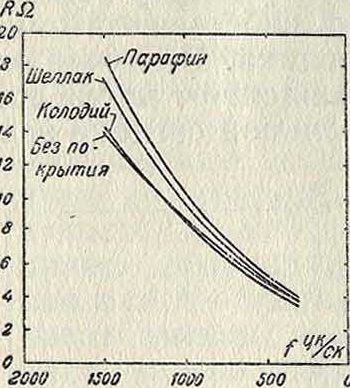
Фигура 17.

Lf=L₀

1 -

1-Д·

У

нием L, вызываемым собственной емкостью К. с. На фигуре 19 показаны кривые зависимости L от /, измеренные для наиболее рас-, пространениых при-

—-емных К. с. Из этих кривых видно, что уменьшение L с частотой от вихревых токов значительно меньше по абсолютной величине, чем see то то"" увеличение L от ем-. _{фиг 19} кости, поэтому прак тически К. с. дают обычно увеличение Lf. Сопротивление К. с., вызываемое потерями в проводе, м. б. рассчитано по следующим ф-лам, предложенным Вёттеруортсом и хорошо оправдывающимся на практике. Для однослойных К. с.:

Сотовая

Ш J

УдКорзинпа радиальная

Однослойная

Rf=R₀(l+F + и ~ · gJ ;

здесь F=— для низких частот и F =

V 2-Z+1

для высоких частот (Z

, Vv *

,_πα. —L, _Где ρ—

удельное сопротивление, выраженное в абсолюта. единицах), G=~- для низких частот и

G

61

V 2 -Z-1

¹—g— для высоких частот, и — зависит от размеров катушки. В табл. 1 даны значения 1 + Р и G для меди (ρ=1700).

Таблица 1.—Значения 1+F и G для мед!

	Z	1+F	G	Z	1+F	G	Z	1+F	G
	од	1	Z4	4	1,678	0,5842	15	5,562	2,525
	0,5	1	0,00097	4,5	1,863	0.669	20	7.328	3,409
	1	1,005	0,01519	5	2,043	0,755	30	10,86	5,177
	1,5	1,026	0,0691	6	2.394	0.932	40	14,40	6,946
	2	1,078	0,1724	7	2,743	1,109	50	17,93	8,713
	2,5	1,175	0,2949	8	3,094	1,287	80	28,54	14,02
	3	1,318	0,4049	9	3,446	1,464	100	35.61	17,55
	3,5	1,492	0,4987	10	3,799	1,641	>100	1/2Z+1	^2·Ζ-1
								4	8

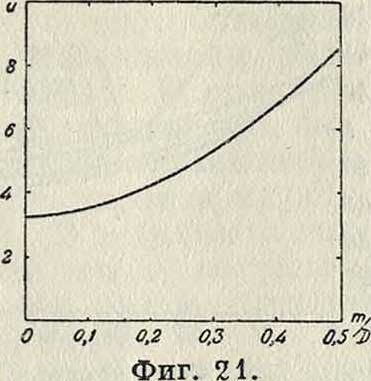
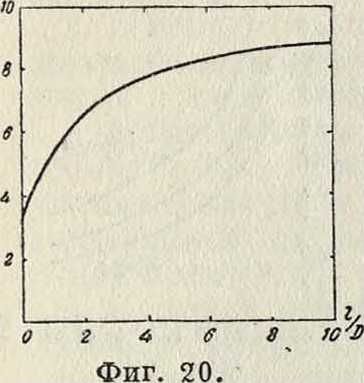
На фигуре 20 даны значения и для цилиндрических К. с., а на фигуре 21—для плоских К. с. Для многослойных К. с.

R_f=R₀[l+F + {(*A^Y-G].

Для К. с. с большим числом слоев величины К даны в таблице 2.

Т а б л. 2,—3 н а ч е н и я коэфициента К.

где х=£ ω a, S—сторона квадрата по перечного сечения провода, γ—фактор, учитывающий изоляцию и поправку на круглый провод; обычно у=1,25.

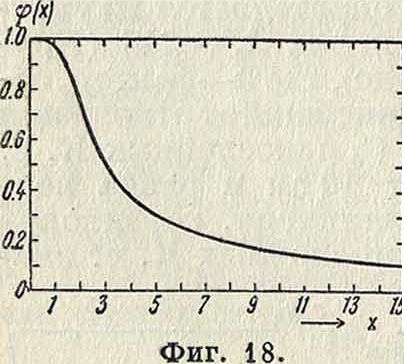
ч „sh2x-sin2x ¥>(»)- /2 * ch2x -соь2ж

Кривая зависимости φ(χ) от х показана на фигуре 18. Уменьшение L с частотой от вихревых токов обычно компенсируется увеличе

1: D т:	0,000	0,125	0,250	0,375	0,5
0,0	со	41,7	21,2	14,4	11,0
0,1	52,4	23,3	15,4	11,6	9.5
0,2	27,4	16,2	12,4	9,9	8,2
0,3	19,6	13,7	10,7	8,8	7,5
0,4	16,0	12,0	9,5	8,0	6,9
0,5	13,8	10,4	8,4	7,0	6,0

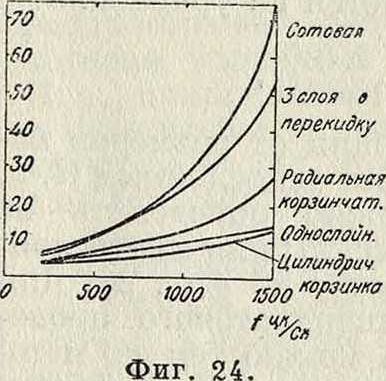
на фигура 22 и 23 показаны К для цилиндрич. и плоских К. с. в один и два слоя, а также при бесконечном числе слоев. На фигуре 24 показаны кривые R в зависимости от f для тех же приемных К. с., для которых на фигуре 19 дана была зависимость L от f.

Для уменьшения сопротивления К. с. применяют т. н. лицендратовый проводник, состоящий из многих изолированных друг от друга жил, скрученных т. о., что каждая жила лежит частью внутри кабеля, частью

на его наружной поверхности. Лицендратовый проводник уменьшает влияние скин-эффекта с последующим уменьшением R_f. Сопротивление К. с., намотанных из лицен-дратового проводника, определяется ур-ием:

%=B₀[l+F + g; + -J-^)n^.G],

где d₀—диам. жилы лицендрата, а п₀—число жил в нем. Фактор к зависит от п₀; его значения следующие:

тг„. 3 9 27 Большое к. 1,55 1,84 1,92 2

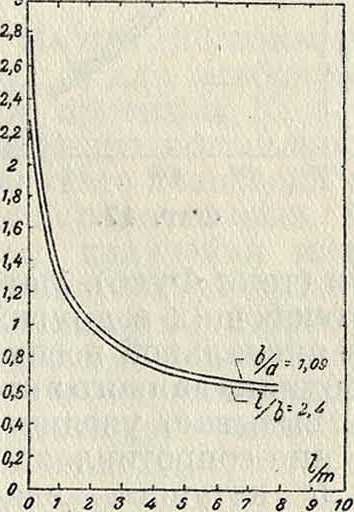
В табл. 3 показана величина a>L : R для катушек (D=8,3 см, 1=1,5 cjvi, т=3 см), •намотанных сплошным и лицендратовым изменениях. Оптимальная длина К. с. определяется шагом намотки. Наилучший шаг намотки в свою очередь определяется из соотношения: ^=/(Z), где Z=(Д₀—

1 R₀ · λ

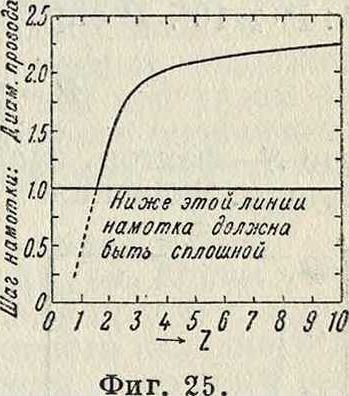
сопротивление постоянному току 1 км дан-ного провода; Λ—в м). Кривая зависимости ^ от Ζ, построенная Бёттеруортсом, показана на фигуре 25. При отклонении на 20% шага намотки от значения, указываемого этой кривой, R : L увеличивается приблизительно на 5%. Для средних частот Ζ <2 и отношение l:D д. 6.5:0,35; для высоких частот Z > 2 и отношение l :D ^ 0,3. В случае многослойных К. с. оптимальное I: т для низких частот должен быть порядка 1, для высоких частот—порядка 0,3—0,5. В тороидальных К. с. для получения минимального R : L отношение внешних и внутренних радиусов тороида г₂ : ту=2,66.

KJ2

Л

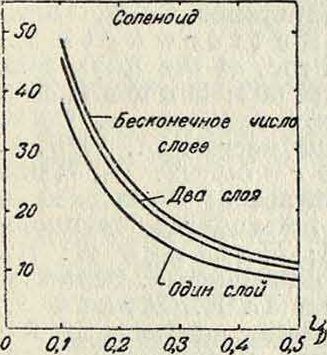
Фигура 22.

λг

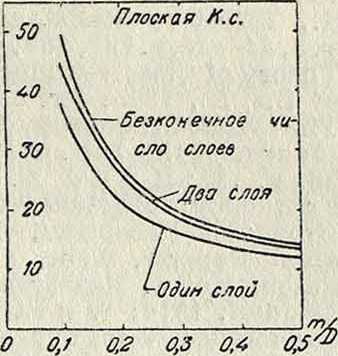
Фигура 23.

проводниками: при очень высоких частотах лицендратовый проводник теряет свое значение вследствие возрастания диэлектрических потерь между жилами.

Таблица 3. — Значения величины o>L R.

При L (в см) » Я (в м)		(при конденсаторе С=450 см)	73 362	343 786	2 170 1 970
! 1		1) для сплошного проводника	133	116	108
т 1		2) для лицен-дратового проводника	192	203	224

Наилучшие размеры К. с. К. с. действует тем лучше, чем меньше R_f при данном L_f, то есть чем меньше R : L или R : ыЬ. Хорошо сконструированная К. с. для передатчика должна иметь R : coL^ 0,002; у приемной

К. с. R : coL < 0,01-^-0,005; R:L обратно пропорционально D. Самая форма К. с. при этом оказывает очень малое влияние на отношение R: L, даже при ее значительных

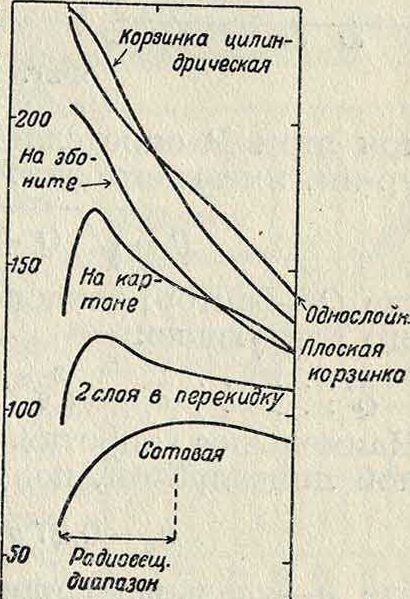
На фигуре 26 показано изменение величины coi,: R для наиболее распространенных видов приемных К. с. (фигура 19 и 24). Кривые наглядно показывают, что для радиовещательного диапазона наилучшими К. с. являются однослойные. В случае длинных волн для получения минимальных R : L однослойные К. с. пришлось бы строить с очень большим D. Поэто-„. му, в целях компакт- ™ ности,в приемниках применяют многослойные К. с.; в диапазонах волн 1 000 3 000 метров применяются сотовые К. с., на волнах более высоких—галеты. В передатчиках на всех волнах рационально применять лишь однослойные К. с., что вполне осуществимо, т. к. L К. с. в передатчиках дляданных волн невелика, в виду больших емкостей контурных конденсаторов.

При конструировании приемных К. с.⁰ гм мо woo ^Кт-вопросом громадной фигура 26.

важности является выбор наивыгоднейшего диаметра провода катушки для получения минимального R : L. Для однослойных и многослойных К. с. наивыгоднейший диам. провода d определяется из уравнения, устанавливающего

следующую функциональную зависимость: Р d — q>(f : Р²).

Значения Р d в зависимости от : Р² могут быть определены из табл. 4.

Таблица 4. —График для определения наилучшего диаметра провода К. е.

f	Р2	Р d	t :	P2	Ρ · d
1	10*	0,920	1	• ΙΟ6	0,230
2	10*	0,730	2	• ίο*	0,211
4	ю4	0,585	4	10*	0,195
6	104	0,512	6	• 10β	0,190
8	ю4	0,468	8	• 10β	0,185
10	ю4	0,435	10	• 10β	0,181
20	ю4	0,354	20	• 10*	0,179
40	104	0,290	40	• 10*	0,175
60	ю4	0,262	60	10*	0,173
100	104	0,230	100	• 10«	0,171

а“=при f : Р² < 10⁴ и и=~⁵- при /:Р²5=10⁸. Р определяется из уравнения:

’ =

L S® ЮООШ

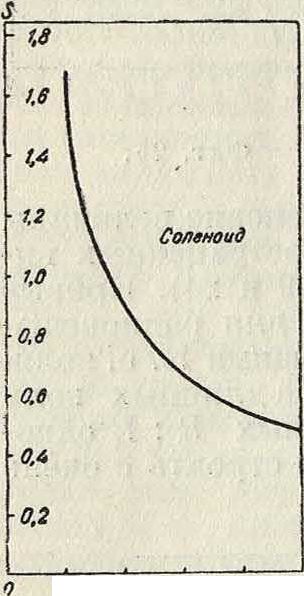
где S—фактор, зависящий от размеров катушки. Значения его для однослойных К. с. можно определить из фигура 27; для многослойных— из фигура 28. Для лицеидратового провода можно тем же методом определить наивыгоднейший диам. жилы;

0,1 0,2 0,3 0,4 0.5

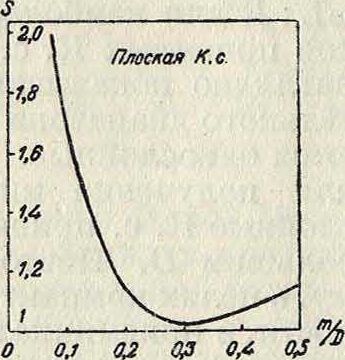
Фигура 27.

при этом Р определяется уже из другого ур-ия, имеющего вид:

e+w-

где Q—фактор, зависящий от п_сг Значения его следующие:

п,.1 3 9 37 Больше

Q.О 0,9 3,3 10,4 0,4п„

Наименьшее сопротивление К. с., намотанной лицендратом, получается при п₀=0,27 ρ >

где ρ—удельное сопротивление материала (в и к—фактор, зависящий от разме ров катушки и провода (величина его определяется из графика фигура 29).

В условиях практики приходится иногда решать следующие задачи при конструировании К. с.: 1) построить наилучшую катушку для данного веса меди; теория показывает, что наилучшей катушкой в этом случае является однослойная при 1 В=⁴/з> плоская при т : D — ¹/_i и многослойная, у которой 5т+31=Н; 2) построить катушку для определенной общей поверхности; в этом случае I : .0=0,375; но в виду резкости изменения вблизи минимума R : L можно

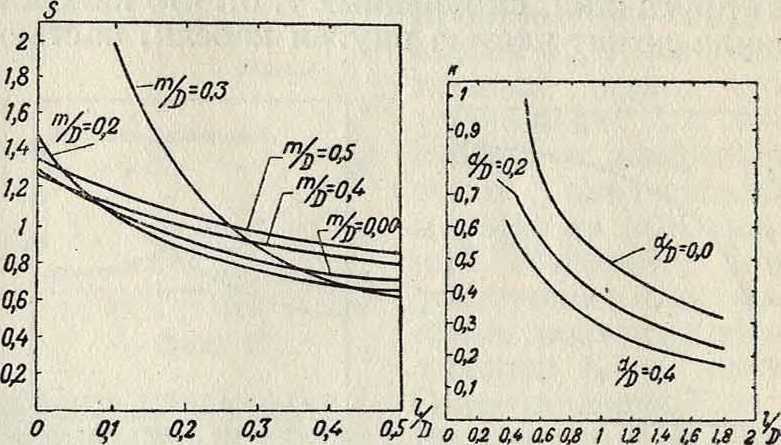
Фигура 28.

Фигура 29.

считать, что и в данном случае действуют те же условия оптимальности, что и в первом случае.

Лит.: ’) Ernie F., Zur Berechnung eisenfreier Drosselspulen ftir Starkstrom, «EuM», 1912, p. 221; ^!) 8 p i e 1 r e i n J., Die Induktivitat eisenfreier Кr,::i-singspulen, «Archiv filr Elektroteclmik», Berlin, 1915, B. 3, H. 7. — Рейнер, Справочник по радиотехнике, пер. с англ., М., 1929; Ббттеруорте С., Расчет катушек самоиндукции с низкими потерями, Ленинград, 1928; Виккер Д. А., «ТиТбП», 1922, 12; Крылов Η. Н., там же, 1928, т. 9, 49; But-terworth S., The Design of Inductance Coils having a Rectangular Winding Section, «Experimental Wireless», London, 1925, v. 2, 24, p. 750; Grover 1*’., «Bureau of Standards, Scientific Papers», Wsh., 1922, 455; Barton Chappie H., The Self-Capacity of Inductance Coils, «Experimental Wireless», London, 1925, v. 2, 23, p. 716; Sowerby A. L., Inductance Coils Quantitatively Compared, «Experimental Wireless», London, 1926, v. 3, 31, p. 220; Butterworth S., Effective Resistance of Inductance Coils, ibid., v. 3,31—35, p.203, 309, 417, 483; В utterworth S., Theory of Closely-wound Coils, «Proc. of the Royal Soc. of L.», L., 1925, ser. A, v. 107, p. 693; Howe G. W., The High-Frequency Resistance of Wires a. Coils, «Journ. of the Inst, of Electr. Engineers», L., 1920, v. 58, p. 152; H u n d A. a. d e G г о о t Η. B., Radio Frequency Resistance a. Inductance of Coils used in Broadcast Reception, «Bureau of Standards, Technological Papers», Wsh., 1925, 298; Nottage W. H., Calculation a. Measurement of Inductance a. Capacity, London, 1916; Whi 11 em о r e L. E., Breit J., Inductance, Capacity and Resistance of Coils at Radio Frequency, «Physical Review», Minneapolis, 1919, v. 14, p. 170; Breit G., The Effective Capacity of Multilayer Coils with Square and Circular Section, «Philosoph. Magazine», London, 1922, v. 43, 257, p.963; Fortescue C. L., The Design of Inductances for. High-Frequency Circuits, «Journal of the Inst, of Electr.Engineers»,L., 1923, v. 61, p. 133; В r о w n W. a. Love J., Designs a. Elficiencies of Large Air Core Inductances, «Proc. of th ; Inst, of Radio Engineers», N. Y., 1925, v. 13, 6, p. 755; Grover F., Formulas a. Tables lor the Calculation of the Inductance of Coils of Polygonal Form, «Bureau of Standards, Scientific Papers», Washington, 1923, 468; firoverF., A Coin-par,son on the Formulas for the Calculation of the Inductance of Coils and Spirals wound with Wire of Large Cross Section, «Journal of Research», Wsh. 1929, v. 3, 1; E s a u A., Spulen mit nebeneinander liegenden Windungen (Flachspulen), «Jahrb. der draht-losen Telegraphie», Berlin, 1919, B. 14, p. 386; Elct-1 i n R., Ein experimenteller Beitrag zum Spulenpro-blem, «Archiv f. Elektroteclmik», Berlin, 1928, B. 20, H. 5—6, p. 507; S о m m e r f e 1 d A., tlber d. Wech-selstromwlderstand d. Spulen, «Ann. d. Phys.», Lpz., 1907, B. 24, p. 609; Rogowskl W., Die Spule bei Wechselstrom, «Archiv f. Elektroteclmik», Berlin, 1919, B. 7, Ii. 1, p. 17. П. Нуксенио.