 > Техника, страница 52 > Кинематика механизмов
> Техника, страница 52 > Кинематика механизмов
Кинематика механизмов
Кинематика механизмов, наука, занимающаяся изучением кинематич.свойств механизмов. Она тесно связана с теоретич. кинематикой и является приложением ее законов к механизмам. К. м. состоит из учения: 1) о структуре механизмов, 2) о траекториях точек механизма, 3) о методах определения путей, скоростей и ускорений точек механизма и 4) из кинематического исследования передач.
Учение о структуре механизмов охватывает собой вопросы, касающиеся устройства механизмов, то есть звеньев, из которых они состоят, и способов сцепления этих звеньев между собою (кинематическ. пары). Здесь решаются задачи на составление кинематическ. схемы механизма по данной его конструкции, определяется число степеней свободы у кинематическ. цепи, проводится структурный анализ механизмов и излагаются методы синтетич. построения схем новых механизмов по данным условиям. Для решения этих задач применяется преимущественно формальный арифметическ. метод подсчета числа переменных параметров и условий связи, которыми определяется движение механизма.
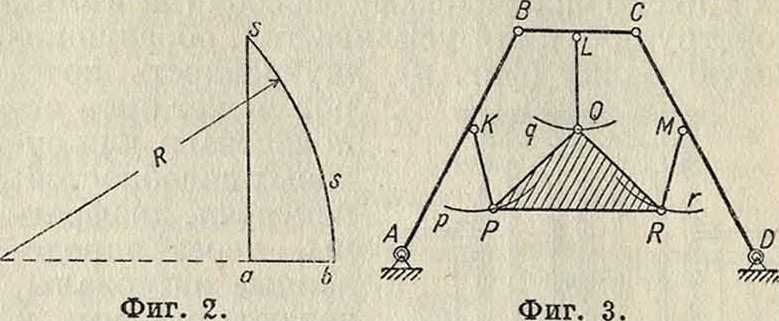
Траектории точек механизмов лишь в редких случаях исследуются аналитическим методом. Объясняется это тем, что у механизмов траектории точек обыкновенно выражаются уравнениями высоких степеней. Уже точка шатуна простого плоского четырехзвенного механизма ABCD описывает кривую 6-го порядка. Для примера на фигура 1 показана одна из многих таких кривых, причем секущая SS, как видно, пересекает траекторию точки М в 6 точках. Если бы был взят механизм посложнее, то порядок кривой траектории получился бы еще выше. Отсюда проистекает большая трудность аналитич.построения уравнений траекторий точек механизмов. Графический метод построения траекторий при помощи простых засечек циркулем дает вполне удовлетворительные результаты. При этом, если для построенной кривой требуется дать уравнение, его составляют приближенно при помощи рядов Фурье, пользуясь для определения коэфи-циентов ряда особым прибором—г а р м о-ническим анализатором (смотрите Гармонический анализ), или же при помощи таблиц Ципперера. Когда перемещения точек очень малы, а в Построении траекторий требуется значительная точность, как например при исследовании парораспределительных механизмов, то пользуются методом круговых линеек, причем схема механизма вычерчивается в небольшом масштабе, траектории Hie точек сносятся к одному месту и выполняются в крупном масштабе. Вместо засечек радиусами больших кругов в этом случае применяются круговые линейки-лекала (фигура 2), у которых ss—дуга круга данного радиуса R, а кромка аb идет по направлению к центру этого круга. Бывают еще
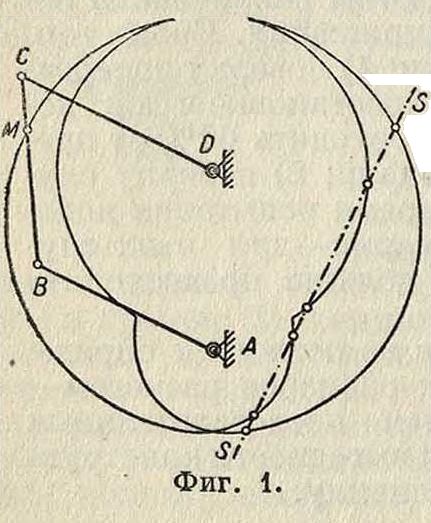
случаи, когда методом простых засечек задача просто не решается и требуется прибегать к сложным геометрич. построениям. Тогда целесообразно применение шаблонов, которые легко вырезаются из картона. На фигуре 3 показана схема механизма ABCD, к к-рому тремя поми КР, LQ и MR присоединено так называемым трехповодковое звено PQR. Если известны все размеры механизма и дана скорость кривошипа АВ, то для каждого положения точки В засечками легко находится соответствующее полозкение точки С, так как ее расстояния от В и D постоянны. Вместе с тем определятся также положения точек К, ЬиМ. Однако дальнейший переход к точкам Р, Q и R затрудняется тем, что для засекания каждой из этих точек нехватает данных. В этом случае целесообразно изготовить шаблон треугольника PQR, прочертить окруяшости р, q и г и затем вместить этот шаблон соответствующими вершинами на указанных окрузкностях. Тогда определится его полозкение, а вместе с тем и полозкение искомых точек Р, Q и R.
Определение путей, скоростей и ускорений точек механизмов производится разными методами — аналитическим, графическим и смешанным (графо-аналитическим). В аналитическом методе нужно установить функциональную зависимость перемещений точки от времени: s=f(t) для линейных перемещений и α=φ(ί) для угловых. Диференцированием получаем следующие скорости:
Соответственно ускорения равны: тангенциальное
dv d‘s. dt " dt‘ ’
нормальное где ρ—радиус кривизны траектории точки; угловое
. da dta ω = dt ~ ~dt‘ ‘
Гораздо чаще применяется графич. метод, состоящий в построении кинематич. диаграмм (графиков): s, i; v, t; j, t. Для построения этих диаграмм сначала строят траекторию точки, затем разбивают ее на интервалы, соответствующие равным промезкуткам времени, промеряют траекторию по этим интер-
валам и составляют первую диаграмму s, ί (фигура 4). Графическим диференцированием с этой диаграммы снимают приращения ds за каждый интервал времени dt. Отношение
= V в выбранном масштабе откладывают в средине интервала как среднюю скорость итак. обр. получают вторую диаграмму v, t.
Из этой второй диаграммы аналогичным способом снимают приращения dv за каждый t интервал времени и составляют третью диаграмму }, t. Нужно заметить, что при криволинейном движении точки мы можем получить описан, методом не полное ускорение точки, а только тангенциальную составляющую его. Во многих случаях этого бывает достаточно. Если же требуется знать полное ускорение по величине и по направлению, то пользуются методом планов скоростей и ускорений. Обратная задача состоит в графическом интегрировании. Она за-
тт ds
ключается в следующем. Из v=dt следует,
V
что s=J v dt. Таким образом путь точки за
О
известный промежуток времени является площадью на графике скоростей за этот промежуток. Измеряя эту площадь, например при помощи планиметра, получим путь s. Этим приемом хорошо пользоваться в том случае, когда скорости двиясения точки заданы, а требуется найти перемещения ее. Подобным же образом из ускорений получаются скоро-
άν 5
-сти; именно: j —, откуда J j dt, и еле-
О
довательно площадь на графике ускорений соответствует скорости точки. Планы скоростей и ускорений строятся графич. приемами на основании геометрич. соотношений, которые устанавливаются между векторами скоростей и ускорений разных точек механизма. Т. к. при построении планов скоростей и ускорений наряду с графич. построениями проделывается значительная вычислительная работа, то метод этот следует считать графо-аналитическим.
Кинематическое исследование передач охватывает собой учение о передачах: фрикционной, зубчатой,” гибкой связью, кулаками и эксцентриками, а также стержневой пространственной и в частности шарниром Гука. У всех этих передач устанавливают отношение скоростей между сцепленными деталями; кроме того находят форму правильно построенных очертаний зубцов зубчатых колес, кулаков и эксцентриков. Обратная задача состоит в том, что по данной форме этих деталей определяют закон движения.
Лит.: Зернов Д. С. Прикладная механика, Л., 1925; Левене он Л. Б., Кинематика механизмов, М., 1923; М е р ц а л о в Н. И., Кинематика механизмов. М., 1916; Р а д ц и г А. А., Прикладная механика, М.—П., 1923; Рузский Д. П., Кинематика машин, Ленинград, 1924; Смирнов Л. П., Кинематика механизмов и машин, М.—Л., 1927; Столяров Я. В. Теория механизмов, Харьков, 1926; Асе у р Л., Исследование плоских стержневых механизмов с точки зрения их структуры и классификации, ч. 1, СПБ, 1914, ч. 2, П., 1915; Малыше в
A. П., Анализ и синтез механизмов с точки зрения их структуры, Томск, 1923; его же, Прикладная механика, вып. 1—Структура и синтез механизмов. Томск, 1923; К и р и и ч е в В. Л., Построение путей, описываемых точками плоского механизма, Собр. сочинений, т. 1, П., 1917; его ж е, Построение картины скоростей и картины ускорений для плоских механизмов, там же; А с су р Л. В., Картины скоростей и ускорений точек плоских механизмов. СПБ, 1911; А л ь б и ц к и и В. И., Цилиндрич. зубчатые колеса, их теория, расчет и вычерчивание, 2 изд., Харьков, 1892; Берлов М. И., Детали машин, Сокращ. руководство по расчету и проектир., ч. 1—2, 2 изд., М., 1929; Малышев А. П„ Передача гибкой связью при некруглых шкивах, «Изв. Моек, текстильного ин-та», М„ 1928; Burmeister L. Lehr-buch d. Kinematik, Lpz., 1888; Boiasse H., Th6o-rie des vecteurs. Cindmatique des mdeanismes, P., 1921; Heck R. C., Mechanics of Machinery. Mechanism, N. Y„ 1923; G г u b 1 e r M., Lehrbuch d. technischen Mechanik.B. 1—3, B., 1921; H a m C. W. a. C r a n e E. J., Mechanics of Machinery, N. Y„ 1927; Eeii-leaux F., Theoretische Kinematik, В. 1, Brschw., 1875, B.2, Brschw., 1900; Grubler M., Getriebelehre,
B., 1921; S t r i b e c k, Versuchemit Schneckengetrie-ben, «Z. d. VDI», 1897; Flanders R., Gear-Cutting Machinery, N. Y., 1910; B u h 1 e, Der Renolds-Ketten-trieb, «Gliiokauf», Essen, 1904; Buckingham E. Spur Gears, N.Y., 1922; Hiscox G., Mechanic. Appliances. Mechanical Movements, 5 ed., L., 1925; Brown H„ Bewegungsmeehanismen, Lpz., 1925. А. Малышев.