> Техника, страница 52 > Кинематический метод

Кинематический метод

Кинематический метод в строительной механике,применение принципа возможных перемещений к решению вопросов теории сооружений; в более узком смысле—применение этого принципа к определению усилий в шарнирно-стержневых фермах от действия неподвижной и подвшк-ной нагрузок. Основная идея К. м., разработанного гл. обр. трудами Мюллера-Вре-слау и Мора, состоит в следующем: путем удаления одной или нескольких связей сооружение обращается в кинематическ. цепь, имеющую одну или несколько степеней изменяемости; искомые свойства сооружения получаются из рассмотрения свойств движения и условий равновесия этой цепи.

В настоящей статье рассматриваются исключительно применения кинематики к плоским сооружениям. Применение кинематики к сооружениям пространственным разработано пока очень мало.

Поверка неизменяемости сооруле ений. Необходимое условие статическ. определимости и неизменяемости сооружения заключается в том, что кинематич. цепь, получаемая из сооружения при удалении каких-либо связей, должна иметь степень свободы, равную числу этих удаленных связей (стержни сооружения считаются абсолютно жесткими). Отсюда выводится соотношение между числом стержней С и числом шарниров Ш шарнирно-стержневой плоской статически определимой и неизменяемой фермы: 2ΠΖ — С=0 (здесь С—полное число стержней, включая и опорные). Отсюда же можно вывести и соотношение между числом звеньев (неизменяемых систем) п и приведенным числом шарниров р любого плоского статически определимого сооружения:

Зп — 2р - 3=0 ;

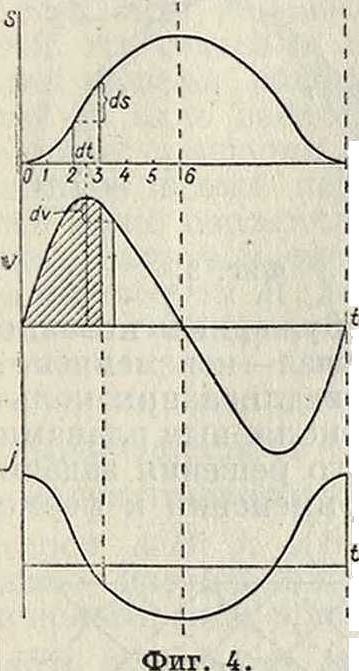
т. э. т. х.

6

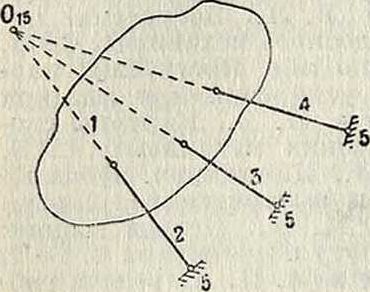
Фигура 1.

приведенное число шарниров получается, если каждый шарнир, соединяющий г звеньев, считать за г —1 простых шарниров.

Всякое сооружение, статически определимое, неизменяемое и неподвижное в общем виде, может, при нек-ром специальном подборе длины стержней, потерять свою неизменяемость или неподвижность, то есть превратиться в кинематич. цепь. Если эта цепь допускает лишь бесконечно малые перемещения, сооружение называется мгновенно изменяемым. Мгновенно изменяемое сооружение непригодно для практ. целей, так как от действия ничтожно малых внешних нагрузок в нем могут возникать большие деформации и большие внутренние усилия. Система уравнений статики, которая служит для определения всех усилий и реакций такого сооружения, имеет детерминант, равный нулю, и поэтому получает решение неопределенное или бесконечное. Мгновенная изменяемость вскрывается проще всего К.м.: нужно удалить одну связь, рассмотреть возможное перемещение полученного механизма и выяснить, противоречит ли удаленная связь этому перемещению; если противоречия нет, то данное сооружение несомненно обладает мгновенной изменяемостью.

На фигуре 1 показана неизменяемая фигура, обозначенная цифрой 1 и опирающаяся на неподвижную систему 5 при помощи опорных стержней 2,3 а и 4. Удалив один из стержней, получим /, мгновенный центр вращения звена 1 в точке пересечения остальных двух 0₁₅; в том случае, когда все три стержня пересекаются в одной точке, движение (бесконечно малый поворот звена 1 вокруг точки 01₆) оказывается возможным и при наличии всех трех опорных стержней. Свойство мгновенной изменяемости сохраняется и в том случае, когда три стержня, пересекающиеся в одной точке, служат для взаимного соединения каких-либо двух неизменяемых частей сооружения, как это изображено например на фигуре 2, где соединительные стержни пересекаются по три: в точках Н и I. Случай параллелизма трех соединительных стержней должен рассматриваться как частный случай пересечения трех стержней в одной точке.

Если какие-либо два звена (обозначим их цифрами 1 я 2) или два стержня соединены между собой шарниром, то разъединив звенья в этом шарнире, получим два механизма и в каждом из них найдем мгновенный центр вращения одного из названных звеньев относительно их общего звена; если шарнир и эти два мгновенных центра лежат на одной прямой, то данное сооружение мгновенно изменяемое. На фигуре 3 точка .А играет роль мгновенного центра 17 (то есть звена 1 относительно звена 7), точка С—центра 27, следовательно сооружение является мгно с

Фигура 2.

венно изменяемым. Из этого примера следует, между прочим, что трехшарнирная арка с шарнирами, расположенными по одной прямой, мгновенно изменяема.

Для раскрытия мгновенной изменяемости пользуются также планами скоростей. Если по удалении какого-либо стержня сооружения можно построить план скоростей (изображающую фигуру), все линии которого параллельны соответствующим стержням данной цепи (в том числе и удаленному стержню), то сооружение мгновенно изменяемое противн. случае—неизменяемо. Теорема одинаково справедлива при пользовании полярным или неполярным планами скоростей. Пример такого решения задачи показан на фигуре 4, в применении к ферме

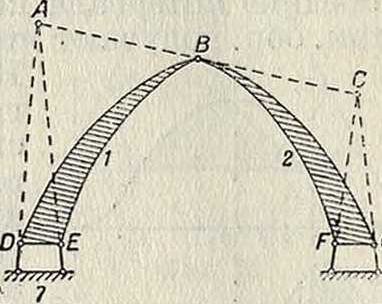
Фигура з.

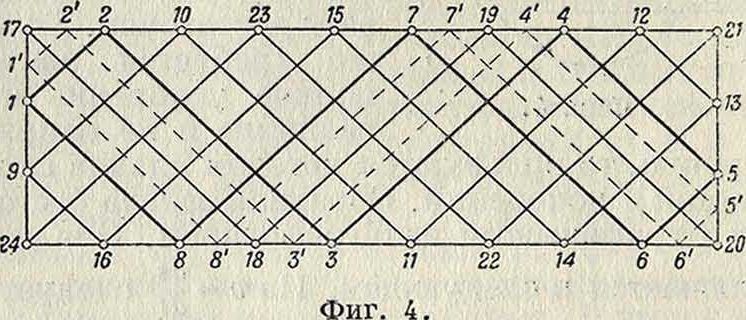
Мертенса, имеющей один лишний стержень и тем не менее мгновенно изменяемой. Пунктирный зигзаг представляет собою неполярный план скоростей и изображает такое перемещение, при котором узлы изображаемого зигзага перемещаются, в то время как остальные узлы остаются неподвижными.

Кинематический способ определения усилий от неподвижной нагрузки представляет собою непосредственное применение статики механизмов и многократно изменяемых кинематич. цепей (то есть цепей с большей степенью свободы, чем у механизма). Основные теоремы статики механизмов, вытекающие из принципа возможных перемещений, наиболее удобно выражаются при помощи полярных и неполярных планов скоростей. На неполяр- _я А ₀

ном плане каждая точ- ⁴| гс г ка А механизма (фигура 5, а) ; !

изображается в виде некоторой точки А, а каждая прямая АВ, не изменяющая своей длины во время движения,— некоторой прямой АВ АВ.

Скорость или перемещение любой точки А выражается в одном и том же (произвольном) масштабе вектором АА; направление перемещения перпендикулярно к этому вектору. При равновесии механизма сумма статических моментов всех внешних сил относительно точек, которые служат изображениями точек приложения соответств. сил, равна нулю. На полярном плане скоростей (или перемещений)

/(-

-ia’

Фиг. откуда изображение а каждой точки А получается (фигура 5, б) как конец вектора ба, проведенного из постоянной точки О—полюса плана скоростей—перпендикулярно к перемещению точки А; свойство параллелизма неизменяемой прямой АВ и ее изображения ab сохраняется и здесь. Условие равновесия механизма: сумма статическ. моментов всех сил, перенесенных на план скоростей, относительно полюса О равна нулю. Иными словами, если мы примем план скоростей за одно звено, имеющее неподвижную точку вращения в полюсе плана и нагруженное всеми перенесенными силами, то это звено окажется в равновесии. Если в числе нагрузок имеется сосредоточенная пара с моментом М, действующая на какое-либо звено АВ (фигура 5, а), то при пользовании неполярным планом нужно ввести в упомянутое выше ур-ие статических моментов выражение М (l > где отношение

^А™ положительно при одинаковом течении векторов АВ и А В и отрицательно при взаимно противоположных направлениях. При пользовании полярным планом следует вводить выражение М причем дробь положительна при одинаковом течении векторов ab и АВ.

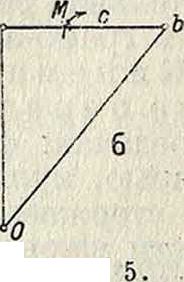
На фигуре 6 показана ферма, для которой обычное построение усилий (без замены стержней) затруднительно. Кинематическое построение состоит в следующем: удаляем стержень CD, заменяем его двумя равными

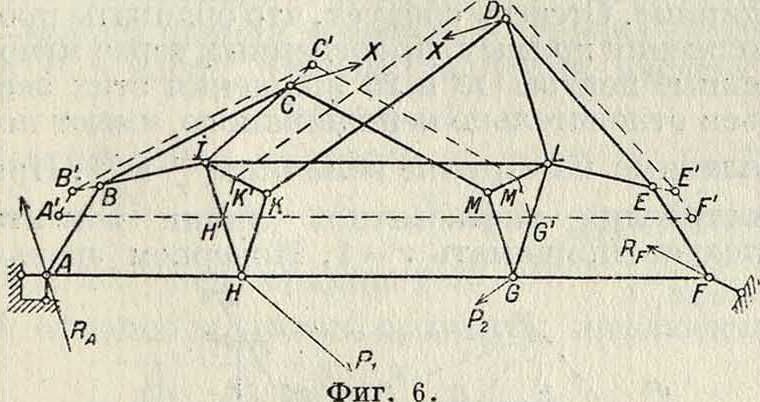
и противоположными силами×и строим неполярный план скоростей, приняв за неподвижное звено стержень IL. Ур-ие равновесия будет иметь вид:

Piкц + P^kp-l· +Д^,/Ср+

-j- Хк@ -Ь Xhj) ~ 0,

где к_н—плечо силы Р_г относительно точки Л и т. д. и где сумма моментов берется конечно алгебраически. После того как сила×будет найдена, усилия во всех остальных стержнях легко найдутся обычным путем.

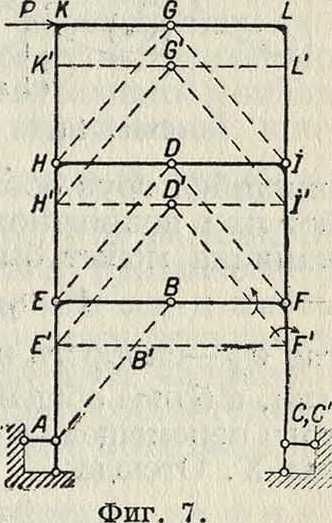
На фигуре 7 изображена трехъярусная рама, состоящая из трех шарнирных арок, поставленных одна на другую. Требуется определить изгибающий момент в сечении F от действия горизонтальной силы. Вставим в сечении F звена ВС шарнир, превращающий полуарку BFC в два звена, и нагрузим это сечение двумя моментами, равными М. Построив неполярный план скоростей, показанный пунктиром, получим:

м=

Р KE’

F’C BF

FC BF

На фигуре 8 показан полярный план для того же механизма; он состоит из одного тр-ка, так как в одной вершине сливается изображение многих точек. Уравнение равновесия имеет вид:

P-Of

_ь/__/С

BF FC

Кроме механизмов можно пользоваться также двукратно изменяемыми кинематич. цепями, основываясь на следующих свойствах таких цепей: 1) при всевозможных бес-крнечно малых перемещениях цепи геометр. местом мгновенных центров взаимного вращения каких-либо двух звеньев служит прямая;

2) если в системе, имеющей две степени свободы, задано направление скорости какой-нибудь точки А, то, при возможных перемещениях этой системы, изображения всех ее точек на полярном и неполярном планах скоростей перемещаются по прямым линиям. Удалив из сооружения две связи, рассматривают два различных возможных перемещения получен, цепи, строят для каждой из них план скоростей и приходят к вышеуказанным уравнениям равновесия. Из этих двух уравнений и определяются усилия в обеих устраненных связях. Легко подобрать два таких движения, при которых в каждом уравнении остается лишь по одному неизвестному.Пользование двукратно изменяемой цепью оказывает большие услуги при решении особо сложных по своей геометрической структуре сооружений. Тот же принцип приводит к пользованию многократно изменяемыми кинематическ.цепями, то есть цепями, обладающими п степенями свободы, где п> 2. Нужно лишь, чтобы п возможных перемещений, для которых строятся планы скоростей и применяются уравнения равновесия, были все независимыми друг от друга (то есть чтобы ни одно из них не было линейной функцией остальных).

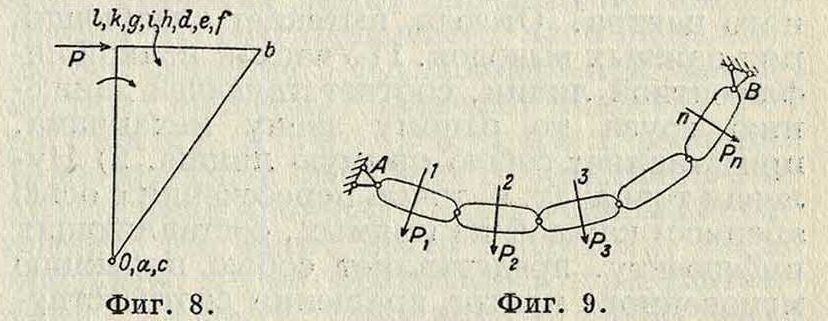
Частным случаем многократно изменяемой кинематической цепи является в е р е-вочный многоугольник, теория которого общеизвестна. Обобщением веревочного мн-ка является дисковый многоугольник (фигура 9), состоящий из звеньев, нагруженных между шарнирами. Для его равновесия необходимо и достаточно, чтобы существовал веревочный мн-к, соответствующий данной внешней нагрузке и обладающий тем свойством, что его стороны проходят через соответствующие вершины дискового мн-ка. Теория равновесия замкнутого дискового к о л ь-ц а автоматически вытекает из теории равновесия дискового многоугольника как ее частный случай.

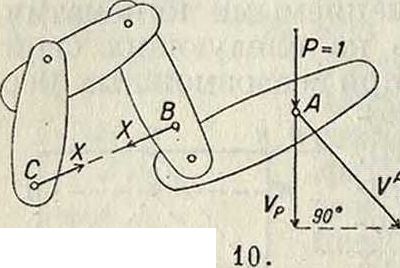
Построение линий влияния (инфлюентная линия). Пусть требуется определитьли-ншо влияния усилия×в каком-нибудь стержне или связи фермы. Удалим этот стержень и заменим его силами X, как показано на фигуре 10; движущийся груз обозначим через Р. Ур-ие работ при возможном перемещении этого механизма может быть представлено в виде: 1 · V р — Xv_x — 0,

где v_x—скорость изменения расстояния СВ или, в более общей формулировке, скорость того перемещения, на котором работают силы X. Отсюда:

У=—·

v_x

Фиг.

Знаменатель этой дроби, как скорость определенной точки или группы точек сооружения, можно считать постоянным, числитель же, по самой природе своей,—переменный. Полученная формула приводит к следующему замечательному выводу: для получения ин-флюентной линии усилия любой связи статически определимой фермы следует удалить эту связь, сообщить образовавшемуся механизму бесконечно малое перемещение и для всех точек сооружения, по которым должна перемещаться точка приложения груза Р =1, построить проекции скоростей на направление, параллельное этому грузу; полученная диаграмма скоростей и будет выражать собою в некотором масштабе искомую инфлюенту.

При бесконечно малом перемещении механизма каждое звено его поворачивается около своего мгновенного центра вращения, а скорость любой точки звена пропорциональна ее расстоянию до этого мгновенного центра. Отсюда вытекает следующий ряд важных выводов. 1) Участок всякой ин-флюентной линии, соответствующей движению груза по одному звену механизма, представляет собою прямую линию. 2) Нулевая точка (то есть точка пересечения с осью абсцисс) каждой из прямых, составляющих инфлюенту, представляет собою проекцию мгновенного центра вращения соответствующего звена по направлению движущейся силы. 3) Точка пересечения двух прямых инфлюенты представляет собою проекцию мгновенного центра взаимн. вращения соответствующих двух звеньев; если последние движутся друг относительно друга поступательно, то обе прямые оказываются параллельными между собою. 4) Если ось абсцисс инфлгоентной линииперпендикуляр-на к направлению проекций v_p, то тангенс угла наклона любой прямой к оси абсцисс выражает собою в выбранном масштабе угловую скорость вращения соответствующего звена относительно неподвижного; этот угол следовательно не зависит от направления ординат Vp.

Эти основные теоремы вполне достаточны для построения любой статически определимой инфлюентной линии. Они же позволяют с недостижимой для друг, методов наглядностью сразу, без каких-либо предварительных вычислений, представить себе весь характер и очертание инфлюентной линии, а также проверять результаты построений, сделанных друг, способами .Масштаб ординат инфлюерты показан на фигуре 11. Для определения усилия в стержне АВ, соединяющем два звена, находим мгновенный центр 0₁₂ взаимного вращения этих звеньев и опускаем из него перпендикуляр г на стержень АВ; любая ордината d, заключенная между прямыми 1 и 2, выражает собою проекцию v_P относительной скорости под грузом и следовательно выражается формулой d=; на расстоянии г от

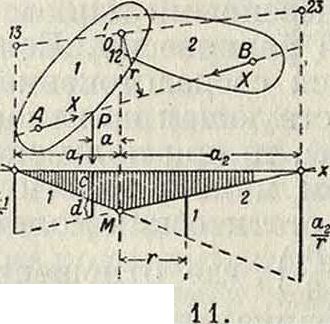
Фиг. точки М инфлюентной линии отрезок ординаты между прямыми 1и2 должен быть равен единице. Отсюда следует, что ординаты продолжения прямых, проведенных через мгновенные центры 13 и 23 вращения этих звеньев относительно неподвижного, имеют по казанные на чертеже величины и ~. При построении инфлюентной линии момента следует принимать г=1. Повернем звенья

1 и 2 на фигуре 11 так, чтобы сила Р, стоящая в какой-либо точке, совершила положительную работу. Если при этом расстояние АВ увеличится, то ордината под этой точкой положительна—таково правило знаков.

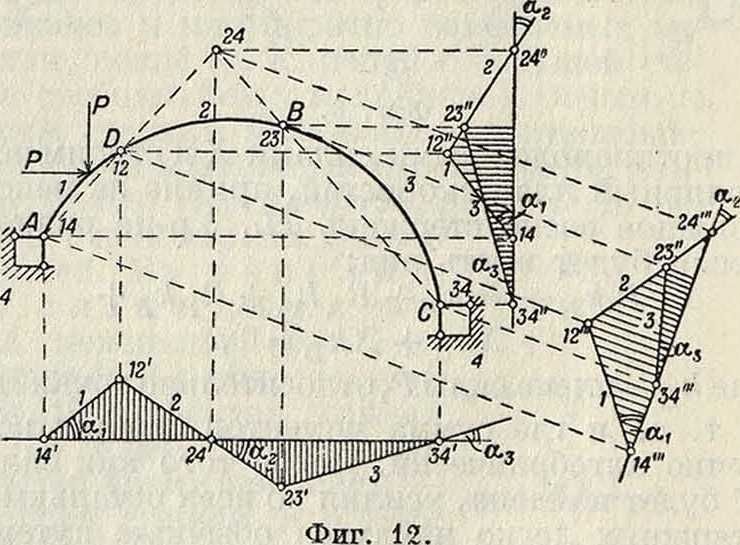
На фигуре 12 показано кинематическое построение инфлюентных линий изгибающего момента в сечении Ώ трехшарнирной арки АВС при трех различных направлениях движущегося груза; равные углы обозна-

пены на всех трех инфлюентных линиях одинаковыми буквами. Для построения всех этих инфлюент достаточно найти мгновенный центр 24, к-рый лежит на пересечении прямых AD и СВ. На фигуре13 показано построение инфлюентных линий для различных стержней балочной фермы при помощи мгновенных центров вращения; все масштабы выписаны на чертеже. На фигуре 14 показано применение неполярного плана скоростей для той же цели. Части а и б фигуры представляют собою инфлю-ентные линии усилия в раскосе D соответственно при езде понизу и поверху; заштрихованное же звено считается неподвижным. Изображение 4 точки 4 помещаем в точке 2 изображения всех остальных узлов строятся без всякого труда; как видно по надписям, целый ряд изображений совпадает между собой. Сближение точек 4 и 2 выражается проекцией вектора 44 на направление, перпендикулярное к Ώ, то есть ν_χ=λ sin φ, где λ—длина панели и φ—угол наклона раскоса D к поясу. Отсюда получаем масштаб: Я sin φ=1.

Вертикальная скорость ν_ρ точек 5, 9, 13 равна 55=99=13 — 13=Я. В точке А получаем ординату 26-26=|=—

В остальных узлах ординаты инфлюенты

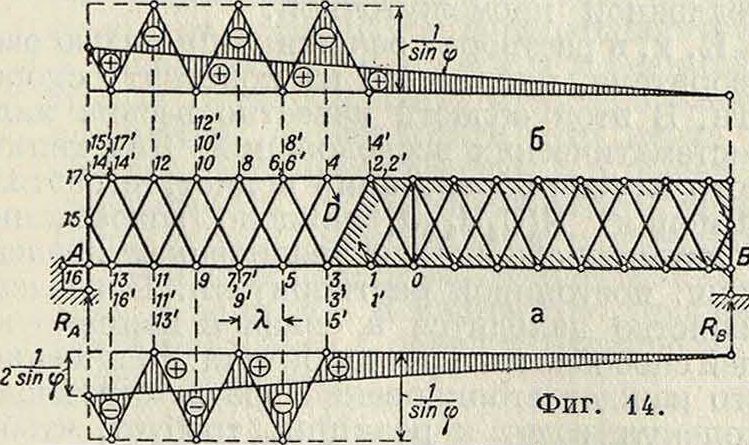
равны нулю. Т. о. получается зигзагообразная инфлюента (фигура 14, а), у которой крайняя правая ордината равна нулю, а крайняя левая=i -¹,·. После этого изменяем не-

2sm ψ

подвижное звено, для чего достаточно провести ось абсцисс так, чтобы крайние ординаты обратились в нуль.

Применение кинематики к решению статически неопределимых задач. Простейшее применение заключается в определении линейных перемещений узлов и узловых перемещений стержней в рамных сооружениях. Для решения этой задачи следует поместить во всех без исключения узлах сооружения шарниры, считать все стержни абсолютно жесткими и для полученной т. о. кинематич. цепи построить план скоростей. Если цепь имеет п степеней свободы, то следует взять п независимых друг от друга возможных перемещений и для каждого из них построить отдельный план скоростей. Из этих планов и определятся графически линейные и узловые перемещения, фигурирующие в статически неопределимой задаче при решении ее по методу деформаций.

Другое более важное применение заключается в чисто графическ. решении статически неопределимых рамных сооружений. По известной теореме Мора, перемещение любой точки стержня по любому направлению м. б. представлено как изгибающий момент от фиктивной нагрузки, выражаемой эпю-м рой -gj, где М—действительный изгибающий момент в любой точке. Эта фиктивная нагрузка должна считаться приложенной к каждому элементу ds по его оси и иметь направление, параллельное интересующему нас перемещению. С изменением направления перемещения необходимо соответственно переменить и направление всех фиктивных сил.

Фиктивная нагрузка действует на ф и к-тивное сооружение: в неподвижной точке данного сооружения фиктивный изгибающий момент равен нулю; в неподвижном (защемленном) сечении фиктивная поперечная сила равна нулю. Фиктивное сооружение, получаемое на этом основании, имеет шарниры в точках, соответствующих неподвижным точкам действительного сооружения, и свободные концы—в защемленных концах действительного сооружения. Построение эпюры моментов сводится к уравновешиванию фиктивной нагрузки на фиктивной кинематич. цепи или на фиктивном дисковом мн-ке.

Лит.: Рабинович И. М., Кинематич. метод в строит, механике в связи с графич. кинематикой и статикой плоских цепей, М., 1928.

Тимошенко С. П., Курс статики сооружений, Л., 1926; Π р о к о ф ь е в И. П„ Теория сооружений, ч. 1, М-, 1926; Мюллер-Бреслау Г., Графич. статика сооружений, т. 1, пер. с немецкого, 2 изд., стр. 391—453, СПБ, 1908. И. Рабинович.