> Техника, страница 52 > Кинетическая теория

Кинетическая теория

Кинетическая теория газов или, в общем смысле, материи выводит дедуктивным путем, на основании немногих предположений о движении и природе молекул (смотрите) вещества, все его физич. и отчасти химическ. свойства. Предполагают (для простоты), что молекулы газа суть материальные точки (с массой тонн), беспорядочно движущиеся в пространстве со скоростями, меняющимися в пределах от 0 до со и обменивающиеся скоростями при столкновении подобно идеально упругим шарам. Такое беспорядочное молекулярное движение называют иногда тепловым движением. Оно позволяет установить закон вероятнейшего распределения скоростей между молекулами данного газа (закон Максвелла), не прибегая ни к каким дальнейшим предположениям о природе сил, действующих при столкновении молекул между собою; при этом также совершенно исключается из рассмотрения возможный переход тепловых движений в интрамолекулярное, и наоборот.

Пусть dN—число молекул в единице объёма, имеющих наперед заданную абсолютную, не зависящую от направления, скорость, лежащую в интервале и и и + du; тогда, согласно максвелловскому распределению, должно иметь место соотношение:

--=4= (^ктУ е~^кпт u² du, (1)

У я где N—все число молекул в заданном объёме, к — нек-рая постоянная. Ф-ия распределения ~ играет в кинетической теории ту же роль, какую играют разнообразные кривые распределения в обыкновенной статистике, то есть умножением любой данной величины, зависящей от абсолютной скорости, на эту ф-ию и интегрированием в пределах изменения скорости молекул определяется среднее значение этой величины. Следующие данные иллюстрируют закон Максвелла для воздуха при 0°.

и, м/ск.	< 100	100—200	200—300	300—400
<4* о, W /о · ·	1	8	17	20
и, м/ск.	400—500	500—600	600—700	> 700
dN 0/ N ’ А · · ·	21	16	9	8

Ф-ия Максвелла достигает максимума (смотрите фигура) при нек-ром значении скорости, называемом наивероятнейшей скоростью (с); для с из (1) легко получается:

Это—та скорость, которой обладает наибольшее число молекул. Функция распределения Максвелла позволяет легко найти выражения для наиважнейших средних величин, с к-рыми оперирует К. т. Для т. н. средней квадратичной скорости д имеет место выражение:

»*->tL=!«²· (3)

Для средней арифметической скорости имеем:

Экспериментальная проверка закона Максвелла была произведена в опытах Ричардсона. Путь, к-рый пробегает молекула от столкновения до столк новения, называют г,г длиною свободного пути. На основании формулы Максвелла для среднего значения этой величины получается следующее выражение (в том случае,

-При Т-27У

---При Т-373 “

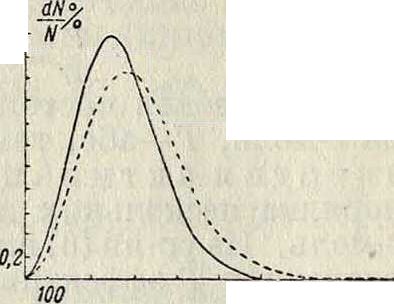
1100 и(м/ск)

когда при столкновении молекул можно-пренебречь силовыми взаимодействиями): А =—i—’ (⁵>

4п<т] 2

где σ—поперечное сечение молекулы, а п— число молекул в 1 см³ газа. Так, для воздуха при 0° и 760 миллиметров Hg Α=7,2·10^-6 см. Как видно из (5), А обратно пропорционально плотности газа: при давлении в 0,01 миллиметров Hg А для воздуха равно уже 0,5 см. Легко показать, что свободный пробег электрона (объём его весьма мал сравнительно с молекулой) Л_е=—, где «и п относятся по-

прежнему к молекуле газа; отсюда А=-4= =

4у2

= 4, что может служить для приближенного определения величины А. Если число частиц, вышедших из данного места, v₀, то число частиц v, прошедших без столкновения путь х, определится из выражения:

—=е.

>’о

Приведенные положения К. т. касаются строго «микроскопических» свойств вещества. Чтобы перейти к характеристике «макроскопических» свойств и тем самым вычислить непосредственно наблюдаемые величины, пришлось выдвинуть новое весьма существенное положение о связи средней кинетической энергии молекулы с Т°; предположили существование наипростейшей связи—линейной:

^mf=”f_=kT. (6)

Соотношением (6) почти целиком исчерпывается логич. схема К. т. Пользуясь законом Максвелла и последним положением, можно строго вывести для идеального газа ур-ие Клапейрона:

pv=~^=NkT=RT. (7)

Здесь р—среднее давление, то есть сила, испытываемая 1 см² стенки сосуда, заключающего газ, вследствие упругих толчков молекул о стенку; /с=~—газовая постоянная,

отнесенная к 1 молекуле и равная 1,37 10^-16 эрг/град. (так называемым константа Больцмана), а R=k-N =8,31·10⁷ эрг/град. моль. К. т. позволяет вычислять средние скорости теплового движения молекул; из (3) и (7) имеем:

д²=—4, где M=Nm—молекулярн. вес газа. Так, для водорода при 0° д=1 840 м/с к, для воздуха д=485 м/ск. Как известно, формула (7) для реальных газов не применима (см.

Газ): она не учитывает ни объёма молекул ни взаимодействия между ними. Ван-дер-Ваальс на основании теоремы Клаузиуса о вириале (смотрите) приспособил ее и к реальным газам. Если макроскопическое—видимое движение газа, как целого, будет различно в различных местах, то благодаря беспорядочному тепловому движению медленные молекулы могут попадать в слои с более быстрым макроскопич. движением и тем самым тормозить движение—переводить энергию видимых (макроскопических) движений в энергию тепловую. Так кинетич. энергия объясняет явления внутреннего трения и для коэфициента внутреннего трения, то есть вязкости η, находит:

Следующая задача, к-рую решала К. т., касалась разбора фактов, связанных с диффузией газов. В зависимости от тех упрощений, к-рыми пользовались различные авторы при рассмотрении этого вопроса, получались несовпадающие результаты. Так, по Мейеру, для коэф-та диффузии газа «самого в себя» получается соотношение:

Ώ=1,34 —,

в где Q—плотность газа. По теории Стефана-Максвелла, то же выражение принимает вид:

D=1,336 ·

’ в

По Ланжевену и Чапману, имеем:

тпп-О Λ

ν=—₃~ =

πιΩ

πσ* 31/2

(8)

Ф-ла(8) показывает, что коэф. вязкости газа не зависит от его плотности, т. к. ни масса молекулы т, ни средняя арифметич. скорость ее, ни сечение молекулы от плотности газа не зависят. Так как средняя арифметическая скорость молекулы пропорциональна средней квадратичной,а этапоследняя на основании соотношения (6) пропорциональна VT, то и коэф-т .вязкости газа должен быть пропорционален VT. Однако этот закон, найденный впервые Максвеллом, оказывается справедливым лишь для немногих газов, более или менее приближающихся к идеальному, и для очень высоких (°.

Для реальных газов, в которых при столкновении молекул играют огромн. роль силовые взаимодействия, Сутерланд уточнил соотношение Максвелла; он дал следующее выражение:

V =

aV т

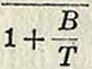
(9)

Здесь А и В — постоянные, зависящие от природы газа. Сравнивая формулы (9) и (8), не трудно видеть, что уточнение Сутерланда коснулось гл. обр. средней величины свободного пробега молекулы, которую нужно считать для реальных газов зависящей от Г. Но и формула Сутерланда не охватывает всего интервала возможного изменения η: при очень низких ί°, как показал опыт, она перестает быть справедливой.

Совершенно аналогично со случаем внутреннего трения К. т. разбирает вопрос о теплопроводности; для коэфициента теплопроводности газа # было получено следующее выражение:

#=* ΜηΩλβ_υ, (10)

где е„—удельная теплоемкость газа при постоянном объёме. Из сравнения формул (10) и (8) легко получить такое соотношение: коэф. теплопроводности газа равняется ко-эф-ту внутреннего трения, умноженному на удельную теплоемкость при постоянном объёме. Более детальный разбор показал однако неточность этого положения. Коэфици-ент теплопроводности только пропорционален указанному произведению, и фактор пропорциональности меняется в небольших пределах от газа к газу.

D=1,200-

’ е

Для коэфициента взаимной диффузии двух разнородных газов получаются у каждого из упомянутых авторов более сложные зависимости.

Несмотря на блестящие результаты, полученные К. т., все же вопрос обоснования максвелловского распределения вызывал большие сомнения. Максвелловское распределение есть отправной пункт почти для всех расчетов в К. т., поэтому всякое, даже небольшое, расхождение с опытом затрагивало максвелловский закон, заставляло вспоминать аксиомы и предположения, лежащие в его основании. На этом пути Максвелл, Больцман и Гиббс создали новую теоретическую, весьма общую дисциплину, так называемым статистич. механику, которая и дала К. т. нужную, вполне оформленную аксиоматику. Максвелл нашел ф-ию распределения для общей механич. системы с конечным числом степеней свободы и показал, что т. н. «закон Максвелла» является предельн. случаем найденной ф-ии распределения, если предположить, что система имеет бесконечн. число степеней свободы, что прибл. имеет место в любой газовой системе. Непосредств. следствием положений, формулированных Максвеллом, является теорема Больцмана о равномерном распределении энергии по степеням свободы.

Толкование с точки зрения К. т. макроскопических свойств вещества и сравнение полученных результатов с опытом дали возможность в то же время составить точное представление и о микроскопических свойствах вещества.

Лит.: Станкевич Б., Кинетич. теория газов, М., 1884; Бачинский А., Введение в кинетич. теорию газов, Москва, 1908; Тимирязев А. К., Кинетич. теория материи, М.—П., 1923; Блох Э., Кинетическая теория газов, пер. с Франц., М.—Л., 1925; Jeans J. Н., The Dynamical Theory of Gases, Cambridge, 1925; Boltzmann L., Vorlesungen uber Gastheorie, T. 1 — 2, 3 Auflage, Leipzig, 1923; Lore n t z H., Kinetische Probleme, Lpz., 1928; H e r z-f e 1 d K., Kinetische Theorie der Warme, Miiller-Pouillets Lehrbuch d. Physik, B. 3 — Warmelehre,

2 Halfte, Brschw., 1925; Clausius It., Die kinetische Theorie d. Gase, die mechanische Warmetheo-rie, B. 3, 2 Aufl., Jena, 1889—1891; Meyer О. E., Kinetische Theorie der Gase, 2 Aufl., Breslau, 1895;

В у k A., Einfuhrung in d. kinetische Theorie d. Gase, Lpz., 1910; Maxwell J. V., On the Dynamical Theorie of Gases, «The Scientific Papers», vol. 2, Cambridge, 1927; To 1 man R., Statistical Mechanics with Applications to Physics a. Chemistry, N. Y., 1927; Ehrenfest P. u. T., Begriffliche Grundlagen d. statistischen Auffassung in d. Mechanik, Enzyklopadie d. mathematischen Wissenschaften, B. 4, T. 2, Abt. 2, H. 6, B.—Lpz., 1914. А. Предводитепев.