> Техника, страница 53 > Клин

Клин

Клин, твердое тело, имеющее две наклоненных друг к другу поверхности; движе

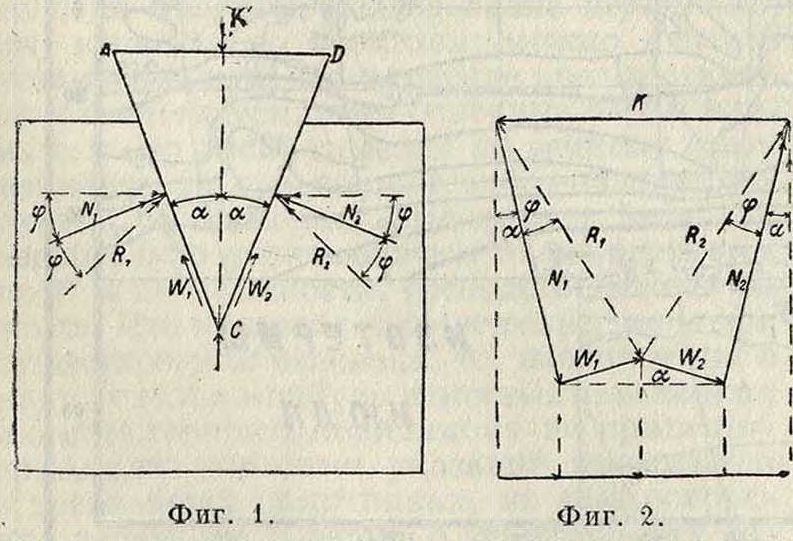
ние клина при его работе совершается по направлению линии, делящей угол клина пополам, в частном случае клин — твердая трехгранная призма с сечением в виде равнобедренного тр-ка ADC (фигура 1). Сторона AD называется обухом К.; на нее действует сила, передаваемая при посредстве К. твердому телу, раскалываемому иод ее действием. В случае равновесия сила, действующая на обух К., при условии отсутствия трения, во столько раз меньше силы давления, испытываемого одной из граней клина, во сколько раз ширина обуха меньше длины рабочей грани клина.

Для рассмотрения действия сил трения N при движении К. построим конусы трения (фигура 1), оси которых идут по линиям действия сил и N₂ сопротивле- *

ния раскалываемого тела, так что R_lt равнодействующая N_± и W_t, или 11₂, равнодействующая N а и W₂, идут по образующим конусов.

Силовой тр-к (фигура 2) дает величину и направление силы К, необходимой для вбивания К. Вместо равнодействующих R₁ и 11₂ для определения силы К могут служить составляющие N_lt W_lt Wг, N₂. Из чертежа легко выводится зависимость:

К=N_X · sin а + W₁ COS а + W₂ COS a -j- N₂ sin a. При Nj=N,=N: W_l=W₂=W=N-tg<p, где φ—угол трения; после упрощений:

Л		hL
Аа	e	r
	l И£>>
	--r~
Фиг- 3.		Фиг

Κ=2Ν sin α + 2N cos a · tg φ =

_ 2 лг sin(a + *p) _

COS<P

Для случая, указанного на фигуре 3 (вытаскивание К.), величина и направление силы К определяются из равенства:

К=N, sin a — W,- cos а — W, cos a 4-+ N₂ sin a.

Если N_t=N₂=N и следовательно Wj== W₂=W=N tgy, to

K=2 N · sin a — 2 N cos a · tg φ =

__ 2 N ^sin(g - g). cgs φ

K=0, если и R₂ совпадают (фигура 4), т. e. если силовой mu-kN₁, W₂, W₂, N₂ замкнутый; аналитически это условие (самоторможения) выразится:

sin (а — <р)=0, или α= ?>, то есть угол при острие К. должен быть менее удвоенного угла трения. В. Никаноров.

К. в машиностроении служит для соединения двух деталей или для установки одной детали относительно другой. Действие К. основано на наклонном расположении его рабочих поверхностей относительно оси клина. Если наклон рабочих поверхностей одинаков, клин называется симметричным, при наклоне только одной поверхности— однобоким. По роду работы различают поперечные и продольные К., к последним относятся шпонки.

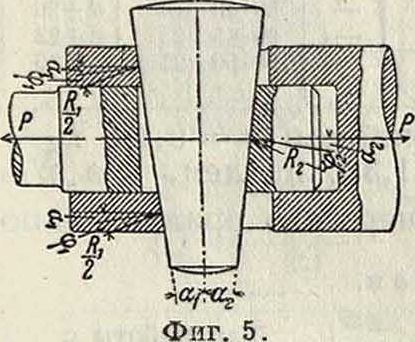
Для общего случая двустороннего К., рабочие поверхности которого наклонены к его оси под углами а_х и а₂ (фигура 5), имеет место следующее соотношение между действующими силами: сила К, действующая вдоль оси К., определяется из ур-ия:

К= R_x sin (ctj + <р_г) + R₂ sin (a₂ + φ₂),

где R_x и Р₂—силы давления, возникающие на рабочих поверхностях К.; <р_х и φ₂ — соответствующие углы трения, причем Rί cos (а₁ + φ_χ)=Р₂ cos (α₂ + φ₂); сила Ρ, действующая вдоль оси штанги, определяется из ур-ия:

Р=COS (α₂ + <р₂).

Из приведенных соотношений следует:

К=Р [tg (α_χ + φ_χ) + tg (a₂ + ςρ₂)].

Для того чтобы удержать К. на месте и не допускать его перемещения под действием сил Р, необходимо вдоль его оси приложить силу

К=Р [tg (ctj - <р_х) + tg (a₂ - φ₂)].

Сила if будет равна нулю в том случае, когда а_х + a₂=φ_χ + <р₂; следовательно для того чтобы К. был самотормозящий, то есть не перемещался от действия сил Р, необходимо следующее условие:

α₁ + α₂^ψι + φ₂;

если К. симметричный (т. e. а_х=а₂) и если Ψ ⁼⁽Ρϊ< то для самоторможения необходимо иметь а_х^<р_х. При однобоком К. а₂=0 и для самоторможения надо иметь: α_χ ίί 2 φ,.

Расчет поперечных клинов (фигура 6) необходимо вести как на смятие его опорных поверхностей, так обязательно и на изгиб. Если клин и его гнездо выполнены достаточно тщательно, так что распределение давления по опорным поверхностям можно принять равномерным, то согласно фигура 6 (на которой для примера изображено клиновое соединение поршневого штока с крейцкопфом) давление р, возникающее на опорных поверхностях К. и штока, определится из уравнения:

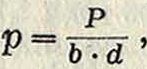
а между К. и горловиной крейцкопфа давление р соответственно определится из ф-лы:, р ^{Р =} b(D-d) ’

следовательно при заданном диаметре d штока ширина К. & и диаметр D горловины определятся из ур-ий:

Для стали давление р при изменяющейся нагрузке принимается ^ 1 500 килограмм/см². Высота К. h определяется по его среднему сечению из расчета на изгиб по ф-ле:

№ ₌ P;D 6 8/1 &

ь=,

+ d.

где W—момент сопротивления сечения К. и 1(_ь—допускаемое напряжение на изгиб. Длина /ц конца штока и h₂ конца горловины берется от >/г до ²/_ad.

Поперечные клины затягиваются со значительным предварительным напряжением. Эти напрялгения во время работы изменяются благодаря действию сил, передаваемых через соединение. Проф. Ретчер дает

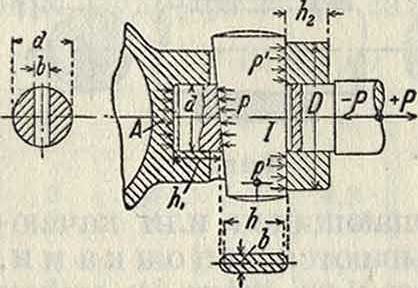
следующий метод определения суммарного напряжения, учитывая влияние упругости материала. Под действием силы Р₀ от предварительной затяжки клина (фигура 7) часть штока под влиянием сжатия будет иметь деформацию <5₀. В то же время тело клина и горловина крейцкопфа, благодаря имеющим место изгибу и растяжению, дадут деформацию А„. Если в некотором мас-Фигура 6. штабе отложить ве личины <5₀ и А₀ перпендикулярно силе Р_в (фигура 8), то при помощи двух полученных треугольников ДВО и ABD можно определить деформации части аb штока (фигура 7), а также К. и горловины крейцкопфа между с я d под действием любой силы, если только пропорциональность между напряжением и деформацией не будет нарушена. Если, например, под влиянием силы Р, действующей по штоку, нагрузка на часть аb увеличится до Р, то деформация части аb увеличится до δ, и в то же время клин и горловина cd разгрузятся на величину, соответствующую разности δ — <5₀. Уменьшая λ₀ на величину δ— δ₀, получим силу Р", под

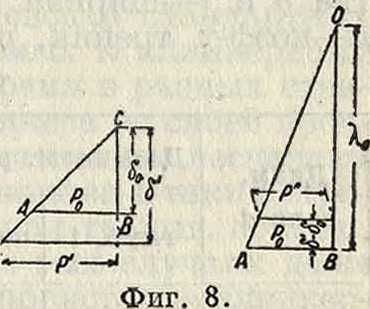
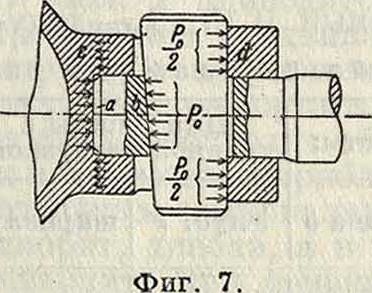
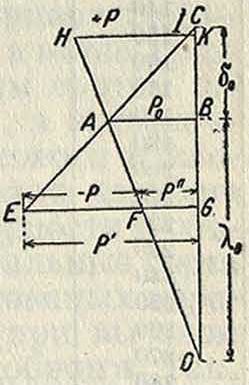
действием которой будет в этом случае находиться К., причем Р — Р" будет равна силе Р. Если тр-ки АВС и ABD сложить их основаниями (фигура 9), то получим простой способ определения деформации под действием внешних сил. Откладывая между AD и продолжением СА параллельно АВ внешнюю силу давления ЕР=—Р, полупим отрезок FG, дающий в масштабе остаточную силу

Р", под действием которой будут находиться клин и горловина крейцкопфа; отрезок EG выражает силу Р, действующую на конец аb штока.

Если к штоку будет приложе- Фигура 9. на растягивающая сила +Р, то, производя аналогичное построение и откладывая отрезок Ш=+Р по другучо сторону от точки А, получим отрезок 1К, выражающий остаточную силу давления, действующую на часть ab штока; отрезок НК соответствует суммарной силе, под действием которой изгибается в этом случае К. и растягивается горловина крейцкопфа. Во время работы соединение соответственно нагружается в пределах от EG до АВ и от АВ до НК.

К., зажатые по всей длине между двумя поверхностями соединяемых деталей, изги-

12

Г. Э. т. X.

бу не подвергаются и поэтому рассчитываются на смятие; К. этого особого весьма распространенного типа с малым уклоном, при помощи которых производят скрепления

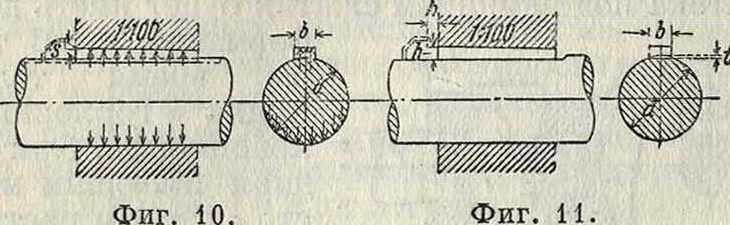
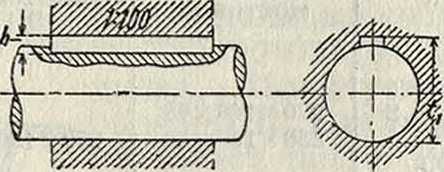
двух совместно вращающихся или качающихся деталей, называются шпонками. Шпонки изготовляются из стали, и уклон шпонки обычно выполняется равным 7₁₀₀. В тех случаях, когда диаметр вала не превышает 150 миллиметров и выполнение шпоночной канавки затруднительно, например при посадке шкива на уже установленном валу, применяются фрикционные шпонки (фигура 10), у которых поверхность, прилегающая к валу, выполняется цилиндрической. При постановке фрикционной шпонки соединение осуществляется исключительно за счет возни-каюхцей при затяжке шпонки силы трения. Необходимое для работы шпонки давление р kbJcm² на ее рабочей поверхности определяется из ур-ия:

-k_d,

где b и Ϊ—ширина и длина шпонки в см, μ—коэф-т трения, равный 0,15; kg—допу скаемое напряжение на кручение вала в килограммах/см²; M_d к гем—крутящий момент, пере-

Т а б л. 1.—Р азмеры шпонок.

Диаметр вала d миллиметров	Фрик цион ная шпон ка	Шпонка, поставленная на лыску		Врезная шпонка
	b s	b h	t	b · h	t
10—12				4-4	2,5	<2 + 1,5
J2—17	—	—	—	5-5	3	d+2
17—22	—	—	—	6-6	3,5	d+2,6
22—Ь’0	8-3	8-4	1	8-7	4	<2+3
30—38	10-3,5	10-5	1,5	30-8	4,5	d+3,5
38—44	12-3,5	12-5	1,5	12-8	4,5	d+3,5
44—50	14-4	14-5	1	34-9	5	d+i
50—58	16-5	16-6	1	16-10	5	d+S
58—68	18-5	38-7	2	18-11	6	d + 5
68-78	20-6	20-8	2	20-12	6	d+6
78—92	24-7	24-9	2	24-14	7	d+7
92—110	28-8	28-10	2	28-16	8	d+S
110—130	32-9	32-11	2	32-18	9	d+9
130—150	36-10	36-13	3	36-20	10	<2+10
150—170	—	40-14	3	40-22	11	<2 + 11
170—200	—	45-16	4	45-25	13	<2 + 32
200—230	—	50-18	4	50-28	14	<2 + 14
230—260	—	—	—	55-30	15	<2 + 15
260—290	—	—	—	60-32	16	<2 + 16
290—330	—	—	—	70-36	18	d + 18
330—380	—	—	—	80-40	20	<2+20
380—440	—	—	—	90-45	23	d+22
440—500			—	100-50	25	d+25

даваемый валом. Принимая μ=0,15, k_d —=200 килограмм/см² и l=l,3d, найдем, что р ss

es200 ^ кг/см². При передаче сравнительно

Таблица 2.—Р азмеры тангенциальных шпонок.

Диам.	Для норм, работы:		Для работы с ударной нагрузкой:				Диам.		Для норм, работы:			Для работы с ударной нагрузкой:
вала <2	глуб. t	ширина Ь	глуб. ί		ширина Ь		вала d		глуб. t		ширина Ь	глуб. t	ширина Ь
60	7	19,3	I				420		30		108,2	42	126
70	7	21,0	—		—		440		30		110,9	44	132
80	8	24,0	—		—		460		30		113.6	46	138
90	8	25,6	—		—		480		34		123,1	48	144
100	9	28.6	10		30		500		34		125.9	50	150
110	9	30,1	11		33		520		34		128,5	52	156
120	10	33,2	12		36		540		38		138,1	54	162
130	10	34.6	13		39		560		3S		140.8	56	168
140	11	37.7	14		42		580		38		143,5	58	174
150	11	39.1	15		45		600		42		153.1	60	180
160	12	42.1	16		48		620		42		155,8	62	186
170	12	43-5	17		51		640		42		158,5	64	192
180	12	44.9	18		54		660		46		168,1	66	198
190	14	49 6	19		57		680		46		170.8	68	204
200	14	51,0	20		60		700		46		173,4	70	210
210	14	52,4	21		63		720		50		183.0	72	216
220	16	57,1	22		66		740		50		185.7	74	222
230	16	58,5	23		69		760		50		188.4	76	228
240	16	59.9	24		72		780		54		198.0	78	234
250	18	64.6	25		75		800		54		200,7	80	240
260	18	66,0	26		78		820		54:		203,4	82	246
270	18	67.4	27		81		840		58		213.0	84	252
280	20	72.1	28		84		860		58		215,7	86	258
290	20	73.5	29		87		880		58		218.4	88	264
300	20	74.8	30		90		900		62		227.9	90	270
320	22	81,0	32		86		920		62		230,6	92	276
340	22	83,6	34		102		940		62		233,2	94	282
360	26	93,2	36		108		960		66		242,9	96	288
380	26	95,9	38		114 !		980		66		245.6	98	294
400	26	98.6	40		120 !		1 ОиО		66		248,3	100	300
Для нормаль- ( &свала *---- ной работы > ра«м^р а-сфиг; 13,· ;				60—150 1 1.-5		160—240 1,5 2		250—340 2 2,5		360—460 2,5 3		480—680 1 4	700—1 000 4 5
Для работ с < Диам. вала				100—220		230—360		380—460		480—580		600—860	880—1 000
ударной нагруз- { Радиус г.				2		3		4		5		6	8
КОЙ	( Размер а.			3		4		5		6		7	9

незначительной мощности и при диам. вала до 230 миллиметров допускается постановка шпонки на лыске, то есть на плоском запиле вала (фигура 11). Необходимо иметь в виду, что изменение направления вращающей вал Силы

Фигура 12.

ведет к ослаблению затяжки такой шпонки, причем не исключается в этом случае возможность разъединения соединенных ей деталей. Врезные шпонки (фигура 12) передают усилие не только возникающей силой трения, но и боковым давлением. Если пренебречь действием силы трейия и защемлением

и считать, что все окружное усилие U воспринимается частью боковой поверхности шпонки с высотою у, то давление р определится из ур-ия:

„ и *d*k_d^у 1-у aiy

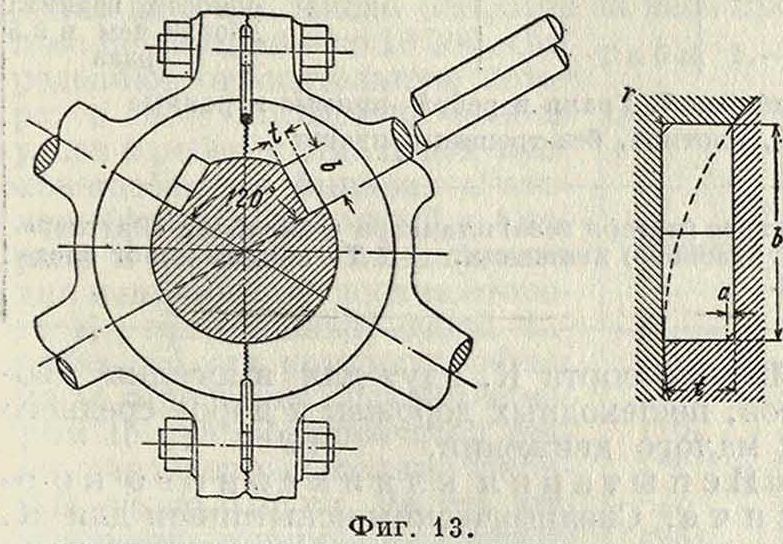
и при длине шпонки I — 1,3d давление Pss 60-. Тангенциальная шпонка (фигура 13)

располагается так, что ее широкая сторона направлена по касательной к окружности сечения вала, а узкая сторона направлена по радиусу вала. У такой шпонки давление воспринимается всей плоскостью стыка, поэтому она может передавать по сравнению с врезной шпонкой значительно Фигура 14. больший момент.

Размеры шпонок в СССР стандартизованы Комитетом по стандартизации (ОСТ 289—299).

В табл. 1 приведены (по DIN 141—143) размеры в миллиметров шпонок фрикционных (фигура 10), поставленных на лыску (фигура 11) и врезных (фигура 12), а также глубина шпоночных дорожек в зависимости от диаметра вала; в таблице 2 — размеры в миллиметров тангенциальных шпонок (по DIN 271 и 288).

Особый вид шпонок представляет шпонка Вудруфа (Woodruff), распространенная в США (фигура 14). Шпонки этого типа изготовляются из протянутой профилированной стали. Гнездо шпонки выфрезовывают дисковым фрезером. Преимуществами шпонок Вуд

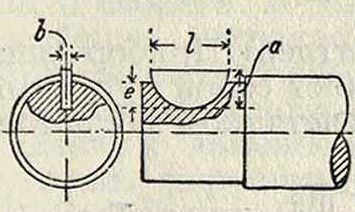
руфа являются: простота выполнения шпоночного гнезда, относительная дешевизна изготовления самой шпонки, точность обработки и удобство ее постановки как с затяжкой, так и без затяжки. Размеры шпонок Вудруфа в миллиметров даны в таблице 3.

Таблица 3.—Р аз меры шпонок Вудруфа.

ь	1	а	е		г	а	е
3	13	5,8	4,3	6	16	6,95	4.95
3	16	6,95	5,45	6	22	9,7	7,7
4	16	6,95	5,45	6	28	12,9	9,9
4	19	8,55	6 ,55	6	32	14,5	11,5
4	22	9,7	7,7	8	19	S,55	6,55
5	16	6,95	4,95	8	32	14,5	11,5
5	19	8,55	6,55	8	38	16,7	13,7
5	25	11,3	8,8

Лит.: Сидоров А. И., Курс деталей машин, 2 изд., ч. 1, М—Л„ 1927; Б оба рык о в ИИ., Детали машин. Часть общая, М.—Л., 1926. Часть специальная, М.— Л., 1927; Rotscher F., Die Maschinenelemente, В. 1, В., 1927. Б. Шпринк.