> Техника, страница 53 > Колебания электрические

Колебания электрические

Колебания электрические, периодически повторяющийся процесс электромагнитных возмущений, очень часто происходящий от естественных причин. Вызываемое искусственно К. э. имеет широкое приложение на практике, в особенности при передаче энергии, в технике связи, в электромедицине, а также в лабораторной технике. К. э. входят как важнейший мотив в современную теорию физич. процессов. Всякая электропроводящая цепь может нести на себе К. э., но не всякая, говоря теоретически, реагирует на них, видоизме няет их, может их возбудить. Для этого электрич. контур должен обладать особыми свойствами; иногда однако достаточно столь слабое их выражение, что практически трудно осуществить контур, совершенно пассивный при К. э., то есть идеально апериодический. Нередко К. э. налагаются на постоянный ток, к-рый получает в таком случае переменную составляющую; всякое изменение постоянного тока—например моменты его замыкания и размыкания — м. б. математически рассматриваемо как наложение целого ряда К. э.

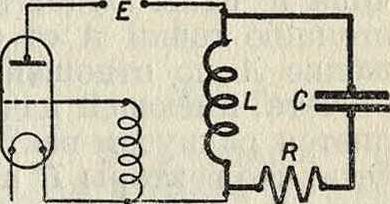
Колебательный контур. В основу всего этого разнообразия явлений, могущих быть подведенными под понятие К. э., полагается идеальный случай свободных колебаний в контуре, обладающем свойствами, делающими его способным к К. э., и предоставленном самому себе (изолированная система). Этими свойствами (случай томсоновских колебаний) обычно принимаются емкость С и самоиндукция L. Поэтому колебательный контур в его основном виде можно представить в виде схемы (фигура 1); на схеме обозначено еще и сопротивление R проводов, соединяющих С иЬ (но существование его не является необходимым для К. э.), а также а и 6—обкладки конденсатора. Т. о. получается колебательный контур—контур относительно малого сопротивления, содержащий самоиндукцию и емкость и обладающий тем свойством, что приложенный к нему тол- ^___

чок напряжения вызывает £³в нем колебательный ток. сг==

Первоначальный толчок, U "НТ

исходный запас энергии, р я м. б. дан такому контуру -WWVWW—

в виде заряда на обклад- фигура i. ках конденсатора или тока по его проводу с соответствующим запасом электромагнитной энергии. Последующие затем К. э. произойдут уже сами собою.

Из предыдущего следует, что колебательный контур должен состоять из элементов, обеспечивающих превращение энергии Электр ич.поля в энергию магнитного поля,и наоборот, т. о., что поступившая в такой контур энергия расходуется не сразу, а претерпевает ряд превращений из одного вида в другой; этими элементами и являются конденсатор С, в диэлектрике которого при прохождении тока смещения меняется запас электрич. энергии, и катушка самоиндукции L, в магнитном поле которой также меняется запас энергии при прохождении переменного тока; кроме того в контуре имеется активное сопротивление, учитывающее не только потери на тепловой эффект Джоуля, но и проч. виды потерь энергии, как то: диэлектрическ. гистерезис, токи Фуко, излучение и т. д. Если в контуре (фигура 1) в данный момент протекает ток г, то эдс самоиндукции равна

(О

а напряжение на конденсаторе равно

e_c~~fidt. (2)

Знак перед правой частью зависит от того, какую обкладку конденсатора мы счита-

ем положительной (выбор положительного направления напряжения на конденсаторе); момент ί₀ выбирается тот, когда напряжение на конденсаторе равно нулю. Тогда

= е_с + iR, (3)

L,f_t+M + ±fidt=0.

t о

Т.о. получаем диференциальное уравнение колебательного контура:

dH. R di, 1 · _ΛdT*+L-di+XC^t=0·	(4)
Решение этого ур-ия имеет вид:
г=1„ е ^а‘ sin (ωί + φ)	(5)
при
©^2<^^илиД<2/с-·	(6)
В контуре получаются колебания,	если за-
ранее был дан некоторый запас	энергии
(1₀Ф0), при этом колебания получаются затухающие (смотрите Затухание). Множитель за-
тухания
II О	(7)
угловая частота
, ¹ л· ^т~У LC 4L-	(8)
и период колебания
ω	(9)

Если условие (6) не выполнено,то получается апериодич. разряд, и контур не м. б. назван колебательным,—его тогда называют апериодическим контуром.

Явление К. э. было открыто теоретически В. Томсоном в 1853 г. Метод его рассуждения заключался в применении закона сохранения энергии к контуру (риг. 1 как изолированной системе; по этому закону, для каждого момента времени полное изменение энергии (электростатической—в конденсаторе, электромагнитной—в среде, окружающей провод, и тепловой— внутри провода) равно нулю. Отсюда Томсон получил ур-ие (колебаний):

<Р« R dq 1 dt* ⁺ L dt CL

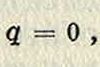
(4а)

где q означает заряд конденсатора в момент t.

Физич. истолкование явления колебаний в контуре таково. Пусть на конденсаторе имеется заряд: на верхней обкладке—положительный и на нижней—отрицательный. Ток пойдет вследствие разряда конденсатора в направлении, противоположном стрелке. Так как в контуре есть самоиндук-ци я, то то к будет рас-t ти постепенно, и также постепенно будет Фигура 2. расходоваться элек трическая энергия,

CV Q*

равная——=₂^, то есть зависящая от величины заряда конденсатора, и будет увели-

Li*

чиваться магнитная энергия —, завися-

щая от силы тока. Это будет продолжаться до тех пор, пока вся электрич. энергия не перейдет в ма.гнитную, то есть пока заряд на конденсаторе не станет равным нулю. Ток далее поддерживается эдс самоиндукции, и направление его то же, что и в предыдущем

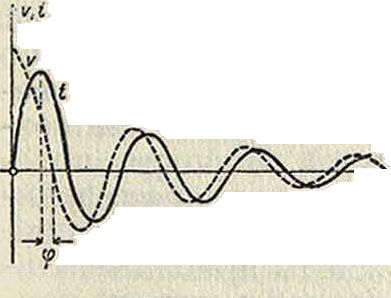
промежутке времени. Вследствие этого конденсатор начинает опять заряжаться, но в противоположном направлении. Магнитная энергия переходит в электрическую, и это происходит до тех пор, пока ток не станет равным нулю, а заряд на конденсаторе не достигнет максимума. Затем последует опять разряд конденсатора и т. д. Фигура 2 показывает изменение напряжения на конденсаторе и силы тока в контуре. Нужно сказать, что сопротивление несколько изменяет эту простую картину. Действительно, если г=1₀ e~^at sin (ωί + φ), το

ν=V₀ e ^αί · sin coi,

где

φ=arc tg “

Угол φ, очевидно, меньше ", следовательно максимум силы тока не совпадает с нулев. значением напряжения на конденсаторе.

Ур-ие (4) имеет простое решение, данное выше, только в том случае, когда постоянные R, L и С не зависят от частоты или от распределения тока вдоль контура. В противном случае вместо одной частоты получается ряд частот. Основная частота, получаемая согласно ур-ию (8),

fo S-hVГс-ПГ>’ (¹⁰>

называемая собственной частотой колебательного контура, однако не совпадает с частотой, соответствующей той эдс, на к-рую контур настроен в резонанс. Эта частота

2πγ LC

и м. б. названа частотой контура при незатухающих колебаниях. Впрочем, в обычных условиях /о и f почти совпадают благодаря незначительному влиянию активного сопротивления.

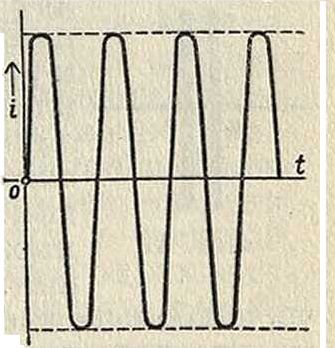
Выражаясь точно, только при R— 0, /о=; в этом единственном случае незатухающих колебаний, при вышеуказанных условиях мы имеем колебания гармонические (фигура 3), то есть каждое из

НИХ СОСТОИТ ИЗ Двух СО- Фигура з. вершенно симметричных половин и T=2n]/LC, эта «томсоновская ф-ла» чрезвычайно часто применяется на практике, и при несоблюденных идеальных условиях, то есть при R>0, считается приблизительно верной. При R=0 происходило бы действительное колебание энергии между двумя ее формами: в течение одного периода электромагнитная энергия ¹l₂LI^!t два раза превращалась бы без потери в электростатическую; ток был бы отстающим на V₄ Т от эдс контура (эдс контура была бы равна эдс самоиндукции),т.е. был быреактивным, и энергия контура не претерпевала бы рассеяния. При затухающих колебаниях, за время Т рассеивается энергия RI*T (по законам синусоидального переменного тока).

и отношение ее к энергии, претерпевающей превращение (то есть приблизительно 2 LI²), rt _s,

равное —j-=о, называется логарифмическим декрементом. Эта очень важная для практики величина, характеризующая поведение контура при явлении резонанса (смотрите), обычно заключается в пределах 0,24-0,02. В тех случаях, когда требуется особенно малый декремент, современная техника уменьшает его еще в тысячу раз (2 10~“). Остальными характерными величинами являются: частота, достигающая на практике 10<Ч-10⁸ ц/ск., а в лаборатории до 10¹³ ц/ск. ,иособый вид сопротивле ния Z =, позволяющий по заданному

I определить наибольшую эдс, появляющуюся у зажимов конденсатора, и обратно: E=j/~~-I.

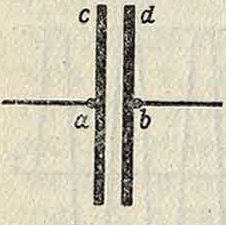
Практические формы и условия К. э. В реальной обстановке явление К. э. весьма осложняется, и уменье подойти к этой сложности в большой мере определяется удачным отделением более существенных факторов от тех, которые в каком-либо данном случае имеют лишь второстепенное значение. Дело в том, что особое практич. значение (для радио) при коротких волнах (смотрите) приобретают К.э.высокой частоты, порядка f=10^е. При таких быстропеременных явлениях выступают уже пространственные соотношения: скорость распространения всякого электромагнитного состояния огромна (порядка скорости света в пустоте), и все же при очень быстрых изменениях сказывается ее конечность; явление не может считаться достигающим одновременно одной и той же фазы в различных точках, хотя бы и отстоящих друг от друга на небольших расстояниях. Так, например точки с и d на периферии обкладок конденсатора (фигура 4) не будут иметь одинаковый потенциал с точками а и 6, через которые заряд поступает к обкладкам; точно так лее различные точки среды, намагничиваемой колебательным током, будут находиться в раз-^фиг. 4. ных фазах магнитного состояния. Все это выступает тем резче,чем больше частота К. э. Поэтому по чисто пространственным причинам, С и L колебательного контура нельзя считать величинами постоянными, не зависящими от со, и ур-ие (4а) получает очень сложный смысл. Есть возможность решать вместо не го, например графически, уравнение со²=~ илиcoL=-L,

предполагающее, как видно из предыдущего, что а=0 (со=со₀), имея из геометрическ. соображений С и L как функции со.

Самое интересное, что дает исследование в этом направлении, это установление существования высших частот, кроме основной, самой низкой, и притом частот не только не кратных, но далее находящихся в ирра-циональн.отношении. Наблюдения подтверждают эту многочастотность колебательного контура, особенно при контурах с очень малым периодом, совсем не обнаруживае

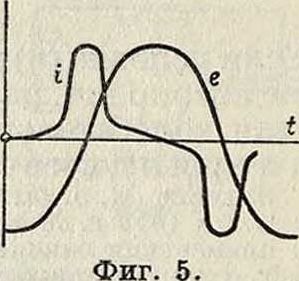
мую при идеальной постановке ур-ия (4а). Вовлечение в рассмотрение величины R еще более усложняет вопрос, т. к. сопротивление тоже является ф-ией частоты проходящего по нему тока (смотрите Скин-эффект). Дальнейшим усложнением является то, что при высоких частотах могут затрагиваться уже молекулярно-дискретные элементы материалов, входящих в колебательный контур и в окружающую его среду, и притом—в резкой зависимости от ω (резонанс молекулы). При таких частотах обычный сердечник в катушке самоиндукции L действует лишь косвенным образом, как предмет, отнимающий энергию от колебательного контура (индукционные печи, диатермическое действие—см. Фуко токи). Но сердечник особо малого сечения намагничивается и обнаруживает периоды резонанса своих молекул (смотрите Магнитная спектроскопия). При меньших частотах, когда сердечник из ферромагнитного материала действует как таковой, выступает зависимость его магнитной проницаемости, а следовательно и L контура, от силы тока в данной намагничивающей катушке, по кривой намагничения данного образца материала. Имея математич. выражение этой кривой, можно получить решение для/контура, к-раяоказывается зависящей от амплитуды колебания, то есть лишенной главного признака гармонии, процесса. Если ввести в рассмотрение еще и гистерезис, то при помощи планиметрирования ход колебательного процесса все же м. б. указан. Фигура 5 изображает изменение эдс е и силы тока г соответственно времени для этого случая.

Как дальнейшие причины искажения синусоидального процесса укажем еще гистерезис диэлектрика и могущую возникнуть в нем проводимость сложного характера, а также сложное участие электронного и ионного процессов в случае существования газового промежутка в колебательном контуре (о чем будет упомянуто ниже). Как известно, всякое искажение синусоиды м. б. рассматриваемо как наложение на основное колебание высших гармонических с соответствующими амплитудами, определяемыми при помощи гармоническ. анализа.

В настоящее время нередко определяют колебательный контур не его периодом, но длиной волны Я, в см, разумея под этим величину Я=3-10¹⁰Т. Такое определение возникло вследствие огромной важности, которую получил в радиотехнике процесс электромагнитного излучения, сопроволедающий К. э. Указанная выше Я, есть приблизительная длина волны, излучаемой в пустоте контуром, обладающим периодом Т. К. э., как показывает ур-ие (4а), выражаются вполне аналогично механически, с заменой меха-нич. свойств системы электрическими и магнитными; при рассмотрении механическ. колебаний системы, колебания предполагаются распространяющимися по ней из той точки, где они возбунщаются, отражающимися от ее границ, могущими образовать стоячие волны, с узлами, отстоящими друг от друга

на V₂ Я. Совершенно так же на электрическом колебательном контуре, способном образовать электрические стоячие волны, установятся узлы тока и пучности, то есть колебательный ток (волна) будет идти по контуру неравноплотным во всех его сечениях. Такой контур будет характеризоваться волнами различной длины, смотря по числу узлов, установившихся по его длине; этим волнам будут соответствовать различные периоды колебаний—обертоны,приблизительно кратные его основному тону. Этот случай Томсон сознательно исключил в самом введении к своему исследованию; иными словами, он рассматривал контур, длина которого весьма мала по сравнению с у» Я и нак-ром умещаются лишь точки около одной пучности; в таком контуре ток через все его сечения ква-зистационарен, то есть практически одинаков с током в самой пучности; кратные обертоны возникнуть не могут. К этому случаю и относится все предыдущее.

Контур, в к-ром образуются стоячие волны, приобрел большое значение как антенна в радиотехнике. Рассмотрение его колебаний усложняется необходимостью приписывать емкость и самоиндукцию каждому элементу контура, т. к. от них зависит скорость распространения волны через этот элемент, определяющая Я и следовательно расстояние между узлами. Задача исследования колебаний при условии таких «распределенных» свойств контура, и притом, вообще говоря, неравномерно распределенных, доходит до математическ. неразрешимости; этой задаче посвящено большое число работ наших авторов (смотрите Радиосети), подходивших к ней как с теоретической, так и экспериментальной стороны. Ур-ие (4а) и фигура 1 относятся к простейшему случаю сосредоточенной емкости (между точками а и Ь).

К. э., сопровождающиеся излучением, в самом своем процессе должны отличаться от того явления, при к-ром участвуют только С, L и R. Излучение, как особое свойство колеблющейся системы, влияет на ход колебательного процесса в каждый его момент. Излучаемое электромагнитное поле, как и поле обыкновенной самоиндукции, воздействует на провод, производящий это поле. Однако в то время как эдс самоиндукции отличается по фазе на ¹/₁Т от протекающего по проводу тока, эдс излучения имеет кроме реактивной еще и активную составляющую. Иными словами, излучение, поскольку оно своей активною составляющей причиняет рассеяние энергии, вносит в колебательный контур свое добавочное сопротивление (называемое сопротивлением излучения) и в то яда время своей реактивною составляющей оно изменяет коэф. самоиндукции контура. Обе эти добавочные величины зависят от со. Аналитическ. выражение этого процесса приводит к диференциальному уравнению 3-го порядка вместо ур-ия (4а).

Техническое использование К. э. Затухающие колебания. При техническ. использовании К. э. весьма важным является вопрос о способе возбуждения их. Оно производится сообщением контуру или первоначальной магнитной энергии соленоида L или электростатич. энергии конденсатора

С. Схема первого способа изображена на фигуре 6. Ток 1₀ от батареи Е, проходящий и через L,намагничивает катушку М; якорь m притягивается, ток прерывается в контакте к, и с этого момента контур LRC предоставляется самому себе; его магнитная энергия переходит в электростатическую заряда конденсатора С, причем развивается эдс

E_max — ~]/~ 1о; при соответствующих величинах LnC она во много десятков раз превосходит первоначальную эдс.Ебатареи.Так начинаются К. э. контура, затухающие затем сообразно его декременту. Та- ”

кая схема возбуждения К. э. нередко имеет место в боль- ф_ИГ. 6.

ших силовых электрических сетях (хотя вовсе не предназначенных для К. э.) и приходит в действие при размыкании тока в соответствующих точках, являясь причиной появления опасных перенапряжений. При обыкновенных контурах высокой частоты колебания, оста-

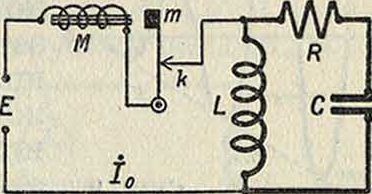
Фигура 6.

ваясь свободными,успевают практически совершенно прекратиться раньше, чем размыкатель Mm упругостью замыкающей цепь пружины снова возбудит их. Схема дает серии (фигура 7) затухающих колебаний, которые разделены сравнительно длинными промежутками времени, в течение которых К. э. отсутствуют. По _f второму способу воз-~ буждения К. э., от источника высокого напряжения заря-Фигура 7. жается конденсатор

С (фигура 8); искровой промежуток аЬ, включенный параллельно С, заряжается при этом до той же Е, и, при соответствующем подборе расстояния ab, в нем проскакивает искра в момент достижения конденсатором той эдс, которую может дать источник. С появлением искры, смыкающей точки а и b своей ионною проводимостью, образуется колебательный контур CRL с запасом электростатич. энергии; в нем произойдут колебания с частотой, определяемой свойствами контура; их затухание будет существенно отличаться от затухания в предыдущем случае, так как проводимость искры будет быстро падать вследствие деионизации (см.

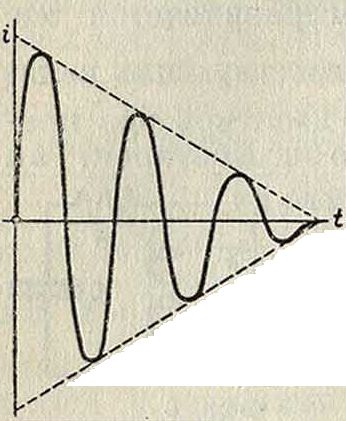
Искровой передатчик) промежутка ab и декремент контура будет возрастать. Теория показывает, что при возбуждении искрой амплитуда колебаний убывает по линейному закону; вместо того чтобы асимптотически приближаться к нулю (фигура 2), амплитуда электрических колебаний обращается в нуль в тот момент, когда эдс конденсатора становится слишком малой для поддержания искрового разряда (фигура 9).

Незатухающие колебания,

а) Общая теория. От схем, служа-

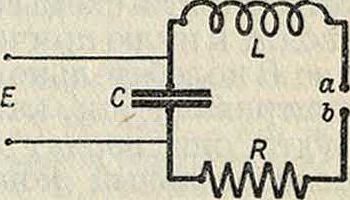
Фигура 8.

щих для возбуждения К. э., следует отличать схемы, имеющие назначение поддерживать на определенной высоте амплитуду уже начавшихся колебаний, то есть превращать их в незатухающие. В этом случае также необходим источникэлектрич. энергии, который должен в течение каждого периода подавать колебательному контуру порцию энергии,как раз восполняющую его рассеяние. Если эта порция будет меньше, колебания останутся затухающими, но с меньшим декрементом, и может случиться, что, при некоторой уменьшенной Фигура 9. амплитуде тока, рассеиваемая за период энергия V₂ RPT станет равной доставляемой от источника порции энергии,—тогда колебания установятся незатухающими. Если, наоборот, эта порция превосходит энергию, рассеиваемую за период, колебания будут возрастающими по амплитуде, пока опять не будет достигнуто стационарн. состояние при достаточно возросшей амплитуде тока. Процесс нарастания колебаний может начинаться с какой угодно малой амплитуды; он может начаться с той чрезвычайно малой амплитуды, которая соответствует случайному, в молекулярно-стати-стич. смысле этого слова, нарушению электромагнитного равновесия систе мы. Так. обр. все это устройство может не иметь ничего общего с возбуждением колебаний. В нашей терминологии еще нет особого слова для этого технич. процесса (по-немецки— Anfa-chung), на к-ром однако уже 15 лет зиждется вся радиотехника. Лучшим источником энергии для такого непрерывного, без перебоев, яодвозбуждения контура какой угодно высокой частоты служат генератор постоянного тока, батарея или выпрямленный сглаженный ток от вторичной обмотки повышающего трансформатора. Т. о. все устройство является преобразователем постоянного тока в переменный (колебательный). Это преобразование достигается весьма различными, часто сложными схемами, связанными с колебательным контуром, в которых действуют механические, эле ктр омагнитные, ионные или электронные процессы. В виду того что эти схемы уничтожают затухание, сводят к нулю причину его, то есть сопротивление R колебательного контура, их часто рассматривают так, как будто они вводят в ^εколебательный контур отрицательное сопротивление (-R)· При таком взгляде становится *—4.

ясным,что рассеяние oj-

энергии при К. э., равное за каждый период ¹/_i(RI²—RI²)T, становится равным нулю при R, численно равном R. Для изучения схемы и расчета ее действия остается лишь уметь выразить R как функцию от ее электромагнитных свойств. Однако многие авторы избегают пользоваться понятием ότ

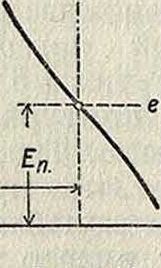
Фигура 10.

рицательного сопротивления, находя логич. противоречие в самом его определении, и производят подсчеты по другому пути.

Схема с источником постоянного тока, служащая для подвозбуждения, дает силу тока I и эдс Е вида

5? I — In. + Й Щ⁼ Еп. + ^е f где 1_п. и Е_п_—постоянные слагающие, а г и е—чисто переменные, то есть такие, что за время полного периода Ji dt=0 и Je dt — 0. Мощность такой схемы получает вырал-сение ψJdt=Е_П-1_П + fjiei dt, (11)

где интегралы берутся за время Т. Т. к.пере-менные слагающие должны давать подвозбуждение, а не рассеяние, как Е_п_ и 1_Пш> то необходимо, чтобы второе слагаемое имело знак, обратный знаку первого, которое мы считаем > 0. Следовательно е и г должен быть всегда

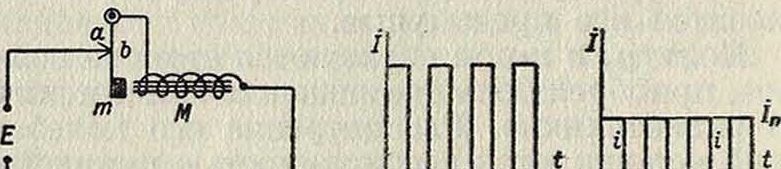
I- ΛΛΛΛΛΛ/—

Фигура 11.

Фигура 12.

противоположных знаков. Иными словами, если возьмем Е и I за оси координат и перенесем начало их в точку (Е_п-> 1_п_),то, изображая кривою (т. н. характеристикой схемы) ход переменных е и г, должны получить ее лежащей во втором и четвертом квадрантах (фигура 10). Такая «падающая» характеристика схемы (при увеличении переменной слагающей тока г переменная слагающая напряжения е падает, и наоборот) является столь же необходимым и достаточным условием получения незатухающих колебаний, как и отрицательное сопротивление. Оба эти представления говорят о двух сторонах одного и того же свойства схемы подвозбуждения. Кпд такой схемы выражается отношением

j; f ^ei_^dt

Еп. In· ⁹

по уравнению (11) оно равно 1 (100%), если dt=0, то есть если maximum Е соответствует 2=0 и наоборот. Такое соотношение имеет место в простейшей (и притом еще идеализованной) схеме незатухающих колебаний (фигура 11). Между точками а и b напряжение максимально при разомкнутом прерывателе, и если оно равно нулю при замкнутом (ток максимальный), то”мы имеем идеальный случай (кпд=100%, фигура 12). Легко показать, что при таком устройстве, которое дает синусоидальный ток, наибольший кпд=50%.

б) К. э. при дуговом генераторе. Вольтова дуга имеет падающую характеристику; основная схема для использования ее как средства подвозбуждения изображена на фигуре 13. Здесь мы видим, что вольтова дуга В с ее отрицательным сопротивлением включена в колебательный контур последовательно с сопротивлением R,

что и служит к непосредственному сведению его к нулю. Сложный электронно-ионный процесс, происходящий в вольтовой дуге, сильно искажает форму колебаний, поддерживаемых ей в контуре. В зависимости от ргщоч-гпЛАЛг-е в| cs

яз

t 1

Ιί

е-Т,—

с Т

]/1

Фигура 15.

Фигура 13.

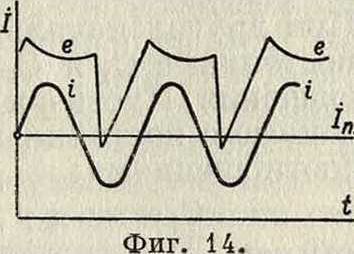
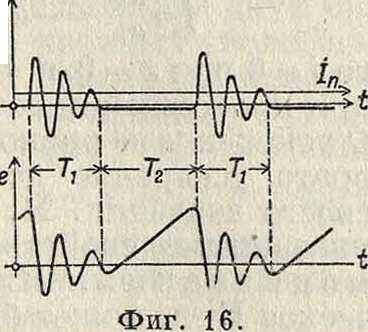
условий, в которые поставлена вольтова дуга,—например от возможности быстрого охлаждения ее электродов (их температура определяет электронную сторону процесса) и быстрой деионизации воздушного промежутка,—колебания получаются трех родов {Симон, Баркгаузен). Колебания 1-го рода {фигура 14) представляют собою синусоидальн. ток, налагающийся на постоянный 1_п- при сильно искаженных колебаниях напряжения на конденсаторе. Колебания 2-го рода (фигура 15), являющиеся наиболее важными для техники, происходят при малом 1,_и, за время Т₂ ток отсутствует; Ί м. б. получено в пределах между π j LC и 2 л ]/LG· Колебания 3-го рода (фигура 16) подобны тем сериям затухающих колебаний, которые возбуждаются искрой (фигура 9); кривая изменения напряжения на конденсаторе показывает нарастание его во время отсутствия тока в контуре до той величины, при которой зажигается вольтова дуга; благодаря последней снова начинаются колебания. Фигура 14 — 16 показывают своим сложным видом, в какой малой степени явления, производимые «дуговым генератором», отвечают потребности практики в чистых синусоидальных колебаниях с постоянной амплитудой. И тем не менее техника достигала удовлетворительного разрешения своих задач, хотя при этом и требовалось большое искусство управления дуговою схемой. в) К. э. при помощи электронной лампы. За последние 10 лет вошел во всеобщее употреб- _έ· ление новый метод получения незатухающих колебаний—при помощи электронной лампы. Лампа включается параллельно колебательному контуру (см.выше фигура 17); здесь пользуются отрицательным сопротивлением в ответвлении. Разрядный процесс в электронной лампе, особенно если она эвакуирована до технического предела, значительно проще, чем в вольтовой дуге; поэтому аналитическое выражение действия ламповой схемы путем ряда приближений (Валлаури, Баркгаузен, Бонч-Бруевич, Шоттки,” Ван-дер-Поль) получает все

Фигура 17.

большую точность. Ламповая схема получила дальнейшее усовершенствование, и в то же время усложнение, в виде стабилизатора. Дело в том, что режим, с которым работает лампа, легко может несколько измениться, что ведет к изменению даваемого схемой периода—изменению небольшому, но уже недопустимому при современных методах радиопередачи. Во избежание этого явления в схему вводится вещество (пьезоэлектрическое или магнитострикционное), в к-ром под действием электрич. колебаний возбуждаются механич. колебания, оказывающиеся необычайно устойчивыми; влияя обратно на электрические процессы, они стабилизуют элек-трическ. колебания.

Рассмотрение таких схем приводит к ди-ференциальным уравнениям высших порядков, с которыми давно уже приходилось иметь дело в теории колебаний связанных систем (М. Вин, Мауц, Татаринов), обогатившейся за последнее время понятием о затягивании (смотрите Ламповые генераторы).

Следует упомянуть в заключение о совсем новом понятии параметрических колебаний, практич. применение которых еще только предвидится, и о так называется нетом-соновских колебаниях. При этих последних самоиндукция контура играет второстепенную роль и м. б. очень малой; они происходят, если R>2y, что делает невозможными колебания томсоновские; их период определяется величинами С и R. Из многочисленных схем, применяемых радистами и физиологами для получения нетомсо-новских колебаний, упомянем ту, которая основана на свойстве неоновой (тлеющей) лампы пропускать ток лишь при достижении известного напряжения Е₀ на ее электродах. Источник постоянного напряжения Е> Е₀через сопротивление R заряжает емкость С (фигура 18); по достижении емкостью напряжения Е₀ неоновая лампа N разряжает конденсатор, который затем снова заряжается. Промежуток времени между двумя зарядами регулируется величинами С и R.

Лит.: Электрические колебания и волны, сб. под ред. В. Лебединского, вып.2, СПБ, 1911; Петровский А., Радиосети (литогр.), Л., 1924; его ж е. Научные основания беспроволочной телеграфии, ч. 1, СПБ, 1913; Иваповский В., Теоретич. исследование колебаний в связанных системах, П., 1917; Фреймам И., Курс радиотехники, 2 изд., М,—Л., 1928; Луценко Η. Н., Основы теории радиотехники, Л., 1927; «ТиТбП» с 1918; Nes per E., Handb. d. drahtl. Telegraphie u. Telephonie, B., 1921; О llendorffF., Grand lagen d. Hochfreciuenztech-nik, Berlin, 1926; Zenneck .T. u. Rukop H., Lelirbuch d. drahtl. Telegraphie, 5 Auflage, Stg., 1925; Pierce G., Electromagnetic Oscillations a. Electric Waves, N. Y., 1920. В. Лебединский.

Колебания электрические

j; f ei_dt

j; f ^ei_^dt