> Техника, страница 53 > Колебательное движение

Колебательное движение

Колебательное движение, движение, при котором материальная точка (или тело) периодически проходит под воздействием приложенных сил через одно и то же положение устойчивого равновесия. В

Фигура 1

зависимости от характера приложенных сил К. д. бывают различны. Основными видами К. д. являются следующие.

К. д. материальной точки, находящейся под действием силы притяжения, пропорциональной расстоянию. Пусть нек-рая материаль-

__{и а}__я ная точка А массы

Г л_—д. * т (фигура 1) находит-

«-¹-j ^ ^г_ —jj-x ся под действием

^F силы-Р, притягива-

фигура 1. ющей ее к некото рому центру притяжения О, причем пусть абсолютная величина F силы будет пропорциональна расстоянию точки 4 от О. Пусть, далее, положение А по отношению к некоторой системе отсчета, имеющей начало в точке О, определяется радиусом-вектором г. Нетрудно видеть, что векторы F я г, находясь на одной прямой, х, направлены в противоположные стороны, и т. к. кроме,того Fur прямо пропорциональны, то

Р-Ы*Г, (1)

где λ²—существенно положительный фактор пропорциональности между величинами Fur. Так как по основной формуле динамики (смотрите Механика теоретическая)

™%=F, (2)

то получается следующее ур-ие, определяющее движение точки А:

(3)

или, обозначая для простоты абсолютную ве-

у“

личину вектора г через х, а — через 7с²,

лиг + к²х — 0. (4)

Проинтегрировав последнее диференциаль-ное ур-ие, найдем функциональную зависимость переменной величины ж от времени t, а взяв далее производную х по ί, найдем и функциональную зависимость скорости ν от времени ί, т. к. точка А движется прямолинейно по оси х. Обе найденные т. о. функциональные зависимости вполне определяют характер движения материальной точки. Общий интеграл дифер. ур-ия (4) имеет следующий вид (смотрите Диференциалъные уравнения):

х=Се^ш + С"е~^ш, (5)

где е—основание натуральных логарифмов. Пользуясь ф-лами Эйлера:

е^±ш=cos kt + г sin kt, (6)

можно общему интегралу (5) придать еще и следующий вид:

х ·= C₁ sin kt + С₂ cos Tei, (7)

где С! и С₂—нек-рые постоянные, определяющиеся из начальных условий движения. Взяв производную ж по ί, получаем из (7):

ν=ν_χ=^=С_гк cos Ы — С_гк sin Ы. (8)

Если в начальный момент точка А находилась в О, имея скорость «₀,то есть если ж=0 и ν=υ₀ при ί =0, то постоянные интеграции С_ги С₂ принимают след, частные значения:

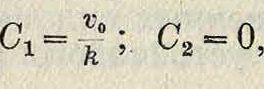
так что равенства (7) и (8) принимают Следующий частный вид:

х=~ sin kt, (9)

ν=г>₀ cos kt. (10)

При других начальных условиях движения постоянные C₁ и С₂ имеют конечно другие значения. Пусть а и γ—две постоянные, связанные с постоянными C₁ и С₂ следующими соотношениями:

C₁=e cos γ, С₂=а sin γ, (11)

так что

α= VCI + CI и tgγ= · (11)

Вставляя значения (11) в (7), получаем третий вид общего интеграла дифер. ур-ия (4), а именно:

х=a sin (kt + γ). (12)

Из рассмотрения равенства (12) можно непосредственно сделать следующие выводы. 1) Так как правая часть (12) периодическая ф-ия от ί, то и величина х периодическая ф-ия от t, то есть точка А будет периодически находиться на одном и том же расстоянии от центра О, другими словами, точка А будет совершать К. д. около О. 2) Абсолютная максимальная величина ж равна «=СШ== у С! + С1; это максимальное расстояние 4 от О называется амплитудой колебания. 3) Если время ί увеличивается на про-

межуток времени Т =, то и расстояние х принимает прежнее свое значение. В самом деле, если в момент ij=t + ~ точка А находится от О на расстоянии ж_1; то

= a sin (ktx + γ)=a sin (ί + ^ + y]== a sin (kt +γ)=χ.

Промежуток времени T=~, по истечении которого точка вновь находится в прежнем своем положении, называется полным периодом колебания. 4) Так как

ν=~=ак cos (kt + γ), (13)

то величина ν достигает максимума, когда ж=0, то есть точка А будет иметь наибольшую скорость при прохождении через центр О.

5) Т. к. ускорение j равно в данном случае

-ак² sin (kt + γ), (14)

то j=0 при 1=0 и ί=j_max при ν·= 0, то есть при прохождении точки А через положение О ускорение ее равно нулю, а в точках возврата ускорение достигает максимального своего значения. К. д., обладающее вышеуказанными свойствами, называется гармоническим. Кинематически гармоническое К. д. может быть представлено след, обр. Пусть нек-рая точка движется равномерно с постоянною угловою скоростью к по окружности радиуса а, имеющей центр в точке О. Пусть начало отсчета угловых перемещений будет ОМ (фигура 2) и пусть при 7=0 точка находилась в положении _Р₀, определяемом углом Р₀ОМ=γ. По истечении времени ί угловое перемещение точки равно kt, а угловое расстояние от начала отсчета углов

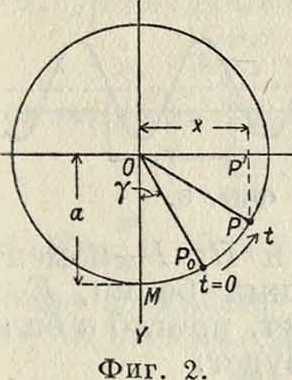
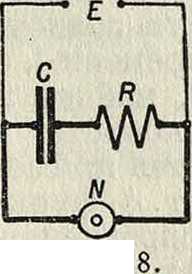
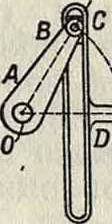
равно kt+γ. Проектируя точку в ее положении Р на прямую ОХ, перпендикулярную ОМ, получим проекцию P, отстоящую от О на расстоянии OP =х=а sin (kt+γ). Т. о. видно, что проекция на диаметр окружности точки, совершающей равномерное круговое движение, совершает гармоническое К. д. Механич. -х схема, соответствующая вышеуказанному кинема-тич. представлению гармонического К. д., приведена на фигуре 3, где: АВ—кривошип, О—неподвижная ось кривошипа, С—ползун, ΌΕ—шток поршня, KL—поршень. Нетрудно усмотреть на основании сказанного, что если кривошип будет равномерно вращаться около оси О, то поршень будет совершать гармоническое К. д. Исходя из этих кинематич. соображений, величину kt + γ правой части (12) называют фазовым углом, или фазой, К. д. в момент t, а γ—н ачальной фазой.

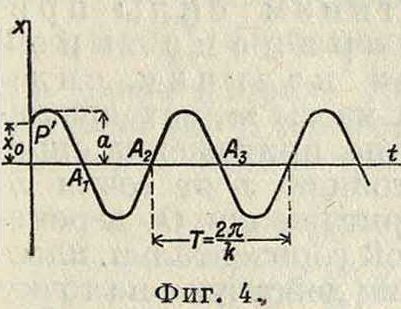
Если по оси абсцисс ортогональной системы осей координат откладывать значения t, а по оси ординат—соответствующие значения х из (12), то в результате получается синусоидальная кривая, представляющая графически изменение х в зависимости от t (фигура 4).

В общем случае кривая пересекает ось ординат в Р, так что ОР —х₀=а sin γ,т. к. это соответствует моменту 1=0. Кривая пересекает ось абсцисс последовательно в точках А_г, Л₂, А₃, ., отстоящих дпуг от друга т на расстоянии, равном —. Два К. д., имеющих один и тот же период колебания, называются синхронными. Если имеются два несинхронных К. д.

Фигура 3.

х — a sin (Ы + у) и х — сь sin (kt -f- γ), так что кФк, то разность фазовых углов (kt + γ) — (kt + γ) называется сдвигом фаз в момент t. Так как при синхронных колебаниях к= к, то сдвиг фаз двух синхронных колебаний равен в любой момент начальному сдвигу фаз γ — γ. Величина

1 ft

V=ψ «= показывающая, сколько полных колебаний совершает точка в единицу времени, называется частотой колебания.

К типу дифер. ур-ия (4) приводятся во многих случаях дифер.ур-ия движения, как например ур-ие движения математич. маятника, то есть материальной точки, вынужденной перемещаться по дуге окружности. Связью, вынуждающей точку совершать движение по окружности, может служить либо нерастяжимая нить длиною I, закрепленная в некоторой точке О, либо шаровая поверхность

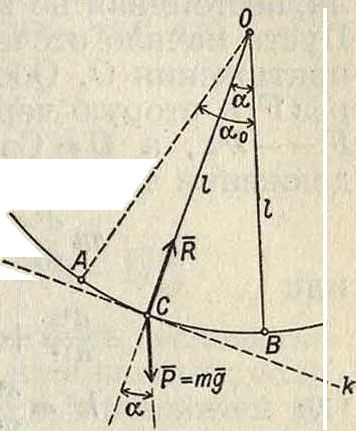
радиуса I с центром в точке О (фигура 5). Параметром, определяющим положение точки в положении С, пусть будет угол ВОС=а, где ВО—вертикальная прямая, проходящая через точку О. Пусть в момент 1=0 точка находилась в положении А, определяемом углом а₀, имея скорость ν=0.

В положении С на точку, при отсутствии сил трения, действуют сила веса Р= mg и сила реакции связи В, так что mj=P + R, (15) или Р + R — mj=0, где j—вектор полного у CKO- Фигура S.

рения точки в рассматриваемом положении. Т. к. проекция j на направление касательной к равна по абсолютному значению

I. i dv _ d(l(o) deo__, d²a

¹ 7* * ~dt~ ~dt~ ~¹ dt~ ¹ dt* ’

а при движении сверху вниз

. _Ί d*a

^{= —} ^ di* ’

то, проектируя (15) на это же направление, получаем:

• (16)

ml ^d,° + mg sin a=0,

или

dt _Ί d²a,

l^ + gsma.

0.

(17)

При малых колебаниях можно, вследствие малости угла а заменить sin a через a. Тогда вместо (17) имеем приближенную формулу:

d²a д _Λdt» +!^a=0’

(18)

аналогичную дифер. ур-ию (4), где вместо коэф-та /с² имеем ®. Общий интеграл имеет поэтому вид, аналогичный (7):

a=С_г sin j t) + C₂ cos (j/^f i), (19) а угловая скорость ω равняется

^{(0 =} Ш^=С^У^Г г^С08(/"?*)-

-C₂|/^sin(|/® i). (20)

При данных начальных условиях движения С_х=0, С₂=а₀ так что вместо (19) и (20)

имеем:

α= о_а COS

Полный период колебания будет равен:

Мг=^Г^2π/;· (2d

Точное интегрирование дифер. ур-ия (17) приводит к эллиптическим функциям.

К. д. под действием силы притяжения, пропорциональной расстоянию, и силы, постоянной по величине и направлению. Допустим, что на точку массы m действуют две силы, линии действия которых совпада-

ют с направлением оси ж: одна из них есть сила притяжения к некоторому центру О, прямо пропорциональная расстоянию от материальной точки до точки О, а другая—сила, постоянная по величине и направлению. Пусть начало отсчета оси ж взято в центре притяжения О. Обозначая первую силу через F, а вторую через Q, имеем попрежнему Ρ=— λ²χ, a Q=Const, так что дифер. ур-ие движения точки будет:

где

m~=-X²x + Q,

Μ=^λ- и S=-§ ·

(22)

(23)

Нетрудно видеть, что дифер. ур-ие (23) м. б. приведено к типу (4) и что следовательно и в рассматриваемом случае точка будет совершать гармоническое К. д. В самом деле из (23) имеем:

d^lx di*

-S-кb; ^=-/е²(ж-|,), S_

ft*

f?!?__Ь2,

dl* ^KZ’

(24)

т. e. получаем дифер. ур-ие типа (4). Так как центр колебания, определяемого (24), находится в точке г= 0, то расстояние ж₀ от центра колебания С до начала отсчета О, совпадающего с центром притяжения, определяется из равенства:

х_с-

Т. о. видно, что центр притяжения О уже не совпадает с центром колебания С, как это имело место в рассмотренном выше случае. Точка С отстоит от О на расстоянии d=~ в сторону действия постоянной силы Q. Так о как далее есть частный интеграл дифер. ур-ия (23), то, принимая во внимание, что (7) есть общий интеграл дифер. ур-ия (4), получим общий интеграл дифер. уравнения (23) в следующем виде:

х=С₁ sin kt + С₂ cos kt + · (25)

Отсюда имеем:

v= Cifccosfci — С₂к sin kt. (26) Если в начальный момент точка находилась в О, имея при этом нулевую скорость, то есть если ж=0 и v=0, при ί=0, то С_х=0 и

С₂— —, так что вместо (25) и (26) имеем:

S

"ft*

s

cos kt + jj ;

v=v sin kt.

к

(250 (260

В частности, силою Q может служить вес тела Р=тд, а силою F—сила натяжения вертикальной пружины. Тогда вместо ур-ий (23), (250 и (260 получаем соответственно уравнения:

d²x. ₇ о

_w + k-x-g,

Х=~{г COSfci+|;> v=-- sin kt.

к м.

Откладывая значения х по оси ординат, а значения t по оси абсцисс, получаем кривую, изображенную на фигуре 6.

Примером для рассмотренного вида К. д. может служить горизонтальная балка, опирающаяся на две опоры в двух точках 4иВи нагруженная посредине грузом Р, причем весом самой балки пренебрегаем. Если I—длина балки между А и В, I—момент инерции поперечного сечения балки, Е— модуль упругости, то статич. прогиб а балки под действием силы Р будет: _a==_i!_p

б“ 4 0 ГГ Г ?

Фиг.

—Т-6.

или, если обозначить

48ΕΙ ‘

Α8ΕΙ <jn

-γ₃— через Я²,

или Р=αλ².

Под действием силы Р балка в положении равновесия будет иметь изогнутый вид. Для того чтобы прогиб балки стад ж, нужно, чтобы на середину балки действовала сила

P, но при этом отношение ~ должно рав-

р няться отношению —, то есть Р=А²ж. Если балку вывести из состояния покоя, то она начнет колебаться, причем в положении, определяемом прогибом ж, на середину балки будут действовать две силы: сила веса груза Р=тд и сила упругой деформации самой балки, стремящаяся привести ее в горизонт, положение и пропорциональная величине ж, то есть сила Р_г=— λ²χ. Ур-ие движения середины балки принимает в таком случае вид, аналогичный ур-шо (22), а именно:

m ™=— А²ж + тд, или ~ + к²х=д.

Середина балки будет т. о. совершать гармоническое К. д. около нек-рого центра колебания, отстоящего книзу от прямой АВ на расстоянии д _ дт _ Р 1³

ft* Л* 48 EI

Все прочие общие выводы применимы и к этому частному случаю.

К."д. под действием силы притяжения, пропорциональной расстоянию, при наличии силы трения. Если точка массы т, находящаяся под действием силы притяжения, пропорциональной расстоянию ж от точки до некоторого центра притяжения О, перемещается по шероховатой горизонтальн. плоскости, то при движении действуют на точку следующ. силы: сила притяжения F=—λ²χ, сила веса Р=тд, сила трения T=fmg (где f—коэф. трения движения) и сила реакции плоскости В. Т. к. сила Т, оставаясь постоянной по величине, меняет свое направление в зависимости от направления движения точки (этим сила Т отличается от силы Q предыдущего случая, сохраняющей постоянными как величину, так и направление), то ур-ие движения точки будет менять свой вид в зависимости от того, движется ли точка справа налево или наоборот. В первом случае, то есть при г><0, сила Т направлена в положи-

тельную сторону оси (фигура 7), так что дифер. ур-ие принимает вид:

(27)

m ~=- Х^гх + fmg ;

при движении же слева направо, то есть при ι;>0, ур-ие движения будет:

^d‘^x;=— λ²χ — fmg. (27)

m

dt*

(28)

Рассматривая 1-й случай, имеем из (27):

~ + wx=fg,

где к²=^. Так как полученное ур-ие (28)

вполне совпадает по виду с дифер. ур-ием (23), то отсюда следует, что, при рассмат-J)? риваемом движении

— ^ _т точки справо налево,

ΜβΛψ——х точка совершает гар-1P ионическое К. д.око-

i

1р ло некоторогодентра колебания О_и отстоящего от центра при-* тяжения О на рас-

ία

СТОЯНИИ Хо_х=ВСТО-

Фигура 7.

рону действующ, силы трения Т, играющей т. о. роль силы Q. Общий интеграл дифер. ур-ия (28) будет, аналогично (25),

х=C₁. sin kt + С₂ cos kt + ~· (29)

Если х=Χι и υ — 0, при ί=0, то есть если время начать отсчитывать с того момента, когда точка, отведенная в сторону на расстояние asj предоставлена сама себе, то ур-ие движения (29) принимает следующий частный вид:

X=(я!— Щ COS kt+ ~ (30)

Отсюда имеем также выражение для скорости:

V=-{х_г— Щ к sin kt. (30)

Скорость υ вновь превратится в 0, при условии, что sin kt=0, то есть при kt=лили ί=·£·.· В этот момент х будет иметь след, значение:

Т. о. по абсолютному своему значению второй полуразмах х₂ меньше первого полуразмаха х_х на 2 ~. При последующем движении точки слева направо уравнение движения будет вида (27), а вместо ур-ий (30) и (30) будем иметь соответственно:

*-(-**+£i)cosfct-~ ;

»= (ж₂ - Щ к sin kt.

Так как скорость υ вновь превратится в 0 спустя опять промежуток времени, то третий полуразмах х₃ будет:

^жз= - (-“. + Э - %=- 20, “ т. Д-

Из рассмотрения дифер. ур-ия (27) видно, что в своем обратном движении точка опять будет совершать гармоническое К. д., но уже около центра колебания 0₂, отстоящего слева от О на расстоянии —. В своем дальней

шем движении справа налево точка опять совершает гармоническое К. д. около центра 0₃, совпадающего с прежним центром О_г, и т. д. Полуразмахи же х_1г х₂, х_а,. по своей абсолютной величине образуют убывающую арифметическую прогрессию, так что х₂=Χι -

х - 2 ^ *2 *

о 1я ^ύ к‘ ’

= *ι-4^

^хп — ^χη-ι — Z № ^{= χ}1 ~ 2 (η — ΐ)~

Полуразмахи не стремятся стать бесконечно малыми. Движение точки прекратится, если какой-нибудь полуразмах х_г становится по абсолютному своему значению меньше 2,

т. к. в этом случае не может иметь места равенство х_г+х=х_г—2¹? (ж_{г + 1} и ~ суть по

X	с
U		Н-Д	t
н	"V Гм“"	W1	~L
	I	О
	8

фигура 8.

ложительные величины). Как видно из предыдущего, промежуток времени между поло-

2 л жениями точки х_х и x_z равен -γ; таков же и промежуток времени между положениями точки ж₃ и х_ь и т. д. Т. о. период полного колебания будет и в рассматриваемом случае равен Т — ~, несмотря на убывание величины размахов. Такое движение называется изохронным. Откладывая значение х по оси ординат, а значения t по оси абсцисс, получаемкри-вую, представлен- (3 ную на фигуре 8 и со- "bAj. стоящую из отдель-

ных частей синусоид АО_хВ, В0₃С,

C0₃D,., причем для этих частей центрами симметрии служат О_х, 0₂, 0₃, 0₄₎. располагающиеся попеременно на прямых K_XL_X и K₃L₃, отстоящих с обеих сторон от оси t каждая на расстоянии ~.

В качестве примера рассматриваемого вида движения могут служить движения грузов в регуляторе Гар-тунга (фигура 9) во время вращательного движения последнего около N своей оси. Пусть конец пружины, прижимающий грузН к грузу А, в спокойном состоянии отстоит от оси вращения KL на расстоянии х₀. Если привести стержень MN в равномерное вращательное движение около вертикальной оси KL, то груз А сожмет пружину. В положении, когда конец пружины отстоит от оси KL на расстоянии х, на груз А действуют следующие силы: центробежная сила m —=тхш^г (где ω—угловая скорость вращения), сила трения о стержень,

18

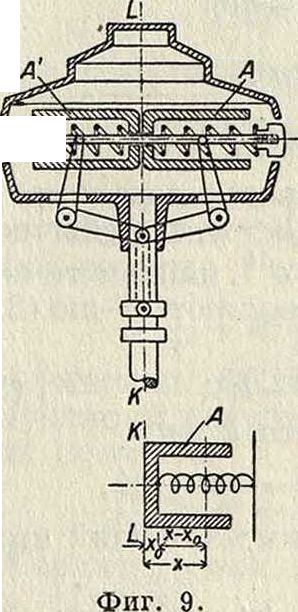
Т. 9. m. X.

равная mgf (где f—коэф. трения), и сила напряжения пружины Я^а (аз — ш₀), где λ²—фактор пропорциональности между напряжением пружины и ее сжатием х — х₀. Т. к. все эти силы действуют по направлению оси стержня ΜΝ, к-рую берем за ось X, то уравнение движения груза принимает следующий вид:

т ~~=тх о>² — Я² (ж — х₀) ± mgf, или, обозначив х—х₀ через ξ,

т=— (Я² - теш²)ξ + т(со²х₀ ± gf),

ИЛИ

ii ^{= _ (fc2 _ + ±}

Таким образом получим дифер. ур-ие, аналогичное (28), вследствие чего грузы регулятора будут совершать движение по вышеприведенному закону.

К.д. под действием силы притяжения, пропорциональной расстоянию, при наличии сопротивления, зависящего от скорости. Во многих физическ. явлениях движение тела встречает со стороны среды, в которой движение происходит, сопротивление, являющееся некоторой ф-ией скорости. Самым простым случаем является при этом тот, когда сопротивление среды прямо пропорционально первой степени скорости. Если в частности иметь в виду сопротивление движению со стороны воздуха, то при не слишком больших скоростях с большим или меньшим приближением такая прямая пропорциональность в действительности существует. Еще точнее такая прямая пропорциональная зависимость имеет место при движении магнита около медной массы, встречающего при этом сопротивление движению со стороны индуцированных токов. Если на материальную точку действует кроме силы напряжения F=— Я²ж еще и сила сопротивления среды, пропорциональная скорости v, то есть сила Ф=— αν, где а—фактор пропорциональности между Ф и v, а знак минус указывает, что направление силы Ф противоположно направлению v, то диференциаль-ное ур-ие движения будет:

m ~=- А²ж - αν, (31)

или, обозначая ^ через 2п,

g + 2n§f + fc²as=0. (32)

Если сопротивление среды невелико по сравнению с силою Е, то к > п, что обычно и имеет место. Положив х=е^¹, найдем те значения β, которые удовлетворяют ур-ию (32), а именно:

β=-η± vV-fc², (33)

или, в предположении, что к>п,

β=— η ± iVk²—n²=— n + pi,

где р^У№ — п^г. Отсюда имеем общий интеграл дифер. ур-ия (32):

г - C_lCW + С₂е^ - e "*[C₁e"* + С₂е, (34)

что при помощи формул Эйлера (6) принимает вид:

х=е~^п‘ [Csin pt + С cos pi], (35)

а скорость

v=e~^nt [Ср cos pt — Cp sin pi] —

— ne~^nt [C sin pt + C’ cos pt ]. (35)

Если, при ί =0, ж=0 и ν=ν₀, то

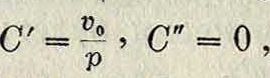
так что ур-ия (35) и (35) принимают следующий частный вид:

ж=ye^-ni sin pi, (36)

v= р e^_nt[pcospi — w sin pi]. (36)

Из (36) следует непосредственно, что движение точки будет колебательное с периодом колебания гр ₌ -^π_ __.

π V

Таким образом К. д. и в этом случае изохронно; однако, в то время как при наличии силы трения период колебания точно такой же, как и при соответствующем свободном гармонич. движении, в рассматриваемом случае период Т меньше периода свободного колебания. Ур-ие (36) отличается от ур-ия гармонического К. д. лишь фактором er^nt. В начале движения, когда время ί еще мало отличается от 0, этот множитель мало отличается от 1, вследствие чего К. д. будет мало отличаться от гармонического; это будет длиться тем дольше, чем сопротивление среды, то есть коэф-т п, меньше. Но по мере увеличения времени ί последующие амплитуды будут все более резко уменьшаться, стремясь к нулю при ί= оо. Очевидно ур-ие (36) дает значения последовательных амплитуд при значе ниях |sinpi|=l, то есть при значениях pt =

Вл ₉ bл _{β β} (2г-1)л

2 ’ 2

Вл

2р ⁹ *

тельные амплитуды будут следовательно:

. (2г — 1)л

2 р у--, или при значениях ί=₂*;. Соответствующие последова-

	ул
А=— е 1 V	2})
	3 пл
2=— е	2 V
2 р	(2Г~1)ПЛ
V0 l.=— е	2 V
’ V

Т. о. последовательные амплитуды составляют геометрическ. убывающую прогрессию со

ЛП

знаменателем, равным е. Такое К. д. называется затухающим. Так как

ЛП

_ ~Ύ

a_r ’

то, взяв натуральный логарифм от обеих частей последнего равенства, получаем:

In a_r+1 — In а_г=— —,

или

1па_г-1па_г+1=™, (37>

так что натуральные логарифмы двух произвольных последовательных амплитуд отличаются на одну и ту же величину, назы-

ваемую логарифмическим декрементом затухания и равную ^π™.

Наблюдая за амплитудами колебания, молено легко определить логарифмическ. декремент затухания, а затем и коэф-ты пи а, определяющие величину торможения среды. Откладывая по оси абсцисс время ί, а по оси ординат соответствующие значения х, получаем графич. изображение (35), представленное на фигуре 10. В технике К. д. с линейным затуханием рассмотренного типа встречается довольно часто. Примером величины, затухающей по приведенному выше закону, может служить напряжение разряжаемого конденсатора, включенного последовательно в цепь вместе с омическим и индуктивным сопротивлениями. Если С—емкость конденсатора, R — омич, сопротивление, L—коэф. самоиндукции, то напряжение ε у клемм конденсатора определяется в ф-ии времени из дифер.ур-ия:

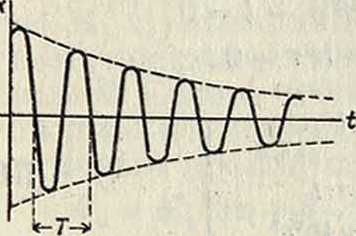
Фигура 10.

d*e R de 1 _пdl‘ + L dt + LC^e=0’

(38)

то есть из дифер. ур-ия, имеющего вид (32). Сравнивая (38) и (32), получаем:

^fc2=xc·

Т. к. выше условием для получения К. д. служило наличие неравенства к>п, то условием для получения колебательного разряда с переменным напряжением ε служит неравенство;

1 _ R 4L г>₂

^или - >Д²·

Если же последнее условие не соблюдено, то разряд апериодический. Все вышеприведенные выводы применимы конечно и к рассматриваемому случаю; так, в частности период колебания разряда равен:

2π 2 л 2д т=-

V Й»-1

V~w-

R‘

4I>

Более сложным случаем затухающего К. д. является тот, когда сила сопротивления среды пропорциональна квадрату скорости. Тогда вместо дифер. уравАения (31) имеем:

т ^d~ + 2тп gf + Г-тх=0. (39)

Рассматривая как нек-рую неизвестную переменную, имеем, интегрируя (39):

1-]ЖТ^г-^т”+^Т <®>

Если начальные условия движения таковы, что, при ί=0, _dl=0, а х=— «₀, то С——e~^tnao (1 + 4ηα₀), так что вместо ур-ия (40) имеем:

dx dt

-/IF

4пж-

-4 П(Ж + Я₀)

(1+4ηα₀)]. (400

Следующую за —а₀ амплитуду а_х получим из (400, приравняв левую часть ур-ия нулю и заменив х через а_х. Таким образом получается трансцендентное уравнение

0 =

=j/~SF [* - - ^е"^4И<“^{1+ β0)}(1 +4ηα₀)], (41)

к-рое м. б. решено относительно а_г лишь методом постепенного подбора значений а_г. Если же разложить правую часть (41) в ряд и отбросить члены, содержащие а₀ или а, в степени выше третьей, то получается следующая приближенная формула:

«ί=«о (l -или в общем виде:

a_r=a_r__x (l — а_г__х). (410

Из (410 видно, что уменьшение амплитуды составляет тем меньшую долю предшествующей амплитуды, чем меньше величина последней. Полный период колебания равен

+ <ь гр _е i* dx

J

[l —4 nx — t

-4Η(Χ + β₀)

(l+4na₀)|

Вынужденные К. д. Если на материальную точку помимо вышеприведенных сил действует еще сила 0, линия действия которой совпадает с линией действия прежних сил и величина которой есть нек-рая периодич. функция времени ί,. то упомянутые выше результирующие движения точки будут этой силой периодически изменяться, вследствие чего сила Θ носит название возмущающей силы. Чаще всего величина силы 0 берется в виде следующей функции от ί: 0=К sin i?f. В зависимости от того, какие из прежних сил F, Q, Т и Ф приложены одновременно к материальной точке помимо 0, могут представиться различные случаи, из которых рассмотрим лишь два следующих. а) Вынужденное К. д. при наличии одной лишь силы притяжения, пропорциональной расстоянию. Если на точку действует кроме 0 лишь одна сила F=—X²x, то дифер. уравнение движения имеет следующий вид: d*x

Ш

dt²

+ λ²Χ=К sin ηί,

(42)

или, если обозначить * через I: + №х— I sin ηΐ.

(43)

Для того чтобы проинтегрировать (43), можно поступить след, обр.: взяв производные два раза по ί от обеих частей (43), то есть

Щ+W^-Wsin (44)

н умножив обе части (43) на η², сложим полученный результат с равенством (44). Тогда получим:

+ №* + П²) % + kWx=0. (45)

Характеристич. ур-ие для дифер. ур-ия (45), то есть ур-ие

ρ⁴ + (7с² -f η²) ρ² + /с²?}²=0, имеет корни ρ=+ ηι и ρ=± Μ. Τ. о. общий интеграл дифер. ур-ия (43) будет

*- С,е+*^г+ С[ e~^vit+ С₂е^+ки + С₂е~^ы,

что может быть при помощи приведенных формул Эйлера (6) представлено еще и в следующем виде:

х=M, sin (pt + γ₂) + А₂ sin (kt + у_а) · (46)

Это и есть ур-ие движения точки в ее результирующем движении. Как видно из (46), результирующее движение состоит из двух составляющих гармонических К. д., а именно: К. д. f₁=4₁sin(iji-Hi), вызываемого наличием возмущающей силы Θ и называемого вынужденным колебанием, и собственного К. д. точки £₂=И₂ sin(kt γ₂), вызываемого наличием силы F. Период первого колебания Т_1; совпадающий с периодом силы Θ, равен ~, а период второго колебания

Т2⁼. Из четырех постоянных ур-ия (46),

А_х, Ул, А₂, γ₂, лишь последние два определяются начальными условиями движения, первые же два определяются из предыдущих данных след, обр.: из (46) имеем:

^=-A₁p²sin(pt]+y₁)-A₂k²sin(kt+y₂)·, (47) подставив (47) и (46) в (43), получаем: А_г (к² - ??²) sin (pt + Ул)=I sin pt.

Так как последнее ур-ие должно удовлетворяться при всех значениях ί и при постоян-ныхПл и Ул, то это требование возможно лишь при Ул=0 иА_г (к²—η²) =1, то есть при Ул=0 и

Ai =. Ур-ия результирующего движе-

ft — Ή

ния (46) и вынужденного движения принимают при этом следующий вид:

х=А₂ sin (kt + у₂) + ~_~i sin pt, (48) ?i=fen^r^sin,?i · (49)

Если период Т₂ возмущающей силы Θ совпадает с периодом Т_г собственных колебаний, то есть если к=р, то, как видно из (48), х принимает бесконечно большое значение. В этом случае говорят, что имеется явление р е-з о н а н с а. Если р становится больше к, то имеет знак, противоположный знаку ξ₂, то есть, другими словами, у свободного и вынужденного колебаний имеется сдвиг фаз, равный половине полного периода. б) Вынужденные К. д. при наличии сопротивления среды. Если на материальную точку, кроме сил F я Θ, действует еще сила сопротивления среды, пропорциональная 1-й степени скорости, то есть сила φ=— αν, то дифер. уравнение движения принимает вид:

^m% + ^aft + №=(50)

ИЛИ

jji-l· 2п ^~ + k²x=l sin ηί. (51)

Т. к. дифер. ур-ие (51) отличается от (32) тем, что в правой части (51) вместо 0 стоит выражение Isinpt, то, найдя частный интеграл (51) и прибавив его к общему интегралу (32), найдем общий интеграл (51). Для этого, положив х=р sin pt -f г cos pt, (52)

найдем такие значения для р и г, к-рые, будучи подставлены в (52), дали бы ж, удовле творяющий (51). Для последней цели имеем из (52):

= рр cos iit—τη sin 7it

d^sx i

OP=— pp²sin pt — τη² COS pt I

что после подстановки в (51) дает:

sin pt (— ρη² — 2nrp + k²p — l) + + COS pt ( — Π?² + 2ηρη + 7{%·)=0,

или

ρη² + 2nrp — к²р + ί=0,

(53)

откуда

rp^z

Ρ =

- 2npp — k²r=0,

2 ΠηΙ

- ηψ~- 4η*η* [

(

(№-η*)· + 4η⁸»7⁸ )

(54)

Общий интеграл принимает при этих значениях р и г следующий вид:

х=e~^nt (С_х sin pt -f С₂ cos pt) +

-(- (p sin pt + r cos pt),

x=e ~^nt A₂ sin (pt + y₂) + A_t sin (pt + yj, (55) причем на основании (И) и (11)

A₂ — VCi + CI‘, Α^Ϋψ + τ²

tgy_a=₅f;

(56)

Из (55) видно, что результирующее движение состоит из одного затухающего колебания с убывающей амплитудою e~^nt-A₂ и вынужденного колебания с амплитудою А_г. Подставляя в (55) значения риг из (54) и произведя необходимые преобразования, получаем следующее значение для последней амплитуды:

1,-. -. ·

V ( ft* -ч“)·+ 4n*/j*

Отсюда, видно, что, по мере приближения значений р к значению к, А_г все возрастает и при резонансе, то есть при р=к, достигает своего максимума, равного ^. Чем меньше при этомп, то естьчемменьшесопротивление среды, тем больше амплитуда A_t. При п=0 мы получаем такой резонанс, как в предшествующем случае при отсутствии силы Ф. Примером для рассмотренного случая колебаний может служить изменение силы тока, протекающего в электрич. цепи, в к-рую последовательно включены: конденсатор емкостью С, индуктивн. сопротивление с коэфициен-том самоиндукции!/, омич, сопротивление R и источник тока с синусоидальным изменением напряжения е=Е sin coi. Дифер. ур-ие изменения силы тока г имеет при этом следующий вид:

ⁱ5F+^Bsf + S^i=i7sincoi>

d*i, R di, 1 · E.,

di* + L df + CL^l~ L ^Sln ’

T. e. получаем дифер. ур-ие, аналогичное (51), так что все полученные выше выводы будут применимы к закону изменения г, если положить

^ ⁼ CL ’l~L

В более общем случае возмущающая сила Θ может быть некоторой произвольной периодич. ф-ией времени ί, такчтодифер. ур-ие (45) принимает вид:

Е(х)=Θ(ί), (57)

где Е(х) представляет собой левую часть ур-ия (42), a 0(f) данную функцию Θ. Если θ(<) есть сумма периодич. функций времени 6,(t)i 6₂(0, ···, 0«(ί), то, найдя частные интегралы 1_1г 1._г, ., 1_пиз дифер. ур-ий Е{х)==θ,(ί); E(x)=d.£t) E(sfi=e,"(t), получим общий интеграл уравнения (57) в виде I — =!χ + ί₂ +. + 1„, что и определяет сложное К. д., вызванное одновременным действием эластичной силы F и данной периодич. силы Θ. Если в частности х^аждая из составляющих периодическ. сил 0 имеет вид, аналогичный правой части (42), то есть

θ_ν=>Κ_νsini7„i .(»-1,2,., η), (58) то соответствующий интеграл 1_Г имеет вид, аналогичный (46), то есть

X - A_v sin (η_νί + γ_ν) + A_r (kj + γ_ν), что показывает, что каждая из составляю-хцих сил 0_Г будет вызывать нек-рое вынужденное колебание A_v sin (η_ν1 + γ_ν).

Исследование К. д. упругих тел (в частности частей машин или тел, соединенных с последними), находящихся под воздействием

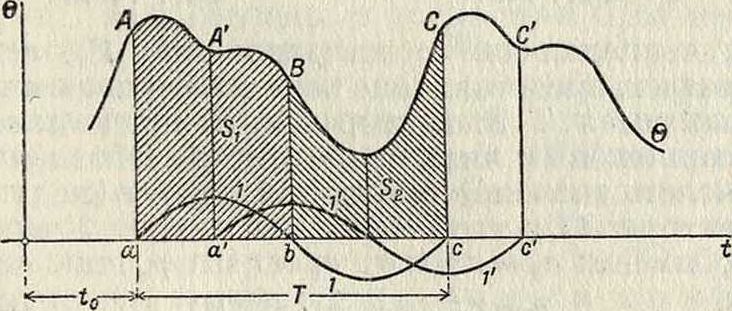
периодич. сил, имеет во многих областях техники громадное значение (вибрации поршневых двигателей, колебания мостов, колебания фундаме1Гтов машин и тому подобное.). Допустим, что кривая АВС (фигура 11) есть периодич. кривая, выражающая функциональную зависимость Θ от ί, причем У=ав есть период полного изменения силы б. Пусть, далее, сила б действует на упругое тело (или на часть нек-рого упругого тела), имеющее период собственных колебаний, равный также Т. Площадь S, ограниченная частью АВС хсривой, ординатами Аа и Сс и осью абсцисс, представляет собою полный импульс силы Θ в промежутке от ί=ί₀ до ί=ί₀+Τ, то есть ί + т

s= 7 ^θ<ί)-

ί.

Рассматриваемое упругое тело может под действием силы б совершать гармоническое К. д., представленное синусоидой 1, с периодом=У, поглотить при этом импульс силы, равный разности площадей δχ—£„, где Si—площадь, ограниченная частью АВ кривой, ординатой Аа, ординатой ВЬ, проходя щей через середину b отрезка ав, и осью абсцисс, a S_t—аналогичная площадь ВСсЬ. Уравнение кривой 1 может быть представлено в виде:

А=А_г (sin rj_Lt+=А_х sin (а + у_г) =

= Их sin [|г(«-<₀)] · (59)

Сдвинув ординаты Аа и В b на четверть периода, найдем аналогичным способом новую кривую 1’ возможного гармонического К. д. тела с тем же периодом У, но имеющего ур-ие

A=A sin + ζ·+ Ух)=Ai cos (a + y_x) -

= ^isinp(H-f-io)]. (60)

Результирующее же К. д. будет иметь ур-ие Р=A sin (α + ух) + А[ cos (α + Ух), (61) что может быть приведено к виду:

Р =- Pi sin (α + у(). (62)

Так. обр. из данной периодич. кривой б м. б. выделено в зависимости от Ух или ί₀ какое угодно число гармонии, кривых (гармоник) периода У, выражающих возможные колебания упругого тела. При нек-ром определенном значении у_х амплитуды Д_х и А_г достигнут максимальных размеров, что будет иметь место при равенстве ординат, проходящих через <₀ и ί₀ -f У/2. Махссимальная величина Рх определяется равенством:

Р ~А + А*.

max ^lmax ^lmax

Вычитая далее из ординат данной кривой б соответствующие ординаты гармония. кривой!, получим новую периодич. кривую Θ, выражающую остаточную периодичеи“. силу, которая может в свою очередь вызвать К. д. 2, определяемое так же, как и выше.

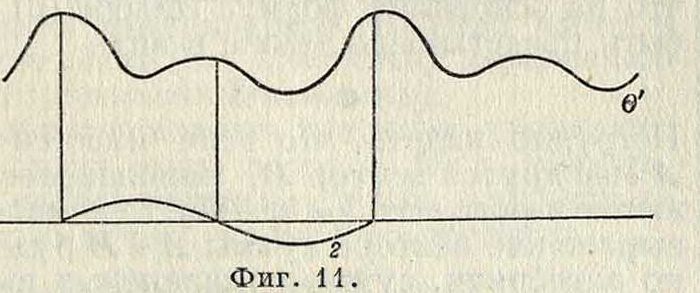
Данная периодич. сила б может вызвать также гармонии, колебания с периодомУ/2. Для выделения соответствующей кривой 2 (фигура 12) разделим ас=Т на четыре равные части и, проведя через точки деления ординаты, разделим площадь S на четыре части δχ, S₂, S₃, S_t. К. д. 2 поглощает импульс

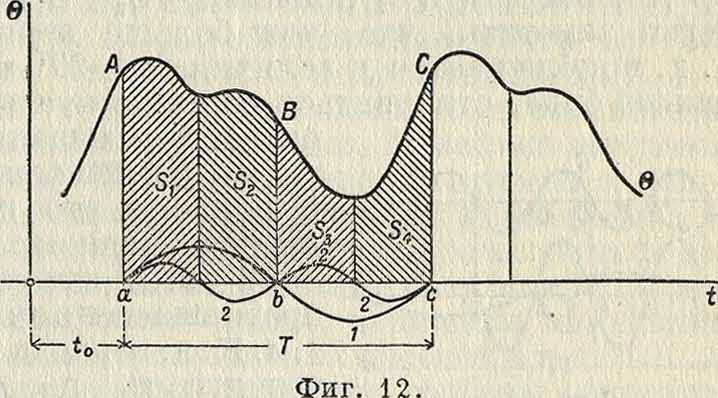
силы, равный разности площадей (S₁ + S₃) — — (S₂ -j- S₄), а уравнение кривой 2 будет иметь вид, аналогичный (59), а именно:

А=А₂ sin 2 (а + у₂)=-4₂ sin

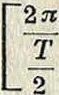
(63)

Передвинув затем ординаты на четверть периода, получим еще одно возможное К. д. с периодом У/2, уравнение которого будет: A=A cos 2 (а + у₂). (64)

Ур-ие же результирующей кривой с периодом У/2 будет:

Р=А₂ sin 2(а + у₂) + Д cos 2(а + у₈) =

= Р_г sin 2 (α-f γ₂). (65)

Как и выше, в зависимости от у₂ м. б. выделено любое число К. д. с периодом Т/2.

Обобщая сделанные выводы, можно прийти к заключению, что данная периодич. сила Θ может в упругом теле вызвать любое число К. д. с периодами где и=1,2, 3,., причем уравнения кривых К. д. имеют вид: Р=А„ sin η (а + у_п) + Ап cos п (а + у_и) =

= Р_п sin п(а + γί,). (66)

При аналитич. исследовании вопросов, связанных со сложными периодич. К. д., особенно крупное значение имеет разложение данной периодич. функции в ряд Фурье, основывающееся на том, что всякая периодич. ф-ия /(f), не имеющая в интервале 2π бесконечно много максимумов и минимумов и принимающая бесконечно большие значе-

+ π

ния, сохраняя конечной площадь Jf(t)dt,

— π

м. б. представлена рядом:

СО

А₀ + 2 C_nsinw(a>f + у) +

71=1

СО

+ 2 D„cosn(cot +у).

п=1

Об аналитич., графич. и механич. способах разложения /(f) см. Фурье теорема и Гармонический анализ.

Нетрудно видеть, что сила, изменяющаяся по закону какой-либо периодич. кривой периода Т, не может вызвать колебаний с периодами 2 Т, 4 Т, бТит. д. В самом деле: возьмем для простоты синусоидальную периодическую силу Θ, имеющую период Т=ас (фигура 13). Очевидно, сила Θ может вызвать колебание того же периода Т, причем К. д. поглотит импульс, равный разности площадей iS_l — S₂. Взяв для К. д. период ас’> ас и разделив его в точке b пополам, получим, проведя соответствующие ординаты ВЬ и Сс, площади Sx и S₂, причем S(—S₂ < S₂.

Легко заметить, что, чем больше период К. д. приближается к величине ае=2Т, тем меньше будет становиться соответствующая разность площадей, то есть поглощаемый импульс, и что при периоде, равном «6==2Т, этот импульс превращается в нуль, то есть К. д. периода 2Т возникнуть не может, точно так же, как и периодов 4Т, 6Т и т. д. Наоборот, при периоде, равном 3Т, 5Т и т. д., разность площадей £>χ —S₂, вместе с тем и поглощаемый К. д. импульс, достигают своего максимума. На основании этих соображений пе-риодическ. сила θ(ί) периода Т может быть разложена в следующий ряд Фурье:

СО

^e(t)=(^An- ^A3n~l А_5п—.) sin n(cot + у) +

71=1

СО

+ 2(А_п—* Аз_п - I А_ъп- .) cos n(a>t + у), п= 1 * ⁰

где А_п, А_зп,., А’_п, А_зп,. .суть амплитуды тех К. д. порядков п, 3п, 5и,., которые м. б. вызваны в упругом теле силой 6(f).

В е к т о р н о-к омплексный способ представления К. д. Кроме аналитич. и графическ. способов представления К. д. существует еще векторно-комплекс-н ы и способ представления их, заключающийся в основном в следующем. Допустим, что в плоскости, проходящей через два взаимно перпендикулярных компланарных вектора Т^и F₂ (фигура 14а) имеется еще вектор А, проекции которого по направлениям FjH F₂cyrb «! и α₂. Пусть ось 1, совпадающая с направлением F_lt есть графич. представление всех действительных чисел, а ось

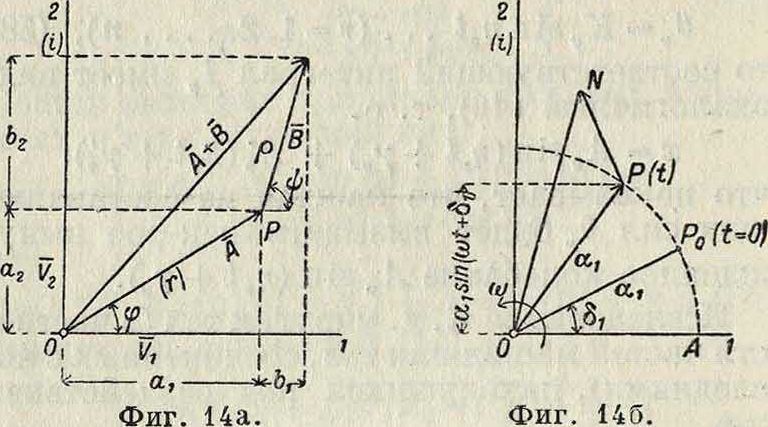
2, совпадающая с направлением F₂, есть графич. представление всех возможных мнимых чисел. Т. о. вектор 4 метров б. представлен комплексным числом а=а₁ + а.₂г. Обозначая числен, значение вектора А через г (модуль вектора А), а угол между А и осью 1 через φ, имеем: а_г=г cos<p, ft₂=rsin?>, так что a=r (cos <р + i sin ψ), (67)

что на основании формул Эйлера (6) может быть представлено также в виде

a=re^i<p. (68)

Нетрудно видеть, что если имеется кроме А еще другой вектор Б, комплексное выражение которого есть b=b₁ + if)₂,TO комплексное выражение вектора суммы А+Б будет равно алгебраич. сумме комплексных выражений слагаемых векторов, то есть равно а+Ь== (αχ + Ьх)+г(а₂ Ь₂). Если b представить в виде b=ρ е^{г ψ}, то алгебраическ. произведение аЬ представит новый вектор αϋ=νρβ^ι(·^φ+ψ модуль которого равен τρ, а угол, образованный им с осью 1, равен φ-{-ψ· Если в частности у=0, то вектор а при умножении лишь удлиняется в ρ раз, сохраняя свое направление, если же ρ=ί, то вектор поворачивается лишь на угол ψ, сохраняя свою величину. В более общем случае имеем:

а^т _ /*^m(cos ту + i sin mq>). (69)

Рассмотренный способ изображения векторов удобен при исследовании периодическ. колебаний, разлагаемых в ряд Фурье. Основное колебание ξχ=αχ sin (cof + (5_t) м. б. представлено след, образ.: отрезок ОР=а_г(фигура 146) вращается с постоянною угловою скоростью ω вокруг О, так что в момент f угол между ОР и осью 1 равен tuf+dj, если в момент f =0 вращающийся отрезок отстоял от оси 1 на угол <5j. Проекция же ОР на ось 2 равна а_г sin (ωί+<5,). Так. обр. колебание ξχ может рассматриваться как изменение мни-

Фигура 13.

мой части вектора, представленного комплексным числом а_ге^г(“‘^+ад. Другое, синхронное с первым, колебание *ι=sin (со i+yj)

может быть также представлено как изменение мнимой части комплексного числа

β₁β^ι(·^{ω1 + Υι} представляющего нек-рый другой вектор. Сумма рассматриваемых двух колебаний а_х sin (со i + <5j) + β₁ sin (со t + γβ) может т. о. рассматриваться как новое результирующее колебание, представленное изменением мнимой части комплексн. числа i(o)i +<5,)

а,е

Если ОР есть вектор, представленный первым комплексным числом, a PN—вектор·, представленный вторым, то ON=PN+OP

есть вектор, представленный ае^{г1ш1 + ь} так что весь процесс сложения двух данных колебаний м. б. рассматриваем как изменение проекции вращающегося с постоянною угловою скоростью со около О треугольника ΟΡΝ на ось мнимых количеств. Если составляющие колебания синхронны, то множитель е^гш4 м. б. опущен, и тогда тр-к ΟΡΝ неподвижен в пространстве. Чтобы получить мгновенные значения как слагаемых, так и результирующего колебаний, нужно проектировать неподвижный тр-к ΟΡΝ на прямую, вращающуюся около О с постоянною угловою скоростью — со, то есть в обратном по отношению к первому направлению. Т. обр. получается т. наз. диаграмма к о л е-б а н и й. Диаграммы колебаний более сложных видов применяются особенно часто в электротехнике (смотрите Генератор переменного тока, Индукционные машины).

Как легко усмотреть,все дифер. уравнения разобранных выше случаев К. д. представляют собою частные случаи следующего линейного дифер. ур-ия 2-го порядка:

Л₀(х,t) ~ + Л_г(х, t) f +A₂(x,t)х +

+A₃(x,t)=О, (70)

где коэфициенты А_а, A_lt А₂ и А_г—ф-ии от х и t. Во всех рассмотренных выше случаях эти коэф-ты были величинами постоянными. При А₁=А₃= 0 получается вид дифер. ур-ия (4), при A_s= 0 получается вид дифер. ур-ия (31) и т. д. При более сложных случаях К. д. получаются однако дифер. ур-ия более общего вида (70). Аналитич. методы интегрирования дифер. ур-ий вида (70) довольно сложны и потому для практич. надобностей весьма мало пригодны. Гораздо более быстрые результаты с достаточной для практики степенью точности дают графические методы интегрирования дифер. ур-ий, приводимых к рассматриваемому виду или даже к еще более общему виду:

О-⁰·

лишь бы последние были разрешимы отно-d^zx

сительно

dt^%

d^zx

di* ^:

представляемы в виде:

(dx dt

t(% *.<)·

(71)

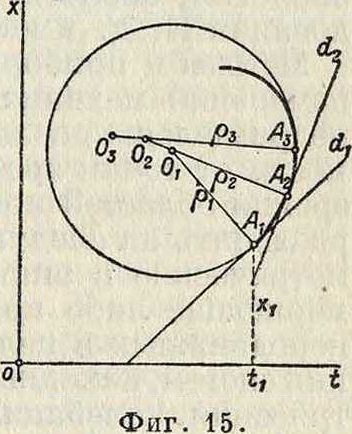
Из графич. методов интегрирования дифер. ур-ий рассматриваемых видов укажем в общих чертах на следующий метод. Пусть имеются следующие начальные условия движения точки: при ί=ί_χ, х=х_х и v — v_lt то есть

2У=х[. По отношению к двум взаимно перпендикулярным осям х и ί (фигура 15) эти начальные условия движения определяют некоторую точку А_г и нек-рое направление А_г. Из ур-ия (71) имеем:

х{=(х’у, *i, к),

а из известного соотношения

О ₌ i/(!+*·>’,

* х"

где ρ — радиус кривизны кривой х=x(t), имеем радиус кривизны ρ_χ искомой кривой в точке А_г, а именно:

V (i+x;^a)³

^ρ>×"

Зная ρ_τ и направление d_lt найдем соответствующий центр кривизны O_v т. к. 0₁А₁=перпендикулярен к d_v Проведя из О_г радиусом ρι соприкасающуюся окружность и взяв на этой же окружности достаточно малую дугу А_гА₂, получим точку А₂, которая приблизительно будет находиться на искомой кривой и которой будут соответствовать новые значения х₂ и ί₂ и новое направление х₂. Поступая по отношению к точке А₂ точно так же, как и по отношению к А_г, получим новую точку А₃, и т. д.Т. о. можно искомую кривую×= x(t) определить с любой степенью точности как состоящую из отдельных малых дуг, принадлежащих различным соприкасающимся окружностям.

К.д. в различных областях техники. К. д., обнимающие почти все области техники, м. б. подразделены на К. д. с одной степенью свободы и К. д. со многими степенями свободы (смотрите Механика теоретическая). К первой категории относятся например колебания фундаментов под влиянием К.д. машин, колебания быстро вращающихся валов, колебания кручения быстро и медленно вращающихся валов, движения автоматич. клапанов в поршневых насосах и т. д. К К. д. с несколькими степенями свободы относятся например колебания двойных маятников, центробежных регуляторов, маятниковых тахометров, инерционных регуляторов, турбинных регуляторных систем, рулевых механизмов судов и тому подобное. Исследования К.д. имеют особенно существенное значение при движении судов, паровозов, аэропланов, при явлениях движения волчков, при исследовании жироскопич. сил и т. д. В теории упругости особенно важное значение имеет исследование колебаний струн, эластичных пластин (мембран), продольных и поперечных колебаний стержней. В строительном деле исследуются вопросы, связанные с колебаниями мостов, фундаментов, башен, маяков

и тому подобное. В областях, связанных с исследованием деталей машин, рассматриваются колебания различных пружин и рессор. Большую роль играет исследование К. д. в гидравлике, в особенности при установлении законов движения волн и образования вихрей, движения жидкости в трубопроводах и в сообщающихся сосудах и в частности в гидравлич. машинах и тому подобное. Крупное прикладное значение имеет исследование колебаний пара в соплах паровых турбин. Аналогичные проблемы возникают при исследовании законов движения газов и паров в трубопроводах. Фундаментальное значение имеют К. д.в акустике, базирующейся целиком на установлении законов К.д. воздушной среды. С этими же проблемами связаны и вопросы строительной акустики, теории музыки, конструирования музыкальных и акустических инструментов и тому подобное. Громадная область прикладной и теоретич. электротехники, теория электромагнитных колебаний, теории квант и новейших статистич. и волновой механики целиком базируются на исследовании вопросов, связанных с видом К. д., и наконец в таких областях, как физиология, биология и метеорология, исследования К. д. имеют крупное значение.

Методы и приборы для непосредственных измерений механических К. д. могут быть подразделены различным образом в зависимости от точки зрения. Так например с точки зрения областей применения их можно подразделить на следующие группы: 1) сейсмометрические в широком смысле слова—измеряющие либо колебания эластичных, но неподвижных в целом систем, либо колебания систем, находящихся в движении (землетрясения, колебания почвы, колебания фундаментов машин, колебания судов, мостов, ферм, К. д. поездов, аэропланов и тому подобное.);

2) измеряющие переменные механич. воздействия (напряжения в частях мостов, судов, аэропланов, кручение валов и тому подобное.);

3) индикаторные (индикаторы паровых ма

шин и двигателей внутрен. сгорания, измерения колебательных давлений жидкостей и газов и тому подобное.); 4) приборы общего машиностроения (техника синхронизирования, равномерность хода ременных и зубчатых передач и тому подобное.); 5) акустические—связанные с измерением звуковых колебаний; 6) физиологические и биологические—измеряющие колебания в живых организмах. По роду регистрации К. д. их можно подразделить на механически, оптически и электрически регистрирующие. К сейсмометрическим приборам, в" широком смысле слова, принадлежат в первую очередь приборы, измеряющие колебания почвы: сейсмографы и клинографы (смотрите Сейсмология).

Для измерения колебаний судов применяется паллограф О. Шлика, конструкция которого в основе состоит из следующих частей: 1) приспособления, регистрирующего вертикальные колебания, 2) приспособления, регистрирующего горизонтальные колебания, 3) часового механизма, приводящего в движение цилиндр с полоской бумаги и отмечающего на ней промежутки времени, и 4) регистрирующей части. Схема упомянутого паллографа О. Шлика предста влена на фигуре 16. Горизонтальные колебания судна вызывают колебания горизонтального маятника М_г, а вертикальные—колебания вертикального маятника М₂ (смотрите Маятник). Относительные смещения грузов маятников передаются при помощи системы рычажков пишущим штифтам А я В, наносящим соответствующие кривые на полоску бумаги, приводящейся в движение цилиндром К при помощи часового механизма С. Третий штифт D, находящийся под воздействием часового механизма С_г, отмечает на полоске бумаги интервалы времени. Так как маятники наряду с вынужденными колебаниями имеют еще и собственные периоды колебаний, могущие исказить истинный характер регистрированных колебаний, то особенно важно придать прибору такую конструкцию, при которой достигались бы по

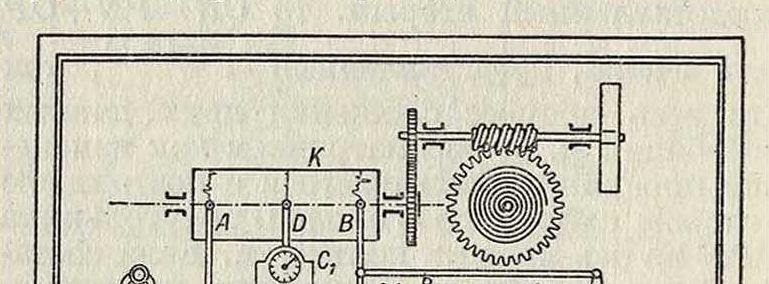
Фигура 16.

возможности значительные периоды собственных колебаний, и иметь кроме того возможность регулировать эти колебания. У вертикального маятника первая цель достигается след, образом. Маятник, вращающийся около оси S, опирается в точке Е на конец вертикальной пружины F, причем точка Е лежит ниже обычного горизонтального положения оси стержня маятника. В зависимости от расстояния точки Е от оси стержня м. б. получен больший или меньший период собственных колебаний. В паллографе точка опоры Е м. б. смещена в желаемом направлении. Вертикальный маятник паллографа снабжен двумя пружинами F и Г¹, соединенными рычагом В с целью уменьшения вертикальных размеров прибора и возможности случайных смещений оси пружины. Обычная частота колебаний вертикального маятника прибора Шлика равна 20 в минуту; при этом прибор в состоянии правильно регистрировать колебания с частотой до 40 в мин. Горизонтальный маятник состоит из тяжелого металлическ. цилиндра (фигура 17), подвешенного горизонтальной своей осью ζζ к двум стержням huh. могущим перемещаться во втулках Ь и b. С другой стороны, эти стержни могут вращаться на цапфах, укрепленных на стержнях а, а. Втулки 6, 6 соединены между собой горизонтальным стержнем, могущим вращаться вокруг оси d. Последняя при помощи конич. зубчаток к, к может приподниматься или опускаться. Период собственных колебаний Т горизонтального маятника зависит от величины Я=р + q — г, где р—рас-

стояние от оси вращения d до оси ее, q—расстояние от цапфы вдоль стержня h до оси zz, г—длина стержней а, причем при Н= О период Т становится бесконечно большим. Изменяя указанным способом величину р,

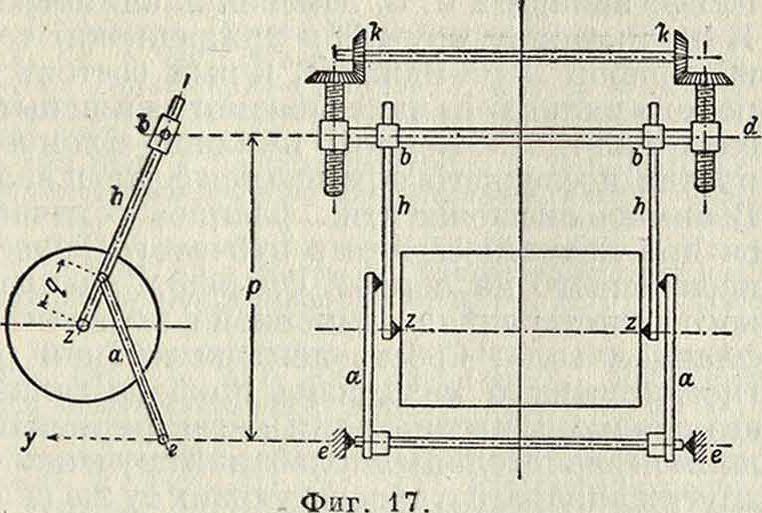
можно изменять и величину Т. В приборе Шлика (фирмы Н. Maihak, Hamburg) м. б. достигнут период колебаний горизонтального маятника до 1,25 ск.

Измерители колебаний Шенка сконструированы отдельно для горизонтальных и вертикальных колебаний. На фигуре 18 представлен измеритель вертикальных колебаний Шенка (фирмы Karl Schenk, Darmstadt). В основном прибор состоит из рычага а, снабженного грузом Ь и притягиваемого пружиною с натяжение которой м. б. желаемым образом отрегулировано. Подшипник маятникового рычага, находящийся в d, сконструирован так, что позволяет вращаться рычагу почти без трения. Для аннулирования вредного влияния собствен, колебаний маятника имеется в е жидкостное амортизирующее приспособление, вследствие чего собственные колебания маятника почти апериодич-ны. Наблюдения за колебаниями производятся непосредственно при помощи вращающегося зеркальца /, соединенного со стержнем а при помощи легкой алюминиевой рычажной системы От источника к падает на

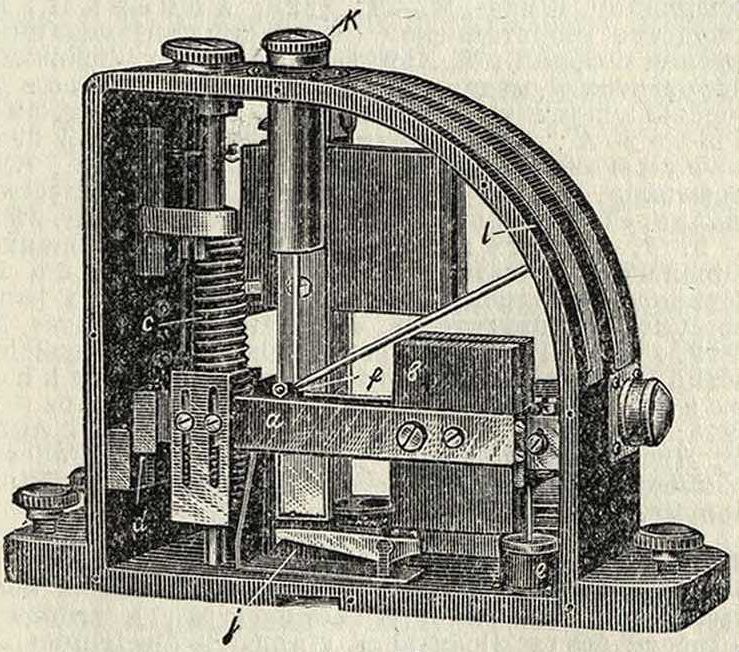
Фигура 18.

зеркальце световой луч, отражаемый на прозрачную шкалу Ϊ. При отсутствии колебаний луч отмечается на нулевом делении шкалы светящейся точкой; при наличии же регистрируемых колебаний получается вместо точки светящаяся полоса, середина которой находится на нулевом делении шкалы. Аналогичную конструкцию имеет измеритель Шлика для горизонтальных колебаний. В новейшем измерителе колебаний Майгака система подвеса тяжелой массы так сконструирована, что получается маятник, в котором скомбинированы свойства как горизонтального, так и вертикального маятников. При помощи этого измерителя колебаний имеется возможность регистрировать колебания, происходящие в любой плоскости, для чего весь прибор вместе с регистрирующей частью может быть повернут либо вокруг своей продольн. оси либо вокруг вертикальной оси. Частота собственных колебаний может быть отрегулирована в пределах от 15 до 65 в минуту.

Целый ряд измерителей колебаний, которые не совсем правильно называют измерителями ускорений, пользуются в основном вместо маятников плоскими эластичными пластинками, закрепленными одним своим концом и снабженными на другом конце привеском (измерители колебаний Голицына, Майгака и др.). В частности к таким приборам принадлежит измеритель колебаний Коллина (фирмы Cambridge Instrument Со.),к-рый, подобно измерителю Майгака, способен в зависимости от своего положения измерять колебания, происходящие как в горизонтальной, так и в вертикальной плоскостях. Однако вследствие большой частоты собственных колебаний и сравнительно небольшой чувствительности аппарат может применяться лишь при регистрации больших колебаний, например колебаний вагонов. В зависимости от этого обстоятельства аппарат должен, в отличие от предыдущих аппаратов, не увеличивать амплитуды регистрируемых колебаний, а уменьшать их, чтобы быть в состоянии зарегистрировать их на полоске бумаги. Для регистрации же небольших колебаний аппарат Коллина непригоден. Особенным удобством, портативностью и достаточной для практич. целей точностью обладает виброграф Гейгера (фирмы Lehmann & Michels, Hamburg), к-рый может применяться для измерения самых разнообразных колебательных движений. Основная его часть состоит либо из полого тяжелого кольца, либо из тяжелогокольцево- фигура i9.

го сегмента, к-рый при помощи шарикового подшипника может вращаться вокруг нек-рого стержня(фигура 19). Этот сегмент при помощи спиральной пружины соединен со шкивом, могущим также вращаться вокруг оси стержня на шариковом подшипнике. При свободном шкиве и полом кольце он служит как торсиограф для целей измерения колебаний кручения валов. При скрепленных же с валом или с кожухом шкиве и кольц. сегменте аппарат может служить в качестве горизонтального или вертикального маятника,то есть может быть приспособлен для измерений как горизонтальных, так и вертикальных колебаний (фигура 20). Тангенциальные смещения тяжелого кольцевого сегмента по отношению к

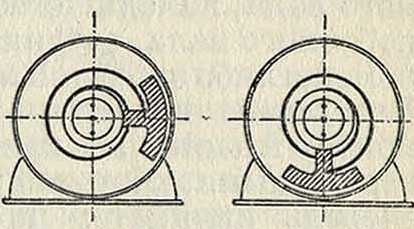
шкиву передаются при помощи системы ломаных рычажков в радиальном и аксиальном направлениях, где и регистрируются. Для достижения возможно большего периода собственных колебаний необходимо, чтобы тяжелый сегмент имел возможно больший по отношению к оси вращения момент инерции и чтобы ц. т. его был по возможности близок к оси вращения. Верхний предел частоты колебаний, регистрируемых аппаратом Гейгера, достигает 50 000—60 000 в мин. Низший предел амплитуд колебаний, регистрируемых прибором равен 0,05 миллиметров. Аппарат

м. б. укреплен в любом положении и может измерять колебания в любой плоскости. Из многочисленных конструкций измерителей колебаний, принадлежащих к рассматриваемой категории, следует упомянуть еще измеритель колебаний Гехлера, использующий горизонтальный маятник.

К. другой группе принадлежат аппараты, измеряющие периодич. изменения сил и напряжений материалов, причем собственно измеряются не силы и напряжения, а сдвиги и кручения, происходящие, в испытуемом материале, и лишь по их величине судят о величине первых. К механич. индикаторам кручения принадлежит например индикатор кручения Колли, измеряющий кручение не самого вала, находящегося под испытанием, а побочного вала, соединенного с первым при помощи либо зубчатой либо цепной передачи. Вследствие целого ряда недостатков этот прибор в настоящее время вытеснен более совершенными, к которым принадлежит в первую очередь индикатор кручения Феттингера, схема которого вполне аналогична схеме крутильного динамометра (смотрите). Частота собственных колебаний аппарата зависит от упругих свойств материала полого цилиндра и может при подходящем выборе материала достичь желаемой величины. Недостатком аппарата является наличие центробежных сил, развивающихся при колебаниях во всей системе рычагов и могущих до некоторой степени исказить истинный характер колебаний или отдалить пишущий штифт от регистрационного цилиндра. Однако в новейших конструкциях этот недостаток устранен: регистрирующий рычаг сконструирован так, что именно центробежная сила прижимает штифт к цилиндру. Новейшие конструкции попутно устраняют еще и другой недостаток аппарата, заключавшийся в том, что при из мерении колебаний кручения валов больших диаметров требовалась полоса бумаги значительной длины, скорость движения которой доходила до 2 м/с·к. Для целей, встречающихся в практике судостроения, пишущий штифт аппарата м. б. заменен планиметром. К индикаторам кручения принадлежит также прибор Дени-Эджком, к-рый состоит из полого цилиндра, натягиваемого на испытуемый вал и снабженного на конце фланцем; против последнего помещается фланец вала. Взаимное смещение этих фланцев отмечается при помощи сегмента зубчатого колеса, насаженного на первый фланец и сцепленного с шестерней, соединенной с подвижным фланцем вала. Собственные колебания регистрирующего механизма прибора делают его однако пригодным для регистрирования лишь незначительных колебаний кручения. В других аппаратах, преследующих ту же цель, заменяют полый цилиндр либо диском, насаживаемым на вал (аппарат Нетмана), либо валом, вставленным в цилиндрич. полость, просверленную в самом валу в аксиальном направлении. Кроме этих непосредственных измерителей колебаний кручения имеется для той же цели целый ряд оптич. аппаратов, в которых применены либо неподвижные отражающие зеркала и призмы (Фивег и Вет-гаузер, Баурсфельд) либо вращающиеся зеркала (стробоскопические аппараты Амслера, Фивега и др.). Другие аппараты используют одновременно как механические, так и оптические методы измерения и регистрации колебаний кручения (Дени-Эджком, Гоп-кинсон и Тринг и др.). Наконец в большом количестве аппаратов использованы для рассматриваемой цели электромагнитные методы (приборы Дени и Джонсона, Вебба, Гольдшмита, Нетмана, Мулена, Форда и др.). Об аппаратах, регистрирующих колебания при растяжении и изгибе, а также об аппаратах других групп, из числа перечисленных выше, имеются подробности в соответствующей специальной литературе.

Лит.: Тимошенко С., Курс сопротивления материалов, 6 изд., М,—Л., 1928; Аппель П., Руководство теоретической (рациональной) механики, перевод с франц., М., 1911; Сомов П., Основания теоретической механики, СПВ, 1904; Суслов Г., Основы аналитической механики, 2 нзд., Киев, 1911; Яшнов А., Курс аналитич. механики, М., 1925; Бастамов С., Бончковский В. и до., Курс геофизики, М., 1924; Мартенс Л., Гармонический анализ, «Технико-экономический вестник», М., 1925, т. 5, 2; Мартенс Л., К вопросу о вибрациях поршневых двигателей, М., 1925; Брянцев П., К вопросу о явлениях резонанса в коленчатых валах авиационных двигателей, «Техника возд. флота», М., 1929, 7 и 8; Н о rt W., Technische Schwingungslehre, Berlin, 1922 (обшионая библиография); Forchhei-mer Ph., Grundriss d. I-Iydraulik, 2 Aufl., Lpz.—B., 1926; В r e i s i g F., Theoretische Telegrapliie, 2 Aufla-ge, Braunschwdg, 1924; de Brogli L., Ondes et mouvements, Paris, 1928; Timoshenko S., Vibration Problems in Engineering, N. Y., 1928; Nowa-k о w s k y, Harmonische Analyse, «Ztschr. t. angewan. Math. u. Mech.», Berlin, 1927, p. 501; Blaess V., Uber Sehwingungen v. Maschinenfundamente u. deren Beseitigung, B., 1928; В Ion del M., A. propos de la th6orie des oscillographcs. «Industrie 61ectrique», P., 1929; T li о m a H., Aufzeichnung sehnell.r Sehwin-gungen, «Z. d. VDI», 1929, 19; Wichert A., Theorie d. Schuttelschwingungen u. Ontersuchung d. Schiit-telersclieinungen von elektr. Loki motiven, B., 1924; Miller M., Die Wcllen, die Sehwingungen u. die Naturkrafte, Brschw., 1927; Casper L., Einfuhrung in die komnlexe Behandlung ven Wechselstromauf-gab»n, B., 1929; Ring H., Die symbolische Methode zur LOsung von Wechselstromaufgaben, 2 Auflage, B., 1928; Maschinen u. Fundamentschwingungen, Yerlag

VDEW, Berlin, 1929; Steuding H., Messung mechanischer Schwingungen, Brschw., 1928; R a t h-1 о ii e Th., Unusual Vibration of a 25000 kW Turbine, «Electrical Journal», Pittsburg, 19 18, 2, p. 89; Ratlilone Th., Curing Resonant Vibration in Turbine Units, «Power», New York. 1928, 15, p. 629; Iiathlone Th., Vibration of Turbine-Foundations, «Power», New York, 1928, 15, p. 588; Vibration in Steam Turbines, «Power Plant Engineering». Chicago, 1929, 11, p. 662; Vibro-Damper designed to Deaden Machine Vibration, ibid., 1927, 15, p. 856; D о h m e, Modern Steam Turbine-Foundations, «Power», New York. 1927, 5, p. 187; Zech T., Harminische Analyse mit Hilfe d. Lochkartenverfahrens. Zeitschrift fur angewandte Mathematik und Mechanik, Berlin, 1929, B. 10, Η. 1 5, p. 425; L о hm a η n W., Die Hermann-schen Schablonen zur harmon. Analyse, ibid., 1922, B. 2, p. 153; Stodola A., Drehschwingungen von Mehrkurbelwellen, ibidem, 1929, B. 10, H. 5. p. 349; Stumpf C., Die Sprachlaute, B., 1926; Wagner K., Der Frequenzbereich von Sprache und Musik, «ETZ», 1924, p. 451; Schneider E., Matliema-tische Schwingungslehre, Berlin, 1924; Fbppl O., Drehschwingungs-Dampfungsfestigkeit von Baustoffen, «Beitriige zur technischen Mechanik u. teehnischen Physik), B., 1924; DreyfusL., Eigenschwingungen von Systemen mit periodischer Elastizitat. ibid., B., 1924; Fop pi O., Grundziige d. techn. Schwingungslehre, B. 1923; Geiger J., Mechanisehe Sehwingun-gen u. ihre Messung, B., 1927. M. Серебренников.