 > Техника, страница 54 > Комплексные числа
> Техника, страница 54 > Комплексные числа
Комплексные числа
Комплексные числа, числа вида а + Ы, где а и b—действительные числа (положительные или отрицательные и в частности м. б. нулями), г—м нимая единица, удовлетворяющая ур-ию: г2=— 1, что обычно выражается так: i=V—1. Очевидно ΐ3=— г, г4=1, г5=г,.·· Действительные числа являются частным случаем К. ч., когда Ь= 0; если же «=0 и Ьф0, то получаем чисто мнимое число Ы; К. ч. есть нуль, если а= 0; а называется действительной частью К. ч.; Ьг—мнимой частью, b— коэфициентом при мнимой части. Два К. ч. равны, если равны действительные части и коэфициенты при мнимых. Два К. ч., отличающиеся лишь знаком при мнимой части, а + Ы и а — Ы, называются сопряженными. Часто К. ч. изображается одной буквой: а + bi=z.
Геометрическая интерпретация К.ч. Берем систему прямоугольных декартовых координат на плоскости; называем ось абсцисс действит. осью, ось ординат— мнимою; изображаем К. ч., а + Ы, точкой М с координатами (а,b) или вектором ОМ. Если введем на плоскости полярные координаты a=r cosy, b=rsin<p, то К. ч. примет вид: α-f- Ы= г (cosy.+ i sin<p) (тригонометрия, форма К. ч.); г=+ γα2 + b2 называется м о-дулем К. ч.; он выражает длину вектора ОМ и изображается символом |а + Ьг[; угол φ называется аргументом К.ч. Положительные действительные числа имеют аргумент 0, отрицательные π; аргумент определяется не однозначно, а с точностью до слагаемого 2кл (где к—любое целое число), т. к. от прибавления целого числа окружностей значения cos?> и sin φ не изменяются. Сопряженные К. ч. имеют равные модули и противоположные аргументы.
Сложение двух К. ч. а + Ы и а + bi совершается по правилу:
(а + Ы) + (а + bг)=(а + а) + г (b + b). Геометрически сумма представится диагональю параллелограмма, построенного на векторах, изображающих слагаемые (фигура 1).
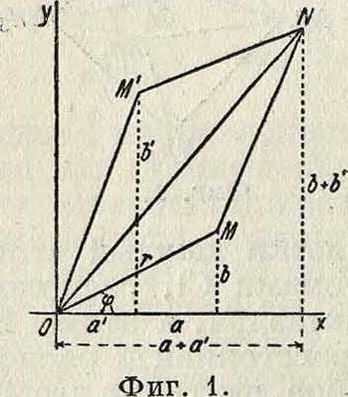
Сложение векторов на плоскости—см. Векторное исчисление. Сумма сопряженных чисел равна (а + Ы) + (а — Ьг)=2а,—действительному числу. Из геометрическ. интерпретации (сторона треугольника меньше суммы двух других сторон) следует: модуль суммы ^ сумме модулей.
Вычитание К. ч. дается ф-лой:
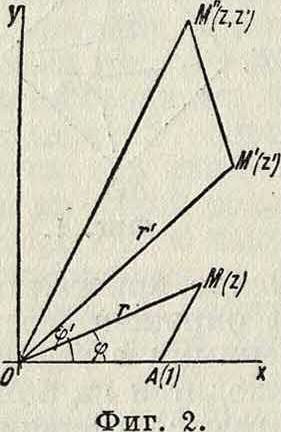
(а + Ьг) - (а + bг)=(а — а)+г(Ь — b). Умножение К. ч. производят по правилу умножения многочленов, принимая во внимание условие г2=— 1. Таким образом ζ ζ= (а + Ы) (a+bi)=aa—bb+i (ab+ab). Если перейти к тригонометрической форме, г=г (cos φ + г sin φ), ζ=r (cos<p -fi sin<p). то формула, умножения даст:
Z Z=rr [COS (φ + φ’) + г sin (φ + φ)), τ. е. при умножении К. ч. модули перемножаются, а аргументы складываются. Геометрии. построение точки М", изображающей произведение zz: на действительной оси (фигура 2) берем точку А, изображающую 1, и на отрезке ОМ строим Δ ОММ”, подобный Δ О AM. Т. о. геометрия, смысл умножения z на z таков: изменяем длину вектора множимого в отношении г (мюдуль множителя) и поворачиваем этот вектор на угол φ (аргумент множителя). Произведение двух сопряженных К. ч. равно действительному числу, квадрату модуля:
(a -(- Ы)-(а—Ы)=а2 + b2=а + Ы 2= а — Ы 2.
При делении К. ч. частное выражают в виде дроби и умножают числитель и знаменатель на число, сопряженное знаменателю, чтобы избавиться от мнимости в знаменателе:
z а + Ы (а +bi)(a- bi) z ~ а + bi ~ (а + bг) (а - bг) аа + bb, · аb - ab
= Va + b8- + 1 ог+ Ьа
Деление невозможно лишь в случае, когда α= &=0 (деление на нуль). В тригонометрической форме имеем:
~=ψ [cos (φ -φ) + ί sin (φ - φ)].
Возведение в степень. Пользуясь тригонометрия. формой К. ч.
z=г (cos φ + г sin φ)
и применяя формулу умножения п раз, получим: Zn=r”(COS ηφ + i Sin ηφ), τ. е. модуль возводится в степень, а аргумент умножается на показатель. Полагая в частности г=1, имеем тождество:
(cos φ + г sin φ)η=COS ηφ -f i sin ηφ (ф-л а М о а в р а). Приравнивая в обеих частях действительную и мнимую части, имеем тригонометрич. тождества:
COS ηφ=cos” φ — (2) COSn—29? sin2 φ -f
-f cos”-4<psin4?> —.
sin ηφ=cos”-1<p sin φ — Q) cos”~^?>sin3¥>-|-
+ Q) cos”~5?> sin5 φ —.
При извлечении корня w-йстепени надо извлечь корень из модуля и разделить аргумент; в виду неоднозначности аргумента получается п различных значений корня. Пусть
Ζ=Г (COS φ + г sin φ), где 0 φ < 2π очевидно, что также
ζ=г [cos (φ + 2π) +i sin (φ -f 2я),.;
тогда yfz дает всего п разных значений; (cosf + isin?);
Цсов.^+tsin^);
Гг [cos * + + г sin.
71 71 J
Если в частности я=1=cos 2кл + г sin 2кл (к=0, ± т0
Щ
о. о *
cos - + г sin -= 1;
п 1 п 7
w. 2π. 2π.
i/l=cos —Ь г sin -,
η η
η/ζ 2(η — ί)π.. 2(η-ΐ)η
1/1=COS — — 4- г sin —-— ·
r η 1 η
Все эти корни расположатся в вершинах правильного w-yголышка, вписанного в круг радиуса 1.
Показательная форма К.ч. Определим значение показательной функции для мнимого показателя помощью ряда Тейлора (смотрите Дифференциальное исчисление):
β ψ=1 4- ”
(ίφ)2 2!
+ М8 +
^ 3! ^
+Sr-.+*C-S+J·
Действительная часть и коэфициент при г в правой части представляют собой разложения cos φ и sin φ. Таким образом
Αφ
e=cos φ -f- г sin φ ; заменяя г на —г, получим:
-гsin φ.
— ΐφ
e=COS φ
(1)
(2)
Из формул (1) и (2) получаем выражения тригонометрических ф-ий через мнимые показательные:
cos φ =
-ίφ
Sin φ =
e^-e
2 ’ Y 2i
(ф-лы Эйлера). Подставляя выражение (1) в К. ч. (в тригонометрич. форме), получаем показательную форму:
г=гег<р (г—модуль, φ—аргумент). Заметим, что из ф-лы (1), в которой принимаем ψ=2кл, на основании тождества: cos 21<л + г sin 2кл=1,
получим:
ваад-1(к-0,±1,±2,.).
Были сделаны многочисленные попытки (Гросман, Гамильтон)построить более сложные комплексные числа т. о., чтобы действия над ними сохраняли законы обычных арифметических операций. Это однако оказалось невозможным. Различные системы так. наз. гиперкомплексных чисел построены, но действия над ними всегда в том или ином отношении отличаются от действий над обыкновенными чи. Наибольшее значение имеют т. наз. кватернионы Гамильтона, приведшие к современной теории векторов (смотрите Векторное исчисление). Кватернионы—гиперкомплексные числа с 4 независимыми единицами: 1, г, j, к. Общий вид кватерниона:
q=d + га + jb + кс
(d, а, Ь, с—действительные числа); в этом выражении d называется скалярной частью и га + jb + кс есть вектор в пространстве. При сложении кватернионов складываются скалярные части и компоненты вектора; умножение распределитель но и сочетательно и определяется законом умножения единиц:
ij—k, jk=i; ki — j; г2=)2=/г2=— 1; ji=— ij; kj=— jk; ik=— ki (умножение не переместительно). lio этому правилу произведение двух векторов дает кватернион, у которого скаляр!-ная часть есть внутреннее (скалярное) произведение векторов с обратным знаком, а вектор—внешнее (векторное) произведение векторов:
(га + jb + ко) (гх 4- jy + kz)=-ax — by — cz- -+ i(bz — су) + j (cx — az) + к (ay — bх).
В тригонометрич. форме кватернион выражается следующим образом:
q=г cos Ώ + ir sin Ό cos a -f jr sin D cos β 4-+ fer sin D cos у=г (cos D + ε sin D),
здесь ε—единичный вектор в направлении оси кватерниона, которая образует углы а, β, у с тремя взаимно перпендикулярными векторами г, j, к; D называется углом кватерниона, г=Vd2 + а2 + й2 + с2 его тензором (нормой). При Г>=^ получается чистый вектор. Кватернионы имеют приложение в механике (твердого тела) вследствие их геометрическ. значения: с их помощью изображается поворот в пространстве около оси кваферниона на угол D[ с одновременным растяжением (сжатием) в отношении г.
Лит.: Ланин Л. К., Энциклопедия элементарной математики, ч. 1, М., 1924; Привалов И. И.!, Введение в теорию функций комплексного переменного, М.—Л., 1927; Н a m i 11 о n W. R., Elements of Quaternions, v. 1—2, L., 1899—1901; Backer, Quaternions, London, 1911. В. Степанов.