 > Техника, страница 54 > Компрессоры
> Техника, страница 54 > Компрессоры
Компрессоры
Компрессоры, машины для сжатия возр духа и других газов и паров до б. или м. вын сокого давления. Строгой границы между К. и воздуходувными машинами (смотрите) провести нельзя; можно сказать, что К. называется воздуходувная машина, сжимающая воздух от 4—5 atm и выше. К. делятся на два больших класса: поршневые компрессоры и турбокомпрессоры. Основным процессом в тех и других является сжатие газа.
Сжатие в К. В основных расчетах К. сжатие. принимают происходящим или без сообщения и отнятия тепла (адиабатически), или при сохранении постоянной р t° (изотермически), или наконец по какой-либо про-межуточ.кривой (п о-л и т р О п а). Так как степень сжатия в одном цилиндре К. не бывает никогда особенно большой, то можно делать расчеты для воздуха и других газов, принимая теплоемкости постоянными и вообще пользуясь законом для идеальных газов. Рассматривая «идеальные» процессы для К. (фигура 1), не принимая во внимание величины вредного пространства, понижения давления при всасывании вследствие имеющих место сопротив-
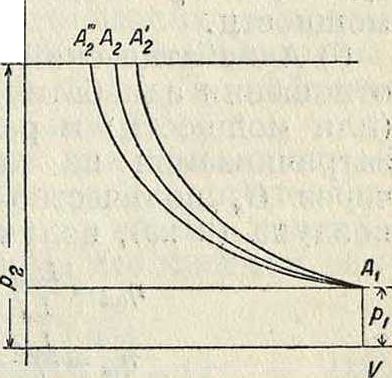
Фигура 1.
лений при всасывании и выпуске, получим следующие формулы. а) Изотермическое сжатие (кривая ΑιΑ4). Работа изотермического сжатия для 1 кз газа:
Ьй-РАInf-;, (!)
где Рх—давление всасывания в килограммах/м2·, ρί— то же в кв/вм2, р2 — давление нагнетания в килограммах/см2, ντ—удельный объём всасываемого газа в м3/кг. б) Адиабатическое сжатие (кривая AjAa)
Ьяй=^Рл[(Й¥-1, (2)
ALad — Ср (ia — ίι), (3)
где А—термич. эквивалент механич. работы, к=св (отношение теплоемкости при постоян-
С®
ном давлении к теплоемкости при постоян-ном объёме), ίχ—начальная температура, V2— конечная темп-pa адиабатического сжатия. в) Политропическое сжатие (кривая А^). Ф-лы те же, что и для адиабатич. сжатия, но только вместо к надо подставить всюду величину показателя т политропы. Наименьшей работы требует изотермическ. сжатие, наибольшей—адиабатическое, как показывает следующая таблица:
| Ра
Pi |
Lad в жм | Lgd
Lis |
Гг~ U |
| 2 | 6 150 | 1,106 | 64° |
| 3 | 11 080 | 1,175 | 108° |
| 4 | 14 590 | 1,227 | 142° |
| 5 | 20 000 | 1,305 | 196° |
| 8 | 24 400 | 1,367 | 238° |
| 10 | 28 000 | 1,416 | 273° |
| 25 | 45 400 | 1,644 | 443° |
| 50 | 61 800 | 1,840 | 603° |
Эта таблица указывает на необходимость заботиться о надлежащем охлаждении цилиндра К. для приближения процесса, происходящего в нем, к изотермическому, т.к. адиабатич. процесс при больших сжатиях дает чрезвычайное превышение работы.
Коэфициенты полезного действия. а) Механический кпд:
т индикаторная работа Ьг· работа, затрачиваемая на К. Le
Ni
Ne’
(4)
где JV,· и Ne—индикаторная и эффективная мощности. б) Адиабатический и изотермический кпд: отношения адиабатич. и изотермич. работы (или мощности) к работе (или мощности), затрачиваемой на компрессор; обозначив через Gs количество засасываемого в ск. воздуха (в килограммах), получим:
*7 = hsA (*s Lad iad Le = 75Ne >
(5)
n=^?S Lis. /is Le = 75iVe
(6)
Обратно, зная один из этих коэф-тов (или задавшись им) и вычислив по вышеприведенным формулам значения Lad или Lis, можно найти Ne.
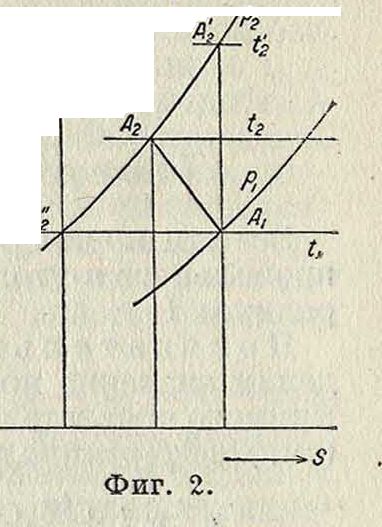
Энтрная диаграмма. На фигуре 2 изображена энтрная диаграмма процесса сжатия в К.: линии сжатия соединяют между собой кривые постоянных давлений рх и р2. Линия АХА2—адиабата, АгА"—изотерма, АгА2—политропа.
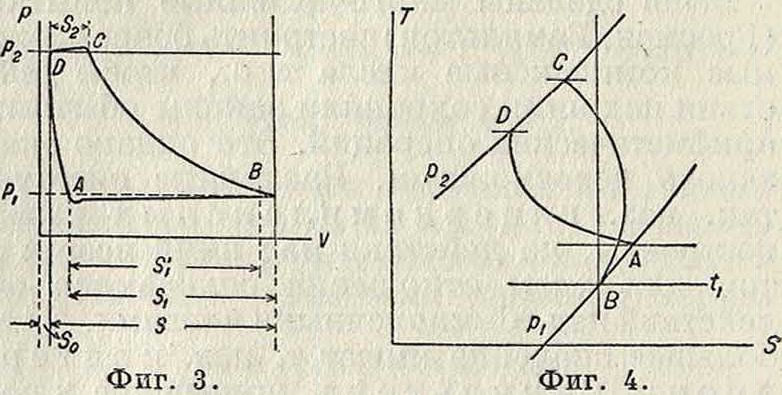
!. Поршневые К. а) Отступления от идеального процесса. В реальных поршневых К. линия всасывания АВ (фигура 3) Тлежит несколько ниже * линии внешнего давле- · ния рх вследствие сопротивлений во всасывающей трубе и во всасывающих клапанах.
Истинное давление всасывания меньше рх примерно на 5 %. По тем же причинам линия выпуска-DC лежит выше линии давления р2 (в среднем на 3—5%). Вследствие обмена тепла между сжимаемым воздухом и стенками цилиндра линии сжатия ВС и расширения DA отступают от политроп. Примерный вид линий расширения и сжатия дан на фигуре 4, изображающей энтрную диаграмму реальных процессов сжатия и расширения. Как показывает линия ВС, сначала сжатие сопровождается отдачей тепла стенками, а затем обратно — стенки начинают поглощать теплоту. В линии расширения ΏΑ сначала происходит отдача тепла стенкам, а затем обратно—сильное нагревание расширяющегося газа. При применении политропы для расчета работы К. следует полагать: для политропы расширения т=1-У1,2, для политропы сжатия m=1,4. Объемный кпд и к о э ф и-циент наполнения К. Вредное пространство, понижение давления всасывания, нагревание воздуха во время всасывания и неплотности поршня и клапанов вызывают уменьшение количества действительно всасываемого воздуха против теоретического (равного полному объёму цилиндра). Отношение приведенного объёма действительно засасываемого воздуха к теоретически возможному называется коэфициентом наполнения К. и обозначается через λ. Если обозначим вес засосанного за один ход воздуха
через Gn, а его уд. объём (определяемый по давлению и ί° во всасывающей трубе) — νη, то получим действительно засосанный объём V^Gnvn. (7)
Рабочий объём цилиндра Vh=FS (где F— площадь поперечного сечения цилиндра, а
S—ход поршня); для коэф-та наполнения λ получим выражение:
(8)
Главное влияние на уменьшение засасывав-
мого количества воздуха имеет расширение сжатого воздуха, находящегося во вредном пространстве. Вследствие этого расширения путь всасывания (фигура 3) меньше хода поршня S. Назвав отношение объёма вредного пространства к рабочему объёму Vh цилиндра через σ0 и приняв линию расширения за политропу с показателем то, получим для отношения=А0, объёмн. коэфициента полезного действия К., выражение:
| (9) | |
| положить | |
| λ=αλ0, | (Ю) |
причем а выбирается между 0,9 и 0,95. Величина коэфициента наполнения А выбирается для К. до 7 atm конечн. давления между 0,86 и 0,92; для доменных воздуходувок—· между 0,82 и 0,90; для небольших К.—0,70 и выше. Если задаться данными: <г0=0,05,
«1=1, то формула (9) дает при ^= 21, До=0.
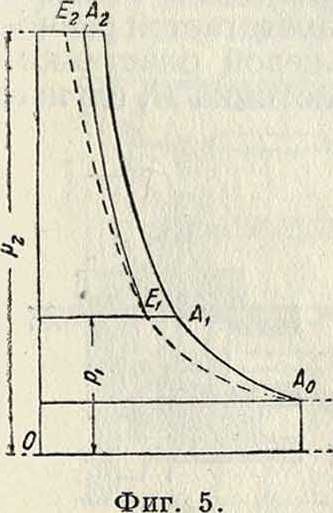
Отсюда ясна необходимость применения многоступенчатых К. при высоких сжатиях. Сжатие в нескольких цилиндрах с промежуточным охлаждением необходимо также в виду чрезмерного повышения 1° во время сжатия, причем может произойти имеющейся в цилиндре смеси смазочного масла с воздухом. б) Многоступенчатые К. Теоретич. индикаторная диаграмма двухступенчатого К. изображена на фигуре 5. Энтрная диаграмма трехступенчатого К. представлена на фигуре 6. При этом принимается, что охлаждение в промежуточном охладителе (линия А1Е1 на фигуре 5) доводит t° сжатого газа
| 7 | У | У | |
| /1, | |||
| As Аз | А | ||
Фигура 6.
до t° в начальной точке А0 сжатия (фигура 5). Далее исходят из предположения, что конечные t° конца сжатия во всех цилиндрах тоже равны между собой (точки Аг, А4, А6 на фигуре 6). Эти предположения приводят к равенству отношений давлений:
(Н)
откуда
Pj — Pj — Р‘ _ т Р. Р« Рг ’
-Г!·
(12)
Вообще при г ступенях принимают отношение давлений в одной ступени
-(у)
(13)
При больших давлениях сжатия (в 50 atm и выше) указанные элементарные приемы вычислений дают неточные результаты вследствие переменности величин теплоемкостей. Лучше всего пользоваться в этих случаях эн трными диаграммами для воздуха [“,2]. Введение большого числа ступеней имеет и свои отрицательные стороны, т. к. при этом усложняется и удорожается конструкция и получаются потери давления при переходе из одного цилиндра в другой. Поэтому К. обыкновенно не выполняют больше 3 ступеней и только при очень высоких давлениях (2U0 atm) применяют пятиступенчатый К.
в) Определение главных размеров К. При заданном (или вычисленном) секундном объёме Vn засасываемого воздуха (в л13/ск) получим основное ур-ие для расчета размеров одноступенчатого К.:
(14)
ТГ. FSn,
1» ~ 1 ЯП ^ >
где j—число работающих сторон в цилиндре К. (2—для К. двойного действия, 1·—для К. простого действия), F—полезная площадь поршня (в Л12), S—ход поршня (в ж), п— число об/м., А—коэф-т наполнения. В этой формуле кроме Vn при проектировании являются известными величины j и и; коэфициен-том А задаются, как было указано выше. Неизвестными величинами являются F и S. Ход поршня связан с числом оборотов п и средней скоростью ст поршня ф-лой:
«»~!г· <15),
Средняя скорость ст поршня выбирается в пределах от 2 до 4 м[ск. Найдя S, можно определить площадь поршня F по формуле (14), а затем и диаметр поршня из соотношения:
~=F (16)
(на площадь поперечного сечения штока прибавляется 2—3%); при этом отношение ^
выбирают ^ 2. Площадь сечения всасыва-π Г)2
ющей трубы - выбирается по фиктивной средней скорости воздуха гггиз соотношения:
πβ2 πβ2
4--Cm= (17)
W; берется от 15 до 20 м[ск. Диаметр нагнетательной трубы определяется по аналогичной ф-ле; скорость воздуха в нагнетательной трубе берется равной 20—30 м/ск. В многоступенчатых К. объём цилиндра низкого давления определяется тоже по формуле(14). Объемы цилиндров для последующих ступеней определяются по отношению удельных объёмов газа, поступающего в эти цилиндры. Эти удельные объёмы м. б. удобно найдены из энтропических диаграмм С1,2].
Мощность, требуемую для приведения в движение одноступенчатого К., определяют по среднему индикаторному давлению р(. Для нахождения его имеются сле-
| формулы: | |
| Ш 1 | (18) |
| γ. _Pith | (19) |
| λτ F Pi cm ~ 75 ’ | (20) |
где рт—теоретическ. среднее индикаторное давление и т—показатель политропы, который можно принять равным 1,4; %— коэф., выражающий влияние потерь на торможение и т. in., его можно принять равным в среднем 0,94. Индикаторная мощность для многоступенчатых К. определяется суммированием мощностей, получаемых для отдельных ступеней. Обозначив через AL„d теоретич.
Фигура 7а. Фигура 76.
мощность, затрачиваемую при сжатии по адиабате в одной ступени 1 килограмм газа в 1 ск., получим полную индикаторную мощность для всего К. при производительности Gs кг в ск. (учитывая еще потери на неплотности):
Л,-(1,03 4-1,06)0.2^· (21)
Необходимая эффективная мощность Ne определяется по выражению:
Ne=^; (22)
г‘т г]т берется при паровом двигателе 0,85— 0,95, при электромоторе или ременной пере-
Фигура 8. Фигура 9.
даче 0,79—0,83. Зная Ne и Nis, можно найти величину коэфициента величина его для К. с паровкм двигателем, отнесенная к эффективной мощности последнего, принимает обыкновенно численные значения 0,72— 0,78, отнесенная же к индикаторной мощности
парового двигателя—0,65—0,74. Расход тепла на сжатие 1 м3 до 7 atm равен при обыкновенных паровых машинах 450 Са], при га зовых двигателях—250 Cal. Расчеты прочих деталей поршневых К. производят так же, как для паровых машин. г) Детали и,типы поршневых“К. Важнейшей деталью К. являются распределительные органы. Чаще всего применяются
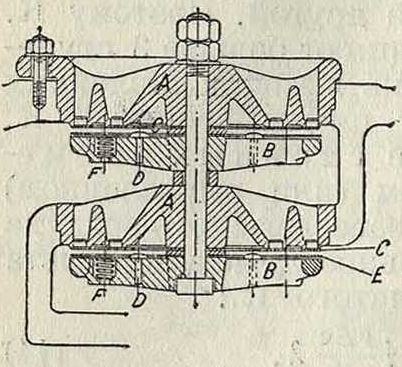
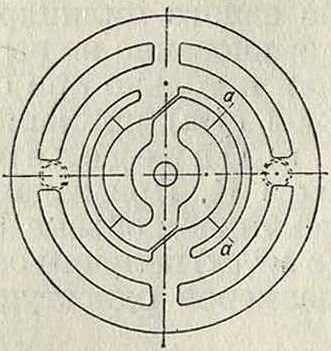
пружинные клапаны с малой массой и небольшим подъемом (3—4 м) для уменьшения, ударов. На фигуре 7а и 76 изображены клапаны Гербигера завода MAN (Аугсбург-Нюрнберг). Между седлом клапана А и упором В (фигура 7а) лежит стальная пластинка С толщиною 2 миллиметров, зажатая в середине. Дуговые части а, а пластинки С, изображенной в плане на фигуре 76, для большей эластичности сошлифо-ваны до 1 миллиметров толщины. При подъеме внешних кольцевых пластин тонко отшлифованные части пластин С упираются в головки медных заклепок Ό, чем и достигается равномерный прогиб всей кольцевой пластинки. Перед упором В лежит пластинка Е, служа
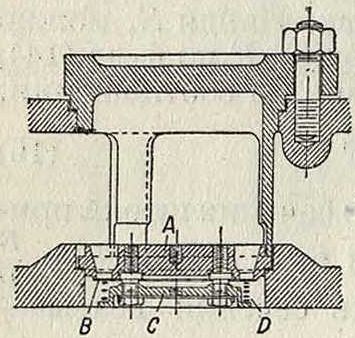
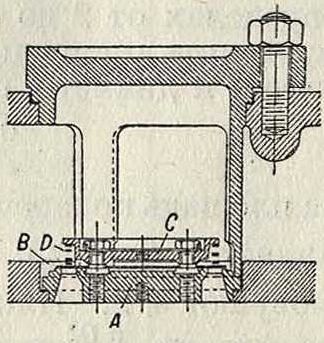
щая буфером для смягчения ударов и для i уменьшения шума, происходящего при работе клапана; для той же цели служат две-; спиральные пружины F. На фигуре 8 и 9 изображены применяемые для всасывания и нагнетания пластинчатые клапаны завода ; Борзига. Перекрывание клапанного седла А производится кольцеобразной стальной пластиной В толщиной от 3/4 ДО 2 миллиметров. Между упором С и пластиной В помещена пружина D. Клапаны Гутермута представляют собой тонкую стальную пластинку (толщиною от 1 до 1,5 миллиметров), наворачивающуюся одним концом на неподвижные штифты. Пластинка эта является одновременно клапаном и пружиной. Применение клапанов Гутермута в-
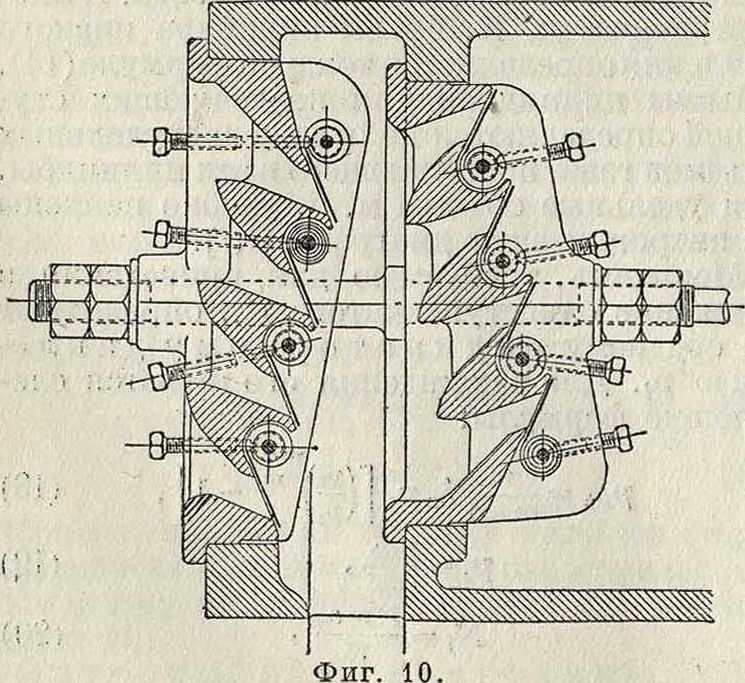
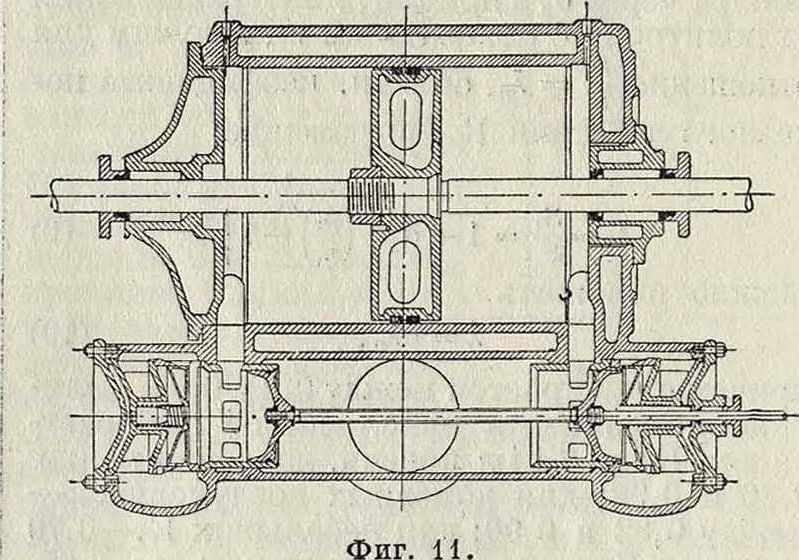
воздуходувной машине показано на фигуре 10. Золотники, применяемые иногда в К., управляют только впуском; для выпуска сжатого воздуха в этих золотниках ставят клапаны, управляемые пружинами, чтобы выпуск происходил всегда при определенной величине сжатия. Пример такой конструкции (золотник Кестера) изображен на фигуре 11.
Регулирование К. устраивается различно, смотря по тому, от какого двигателя приводится в движение К.; К., соединенные с паровыми машинами и газовыми двигателями, регулируются путем изменения числа оборотов, а К., приводимые в движение помощью электромоторов или ременной передачи,—другими способами. В этих последних К. имеются специальные приспособления для изменения ко-лич. подаваемого возду-ixa без изменения числа }оборотов. Изменение числа оборотов м. б. достигаемо путем ручного регулирования машины двигателя (торможением пара или изменением степени наполнения), путем ручного ate воздействия на центробежный регулятор с изменением его нормального числа оборотов, путем подкручивания пружин, действующих на муфту регулятора, так называемым регулятор подачи (Leistungsregler),
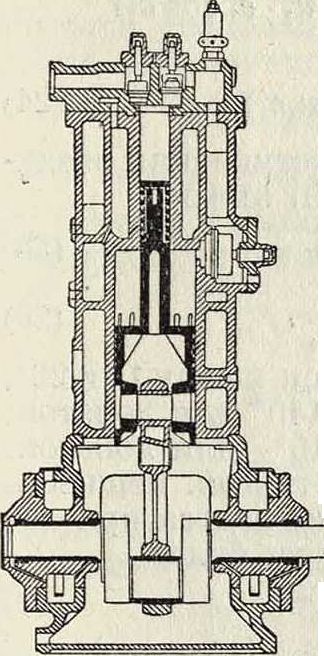
Фигура 13.
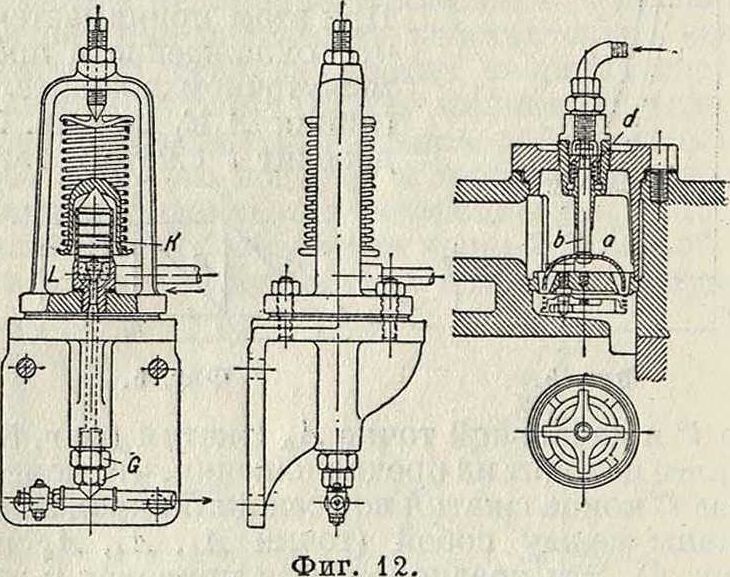
тие всасывающих клапанов, что дает возможность всосанному воздуху вновь уйти из цилиндра К. Конструкция з-даБорзига для этой цели изображена на фигуре 12. Поршенек К. с вентилем L находится под действием сжатого воздуха в воздухопроводе. При нормальном давлении вентиль L закрыт под действием
Фигура 14.
пружины, но при повышении давления он открывается, и сжатый воздух проникнет в трубу G и по ней к поршеньку d, соединенному с захватом аb, к-рый опускается, отжимает пластинку всасывающего клапана и держит клапан открытым во время сжатия.
Типы поршневых К. Небольшие К. конструируют б. ч. с электромоторами или с приводом от ременной передачи. В случае сжатия в двух ступенях применяется обык~
наконец путем автоматич. воздействия давления в нагнетательной трубе К. на парораспределение машины. При регулировании на неизменяемое число оборотов К. нормально работает на наибольшее колич. подаваемого воздуха. Регулирование должно уменьшать подачу при уменьшении расходавоздуха. Способы такого регулирования различны. Одним из способов является например автоматич. по дня-
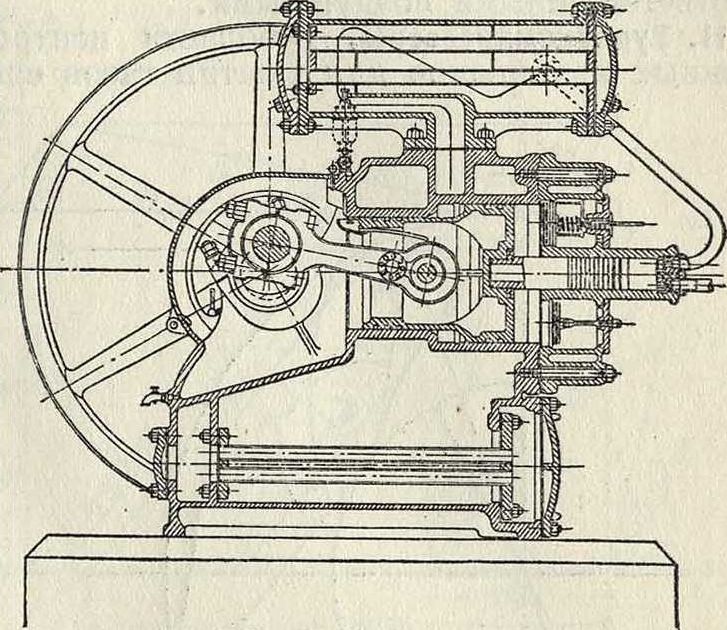
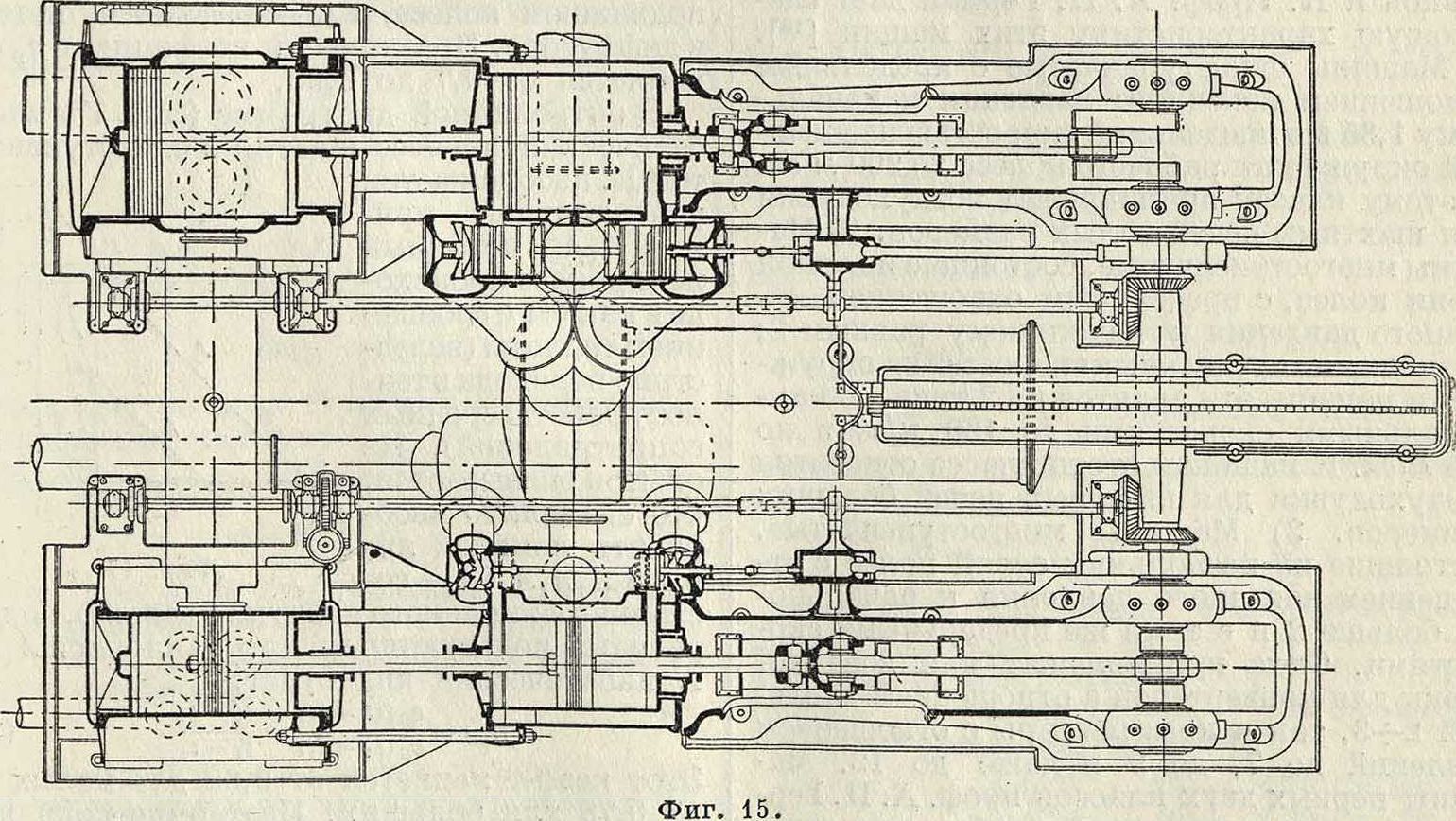
новенно одноцилиндровая конструкция со-ступенчатым поршнем. На фигуре 13.изображен. такой К. завода Балыда вертикального типа. Охлаждение достигается в нем отчасти водяной рубашкой, отчасти воздушным слоем вокруг цилиндра. Трехступенчатый горизонт. К. с водяным охлаждением и ступенчатыми поршнями з-даГартман изображен нафигура14. Большие К. делаются со сжатием в отдельных. цилиндрах и приводятся в действие от паровых или газовых двигателей. Конструкция парового двухступенчатого К. завода Покорный и Витекинд изображена на фигуре 15. Распределение осуществляется золотниками системы Кестера. Паровая машина—компаунд, паровые цилиндры расположены за соответственными воздушными.
II. Турбокомпрессоры. В области центро-безкных механизмов для сжатия газов еще
труднее провести границу между воздуходувкой и К. Проф. А. П. Герман дает следующую характеристику этих машин [13].
1) Машины одноступенчатые с предельным отношением конечного давления к начальному 1,35 и с предельной скоростью на внешней окружности рабочего колеса до 200 м[ск. К этому классу принадлежат воздуходувки для шахтных печей малых размеров. 2) Машины многоступенчатые, состоящие из одной серии колес, с предельным отношением конечного давления к начальному равным 2; в отношении предельных скоростей на окружности машины эти делятся на 2 типа—с максимальными скоростями до 130 м/ек и до 200 м/ск. К машинам этого класса относятся воздуходувки для шахтных печей больших размеров. 3) Машины многоступенчатые, состоящие из нескольких серий колес с отношением конечного давления к начальному больше 2 и с теми же предельными скоростями. Сюда принадлежат как воздуходувки для конвертеров с отношением давлений 2-1-3, так и компрессоры с отношением давлений до 7, до 9 и даже до 12. Машины первых двух классов проф. А. П. Герман предлагает называть турбовоздуходувками, машины третьего класса — турбокомпрессорами.
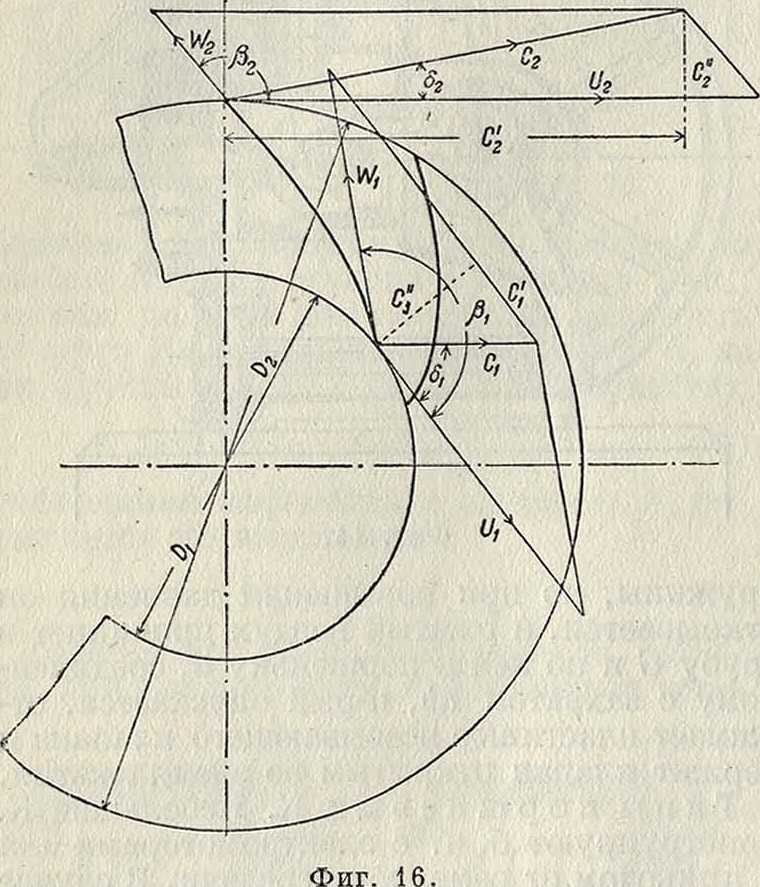
Одноступенчатый турбокомпрессор (без охлаждения). Основы теории—те же, что и для центробежных вентиляторов (основные ур-ия сходны также с основными ур-иями центробежных насосов). Принимая обозначения, показанные на фигуре 16, получим для теоретич. напора, выражен ного в м воздушного столба, выражения:
Н=-
Ь + -
(23)
2 д 2 д 1 2 д где щ и иг — соответствующие окружные скорости колеса, г^и гс2—относительные скорости струи при входе и при выходе из колеса, ел и с3—соответствующие абсолютные скорости. Заменив величины wx и w2 величинами щ, и2, сг и с2, получим:
Н=~ (щ · е2 cos <5г — % · C1 cos (5J
или
Л=(м2С2 — UjC[). (24)
Для случая нормального вступления воздуха в колесо (<5j=90°; с(=0) имеем:
?l-i
НИ
= Ψ 1-tg
(25)
(26)
tg βί — tg ό2
Значение угла <52 колеблется между 14 и 28°, а угла β2 —между 120 и 140° для лопаток, загнутых назад, и около 45°—для лопаток, загнутых вперед [7]. Теоретическ. мощность для приведения в движение насоса при подаче G кг воздуха в минуту будет
Гидравлическим кпд наз. отношение действительно получаемой высоты напора к теоретической. Остертаг L1] дает для нег0 выражение:
(!ι Н- la) sin β2 i
ηρ ~ 1 [г
+ί
(28)
L2 sin (/32 -tf2) cos г2
l.sin(/S, — <S2)_t ~
2 sin/S2 C0S<52 4 1
в котором ξ1—коэфициент потери энергии в подвижном колесе, a f2—коэфициент потери в диффузоре. Практически коэфициент ηρизменяется от 0,7 до 0,88.
В энтрной диаграмме (фигура 17) адиабатический процесс сжатия в одноступенчатом К. изображается вертикальной прямой A-lAz, истинный же процесс происходит как бы с сообщением теплоты (вследствие перехода в теплоту работы вредных сопротивлений). Из опытов оказывается, что его можно изобразить ломаной линией AjA^A^Ag—состояние сжимаемого воздуха в зазоре), но для расчетов пользуются просто наклоннойИ^. Адиабатический кпд будет:
^_; Ср(ia — ti) ^ 12 — ίι
6ρ(ί2 — ί l) ί2 — ίΐ
| &г | |||
| у | V | L | |
| У ^ | К | ||
| 1/р, | |||
| /1 | А, | 1 | |
Фигура 17.
Vad =
(29)
Этот коэф-т меняется от 0,66 для малых К. до 0,78 для больших. Изотермический кпд при давлениях сжатия 6—8 килограмм/см3 по манометру изменяется от=0,86 при V==4 000 м3/ч до 0,70 при 80 000 м3/ч. Эффективная мощность Ne при секундном расходе газа=9 килограмм определяется по ф-ле:
^ AL_427G_ (30)
е 75<!ОТ v ’
Пользуясь энтрн. диаграммой, получим: А1*-ср&-Ь). (31)
Механический кпд η„, изменяется в пределах от 0,95 до 0,98.
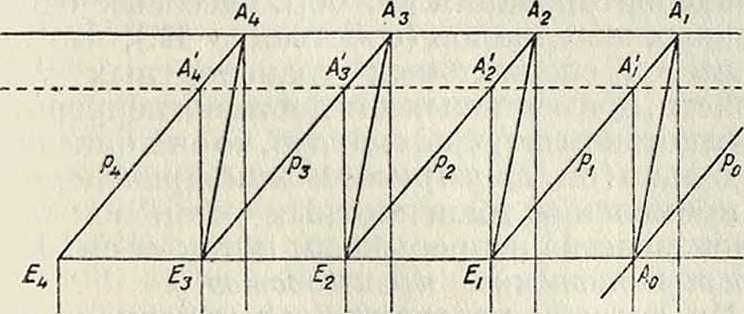
Многоступенчатые турбокомпрессоры без охлаждения. В этих К. часто охлаждение делается только впро-межуточн. охладителях между двумя сериями колес, т. к. охлаждение в каждой ступени усложнило бы конструкцию. При небольшом сжатии все расширение получается в 2—3 ступенях в 1 кожухе и без охлаждения. Энтрная диаграмма такого компрессора изображена на фигуре 18. В каждом колесе получается полезная высота
, «* и“
й== «.
(32)
Я "2 д где т=2ψηρ. Обозначив через гц, «;,„2и г>„!зуд. объёмы в различных ступенях, получим следующие ур-ия для определения давлений:, h
Pi=V о + :
Рг=Vx + Рз=Pi +
Vm1
h
V™2
h
(33)
Работа на окружности колес получится из уравнения:
AL—Cp^ty—10) -j-<?p(f2— fi) +
+ cp(t3-t2)=cp{ta-10). (34)
Многоступенчатые турбокомпрессоры с охлаждением в отдельных ступенях. При полном охлаждении воздух должен в конце процесса сжатия и перепуска в диффузор принимать начальн. температуру. За энтрную диаграмму можно принять зигзагообразную линию A^E^E.^E-jAiEf (фигура 18). Обыкновенно отношения давлений конечного к
Фигура 18.
начальному во всех ступенях принимаются одинаковыми, поэтому
Ρι=яр“, Рг=χΡι=χ2Ρο, · · ·; Ρζ=χΖΡο, (35)
—Ο4· <*»
Работа при этом предположении распределится равномерно между ступенями; полная работа на ободе определится из следующего выражения:
АЬ-еер(Тг-Т^. (37)
Вся эта работа переходит в теплоту, которая должен быть отнимаема в охладителе, кроме последней ступени (в которой воздух обыкновенно не охлаждается). Поэтому количество отнимаемой теплоты будет д=(2-1)е„(Т1-Т0). (38)
Повышение давления в первой ступени равно h=(Pl - Vo) Vm^=-1) Vovmι μ возд. ct. (39)
При наших предположениях во всех ступе нях будет одинаковое повышение давления. При неполном охлаждении конечная точка первой ступени не совпадает с начальной, как это видно из следующего примера t1].
Пример. Рассчитать трехступенч. турбокомпрессор для повыш. давл. на 1,2кг/см2 при расходе 0=465 килограмм/мип. Прибавляя 6%
вое“
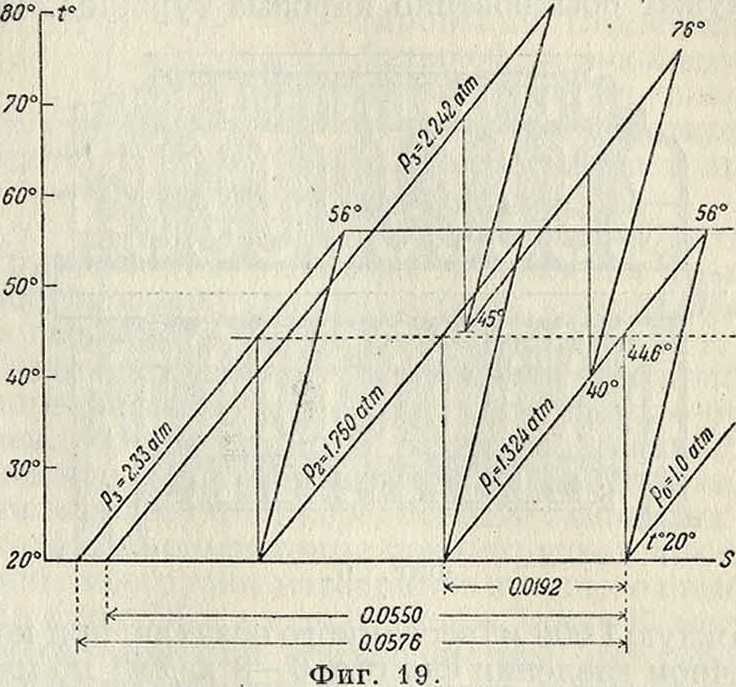
на потери в воздухопроводе, получим конечное давление равным 2,2+0,06-2,2==2,33 килограмма/см2. Гидравлический кпд ηρ можно положить равным 0,77, коэфициент <р=0,83, адиабатический кпд ??ад.=0,68. Энтрные диаграммы процесса для полного и неполного охлаждения изображены на фигуре 19. По нашим ф-лам найдем для случая полного охлаждения:
х=1/2733=1,324;
р0=10 000 килограмм/л2; р1=13 240 килограмм/л2; φ1 — р0== 3 240 килограмм/м2;
р2=1,750 килограмм/см2; р3=2,33 килограмма/см2; v„h=0,8 л8/кг; h=(р, — р0)=3 240
= 2592 метров возд. ст.
Из ур-ия h=φηρ — найдем:
0,8 =
9,81 · 2 592
£=200 м/ск:
0,83 · 0,77
AL=(44,6 - 20)=25,9 Са1/кг. механическом
Эффективная мощность при кпд р)К=0,97 будет равна
465-60-25,9
= 1180 №.
632 - 0,97
Неполное охлаждение: после 1-й ступени воздух охлаждается до 40°, после 2-й—до 45°. Высота h остается прежней. Из энтрной диаграммы можно найти величину работы в отдельных ступенях:
AL =0,24(56 —20)= 8,60 Cal/кг AL" =0,24(76 -40)= 8,60 Cal/кг
AL"=0,24(80,6 — 45)=8,52 Са1/кг
/+=25,72 Са1/кг
Конструкция многоступенчатых турбокомпрессоров. Пример конструкции такого К. с водяным охлаждением дан на фигуре 20 (смотрите Воздуходувные машины). Такие К. предназначаются для по-
25
Т. Э. m. X.
дачи больших количеств воздуха. Связь между подаваемым в секунду объёмом Vn и числом п об/м. определяется по ф-ле:
Vn>22,^ м3/ск,
при п=3 000, FB>2,45 ms/cks;9 000 м3/ч. При F„=10 000 м3/ч берут «=4 500. Двигателями для крупных турбокомпрессоров служат обыкновенно паровые турбины. На
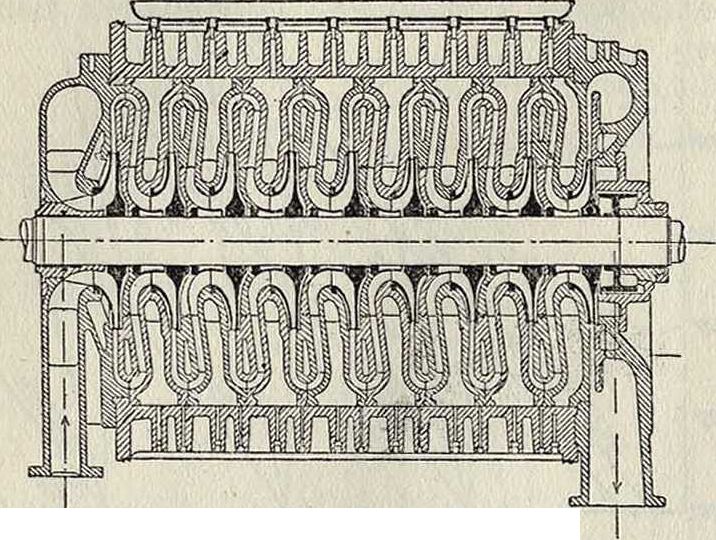
Фпг. 20.
каждую 1 000 м3 всосанного воздуха, при конечном давлении сжатия 6—8 килограмм/см2 по манометру, расход пара достигает от 600 до 850 килограмм при турбинах, работающих на свежем паре, и от 1 200 до 1 400 килограмм при турбинах, работающих на отходящем паре. Детали конструкций турбокомпрессоров и их расчет сходны с деталями и их расчетом для паровых турбин.
Характеристика турбокомпрессора. Характеристикой турбокомпрессора называется кривая, выражающая зависимость между подачей воздуха в К. и давлением сжатия при постоянном числе оборотов. Опыты показывают, что кривая эта имеет вид, изображенный на фигуре 21,—линия DC КАЕВ. Линия эта состоит из двух частей: поднимающейся ΏΚ и опускающейся КАВ. Точка D на оси ординат соответствует состоянию турбокомпрессора с закрытым вентилем в выходящей трубе. Нормальная работа должна происходить близко от точки К нормального рабочего давления К., соответствующего также наибольшему кпд. Притом для устойчивости р ежима К. работа должна происходить на понижающейся части характеристики (примерно в точке А); работа лее на части DK неустойчива и после перехода через точку К подача может сразу упасть до нуля. При увеличении числа оборотов получается более высокая характеристика: DCKA, при понижении—более низкая: D"C"K"A".
Регулирование турбокомпрессоров, как и поршневыхΊί., может преследовать одну из двух целей: 1) поддержание постоян. давления при переменной величине подачи; 2) поддержание постоянной величины подачи при переменном давлении. При этом, в зависимости от рода машины двига
| » в·
У г Г У |
=5
Х>ч |
|
| 1 1 1 | ||
| 1 | ||
| 1
1 1 .i_ |
С
Lb |
йг Va И Фигура 21.
теля, приводящего в движение турбокомпрессор, регулирование может производиться с сохранением числа оборотов (при электромоторах) или с изменением числа оборотов (при паровых турбинах). Регулирование бывает ручное и автоматическое.
Лит.: POstertag Р., Kolben- и. Turbokom-pressoren. 3 Auflage, В., 1923; 2) Н i n z Ad., Thermo-dynamische Grundlagen d. Kolben- u. Turbokompres-soren, 2 Auflage, B. 1927; 3) В a e г S., Dampfturbi-nen u. Turbokompressoren, Leipzig, 1924;*) Regeln fiir Leistungsversuche an Yentilatoren und Kompressoren, 2 Aufl., DIN A4, Berlin, 1926; 5) G r u s s а г d, Venti-lateurs et compresseurs, P., 1926; ·) Kearton W. Turbo-Blowers a. Compressors, London, 1926; ’) G r ο n- v а 1 d E., Zentrifugal-Ventilatoren, B., 1925;8) D u b-b e 1 H„ Taschenbuch fiir Maschinenbau, 4 Auflage, Berlin, 1924 (в русском перев.: Д у б 5 е л ь Г., Справочная книга по машиностроению, т. 1, М., 1929); ·) Н ii 11 e, 25 Aufl., В. 2, В., 1926; “) Бурдаков А. А., Поршневые компрессоры, М., 1928; “) Г е р-м а и А. П., Компрессоры и воздуходувки (лнтогр.), Ленинград, 1924;12) его же, Турбомашины, Л.,1925; в) его же, Теория и расчет турбовоздуходувных машин, Л., 1928. А. Радциг.