> Техника, страница 54 > Коническая поверхность
Коническая поверхность
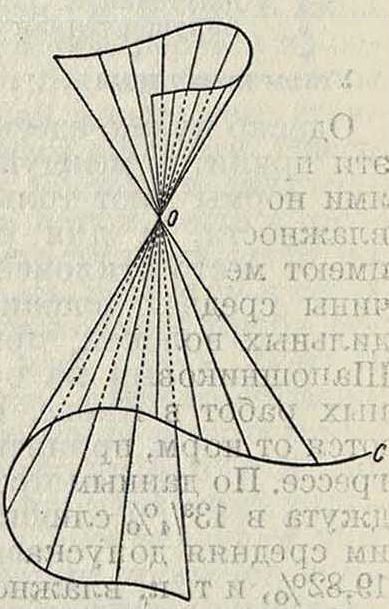
Коническая поверхность, конус, геометрич. место прямых (образующих), проходящих через данную точку (вершину О) и пересекающих данную кривую С (направляющую). Образующие К. п.—; неограниченные прямые, простирающиеся в обе стороны от вершины, почему К. п. составляется из двух полостей, сходящихся при вершине в одну точку (смотрите фигура). Уравнение К. п. всегда однородно; вид его:
Ψ
где х0, у0, 20 — координаты вершины О, а φ—символ произвольной функции. Диферен-циальное ур-ие К. п. таково:
dz
дх
c)z
(р-Хл) + щ{У-Уo)=z - zo
Если при сечении К. п. плоскостью получается алгебраическая кривая η-го порядка, то и поверхность называется алгебраической и-го порядка.
Особенное значение имеет К. п. 2-го порядка; простейший вид ее—п р я м о и круговой конус. Одну полость кругового конуса можно получить путем вращения прямоугольного тр-ка вокруг одного из катетов (о с ь, или в η-ο о т а, конуса). В этом случае гипотенуза является образующей конуса, а направляющая его есть круг, описываемый концом второго катета; площадь этого круга служит основанием конуса. Если высота прямого кругового конуса равна h, образующая равна I и радиус основания равен г, то боковая поверхность его равна лг1, полная поверхность— лг(1+г) и объём—. Поверхность такого
конуса, будучи развернута на плоскость, обращается в сектор радиуса I (образующей) с центральным углом (в градусах) =
Сечения конуса плоскостями дают конические сечения (смотрите)· в Коновалова.