> Техника, страница 54 > Конические сечения

Конические сечения

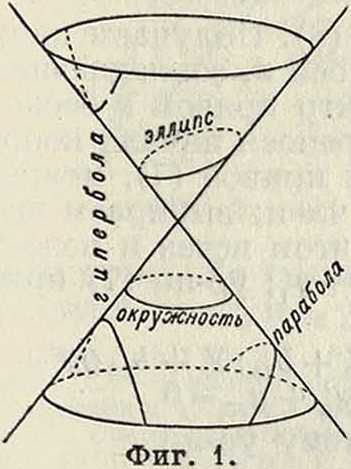
Конические сечения, плоские сечения поверхности прямого кругового конуса (смотрите Коническая поверхность), состоящего из двух бесконечных полостей (фигура 1). Если плоскость сечения не параллельна ни одной из образующих конуса, она пересекает одну полость конуса и дает в сечении э л л и п с— овальную кривую, расположенную целиком в конечн. части конуса; в частном случае, если плоскость сечения перпендикулярна к оси конуса, получается о к-ружность. Плоскость сечения, параллельная одной из образующих конуса, пересекает одну полость конуса; полученная в сечении кривая—п ара-бол а—состоит из одной ветви, распространяющейся в бесконечность. Наконец, если плоскость сечения параллельна двум образующим конуса, она пересечет обе полости конуса; полученная кривая—г ипербо-л а—состоит из двух бесконечных ветвей.

К. с. суть плоские кривые 2-го порядка, то есть они выражаются ур-ием 2-й степени между координатами х я у; я обратно—всякая нераспадающаяся на прямые действительная кривая 2-го порядка есть коническое сечение.

Общее уравнение кривой 2-го порядка имеет след, вид:

а_иж²+2а₁₂а:г/+а₂₂г/²+2а₁зЖ+2а₂₃г/+а₃з=0, (1) где a_itc—действительные числа, не все равные нулю. Разделив ур-ие на отличный от нуля коэф-т, получим в этом ур-ии пять отношений, которые можем определить, давая х и у 5 пар произвольных значений. Т. о. кривая 2-го порядка вообще определяется пятью точками, через которые она проходит. Если заданы дополнительно какие-нибудь специальные свойства К. с., то число определяющих его точек уменьшается. Так например окружность определяется тремя,парабола—четырьмя точками. Кривая (1) носит название кривой 2-го порядка, потому что со всякой прямой она пересекается в двух точках. В самом деле, ур-ие (1) квадратное и имеет со всяким ур-ием 1-й степени у=кх+b два общих решения—корни следующего ур-ия:

(а_п + 2 а₁₂к 4- a₂₂k^z)x² + 2[(а₁₂ + а₂₂к)b +

+ («is + «₂₃ВД* + »22&² + 2а₂₃Ь + а₃₃=0, (2) получающегося заменой у в (1) через кх+ b. Эти точки пересечения м. б. действительные и различные, мнимые и действительные сливающиеся. Левая часть (1) может распадаться на два линейных по ж и у множителя. Приравнивая нулю в отдельности обамножителя, получаем пару прямых. В этом случае кривая (1) распадается на пару прямых, действительных или мнимых, в зависимости от коэфициентов линейных множителей. Усло

вием, необходимым и достаточным для распадения кривой, является равенство нулю дисх^риминанта уравнения (1), то есть детерминанта Ώ:

D =

«11«12«13

«12«22«23

Если кривая (1) имеет бесконечно удаленную точку, то при пересечении ее с некоторой прямой должны получиться точки с бесконечными координатами, то есть при пек-ром значении к получаются бесконечные решения ур-ия (2). Ур-ие (2) имеет бесконечные решения, если коэф-т при ж² равен нулю, то есть «n+2«₁₂fc + a₂₂fc²=0. Отсюда находим значения для к. Т. о. всякая кривая (1) имеет бесхгонечно удаленные точки.

1) Если «ц«₂₂ — «12 < 0, кривая имеет две действительных бесконечно удаленных точки и будет гиперболой, если Ώφ 0; если 11=0, это—пара действительных пересекающихся прямых.

2) Если «ц«2₂ * «12 > 0, кривая имеет две мнимых бесх-сонечно удаленных точки; при 1>Ф 0 это—эллипс; при В= 0—пара мнимых прямых, которые пересекаются в действительной точке.

3) Если «п«₂₂—«12=0, кривая имеет одну (две слившихся) бесконечно удаленную точку; при Ώφ0это—парабола;приD=0—пара параллельных или совпадающих действительных прямых. Выражение

«ц«22 «12 —

«11«12 I _ J

«12«2И !

называется дискриминантом стар-хпих членов ур-ия (1).

Центр кривой. При переносе начала координат в точку (ж₀, у„), то есть при замене *=Х+*<» у=У+У₀ из ур-ия (1) получаем:

«n-X²+ 2«₁₂XY + «₂₂Υ²+ 2(«_иж₀+ а,₂у₀ + «₁₃)Х+ + 2(«₁₂ж₀ + а₂₂у₀ + α₂₃)Υ + Ь₃₃=О, где

^зз⁼«11^ж§“Ь 2«₁₂ж₀2/о+ «22?/о+ 2«₁₃ж₀-|- 2 а₂₃у₀ + «₃₃.

При этом коэф-ты при старших членах пе изменились. Можно выбрать новое начало координат (ж„, у₀) так, чтобы обратились в нуль коэф-ты при×и У. Для этого достаточно решить систему ур-ий:

«11*0 + «12./0 + «13=0 «12*0 + «22?/о + «23=0

(3)

Эта система (3) при условии А Ф 0 имеет единственное решение:

*0--J, У о — 2---

Точка (ж₀, у₀) называется центром кривой, так как оказывается, что всякая хорда делится в этой точке пополам. Хорды, проходящие через центр кривой,называются диаметрами. Кривые типа 1-го и 2-го (Δ ф 0) суть центральны екривые 2-го порядка. В случае их распадения на пару прямых центром Является точка пересечения этих прямых. Для кривых типа 3-го (А =0) система (3) имеет бесконечное или неопределенное решение, то есть либо их центр лежит в бесконечности (парабола) либо имеем бесчислен, множество центров (геометрии, место точек, равноудаленных от двух параллельных прямых,в частности совпадающих).

Главные оси. Уравнение центральных кривых имеет следующий вид:

а_пХ² + 2α₁₂ΧΥ + α₂₂Υ² + Ь₃₃=0. (4)

При повороте осей координат на угол а, то есть при замене

X=х cos а — у sina, Y=ж sin а + ? cos а получаем:

(a_u cos² a + 2a₁₂ sin a cos a + a₂₂ sin² а) ж² + + 2 [(a₂₂ — a_u) sin a cos a + a₁₂ (cos² a —

— sin² a)] xy + (flu sin² a —

— 2ai₂ sin a cos a + a₂₂ cos² a) y² -f- b₃₃=0. (5) Выбирая a так, чтобы коэф. при ж у равнялся нулю, то есть можно привести ур-ие (4) к виду:

bц X² + &22 У² + Ь₃3=0. (6)

кроме случая «_и=«₂₂ и а₁₂=0, когда tg 2a, а следовательно и а неопределенны; но в этом случае само ур-ие (4) имеет вид:

а_и(У² + У²) + 6₃з=0.

Последнее есть ур-ие круга. Итак всегда существуют перпендикулярные направления осей координат, при которых ур-ие центральных кривых имеет вид (6); эти направления называются главными; диаметры, лежащие на главных направлениях, называются главными осями кривой. Для круга любые направления являются главными и любая пара перпендикулярных диаметров служит главными осями. Главные оси обладают замечательным свойством, к-рое легко усмотреть из ур-ия (6): каждая из осей делит хорды, параллельные другой оси, пополам. Это свойство носит название сопряженности. Всякие два диаметра центральной кривой, делящие хорды, параллельные другому, пополам, называются сопряжёнными диаметрами. Каждая центральная кривая имеет бесчисленное множество пар сопряженных диаметров, вообще не перпендикулярных. Диаметры сопряженные и перпендикулярные—суть главные оси.

Если Ь₃₃ф0, ур-ие (6) легко привести к одному из трех видов:

а^! Ь‘^{= 1} ’ а» Ь> ¹ ’ а^! Ь‘ ¹ ’

где а и b—действительные числа. В первом случае имеем эллипс, во втором гиперболу и в третьем мнимую кривую 2-го порядка, т. к. при действительных ж и у сумма двух квадратов не может равняться^- —1. При Ь₃₃=0 кривая (6) распадается на пару действительных или мнимых прямых. Мы видим т. о., что центральные кривые 2-го порядка, кроме мнимой кривой и случая распадения, дают К. с. (смотрите Эллипс и Гипербола). Если Δ =0, т. e. a_I2=j/a_u V а_гг, кривую (1) нельзя привести к виду (4). Поэтому делаем поворот осей сразу для ур-ия (1). Коэф-ты при старших членах будут те же, что в уравнении (δ). Подставляя α₁₂=V а_и ]/а_тг, получаем:

()^/а_1г cos a -f Va.₂₂ sin a)² ж² + 2 (Va₂₂ sin a +

+ Va_n cos_a) cos a — Va_n sin a) xy +

+ ( Уа_п sin a—Va_2SS cos a)² у² +

+ 2b₁₃ ж + 2&33 у + a₃₃=0.

Выбирая a так, чтобы коэф. при ж² равнялся нулю, т. e. tg α= --!?, получим, что и коэф. «22

при ж у обратится в нуль, и ур-ие примет вид:

где

Ь₂₂ у² + 2b_п х + 2 Ь,₃ у + а₃₃=О,

(7)

^22^6 И б,з —

G&13 ®22 &12 ®2*

(см.

У ^ah + °22

Если центр кривой неопределенный выражения для ж₀, у₀), то

«12 «2₃ «22 «13 ⁼ б,

то есть 6₁₃=0. Ур-ие (7) примет вид:

&22 У² + 2Ь₂₃ У + а₃₃=0, (8)

ИЛИ

(у-у) =

где γ и <5—корни ур-ия (8). Получаем пару прямых, параллельных оси ж, совпадающих в случае γ—δ. Если центр кривой в бесконечности, то Ь₁₃ф0. Перенося начало координат в точку на самой кривой (7), можно уничтожить свободный член; выбираем эту точку так, чтобы при этом исчез и коэф-т при у, x=X+xi; y=Y+y₍; ур-ие (7) примет следующий вид:

&22 Y³ + 2&13×+ 2 (&22 У О + Ь₂₃) У + ^22 Уо“ + + 2 b₁₃ х„ + 2 b₂₃ у₀ + а₃₃=0.

Достаточно решить систему ур-ий &22 &₂₃ ⁼ О

i>222/ό² + 2Ь₁₃ж + 2b_i3y₀ + «₃₃=0, чтобы достигнуть этой цели. Ур-ие (7) примет вид:

6₂₂У² + 2Ь₁₃×= 0,

или

Г²=2рХ,

то есть получим параболу. Точка (ж0, у₀) есть вершина параболы, ось X—ось параболы. Итак и случай Δ =0 приводит, кроме случая распадения на пару параллельных прямых, к К. с. (смотрите Парабола).

Поляра и касательная к К. с. Четыре точки а, Ь, в, d, лежащие на отрезке, называются гармоническими, если

db CL d /Q

6c ~ ” dc ’ *

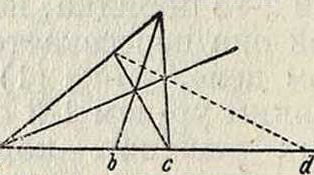
где ab, be, ad, dc—длины соответствующих направленных отрезков. Задавая три точки, всегда можно найти четвертую гармоническую. Если b—середина отрезка ав, четвертая гармоническая d лежит в бесконечности. Во всех остальных случаях она лежит в конечной части прямой. Для нахождения 4-й гармонической можно решить ур-ие (9), или применить геометрии. построение, как указано на фигуре 2 (на основании свойств полного четырех- « угольника). Строя фигура 2.

для каждой секущей прямой из точки М(ж₀, у₀) на плоскости четвертую гармоническую относительно М и двух точек пересечения секущей с кривой (1), получим геометрическое место четвертых гармонических—прямую линию PQ, называемую полярой точки М точка М— полюс по отношению к поляре (фигура 3). Ур-ие поляры имеет вид: а_пжж₀ + а₁₂(жг/₀ + ух₀) + а₂₂уу₀ + а₁₃(х + х₀) + + <Чз(2 + Уо) + «₃₃= б· (10)

Если из двух точек одна лежит на поляре другой, то и другая лежит на поляре первой,

или иначе: если из двух прямых одна" проходит через полюс другой, то и другая проходит через полюс первой. Это свойство, которое называется полярной соп-ряженностыо точек и прямых относительно К. с., легко усмотреть из симметрии ур-ия (10) относит, точек (х, у) и (£С₀, у₀). Поляра точки (ж₀, у₀), лезкащей на самой кривой, есть касательная к кривой в этой точке. Ее уравнение имеет вид (10) при условии, что х₀ и у₀ удовлетворяют ур-ию (1).

Лит.: Власов А. К., Курс высшей математики, т. 1—Аиалитич. геометрия, диференц. и интегр. исчисление, ч. 1, М.—Л., 1925; М лодзеевский Б. К., Основы аналитической геометрии на плоскости, М., 1924; С а л ь м о н Ж., Курс аналитической геометрии двух измерений (конич.сечения), пер. с Франц., Москва, 1908. Ю. Рожанская.