Коноид

Коноид, поверхность, описываемая прямой (образующей) при скольжении согласно какому-либо закону по двум прямым I и т. (направляющим), не лежащим в одной плоскости (название К. указывает на связь этих поверхностей с коническ.; действительно, если направляющие I и т пересекаются, коноид обращается в конус или в плоскость). К. вполне определен, если кроме направляющих I и т дана еще кривая с (направляющая кривая), выражающая закон перемещения образующей по направляющим (смотрите фигура); эти последние в общем случае являются (за исключением образующей в различных ее положениях) единственными прямыми на К., между тем как направляющая кривая см. б. заменена любой другой кривой той же поверхности. Замечателен случай, когда направляющая кривая с тоже обращается в прямую, то есть образующая скользит по трем прямым с I, т; это случай однополого гиперболоида; если же одна из этих прямых удаляется в бесконечность, получается гиперболический параболоид (смотрите Поверхности 2-г о порядка).

В технике обычно рассматривают К., у которого одна из направляющих прямых, наприм. т, лежит в бесконечности; в этом случае образующая в своем движении постоянно пересекает направляющую I и остается параллельною неизменной плоскости μ (н а-правляющей плоскости), к-ройпринадлежит бесконечно удаленная направляющая т. Различают К. прямые и косые, в зависимости от того, будет ли прямая I перпендикулярна к направляющей плоскости μ или не будет. В частном случае, когда направляющая I служит осью ζ и

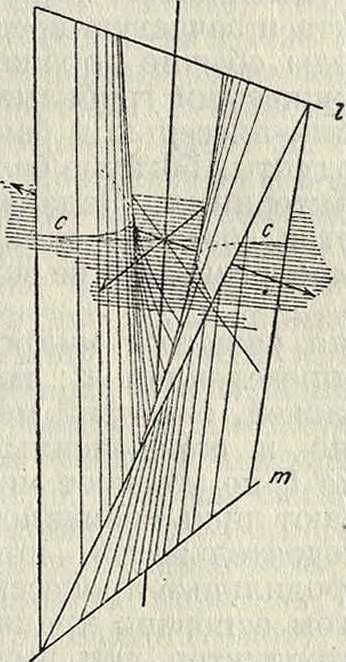
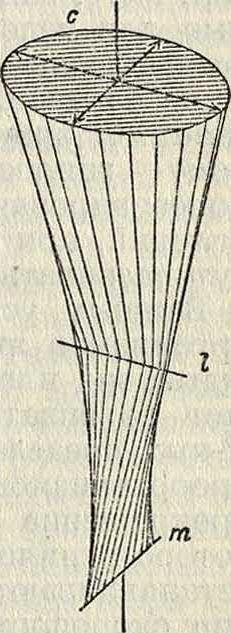
направляющая плоскость μ—координатной плоскостью ΧΟΥ, диференциальное уравнение прямого К. следующее:

^a*_{x +} ^s*y ₌ о,

дх ду ^а ’

а ур-ие в конечном виде ζ=φ

где ψ-

произвольная функция.

К числу прямых К. относится обыкновенная винтовая поверхность (смотрите).

Лит.: Sc hei fers G., Lehrbuch d. darstellenden Geometrie, B. 2, 2 Auli., B., 1927. В. Коновалова.