 > Техника, страница 54 > Конформное отображение
> Техника, страница 54 > Конформное отображение
Конформное отображение
Конформное отображение, соответствие между точками двух плоскостей, при к-ром сохраняются углы между кривыми, выходящими из соответствующих точек, и длины соответствующих бесконечно малых отрезков, выходящих из этих точек, пропорциональны (К. о. есть подобие в бесконечно малых частях).
В теории функций комплексного переменного (смотрите) доказывается, что К. о. осуществляется при помощи аналитической функции; пусть
w=f(z) (1)
такая функция; z=x + iy; разделяя действительную и мнимую части (го—и + iv), мо-ясем написать:
и=и(х,у), v — v(x,y). (2)
Ф-ии (2) осуществляют отображение плоскости (х, у) на плоскость (и, v), конформное во всякой точке, гдef(z) Ф 0. Эти ф-ии мояшо определить и без введения комплексных чисел, как пару непрерывных ф-ий, удовлетворяющих условиям Коши-Римана:
Эи_dv ди _ _ Э»
дх ду ’ ду дх
Из формул (3) в частности следует:
д“и
+§^=Δ“=°; Δ”=0’
(4)
то есть и и v—г а р м о н и ч е с к и е функции (смотрите Потенциал). Наряду с ф-ией (1) К. о. осуществляется также аналитической ф-ией w=<p(x — гу);
при этом отображении величина углов сохраняется, но направление их отсчета изменяется на обратное (К. о. 2-го рода).
V V
ния комплексных чисел (смотрите) показывает, что модуль вектора w получается из модуля г умножением на положительное число R (изменение масштаба), а направление вектора w получается из вектора z поворотом на угол а (преобразование подобия—гомоте-тия с центром в О и вращение на угол а).
2) w— z. Разделяем действительную и мнимую части:
и + iv =
1
х-гу х+гу ’
х“ + у“’ V X* + У2
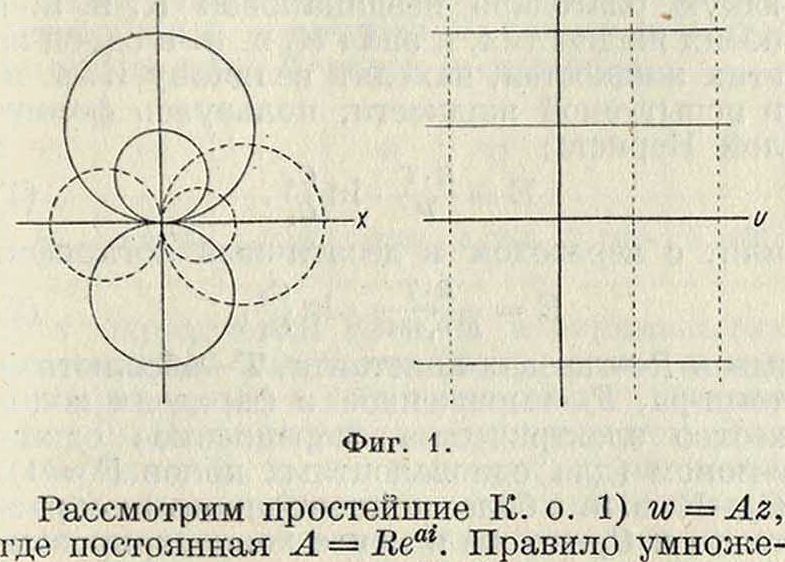
Прямым г“=Const плоскости w соответствуют круги (ж2 + у2 — ~ х—0) плоскости z с центром
^, 0^ и радиусом ; прямым v=Const
соответствуют проходящие через начало координат круги с центрами на оси У (фигура 1). 3) w=z2. Здесь и=х2 — у2, v=2ху. Прямым и —с соответствуют равносторонние гиперболы х2 — у2=с, прямым υ=β—гиперболы 2ху=с, имеющие асимптотами оси координат
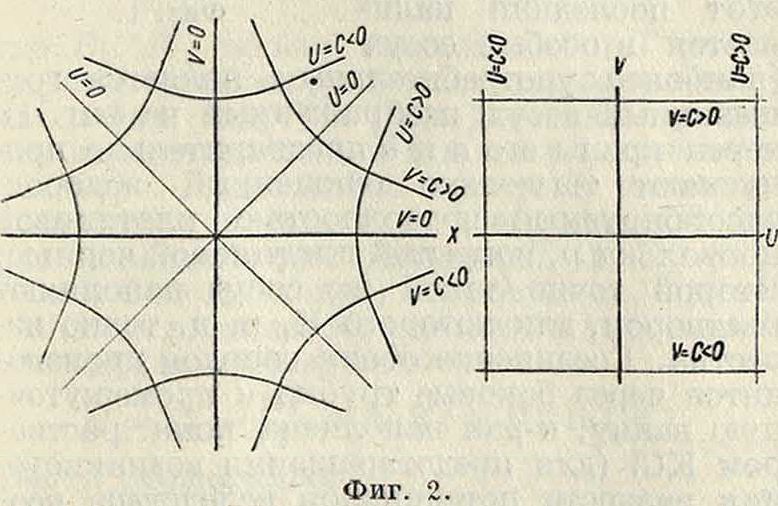
и пересекающиеся с предыдущими гиперболами под прямыми углами (фигура 2). 4) Для той нщ ф-ии w=z2 будем иметь:
У=:;~, гг=ж2 —^ или г>2=4ж2(ж2 — и).
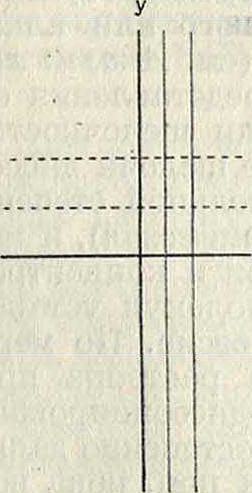
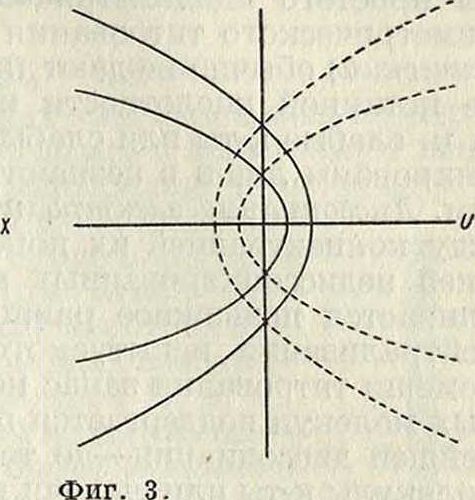
Прямым х—с плоскости z соответствуют на плоскости w параболы, направленные влево, с вершиной в точке и=х2, г>=0 и с фоку сом в начале координат. Аналогично имеем: v2=4y2 (и+У2); прямым у=с соответствуют параболы, направленные вправо (фигура 3).
5) го=In г, z=ew. Предполагая ζ — ρβ’& и iv — u + iv, имеем: oei&=е“*“, Q=eu, & — υ. Эти функции отображают: всю плоскость z на полосу плоскости го, ограниченную прямыми о=0, ν=2π круг радиуса ρ плоскости
z на часть указанной полосы влево от прямой и=In ρ и т. д. 6) w=ζα отображает угол плоскости z с отверстием * на верхнюю полуплоскость w (фигура 4). 7) Эллиптич. инте-
Ζ
ri)aJrW = J^r^-^ отображает прямоугольник плоскости w на верхнюю полуплоскость z. Вообще
w=$(t-a1)ai-1 (ί-α,)β,_1···(ί-α»)βη“1<*<
ϋ
отображает мн-к с углами агл, α2π, ., αηπ в плоскости w на верхнюю полуплоскость ζ
У I v

Фигура 4.
здесь а, а2,., ап и аг, а2,., ап—действительные числа, <Н + а2 -f-. + ап= п— 2 и ак< 2 (/с=1, 2,., п) (формула Кристоф-феля-Шварца).
К. о. применяется в математической физике, теории упругости, гидродинамике. В этой последней, в плоском невихревом движении, существует потенциал скоростей ψ (х, у) такой, что компоненты скорости равны
Функция тока у>(х, у) удовлетворяет ур-иям:
д<р_ду> д<р _ ду>
дх ду 9 ду ~ дх
Это—уравнения (3) и следовательно φ +гу>— аналитич. ф-ия от z—x+iy. Плоскость (х, у) отображается конформно на плоскость (φ,ψ), следовательно данному течению с линиями тока у>(х, у)= Const соответствуют на второй плоскости прямые у>= Const. Часто выбирают и другие переменные.
Лит.: Привалов И. И., Введение в теорию функций комплексного переменного, М.—Л., 1927; В ieberbach L., Einfuhrung in die konforme Ab-bildung, B.—Lpz., 2 Aufl., 1927. В. Степанов.