Координаты

Координаты, числа, определяющие положение точки в пространстве или на плоскости (смотрите Аналитическая геометрия).

К. на плоскости. Декартовы (прямолинейные) К. Берем 2 прямых (о с и К.), пересекающихся под углом со в точке О (начало К.). На каждой оси выбираем положительное направление—на первой (оси абсцисс) ОХ, на второй (оси орди-II а тонн) OY. Для определения К. произвольной точки М проводим линии MP OY и MQ OX; отрезок OP=QM (измеренный какой-либо единицей) дает абсциссу точки М (обыкновенно обозначаемую буквой ж), отрезок OQ= МР=

=у—о р д и н а т у. На фигуре 1 абсциссы вправо от 0 положительны, влево отрицательны, ? ^Λ

ординаты по ложитель- ф_Иг.

ны вверх, отрицательны вниз. Совокупность чисел ж, у представляет К. точки М запись: М(ж, у). Если угол со прямой,имеем прямоугольную систему К., в противном случае—косоугольную.

Преобразование К. Часто бывает необходимо по К. точки в одной системе выразить ее К. в другой. 1-й случай. Новые оси Κ.ΟΧ,ΟΥ соответственно параллельны старым ΟΧ, ΟΥ; К. нового начала О в старой системе (а, Ь) даны. Старые К. точки М(х, у) выразятся (фигура 1) через новые (ж, у) так:

ж=ж + а, _m

У=У + b. ^{ >

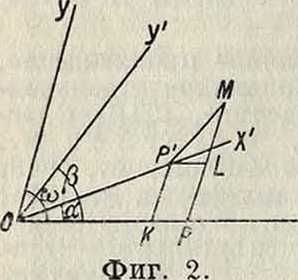
2-й случай. Обе системы имеют общее начало, но разные направления осей. Даны ΧΧΟΥ=ω, ХХОХ=а, ΥΌΧ=β. Старые К. произвольной точки М: х—ОР и у—РМ (фигура 2) связаны с новыми ОР — х и РМ= —у ф-лами (выводимыми из рассмотрения тр-ков ОКР и PLM):

_x Sin (со — α) + y Sin (со - β)

Sin со ¹ /о

_ х Sin а Ч- у^/ sin β W

” Sin СО

В случае прямоугольн. осей (старых и новых) ео=-|-; β—α -)—“ ; ф-лы (2) принимают вид:

ж=x cos а —у sin а, у — x sin а + у cos а.

Общий случай — обе системы имеют различные начала и различные направления осей—сводится к последовательному применению преобразований (1) и (2).

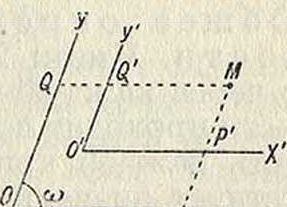
Полярные К. Система полярных К. состоит из точки О (полюс) и полупрямой ОХ (полярная ось). Положение точки Ж (фигура 3) определяется двумя величинами: расстоянием ОМ=г (радиус-вектор) и 2ζ.ΜΟΧ=φ (полярный угол, азимут).

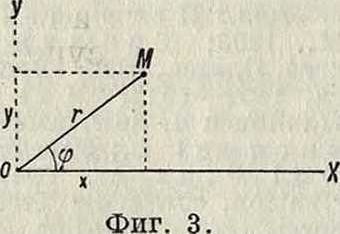
Обыкновенно для φ берут значение между О и 2π. Связь полярных К. с декартовыми. Возьмем О за начало, полярную ось за положительную ось абсцисс и проведем ось ΟΥ перпендикулярно к ОХ. Декартовы К. точки М(х, у) выразятся через полярные:

х=г cosy, у=г sin φ.

Обратно:

г=Vx²+y², tg(p=-_x.

Общее определение К. на плоское т и. Имеем 2 семейства кривых, так что через каждую точку некоторой части плоскости проходит по одной кривой семейства. Пусть каждой кривой 1-го семейства соответствует значение переменного и, кривым 2-го семейства—значения переменного v. Те значения переменных и, v, которые соответствуют линии каждого семейства, проходящей через Ж, будут К. точки Ж (к р и в о линейные К.). В случае декартовых К. оба

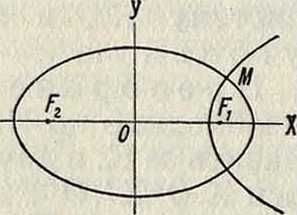
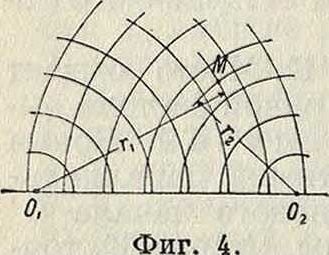
семейства являются семействами прямых, параллельных осям К.; в случае полярных— круги с центром в О и лучи, выходящие из точки О. При биполярных К. положение точки Ж (на верхней полуплоскости, фигура 4) определяется ее расстоянием от 2 точек (полюсов) О_г и 0₂; 0₁ikf=r₁, 0₂Ж=г₂. 2 семейства кривых образованы концентрич. кругами с центрами в 0₁ и 0₂. При эллиптических К. 2 семейства суть софокус-ные эллипсы и гиперболы с фокусами в точках F_x и F₂ (фигура 5); их ур-ие:

ж² i

а2+0 {,2+0 1 (а > о).

Если вместо х, у взять декартовы К. точки Ж (лежащей в положительн. угле XOY), получим для Θ два значения: Я, которое > а² дает эллипс; μ, удовлетворяющее неравенствам Ь² < μ < а², дает гиперболу; Я, μ—эллиптические К. точки М. Связь их с декартовыми К.:

_ («* + *) (а²+/4. „,₂ _(Ь* + Л) (Ь» + аО а2-Ь2 ’ У ь*-а“

К. на поверхности (так называемым Гауссовы К.). К. служат параметры миг), при помощи которых выражаются декартовы К. точек поверхности.—См. Дифференциальная геометрия, формула (10).

К. в пространстве. Система декартовых К. получается из трехгранного угла с вершиной в точке О (начало К.). 3 ребра дают 3 оси ΟΧ, ΟΥ, 0Ζ; плоскости ΧΟΥ, ΥΟΖ, ΖΟΧ называются координатными плоскостями. Плоскости, проведенные через точку Ж параллельно координатным, отсекут на осях отрезки: ОР=х, OQ—y, OR=z х, у, z—К. точки Ж. Обыкновенно применяется сист. прямоугольных К., в которых координатные плоскости взаимно перпендикулярны.

Преобразование координат.

1-й случай (перенесение начала): новые оси параллельны старым; даны К. нового начала в старой системе (а, b, с). Ста- фигура 6.

рые К. выразятся через новые формулами: х=х+а, у=у+Ь, z=z+c. 2-й случай (поворот осей): начало остается прежним, а новые оси образуют со старыми углы, даваемые таблицей (обе системы прямоугольные):

	^х	У	z
X	а	1 *	У
У		β	1 ^y
Z	а"	1 в"	1 Ύ^η

Связь между старыми и новыми К.: х=х cos а + ycosβ + z cos у у=х cos a’ -j- у cos β + ζ cosy z=x cos a" + у cos β" + z cosy";

9 углов таблицы (3) не независимы; между ними существует 6 соотношений;

COS² а + cos² а + cos² а"=1

cos а cos β + cos а cos β + cos a" cos β"=О

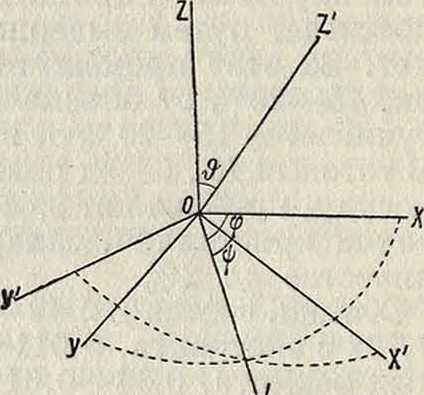
Поэтому положение новой системы можно охарактеризовать тремя независимыми величинами (эйлеровы углы). Эти углы (фигура 6): 1) угол φ, образованный прямою пересечения 0L (двух плоскостей ΧΟΥ и ΧΌΥ) с прямою ОХ, 2) угол #—наклонения этих плоскостей, равный 2ζ.Ζ0Ζ 3) угол у> между 0L и ОХ. Ф-лы преобразования: [х=£C(COS φ COS у — sin φ sin ψ cos #) —

— у cos φ sin у + sin ψ cos у cos #) +

+ «sin φ sin#;

у=cc(sm Ψ COS ψ + COS φ sin у COS #) —

— 2/(sin φ siny — COS φ COS Ψ COS#) —

— zcos φ sin #;

z=a/sin у sin# + ycos у sin# + z cos#. Эйлеровы углы применяются при изучении движения твердого тела. Общий случай (перенос начала и поворот осей) представля-

Фигура 7.

ет собой соединение двух рассмотренных выше преобразований координат.

Цилиндрические К. На плоскости XOY вводим полярную систему К., а координату z не изменяем. Координатами точки М служат τ,φ,ζ.

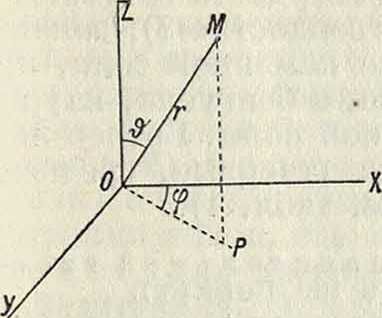
Сферические К. (полярные). Исходя из декартовой системы К., определим положение точки М тремя чи (фигура 7): ОМ=г (радиус-вектор), 2(.Ζ0Μ=& (полярный угол, его дополнение до прямого—широта) и двугранный угол плоскостей ΖΟΜ и ΖΟΧ, равный ХОР=φ (долгота). Три числа (г, φ, &)—К. точки М. Связь сферич. К. с декартовыми К. определяется следующими формулами: х=г sin # cos φ,

У — Г sin # 8ίηφ,

Z=r COS г=Vx² + у² + z².

В последнее время в физике и механике чаще применяется иное расположение осей, а именно: положительная ось ОХ направляется вперед, OY—вправо; это расположение имеет то преимущество, что вращение около оси OZ от ОХ и 0Y совершается против часовой стрелки; такое направление вращения на плоскости обычно принимается за положительное. В. Степанов.

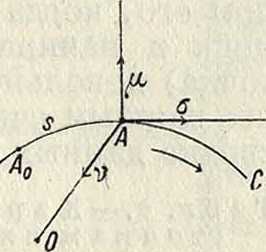
В механике во многих случаях, в особенности при определении кинематич. величин точки, перемещающейся по некоторой кривой двойной кривизны, применяются т. н. внутренние, или натуральные, К. Пусть имеется нек-рая кривая С двойной кривизны (фигура 8). Взяв на этой кривой произвольную точку А, проведем из нее три полупрямые: по направлению касательной в сторону возрастания дуг, по направлению главн. нормали в рассматриваемой точке к центру кривизны О и по бинормали. Полученный таким образом прямоугольный тетраэдр и составляет систему внутренних К. кривой. Каждой определенной точке кривой С соответствует определенное положение внутреннего тетраэдра. Пусть единичные векторы, определяющие вышеуказанные направления касательной, нормали и бинормали, будут соответственно σ, ν и /цтогда, очевидно, имеем:

[σ г]=μ; [г/i]=σ; [μ σ]=ν.

Если s—длина дуги, отсчитанная от некоторого начала А₀, то изменения направлений единичных векторов при переходе от точки А к бесконечно близкой к ней точке определяются следующими ф-лами Серре-Френе (смотрите Дифференциальная геометрия):

Фигура 8.

do 1 άμ ι_ -

ds ρ ⁵ ds o ’ ds

dv 1

σ,

где ρ и ρ суть соответственно радиусы кривизны и кручения в точке А. При пере мещении точки А по кривой С, тетраэдр перемещается определенным образом в пространстве, вращаясь в одно и то же время около касательной (кручение) и около бинормали (изгиб).

При исследовании движения системы точек, находящихся под действием связей, применяются обобщенные, или л а г р а н-ж е в ы, К., при помощи которых выявляются зависимости, существующие между кинематич. величинами различных точек системы. Пусть точка А вынуждена перемещаться по некоторой кривой С. Положение точки в пространстве, определяемое по отношению к некоторой системе отсчета радиусом-вектором г, зависит от некоторого параметра д, определяющего положение точки А на самой кривой. В качестве такого параметра может служить например длина дуги А„А, отсчитываемой от нек-рого начала А₀. Т. о. имеем: г=г (д). Если и сама кривая перемещается в пространстве, то очевидно, что г зависит также от времени (, так что r=r(q,t). Если точка вынуждена перемещаться по некоторой поверхности, то положение точки зависит от двух параметров q₁ и д₂, ^{а П}Р^Иперемещении самой поверхности еще и от времени (, так что

r=r (g₁₍ g₂, ί).

В качестве параметров q_lt д₂ могут служить например К. точки в какой-нибудь криволинейной системе К., взятой на данной поверхности. В общем же случае, если система, состоящая из ν точек, перемещается в пространстве так, что в каждый данный момент точки занимают лишь положения, определяемые ν ф-иями п произвольных параметров q_u g₂,., q_n, а, возможно, еще и времени ί, то положения точек системы определяются радиусами-векторами:

п=Гг (gi, g₂, g₃₎.·, g«,J) (г=ί, 2, з,.,г),

что равносильно наличию 3v равенств:

Хг=Хг (Яи Яг.··,?»,*) 1

Уг=Уг (?1, Яг, — ,ЯпЛ) (г=1, 2, .,Г).

=«< (?1, ?2, — ,ЯпЛ) )

Произвольные параметры q_lt g₂,.,g_n называются обобщенными, или лагранже-выми, К. Число их равно степени свободы системы (смотрите Механика теоретическая). Так, число обобщенных К. для движущегося велосипеда равно 9, а именно: две К. какой-либо точки прямой, по которой пересекается плоскость рамы с горизонтальной плоскостью, одна К., определяющая направление этой прямой, одна К., определяющая угол наклона плоскости рамы с горизонтальной плоскостью, две К., определяющие положение переднего колеса по отношению к плоскости рамы, одна К., определяющая положение заднего колеса, и две К., определяющие положение педалей. Если в уравнениях Лагранжа для какой-нибудь системы, имеющей потенциал L,

£ 9L dt dn)

отсутствуют какие-либо из обобщенных К. q_r, а имеются лишь их производные, то такие К. называются циклическими, отсутствующими или киностэнными, в отличие от К. присутствующих, или видимых. Для первых ур-ия Лагранжа принимают более простой вид: ~=0. В

канонических ур-иях механики встречаются переменные, носящие название канонических К. О К. с точки зрения теории групп см. Инварианты.

Лит.: Млодзеевский В. К., Основы ана-

литическ. геометрии на плоскости, М., 1924; М л о д-зеевский Б. К., Основы аналитич. геометрии в пространстве, 5 нзд., М., 1924. М. Свребреннинов.