> Техника, страница 55 > Кривошипный механизм

Кривошипный механизм

Кривошипный механизм, частный случай четырехзвенного шарнирного механизма., или шарнирного четырехугольника.

Четырехзвенный шарнирный механизм представляет собой шарнирный четырехугольник 0^В0₂ (фигура 1). Неподвижным может быть любое из четырех его звеньев, причем в зависимости от соотношений длин звеньев могут представиться следующие частные случаи: 1) два звена

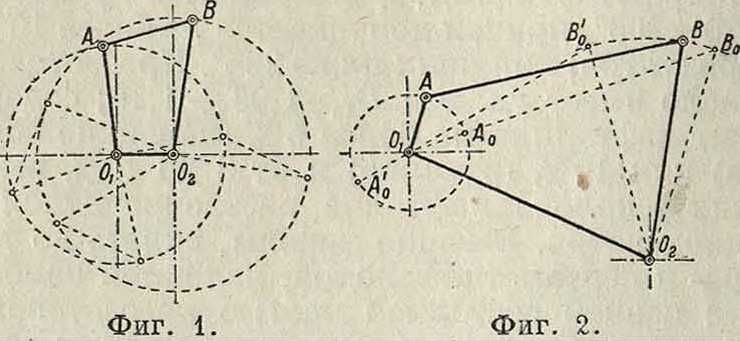
могут описывать полные окружности—двукривошипный механизм (фигура 1); 2) только одно звено может описывать полную окружность, а третье (коромысло) описывает лишь дугу окружности—кривошипно-коромысло-вый механизм (фигура 2); 3) ни одно звено не описывает полной окружности—двукоромы-словый механизм (фигура 3). Если обозначить длину самого короткого звена через г, средних по длине—R и i и самого длинного буквой L, то согласно теореме Грасгофа, если r+L < R + 1, то есть если сумма длин самого короткого и самого длинного звеньев меньше, нежели сум-

_ι й___ i мадлиндвухсредних

7? i звеньев, то механизм

.*—kvi двукривошип-

ч i щ н ы, когда непод-

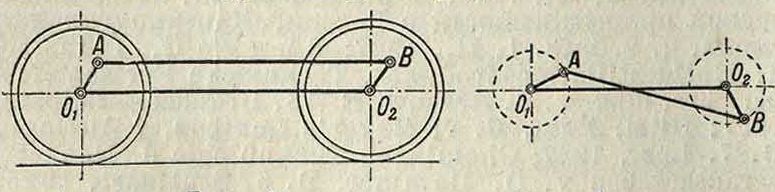
i, пжно самое корот-_фиг i кое звено, и кри-вошипно-коро-мысловый, когда неподвижно звено, смежное с самым коротким. Если r+L> R + l, то механизм двукоромыеловый. Если г=R и L=I, причем равные звенья не смежны, то шарнирный четырехугольник превращается в шарнирный параллелограм, часто применяющийся (в паровозах) для передачи вращения параллельным валам (фигура 4). Если кривошипы все время параллельны друг другу (спарный механизм), то передаточное число равно 1; шатун АВ тогда часто называют спарником. Если равные кривошипы О^А и 0₂В не параллельны друг другу, то вращение их происходит в обратные стороны, и механизм называется шарнирным антипараллелограмом, или антипараллельными кривошипами (фигура 5); передача движения в

Фигура 4. Фигура 5.

этом механизме происходит с переменным отношением скоростей, изменяющимся по такому же закону, как в тождественных эллиптич. зубчатых колесах, оси вращения которых совпадают с фокусами начальных эллипсов. Если же равные по длине звенья смежны, то получаем механизм шарнирного равн обочинка (фигура 6); если в нем неподвижно одно из коротких звеньев, то короткий кривошип может делать два оборота, в то время как длинный кривошип делает один оборот; если неподвиж- но длинное звено, то короткий кривошип также может описать два оборота, в то время как ф_Иг. 6.

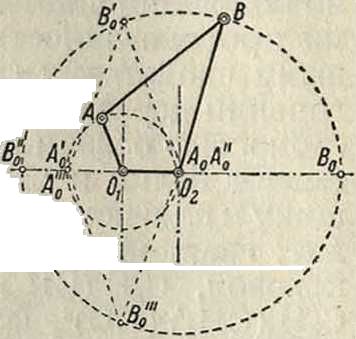
коромысло сделает одно полное качание. Крайние положения Вό и В₀ шарнира В коромысла называются его мертвыми точками; для нахождения мертвых точек засекаем (фигура 2 и 3) из О_г радиусами О_гА+АВ и АВ-ОуА, а из 0₂ радиусами 0₂В+АВ и АВ-0₂В дуги до пересечения с соответственными траекториями. Отсутствие точек пересечения показывает, что данное звено не имеет мертвых точек; на фигуре 2 и 3 мертвые точки обозначены соответственными буквами с индексом 0.

В частном случае, когда центр 0₂ криво-шипно-коромыслового механизма (фигура 2) удален в бесконечность, точка В получает прямолинейное поступательное движение; заменив коромысло О_гВ кинематически эквивалентной парой скольжения, получим К. м. На фигуре 7 представлена схема цент

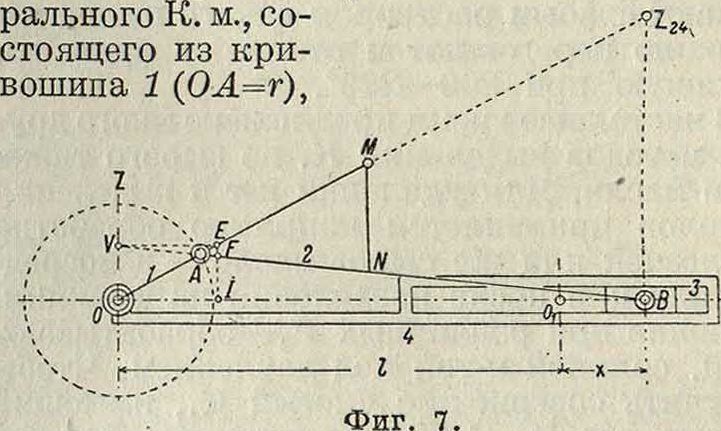
шатуна 2 (АВ=1), ползуна 3 и стойки или неподвижного звена 4. Механизм назван центральным, так как прямая линия ВХ, по которой движется геометрическая ось шарнира В, своим продолжением проходит через точку О. В противоположном случае будем иметь нецентральный К. м. В машиностроении применяются также многие преобразования этого механизма, составляющего главную часть поршневых двигателей и насосов. Если например увеличивать радиус цапфы А или уменьшать радиус кривошипа ОА настолько, что радиус цапфы станет больше суммы радиусов кривошипа и шейки коренного вала О, то получим механизм эксцентрика. Если вместо ОХ стойкой сделать звено АВ, то получится механизм старой пароходной машины с качающимся цилиндром. Если сделать неподвижным звено О А, то получится механизм воздухоплавательного двигателя «Гном» с вращающимися цилиндрами и тому подобное.

Кинематич. исследование механизма фигура7 метров б. выполнено аналитически и графически. Если обозначить отношение длин кривошипа и шатуна через λ=г: I и искать расстояние

<?₁В=ж точки В от среднего ее положения 0_1гвоспользовавшись разложением квадратного корня по биному Ньютона, то

= Г £cOS φ —

(^λ + — 4 ¹ 64

+ “ii +. J

“ 1 024 ;

I + (4 + Ϊ6 +

Ш5, 5Ϊ2~ +--J

COS 2φ -

ί^Λ3+ — +·

(34 ^ 256

• •j COS 4φ +

(в12 ⁺ -

) cos 6у — · · ·

]·

Величина х выражается бесконечным рядом Фурье по четным косинусоидам, причем амплитуды представляют соб по быстро сходящиеся алгебраические ряды от дробной величины Я; обыкновенно Я ^ 0,2, поэтому во многих случаях допустимо пользоваться сокращенным рядом. В самом грубом приближении a;=rcosgp, то есть положение ползуна и поршня определяется проекцией цапфы кривошипа А. Более точно х=г cos <р - -^^Л (1 - cos Ζφ).

Для ψ=0, ж=+ г; для φ=180°, ж=— г, то есть ход ползуна и поршня S=Zr; для <р= 90°,

тХ

χ=— γ, то есть на взмахе поршень не находится в среднем положении.

Графически положения ползуна легко находятся засечками; иногда пользуются биполярной диаграммой проф. Ф. А. Брикса. При вычерчивании в большом масштабе рекомендуется следующее построение (фигура 8): проводим из центра О окружность радиуса г и размечаем ее точками 1, 2 и т. д.; через центр О проводим дугу ΟΥ окружности, радиус которой равен ! и центр которой расположен на ОХ; горизонтальные расстояния точек 1,

.2 и т. д. до этой дуги равны ж; откладывая ι

ОС=ж по ОХ, раз- Фигура 8.

мечаем пути ползуна. Если нужно кроме того знать положение линии АВ шатуна, то строим при точке А угол ВАС=ХСА (точка С изображает положение ползуна, которое соответствует углу поворота кривошипа ХОА). Если кривошип вращается равномерно, делая п об/мин., то <р=cat (где --угловая

-скорость кривошипа). Производная от ж по времени определит тогда мгновенную скорость ползуна

^v “ f=^ro;[-^sin (а +f + If + · · ·) sin2 ωί +

+ (f+ff+-)^sin4co<-E+-)^sin6cui+-}

В самом грубом приближении υ=—τω sin cot, во втором приближении

v=— гш ^sin ωί + sin 2wt j.

Для графического построения мгновенной скорости ползуна (фигура 7) продолжаем АВ до пересечения с линией OZ _L ОХ в точке У, тогда -

ον

v=гео -.,

ОА

то есть отрезок OV изображает скорость ползуна в том масштабе, в каком отрезок ОА изображает скорость пальца кривошипа га>. На фигуре 8 указано то же построение в большем масштабе.

Для определения ускорения j ползуна проводим из точки V линию VE параллельно ОХ до пересечения с продолжением О А; из Е—линию EF параллельно OZ до пересечения с АВ или его продолжением и из F— линию FI перпендикулярно АВ до пересечения с ОХ. Отрезок 01 изображает ускорение j ползуна в том же масштабе, в каком отрезок ОА изображает гео². Аналитически ускорение находим как производную скорости по времени

h 1“ - «4- cos coi— (^;· + у + + · · ·) COS 2cot+

+ + jy + ··· jcos4cui— -]—jcos6cui-f—J.

К. μ., как и всякий четырехзвенный, имеет 6 мгновенных центров, из которых 4 представляют собой сами шарниры: Z₁₄=0; Z₁₂==A; Z₂₃=В; Z_3i лежит в бесконечности в направлении, перпендикулярном к ОХ; построение мгновенного центра Z_2i показано нафигура 7; Z_1S=V.

Если задана сила Р, действующая на поршень по линии его движения, то легко построить эквивалентную касательную силу К, приложенную в А перпендикулярно к О А:

Κ=Ρ·~·

ОА

Для построения (фигура 7) откладывают АМ= =Р, проводят ΜΝ параллельно ΟΖ и получают ΜΝ=Κ. Силы инерции К. м. обыкновенно находят приближенно по весу звеньев, движущихся прямолинейно - поступательно (поршня, штока, ползуна), причем для обобщения результата и сложения с давлениями пара относят вес к 1 см² площади поршня; кроме того к найденному выше весу прибавляют еще 0,3—0,45 веса шатуна, разделенного также на площадь поршня в см²; умножая полученный вес q кг/см² на мгновенное ускорение поршня j и изменяя направление на обратное, получают силу инерции возвратно движущихся частей

b=q I кг/см²,

где з=9,81, если j в м/ск². Существует не-сколько методов точного построения силы инерции шатуна; нек-рые из них описаны в приведенной ниже литературе (смотрите также Динамика поршневых двигателей).

Лит.: Зернов Д. С., Прикладная механика, JI., 1925; Смирнов Л. П., Кинематика механизмов и машин, М.—Л., 1926; Б р и к с Ф. А., Эксцентриковое парораспределение с учетом конечной длины шатуна и эксцентриковых тяг, Москва, 1928; Рерих К. Э., Теория регулирования машин, ч. 1, Маховое колесо и периодическая неравномерность вращения машин, П., 1916. К. Рерих.