Кривые

Кривые. Для изучения свойств кривых математика пользуется методом координат. Задание К. равносильно заданию уравнения, связывающего прямоугольные координаты точек К. Уравнению кривых (в декартовых координатах) можно придать различные формы: у=f (ж) или F (ж, у)=0 или же χ=φ(ί), y=y(t) (смотрите Диференциальная геометрия), причем последняя форма является в теоретических исследованиях и теоретической ме-

ханике предпочтительной, так как она устанавливает равноправность координат хну. В некоторых случаях вместо уравнения К. в декартовых координатах выгоднее бывает рассматривать ее уравнение в криволинейных координатах, чаше всего в полярной системе (смотрите Координаты). Здесь ур-ие К. дается в виде связи между радиусом-вектором ρ и полярным углом со : ρ=/(со) или Φ(ρ, ω)=0. Но классификация кривых проводится по их ур-иям в декартовых координатах. Если левая часть ур-ия F(x, у)= 0 есть целая рациональная ф-ия х и у или м. б. приведена к такому виду, то соответствующая кривая называется алгебраической и порядком кривой называется степень этой целой рациональной функции. Если же функция F(x, у) содержит в себе знаки трансцендентных операций, то кривая F(x, у)=0 называется трансцендентной.

Первый вопрос при изучении кривых—вопрос об установлении ее формы. При этом большую пользу приносит знание расположения ее замечательных точек и положение асимптот. К замечательным точкам относятся точки перегиба, точки прекращения, точки с вертикальными и горизонтальными -касательными и особые точки. Главнейший вид особых точек К.·—кратные точки, в которых К. пересекает сама себя. Простейший пример кратной точки — двойная точка. Координаты двойной точки определяются как общие решения трех,ур-ий:

F(x, у)= о, ||=0, -1=0. (1)

Если эти три ур-ия имеют общее решение х, у, то точка с координатами х, у и будет особой точкой; две касательные в двойной точке определяются из ур-ия:

(у-

у=у у)²=о.

(2)

WJ*_=3C

—у

В зависимости от знака двучлена А=(. ^д1Е

Vдхду) Эх² ву²

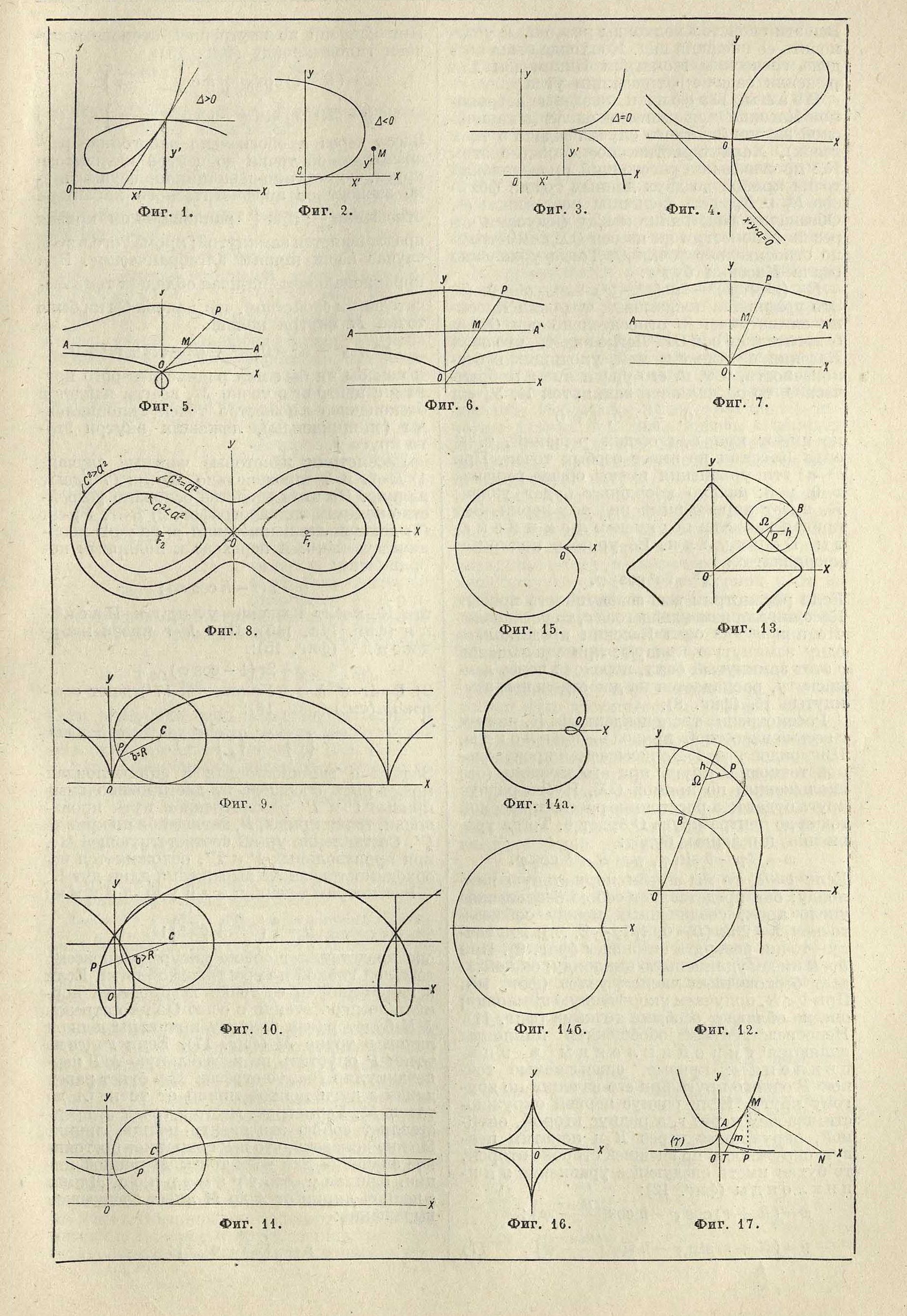
эти касательные действительны и различны при А> 0 (фигура1), мнимы при А < 0 (фигура2) или действительны и совпадают при А=0 (фигура 3). В первом случае особая точка есть узел, во втором—изолированная точка и в третьем—точка возврата. Если в точке (х, у) обращаются в нуль все частные производные от F до порядка к—1 включительно, то имеем k-κ ратную точку. В этой точке пересекается к ветвей К., и касательные к ним даются ур-ием:

Точки перегиба находят из ур-ия

Г=/"(®)=0,

если уравнение К. имеет вид: y=f(x). Для К., заданной ур-ием F(x, у)=0, точки пе региба определяются совместным решением: следующих двух уравнений:

„Л _n /9²F. d²F dF (d^F, 9²F 0F _Λ ,_qvFyX,y) 0, (^2 + dxOyJdy дуЧдж

Координаты точки, в которой касательная параллельна оси ОХ, определяются из урав-dF

нений: F=0, ψ_χ=0; точки с касательными, параллельными оси ΟΥ, находятся из уравнений F=0,=0. Большую услугу оказывает далее знание положения асимптот (смотрите Асимптотическое приблиоюение).

Приложим эти общие соображения к исследованию некоторых К. Рассмотрим д е-картов лист (фигура 4):

F(x, у)=ж³ + у³ - 3аху=0.

Эта кривая—алгебраическая 3-го порядка. Уравнения

^дР=Зу² — 3 ах=0,

= Зж² — bау=0,

дх “ ’ ду ~

F ξ X^s + у³ — Заху=0

имеют общее решение: ж=0, у=0. Найдем затем:

тα= [б£с)_ж=0=с,

у=о

За,

(4>

afF,

Уд’-х)_х=0 ^v’ 9х9у/_ж=0

У=0 “ у=0

(Ш„.-

У=0 ^у

поэтому /1=9а²>0, следовательно декартов лист имеет в начале координат узел. Касательные к ветвям узла можно найти из уравнения (2), принимая во внимание (4); получим: !?/=0, то есть оси координат будут являться касательными к кривой в узле. Правила для определения асимптот алгебраических кривых указывают, что декартов лист имеет одну асимптоту и ее ур-ие: х+у+а=0’. Этого исследования достаточно, чтобы уста^-новить вид К.

Применим те же рассмотрения к к о Ηχο и д е. Конхоидой называется геометрич. место точек, для которых часть МР радиуса-вектора ОР, заключенная между точками М и Р, равняется данной величине I, причем-точка М принадлежит постоянной прямо® А А (фигура 5). Отсюда ур-ие конхоиды:

F=(y — ay (ж² + у²) -=0. (5>

Прямая А А имеет ур-ие у=а. Т. о. конхоида—алгебраич. К. 4-го порядка. Найдем-ее особые точки; совместное решение уравнений (1) показывает, что начало координат—двойная точка кривой. Она будет узлом-(фигура 5), если

Δ=4α² (I² — а²) > О,

при А < 0 она будет изолированной точкой (фигура 6), при А=0—точкою возврата (фигура7). Уравнение (2) здесь примет следующий вид::

Γ(2-α²

Решая ур-ие F= 0 относительно х, найдем:

^х (у-а)2 У ’

следовательно при у=а,х=оо и прямая у=а будет асимптотой конхоиды. Уравнение (5)-содержит лишь четные степени ж, а потому-конхоида симметрична относительно оси ОГ„

Фигура 2

Фигура 6

Фигура 12

Фигура 16

	___Р
	м!


0

	[ х с
	Ук“		-X

	^у 1 ^/Δ=0
		У
0	X



V V V ^

	aJ.
(п	W/n:
~0	г я /у

Все эти свойства конхоиды позволяют установить ее внешний вид. Конхоида была введена греческим геометром Никомедом для решения задачи о трисекции угла.

Овалы Кассини введены астрономом Кассини для решения одной механической задачи (частного случая задачи о трех делах). Характеристическое свойство этих К.: произведение расстояний произвольной точки кривой до двух данных точек, фокусов и Р₂, есть величина постоянная с². Обозначим расстояние между фокусами через 2а и поместим их на оси ОХ симметрично относительно точки О. Тогда уравнение овала Кассини будет:

F=(ж² + г/²)² - 2а² (ж² - у²) + а⁴ - с⁴=0. (6) Это уравнение показывает, что овал Кассини симметричен и относительно оси ОХ и относительно оси OF. Легко видеть, что овал Кассини не имеет ветвей, уходящих в бесконечность, и т. к. его уравнение алгебраическое, то он является замкнутой К. Ур-ия

^=0, Щ= О, F= О

не имеют при сфа общих решений, то есть •овал Кассини не имеет особых точек. При «²=а² эти уравнения имеют общее решение ж=0, у=0; начало координат будет узлом; К. имеет характерный вид восьмерки. Эта кривая известна под именем лемнискаты Б е р н у л л и. Ее ур-ие в полярных координатах:

ρ²=2α² cos 2<р.

Если рассмотрим всю совокупность кривых Кассини для изменяющегося с то установим, что при с²>а² овал Кассини представляет одну замкнутую кривую; при уменьшении •с этот замкнутый овал, переходя через лемнискату, распадается на две отдельные замкнутые К. (фигура 8).

Рассмотрение трансцендентных К. начнем с весьма известной кривой — циклоиды. Циклоидой наз. К., описываемая произвольной точкою Р круга при его качении (без скольжения) по прямой ОХ. Пусть радиус круга будет R, а расстояние рассматриваемой дочки до центра круга С будет b. Тогда уравнение циклоиды будет:

ж= R<p — b sin <р, y=R-bcos<p.

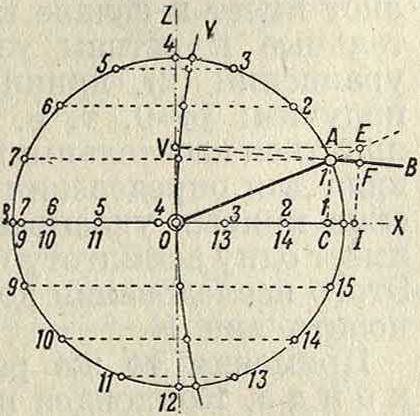
Если b=R, то мы имеем нормальную циклоиду; она представляет собою бесконечное число арок, соединенных между собою в точках х=2лк (к=0, + 1, + 2, .); эти точки—точки возврата циклоиды (фигура 9). При b > R имеем удлиненную циклоиду; она обладает бесконечным числом узлов (фигура 10). При b< R, получаем укороченную циклоиду; она не обладает особыми точками (фигура 11). Непосредственным обобщением циклоиды являются гипоциклоиды и эпициклоиды: кривые, описываемые точкою Р одного круга при его качении по другому кругу. Если радиус первой окружности назовем через г, а радиус второй, опорной, окружности через R и покатим первую окружность по внешней стороне второй, то будем иметь следующее уравнение эпициклоиды (фигура 12):

х=(й + г) cos φ — h cos ;

у=(R + r) sin ψ - h sin ?>J. (7)

При качении по внутренней стороне получаем гипоциклоиду (фигура 13):

x=(R-r) cos φ -f h cos ;

у — {R — r) sin φ — h sin (^R~- ψ j. (7)

Здесь через h обозначено расстояние рассматриваемой точки до центра катящегося круга. Форма гипо- и эпициклоид существенно зависит от арифметического характера отношения у; при у рациональном кривая представляется замкнутой; кроме того в этом случае наши кривые алгебраические. При R

иррациональном у кривая обладает тем замечательным свойством, что,какова бы ни была точка М внутри кольца

x²+y^z-Rⁱ=0, ж² + 2/^а — (R ± г)²=0

и как бы ни был мал радиус нек-рого круга у с центром в точке М, всегда найдется бесконечное множество точек гипоциклоиды (эпициклоиды), лежащих внутри этого круга у.

Рассмотрим некоторые частные случаи. 1) R=2r и h—произвольно. Ур-ия (7) дают эллипс. На этом свойстве основано устройство нек-рых эллипсографов. 2) R-r. Ур-ия (7) дают после исключения φ, замены координат x=x+h и перехода к полярным координатам:

ρ=2 (r — h cos си);

эта К. носит название улитки Паска-л я (фигура 14а, 146). При имеем кардиоиду (фигура 15):

ρ=2г (1 — cos ω).

3) R=4r и h=r. Уравнения (7) дают астроиду (смотрите) (фигура 16):

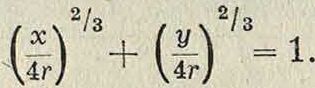
Задача о гипоциклоидах и эпициклоидах может быть обобщена на две произвольные кривые Г и Г рассмотрением пути произ-вольн. точки кривой Г, катящейся по кривой Г. Составление ур-ий соответствующей К., при произвольных Г и Г, осложняется необходимостью знать выражения длин дуг К.

Рассмотрим теперь цепную линию:

У=2 I^е “ + ^е

она представляет собою фигуру равновесия тяжелой гибкой и нерастяжимой нити. Если в какой-нибудь ее точке М провести нормаль до пересечения с осью ОХ, то отрезок MN будет равен радиусу кривизны цепной линии^-в точке М (фигура 17). Если далее из точки Р опустить на касательную МТ перпендикуляр Pm, то отрезок Mm будет равен длине s дуги цепной линии от точки А до точки М. Геометрии, место у точек m представляет собою эвольвенту цепной линии. Можно доказать, что тР сохраняет постоянное значение для всех точек М цепной линии. Кривая у есть трактриса. Длина s цепной линии от А до М имеет следующее выражение:

_а г ^х —^я

s=-₂[e^a.-e «];

•отсюда уравнение трактрисы будет:

х_х=a cos 9 + a In tg ®, *

j/j=asin6.

Трактриса имеет в точке Л точку возврата и ось ОХ своей асимптотой.

К семейству трансцендентных К. принадлежат и спирали. Под спиралями понимаются обычно К., делающие бесконечное число оборотов около какой-нибудь точки. Простейшим примером служит архимедова спираль (смотрите):

= αφ.

Более сложные примеры дают гиперболическая спираль (фигура 18) г=

=-Г и логарифмическая спи-

Ф ага раль г=е^ач’. Гиперболическая спираль обладает следующими свойствами: она имеет асимптоту у=к, к которой приближается при φ -> 0, и имеет далее точку (0,0) в качестве асимптотической точки. Характерным свойством ло-гарифмич. спирали является ее неизменяемость при преобразовании подобия с центром в точке О. К разряду спиралей относятся и кривы е Френеля, встречаемые в теории диф-фракции (смотрите Диффракция):

^ж=/^с°^з y=f^sin^^ds·

О О

Хотя входящие сюда квадратуры взять и невозможно, но можно тем не менее составить представление о форме К. При s-> + со К. делает бесконечное число оборотов около

(α νπ а V л

---, —1, a при s-+— оо она делает бесконечное число завитков около точки

(а Ул а Ул

"i^-’ 2

Тригонометрические К.—см. Тригонометрические функции.

Лит.: Гу р с а Э., Куре математического анализа, т. 1, М., 1911; Е г о р о в Д. Ф., Диференциаль-ная геометрия, М.—П., 1924; Lor ia G., Spezielle Algebraische und transzendente ebene Kurven, 2 Auli., В. 1, 2, Lpz.—B., 1910—1911; W i e 1 e i t n e r H„ Theorie d. ebenen algebraischen Kurven hoherer Ord-nung, Berlin, 1905; Hilton H., Plane Algebraic Curves, Oxford, 1920. Л. Сретенский.