> Техника, страница 56 > Критическое состояние

Критическое состояние

Критическое состояние, состояние двухфазн. (замкнутой) системы веществ, при к-ром малое повышение ί° в системе вызывает исчезновение различия между фазами.

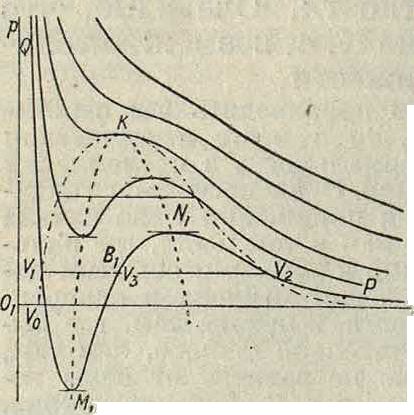
Однокомпонентная система с фазами: жидкость и пар. При нагревании жидкости в закрытой трубке в зависимости от отношения объёмов жидкости и сосуда возможны три случая: 1) вся жидкость превращается в пар, 2) вся трубка заполняется жидкостью, 3) при определенной критической темп-ре (Т°_крит=1°_криот.+ +273,2) м е н и с к, то есть поверхность раздела фаз, исчезает; этой темп-ре отвечают определенные критич. давление р_крит. и критич. уд. объём v_Kpum, (смотрите Критические явления); система находится при этом в К. с. При t° >1°хрит. система находится в газообразном состоянии и никаким давлением не м. б. превращена в жидкость. Теоретически К. с. может наступить при строго определенном количестве вещества в трубке, определяемом критич. уд. объёмом v_Kpum/, практически К. с. наблюдается и при значительных отклоне-. ниях объёма трубки от того, к-рый отвечал бы критич.объёму, причем если объём трубки меньше критического, то исчезновение мениска происходит выше середины трубки, и обратно. Объясняется это явление действием силы тяжести на систему в К. с. На изотерме, отвечающей /%_Мт.(фигура 1) в крит. точке (р=Рк_Рит. и »=v».), касательная к изотерме параллельна оси абсцисст_крит на этом отрезке изотермы сжимаемость си стемы (fjj)_r огромна, вследствие чего под влиянием силы тяжести критическое состояние может наступить на определенной высоте, между тем как выше этого места плотность заметно меньше, а нижд — заметно больше критич. плотности. Очевидно, что опытное осуществление К. с. возмсжно только благодаря силе тяжести.

Если нагревание трубки производить без перемешивания ее содержимого, то в месте исчезновения мениска наблюдается ненормальность в преломлении света, сохраняющаяся и при 1° на несколько градусов выше, чем t°Kpum.; при понижении t° до пачала конденсации образуется туман в том месте, где раньше был мениск; косвенными и прямыми опытами доказано, что после исчезновения мениска в однородной на вид системе плотность вещества там, где была раньше жидкость, значительно больше, чем там, где был пар; это различие не зависит от силы тяжести, так как наблюдается и в U-образной трубке. Эти ненормальности с течением времени сглаживаются, но полностью пе исчезают; очевидно, что момент исчезновения мениска не отвечает устойчивому К. с., которое наступает или по истечении длительного времени или при помешивании системы; отметим, что, чем чище вещество (отсутствие примеси постоянных газов), тем менее резко выражены эти ненормальности, однако полностью объяснить эти явления примесями едва ли возможно. В случае равновесного К. с. при t° немногим выше t°_Kpum. наблюдается голубая, а при охлаждении белая опалесценция. Смо-луховский показал, что это явление объясняется неоднородностью газа, то есть флуктуациями (колебаниями) его плотности в критической области.

В К. с. системы жидкость—пар: 1) —

конечна, 2) (v₂ — ν,)= Δυ=0; 3) полная и внутренняя скрытые теплоты испарения равны 0, то есть теплота перехода из жидкого в парообразное состояние равна нулю и не только объёмы, но также и энергия жидкости и пара равны. При 1°_ктш. поверхностное натяжение σ жидкости обращается в нуль (Д. И. Менделеев).

Возможность существования перегретой жидкости и переохлажденного пара привела Джемса Томсона к мысли о теоретич. непрерывности изотермы системы жидкость— пар; простейшее выражение эта мысль нашла в теории, и в частности в ур-ии Ван-дер-Ваальса:

(р+Й. (»-Ь)=ЛТ,

где а и Ь — индивидуальные постоянные вещества и R — газовая постоянная. На фигуре 1 изображены: практическая изотерма QViV₂P (QVi—ветвь жидкости, V₂P—ветвь пара, V_XV₂—разрыв сплошности) и теоретич. изотерма QV _гВ,2V₂Р, где ветвь V₁M₁

отвечает метастабильному состоянию жидкости (перегретая жидкость), ветвь V₂N₁— такому же состоянию пара (переохлажденный пар), ветвь M₁B₁N₁—лабильному (нере-ализируемому) состоянию системы. Каждой ί° отвечают три уд. объёма: ν_±—жидкости, ν₂—пара и ν₃—лабильного состояния. При повышении f° разрыв сплошности уменьшается и в критической точке сходит нанет; здесь все три уд. объёма сливаются.

К. с. характеризуется строго определенными значениями t° и давления; следовательно с точки зрения правила фаз такое состояние является нонвариантным, к-рое требует в однокомпонентной системе наличия трех фаз; здесь мы имеем предельный случай слияния трех фаз: жидкой, лабильной и парообразной; экспериментально лабильное состояние системы жидкость—

пар реализуется только в К. с. Факт существования К. с. как нонвариантного доказывает правильность концепции о теоре-тич. непрерывности изотермы системы жидкость—пар. С термодинамич. точки зрения вся ветвь QM₁ (фигура 1) отвечает устойчивому равновесию, причем QV i—стабильная, V₁M₁—метаста-бильная часть с точки зрения опыта; то же относится к ветви пара jV^jP. Положение прямой ViVz, то есть точек разрыва, определяется правилом Максвелла (вытекающим из второ-Фигура 1. го начала термоди намики), по которому площадь У_хМ^у_з равна площади V₃Геометрическое место точек, аналогичных точкам Fj и F₂,—кривая V₀KV₃—носит наименование граничной, или б и иода л ь н о й, кривой (бинодаль). Точки,

аналогичные М₁ и N_lt в которых (§f)_T= О,

являются границами устойчивого и неустойчивого состояния системы; геометрическое место их—кривая M₁KN₁—для однокомпонентных систем является спинодаль-ной кривой (спинодаль). Бинодаль и спинодаль соприкасаются в критич. точке.

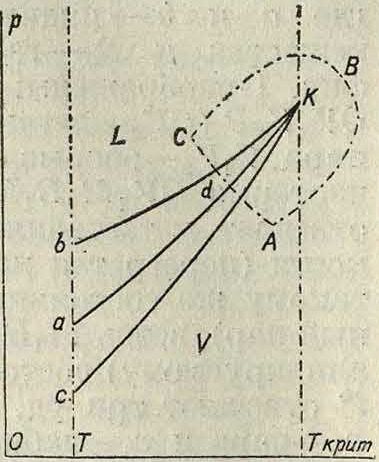
Непрерывный переход от жидкого к па-ро-(газо-)образному состоянию возможен не только теоретически по изотерме, но и опытным путем—путем обхода вокруг критич. точки: нагреваем пар в точке JP при постоянном объёме; при t° выше критической уменьшаем объём при давлениях, больших чем VKpum., придем в точку Q, где система находится в жидком состоянии; на этом пути от пара к жидкости нет разрывов сплошности в свойствах системы. Еще рельефнее это явление сказывается на диаграмме температура—давление (фигура 2). Здесь аК— кривая упругости пара данной жидкости (устойчивое стабильное равновесие жидкости и пара), ЬК— граничная кривая метастабильности пара, сК—то же жидкости.

В области V существует только пар, в области L—только жидкость. Выше Т°_критсостояние системы— газообразное. Кривые оканчиваются в кри-тическ. точке К; с ма-тематич. точки зрения точка К есть особая точка, что вызывает ряд особенностей в свойствах ф-ий от р и Т, например многозначность термодинамической ф-ии ζ в области ЬКс. На фигуре 2 показаны два опытных перехода от пара к жидкости: прерывный АС и непрерывный АВС.

Однокомпонентная система с твердой (кристаллической) и жидкой фазами. По вопросу о существовании К. с. такой системы мнения расходятся. Пойнтинг, Планк, Оствальд, Ван-Лаар высказываются за существование такого состоянияв области очень высоких температур и давлений; Тамман и его школа—против. Тамман дал теорию максимума, согласно которой кривые взаимного превращения твердой и жидкой фаз должны быть замкнутыми кривыми, следовательно кривая плавления должна проходить через максимум. Опытные данные в пределах до <° 200° и до 10 000 к г/см² давления не решают вопроса. С термодинамической точки зрения критич. теория основывается на допущении единой ^-поверхности для данного вещества; существование различных фаз — результат многозначности f-поверхности, геометрически—результат самопересечения поверхности. Теория Таммана основывается на допущении независимости f-поверхностей разных твердых фаз данного вещества. Одна термодинамика решить спора не может, так как обе теории ей не противоречат.

Двукомпонентная сист.ема сфазами: жидкост ь—п а р. С

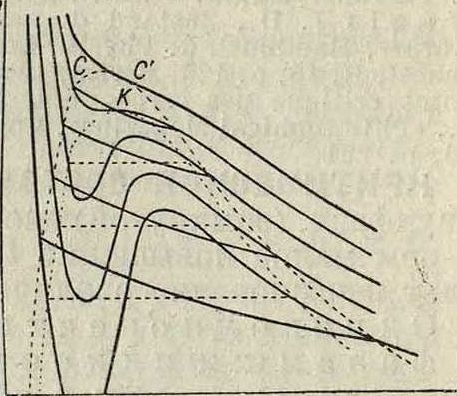
точки зрения правила фаз К. с. бинарных смесей моновариантно (два компонента и три слившихся фазы), откуда вытекают крупные отличия К. с. таких систем от К. с. индивидуального вещества. Фигура 3 показывает в диаграмме (р, υ) изотермы бинарной смеси; особенности здесь следующие. Кривые разрыва сплошности (переход от жидкости к пару) не горизонтальные прямые, а кривые высших порядков; это отвечает факту, что составы жидкости и пара бинарной смеси при данных темп-ре и р различны, при данной 1° жид-кость и пэ.р ОДИ- Фигура 3.

накового соста-

ва обладают разными давлениями. Критич. точек у бинарной смеси две. Первая критич. точка С, в ней состав и плотности обеих фаз совпадают, то есть обе фазы делаются идентичными, однако это происходит не при наивысшей ί°, при которой существуют двухфазные состояния. Крайняя изотерма, отвечающая ί°, выше которой существует только газообразное состояние, касается граничной кривой (бинодали) во второй критической точке С. Точечная кривая, проходящая через К, показывает изотермы мыслимого индивидуального вещества с теми же константами Ван-дер-Ваальса, которые свойственны данной смеси. В случае индивидуального вещества спинодальная кривая—граница устойчивых состояний—совпадает с кривой—геометрии. местом точек, где (|f)_y⁼0; У бинарных смесей это две отдельные кривые. Спинодальная кривая, отделяющая устойчивые состояния от неустойчивых, соприкасается с би-нодальной в первой критич. точке; кривая

(H)_y=0 у смесей полностью лежит внутри I спинодальной кривой.

На фигуре 4 показано, как изменяются уд. объёмы V с составом смеси (х—концентрация второго компонента смеси) при данной темп-ре t (р—переменно) в критич. области. Здесь взята Г, которая превышает t°_Kpum. ряда смесей, богатых более летучим вторым компонентом. Прямые типа р,р₂, q₁q₂, r₁r₂—т. н. н о д ы, или к о н н о д ы, соединяют составы и удельные объёмы жидкости и пара, находящиеся в равновесии: жидкости р, отвечает пар р₂. При переходе к смесям, более богатым вторым компонентом, ноды сильно изменяют направ-

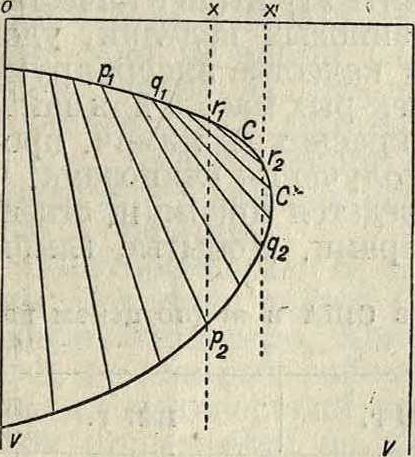
Фигура 4.

верхняя влево от ление, становятся все короче и схо-дят нанет в первой критической точке С. Вторая критич. точка С отвечает двухфазной смеси с максимальным содержанием второго компонента при данной темп-ре. Нижняя ветвь бинода-ли до С—граница стабильного пара,

__.. __ С—граница жидкости.

Раздвоение критической точки у бинарных смесей влечет за собой следующее следствие для смесей, состав которых лежит между составами, отвечающими точкам С и С. Возьмем пар смеси состава х в состоянии, отвечающем точке ниже q₃, и подвергнем его изотермическому сжатию. Под влиянием давления объём пара станет уменьшаться, в точке qа появятся первые капли жидкости состава q_t· по мере повышения давления (уменьшения объёма) количество ^жидкости сначала будет увеличиваться, пройдет через максимум, потом станет уменьшаться, и наконец в точке г₂ жидкость исчезнет, так как г₂ лежит на парообразной ветви бино-дали. Такого рода явление носит название обратной конденсации первого рода.

Пример. Смесь хлористого метила, СН,С1, и углекислоты, С0₂, (состава 41% С0₂; 69% СН₂С1) при 105° (р—давление в atm, υ—объём жидкости, г·,— общий объём пара и жидкости в см³): р в atm.

Vl в см³

V в см³.

73,3	77,2	81,8	82,4	83,1	83,5	83,8
117,9	99,6	81,0	78,6	77,3	75,4	74,0
0	3,9	8,6	7,6	4,3	2,8	0

В тех случаях, когда вторая критическая точка G лежит выше первой С, у смесей между С и С наблюдается обратная конденсация второго род а: в результате изотермическ. повышения давления на жидкую смесь образуется пар, его количество проходит через максимум, потом он исчезает. Такие случаи более редки и труднее наблюдаемы (например: вода-(-пропил овый ).

Из ряда других особенностей отметим еще следующее баротропич. явление. Направление жидкой ветви бинодали и взаимное положение критическ. точек С и С м. б. таким, что точка C будет на диаграмме справа, но выше С; тогда крайние ноды будут наклонены вниз не слева направо, а обратно; это значит, что пар, находящийся в равновесии с жидкостью, удельно тяжелее жидкости и жидкость будет плавать на слое газа. При мер: в смеси водорода и гелия при —253° и 49 atm жидкая фаза плавает на газовой.

Для целей техники явления К. с. в области смесей (сжижение газов) более важны, чем такие же явления у индивидуальных веществ, так как с последними техника имеет дело крайне редко. Изучение, этой области требует знакомства с учением о термодина-мич. поверхностях. Явления К. с. в случае тройных смесей, где оно бивариантно, очень сложны; начало их изучения положено трудами Ван-дер-Ваальса. См. Газ.

Лит.: РаковскийА. В., Теоретические исследования по вопросу о взаимных превращениях фаз, «Вестник Ломоносовского физ.-хим. об-ва», М., 1926,т. 2, вып. 2; Van der WaalsJ.D. u. Kohnstamm Ph., Lehrbuch d. Thermostatik, В. 1, 2, Leipzig, 1927; К u e n e n J. P., Theorie d. Verdampfung u. Verfliis-sigung von Gemisehen u. d. fraktionierten Destination, Lpz., 1906. А. Раковский.