> Техника, страница 56 > Кручение

Кручение

Кручение, один из основных видов деформаций и напряженного состояния, рассматриваемых в науках сопротивление материалов (смотрите) и теория упругости (смотрите). Кручение возникает, когда брусок подвергается действию пары сил, плоскость которой перпендикулярна к оси бруска. Момент пары называется крутящим моментом. Деформация К. заключается в относительном повороте параллельных сечений бруска. Мерою деформации служит изменение угла между прямыми, лежащими в двух параллельных сечениях и перпендикулярными к оси бруска. Величина изменения этого угла называется у г л о м К. на длине Ϊ, где I—расстояние по оси бруска между двумя рассматриваемыми параллельными сечениями.

К. круглого бруска. Опыт дает следующие показатели: 1) параллелизм сечений не нарушается; 2) прямые линии в плоскости (в частности и радиусы сечения) не искривляются; 3) расстояния между сечениями не изменяются; 4) величина угла кручения пропорциональна расстоянию между се чениями и крутящему моменту. Отсюда выводы: а) объём бруска сохраняется неизменным, б) брусок испытывает только сдвиг, к-рый не сопровождается растяжением или сжатием (чистый сдвиг). Пусть при расстоянии dx (фигура 1) между сечениями А и В, сечение В при кручении поворачивается на

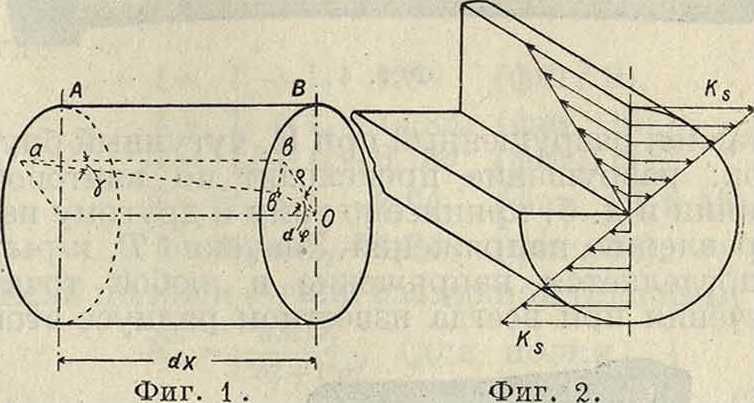
угол кручения άψ. Волокно аЬ займет положение аЬ, образуя с прежним направлением угол сдвига у. Пространственная фигура abb с достаточной точностью м. б. принята за плоский тр-к. Поэтому ~~bb= ab tg у или (вследствие малости углов)

—bb=y-dx. (1)

Но из сектора Оbb следует:

~bb=Q-d<p, (2)

где Q—радиус поверхности цилиндра с образующей ab. Сравнение (1) и (2) приводит к соотношению:

КЗ)

где Т—угол кручения на единицу длины бруска. В соответствии с 4-м опытным положением этот угол сохраняет, постоянство при определенном действующем моменте. Считая напряжения и деформации (как и в иных случаях) пропорциональными, имеем напряжение при К.: I

Kir GqT. (4)

Здесь, G—м одуль сдвига материала. Т. обр. напряжения изменяются, по закону прямой линии, в центре сечения они равны 0, на периферии достигают максимума и в каждом сечении зависят от расстояния рассматриваемой точки до центра; взаимное расположение точек вдоль оси остается без всякого влияния на их напряженное состояние.

Фигура з.

Касательные напряжения, возникающие при К., обладают свойством двойственности: они появляются одновременно по двум взаимноперпендикулярным плоскостям, в каждой точке их общей линии сечения имеют два направления и равны по величине (фиг^2). Напряжения обоих направлений м. б. обнаружены при опытах на кручение по получаемым при этом формам разрушения скручиваемых брусков. На фигуре 3 изображено· разрушение деревянного бруска: долевые трещины должен быть отнесены за счет долевых касательных напряжений, которым дерево ела-

бо сопротивляется. На фигуре 4 изображено разрушение мягкого железа: здесь разрушение произошло из-за действия поперечных касательных напряжений. На фигуре 5 пред-

Фигура 4.

ставлен разрушенный при К. чугунный брусок: разрушение происходит по винтовой линии и должен быть приписано тому и другому направлению напряжений. Значение Т, которым определяется напряжение в любой точке сечения при всегда известном радиусе этой

Фигура 5.

точки, отыскивается по условиям равновесия отрезанной части бруска. Из равенства моментов—крутящего и внутренних сил—· относительно оси вращения имеем:

M_s= f K_so dF

(F)

или согласно (4)

M_s=J Gq^T dF=GT f q

(F) (F)

T. к. G и T—константы. Интеграл J₀=f&

(F)

называемый полярным моментом инерции сечения и равен для кругового сечения

nd⁴,

dF,

(5)

dF,

Jo-

32

(6)

где d—диаметр круглого бруска(смотрите Момент инерции). Поэтому угол кручения на единицу длины

^Т=тЛ- <⁷>

Напряжение в точке радиуса ρ равно по (4)

Щд

До ’

а для периферии цилиндра, при ρ= d/2,

Т7~ ^MS d/2

j-*- Ο ΊΎ (IT. τ

(8)

О)

Частноеназывается моментом

(модулем) сопротивления при К. и обыкновенно обозначается W₀. Окончательно имеем:

м.

К.

s max —

(10)

Это выражение представляет собой уравнение прочности при К. круглого бруска, если под K_{s max} разуметь допустимое напряжение на К. Угол К. на длине t равен мл.

J oG’

(И)

ур-ие (11) называется ур-ием деформации круглого бруска. Ур-ия (10) и (11) могут служить каждое в отдельности для определения размеров круглого сечения, причем в уравнении (10) размеры определяются по соображениям прочности (наибольшее допустимое напряжение), в ур-ии (11)—по заданной деформации (наибольший угол К.). Пользуются тем и другим ур-ием для различных условий работы. Трансмиссионные валы рассчитываются или по деформации или по условиям прочности—в зависимости от того, какой способ расчета дает больший размер. Для трансмиссионных валов допустимое напряжение K_s=200 килограмм/см допустимая деформация ¹/₄° на п. м. Коренные валы рассчитываются по условиям прочности, но обязательно подвергаются проверке и на деформацию (смотрите Валы).

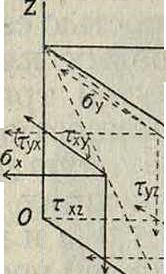
К. брусков некруглого сечения. Решение этой задачи сложно и элементарным путем невозможно. Практич. значение ее очень велико, а особенно для тел прямоугольного сечения, так как плечи кривошипов и буферные пружины являются такими телами. Основные этапы решения следующие. Выделяем безконечно малый параллелепипед из скручиваемого тела. Напряженное состояние его изображено на фигуре 6. Условия равновесия будут следующие:

т =т zxf ^vyz ^Lzy>

_|_ ¹

V-

nN.
	-
j
т-л.у У	чХ 0 ух

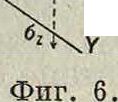
^τχ?. ~ дх-

дх

xy 1 dx_xz __ А

ду "и м д°у, д ду “г дг

dx_v

до_г, дх. дг ‘

yx i ^итуг _ а дх ^ дг _!_ ^dzv

дх

4®=о. ду

(12)

-напряжения, которые показаны на фиг! 6. Также должен быть соблюдены поверхностные условия: a_xcos(x, n) + T_x,jCOs(y,n)+T_xzcos(z, η)=0,1 a_ycos(y,n) + r_xycos(x,n)+T^cos(z, n)=0, (13) a_z cos {z, n) + T,_/zcos(y,n)+T_xzcos(x,n)=0.) С.-Венан (St.-Venant) принял допущение: 1) σ_χ=a_y=σ_ζ=б, 2) х_ху=0—все нормальные напряжения, также касательные в перпендикулярной к оси бруска плоскости, равны 0. Из ур-ий (12) и (13) остаются в силе:

д^хг i дтуз _ q

ду ’

дх

^vyz

cos (у, η) + τ_χζ cos (ж, п)=0.

Если положить ду д<р дх ⁹

(14)

(15)

где ψ—ф-ия переменных ж и у и называется ф-ией напряжений, тогда уравнения (14) получат вид:

д²<р d²q>

дхду дцдх

= о,

ибо

I £?) (_ _L

дх) ds) "F ду

ds

= 0,

cos (у, w)=-§, cos (ж, И)=J-,

причем <te—элемент контура сечения. Таким обр. φ (х, у) имеет на контуре сечения постоянное значение. Вопрос сводится к отысканию ф-ии<р(а;, у), которая и определяет по

ур-ию (15) величины напряжений. Функция ·ψ(χ, у) должна удовлетворять ур-иям:

V z=0. V²t®=0, (17)

где у²—диференциальный оператор Лапласа; уравнения (17) после подстановки из (15) перейдут в ур-ие:

S + S= Coast. (18)

Можно доказать, что Const= — 2GT. Решение ур-ия (18) дает распределение напряже-: ний при К. для бруска любой формы, если ф-ия напряжений сохраняет на контуре постоянное значение. Венан применял с большим успехом полуобратный метод для решения этого ур-ия: частью напряжений (де-¹ формаций) он задавался, другие находил по ^; ур-ию (18). Вебер-Риманом дано решение в общей форме логарифмического потенциала. Вебер изучает распределение главного вектора напряжений и таким обр. принимает во ^: внимание влияние нормальных напряжений. Для круга во всех решениях получаются ^; одни и те же ур-ия прочности и деформации. Рейнер рассматривает вал круглого сечения под нагрузкой поверхности, силами и приходит к существенно иной формуле прочности:

<Ю

то есть напряжения в параллельных сечениях ¹ различны. Расчетные зависимости для сече

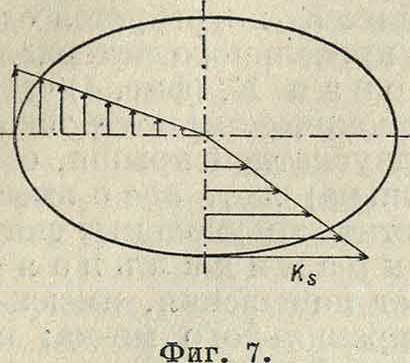
ний (по Венану и частью по Веберу) имеют следующий вид: для эллипса (фигура 7)

2Ms

(20)

где а и Ь—большая и малая нолуоси эллипса,

40 Jo Ms* φ GFi	(21)
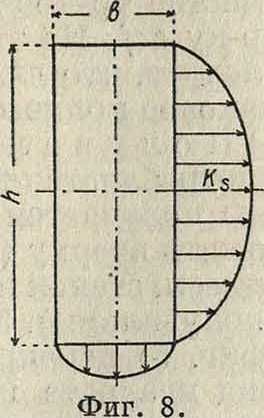
(F—площадь сечения); для прямоугольника (фигура 8)
К- 9 MsS 2 6*/t’	(22)
1,08 40Jo-МУ φ-, ω··< ;.	(23)
Τ. Θ. m. XI.

здесь b и h—стороны, причем b—короткая для равностороннего тр-ка

	Ks =	20 Ms · 6» 9		(24)
здесь	Ь—сторона тр	-ка;
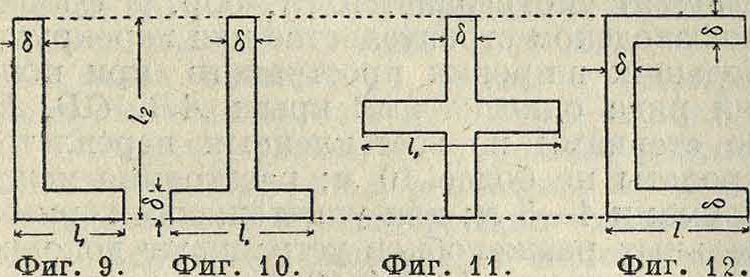
для профилей, показанных			: на фигуре 9—	-14,
	к,	3 MsUS2 ’		(25)
где
	1 — h + ί2""	1,03	(фигура 9),
	1=Ιχ -f- l2 —	1,783	(фигура 10),
	i=ΐχ 4~ ^2—	0,153	(фигура 11),
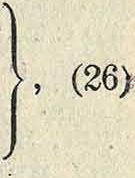
	l=2Ιχ 12 —	2,63	(фигура 12 и	13),
	1=21χ + 12-	1,23	(фигура 14).

Если полки и стенки различной толщины, то тг 3 М е<51 ч

^К*⁼Щ+гЦ (^{для полки})

^к*=Т-_е + гщ (Д^дя стенки)

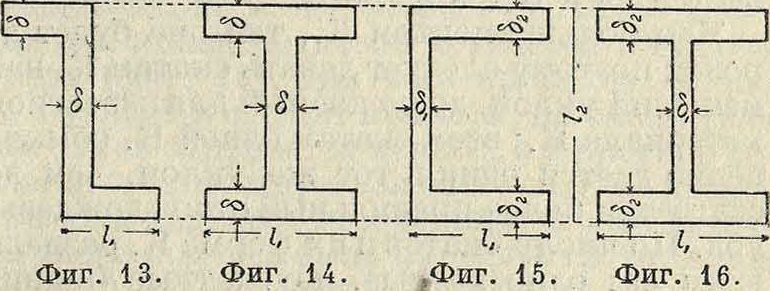
причем для швеллера (фигура 15):

V=21,-6., I"=1,-1,65,; для двухтаврового сечения (фигура 16):

I=21, — 1,26<5₂, I"=1, — 1,67<5₂ + 1,7613!.

Для вала круглого сечения, но с выточкой для шпонки, причем диаметр выточки очень мал, ур-ие прочности:

*.-*£· (27)

напряжение вдвое .больше, чем для полного цилиндра. Для валов с выточкой диаметра d, напряжение равно

di

К,

(28)

Лит.: Тимошенко С. П., Курс сопротивления материалов, 6 изд.,М.—Л., 1928; Б о б а р ы к о в И. И., Сопротивление материалов,.Часть общая, М., 1925; Д и н н и к А. Н., ^Известия Новочеркасск, института», Новочеркасск, 1912; N a v 1 e г, ResumS de leporis etc., P., 1864; Weber, Die Lehre d. Drehfpstigkeit, «Z. d. VDI», 1921; M i s e s R. u. Frank P., Die Differential- u. InU-gralgleiclmngen d. Mechanik u. Physik, 7 Aufl., В. 1—2, Brscliw., 1925—27; F i 1 ο n G., «Philosophical Transactions of the Royal Society of London», London, 1900, v. 193, series A. p. 309; В a c h С. u. В a u m a η n R., Elastizitat u. Festigkeit, 9 Aufl., B., 1924. С. Лебедев.