 > Техника, страница 58 > Линии влияния
> Техника, страница 58 > Линии влияния
Линии влияния
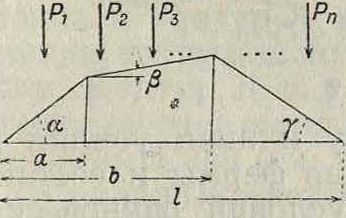
Линии влияния, инфлюентные линии, представляют собой графич. изображение закона изменения усилия или момента в сечении или точке сооружения в зависимости от груза, равного единице, перемещаемого но грузовой линии сооружения. Л. в. может изображать также закон изменения деформации в сечении и линейного смещения точки сооружения в зависимости от перемещения груза, равного 1, по сооружению. Каждая ордината у Л. в (фигура 1), взя
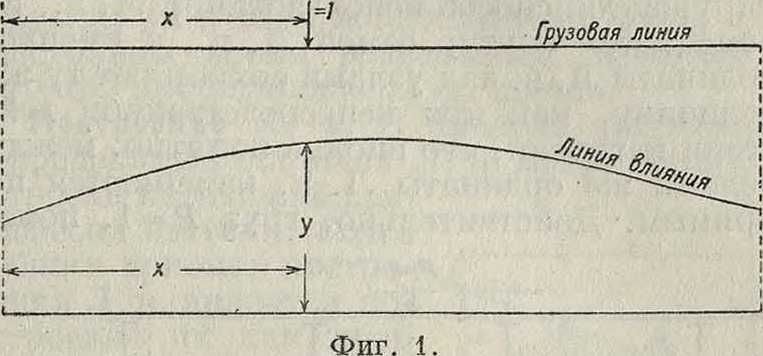
тая под положением груза, равного 1, определяет собой, смотря по назначению Л. в., величину усилия, момента или деформации в сечении или точке сооружения, для которого она построена. Ординаты Л. в имеют различную размерность, что зависит от ее назначения; если Л. в определяет закон изменения момента, то ординаты ее имеют измерение в см; если она определяет усилие, то ординаты ее—отвлеченное число; если она определяет линейное перемещение, то ординаты ее—см/кг; если она определяет угловую деформацию, то ординаты ее —
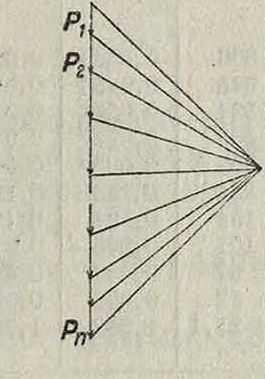
Свойства Л. в позволяют находить наиневыгоднейшее положение подвижной нагрузки для рассматриваемого усилия, момента, деформации и т. д., что очень важно для расчета сооружений, подвергающихся действию подвижной нагрузки, могущей занимать любое положение на сооружении. Вместе с тем Л. в на основании закона независимости действия дают возможность определять величину усилия, момента, деформации и прочие от воздействия ряда нагрузок или системы их как сумму воздействий отдельных грузов. Если это будет ряд сосредоточенных грузов Рц Р2,.,Рк, то величина усилия S, для которого построена Л. в., определяется выражением
k
S=Ρι2/ι + Ρ2ί/2 + + Ркук=^Ру.
i
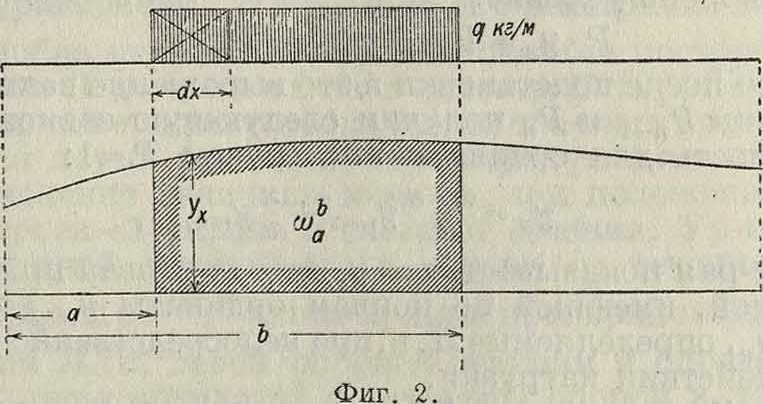
Если сооружение загружается равномерно распределенной сплошной нагрузкой q кг/м, расположенной на участке с абсциссами а и Ь (фигура 2), то величина усилия S определится по Л. в выражением ь ь
S^^yxq dx= q^yxdx= q wba, a a
где (oba—площадь Л. в на участке между абсциссами а и b. Если нагрузка передается
*4
на сооружение не непосредственно, как было указано в двух предыдущих случаях, а при посредстве балочек (фигура 3), передающих нагрузку в определенные точки сооружения, называемые узлами, то этим не нарушается способ использования Л. в., но изменяется контур самой Л. в., а именно: ординаты Л. в над узлами сохраняют ту же величину, как при непосредственном действии нагрузки, что вполне понятно, между узлами же ординаты Л. в изменяются по прямым. Действительно, груз Р= 1, поме
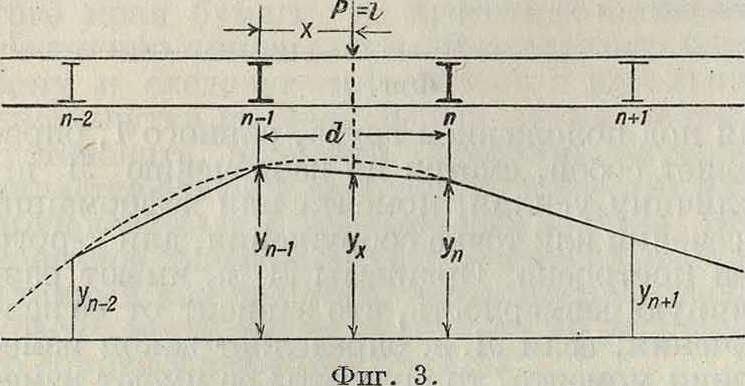
щаясь между узлами (фигура 3), разлагается на два:
т. к. по свойству Л. в должно быть удовлетворено условие:
Р Ух = -^п—1 Уп—1 “Ь -Рп ’ Уп, топосле подстановки в это выражение величин Р„_! и Рп получим следующую зависимость для ординаты под грузом Р=1:
d - х -, х Ух Уп—1 ^ Уп ϊ
к-рая показывает, что ух есть ордината прямой, имеющей по концам ординаты уп^ и уп, определяемые Л. в.при непосредственном действии нагрузки.
Использование Л. в заключается в двух операциях: определении невыгоднейшего положения системы грузов на сооружении и определении наибольшего усилия для выбранного расположения.
1) Определение невыгоднейше-гоположениясистемы грузов на сооружении. Если расстояния между грузами системы остаются постоянными, то величина суммарного воздействия Z есть ф-ия одного переменного х—расстояния первого груза от левой опоры: Z(x)=VPy. Наибольшее значение этой ф-ии мы найдем, приравнивая нулю ее производную по х:
Z(x)=^Ptg<p=Q, (1)
где через φ обозначен угол наклона любой ветви к горизонту. Т. к. грузы Р имеют обычно одинаковый знак, то знак каждого члена суммы определяется знаком тангенса и равенство м. б. написано в виде:
2 (рлее. tg φ)=2 (рправ. tg ψ), (3)
причем к левым грузам относятся те, которые расположены на восходящей части Л. в., а к правым—расположенные на нисходящей. Очевидно сумма ΣΡ tg<p может менять величину только при переходе какого-либо груза через одну из вершин; поэтому максимум Z может иметь место только п р и у с т а-новке одного из грузов, называе мого при этом критическим, над одной из вершин. Это свойство Л. в весьма упрощает задачу нахождения максимума Z, сводя решение к конечному и небольшому числу пробных установок. Из определения критич. груза следует, что при переходе его через одну вершину Л. в сумма (1) меняет знак, а левая часть равенства (2) становится больше правой, если до перехода она была меньше ее, и обратно. Поэтому окончательным критерием для нахождения невыгоднейшего положения нагрузки оказывается следующее правило: если при отнесении предлагаемого критического груза к левым грузам имеем
^ J (Рлев. * tg ψ) + Ркрит. * tg Ψ -:> 21 (Рправ * tg Ψ) >
а при отнесении его к правым грузам имеем
2 (-Рлее. - tg Ч>Н 2 (Рправ Λg ψ) “Ь -Ркрит. •tg ψ,
то соответственный груз является критическим и невыгоднейшее загружение найдено. В частности для треугольной Л. в это правило принимает такие формы:
Σρ*
;т2р>
2 Рлев где в правых частях стоят суммы всех гру^ зов, а—длина левой ветви Л. в В криволинейных Л. в определение невыгоднейшего загружения проще всего вести графич. путем, вычертив Л. в на миллиметровой бумаге; передвигая по Л. в полоску бумаги с отмеченными на ней взаимными положениями грузов и изменяя ординаты под грузами, можно быстро найти максимум после 2—3 пробных установок. Если кривая Л. в очерчена по параболе или близкой к ней кривой, невыгоднейшее положение системы имеет место при совпадении равнодействующей системы с вершиной параболы.
2) Вычисление усилий и моментов по Л. в для данной нагрузки. После того как найдено невыгоднейшее положение системы на Л. в., целесообразно вычисление усилия или момента производить следующ. способами. Если Л. в имеет форму треугольника и загружена сосредоточенными грузами ΡνР2,., то, обозначив углы наклона линии влияния к горизонту через а и β (фигура 4), имеем:
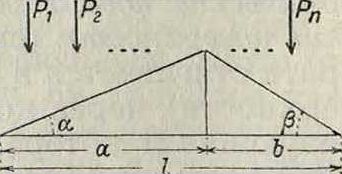
Фигура 4.
Z=2-Pi=tg а^ Рж + tg ^2]ρ(1~χ),
где первая сумма распространяется на грузы, стоящие над левой ветвью Л. в., а вторая на грузы над правой ветвью. Обе суммы выражают статич. моменты грузов относительно левой и правой опоры соответственно. Выражение это можно преобразовать:
Z=tg β^Ρ(1-χ)-^α + tg β)νίΡ(α-χ),
где первая сумма распространяется уже на все грузы, стоящие на сооружении, а вторая—на грузы, стоящие над левой ветвью Л. в Это выражение удобно в том отношении, что обе суммы представляют статич. моменты левых грузов относительно правой опоры и одновременно вершины Л. в.; вполне понятно, что аналогичное преобразование формулы м. б. сделано также для правой ветви Л. в При таком преобразовании значительно облегчается расчет усилия путем составления таблиц моментов грузов от первого до п-то для данной системы по следующей схеме:
Момент гру-
п
ЗОВ Σμ 1
относительно груза η
Такие таблицы составлены для всех расчетных схем нсел.-дор. поездов и частично для нагрузок шоссейных мостов. Наличие 3-й графы позволяет легко вычислить момент левых грузов относительно любой промежуточной точки; так, момент относительно точки, отстоящей от и-го груза на с [в сторону (п+1)-го], определяется из
П
М - Мп + с 2 р.
1
Если Л. в имеет многоугольное очертание, то воздействие системы грузов выражается аналогичным образом (фигура 5):
Ζ — tg γ 2 P(l - ж) - (tg У + tg /3)2Р(Ь-ж)-
— (tg α — tg /?) 2 Ρ(α — x)>
где первая сумма—момент всех грузов относительно правой опоры, вторая—всех левых грузов относительно вершины b, третья— всех левых грузов относительно вершины а и т. д. Таблицы моментов сохраняют применимость и в самом общем случае.
Фигура 5. Фигура 6.
3) Расчет по эквивалентным нагрузкам. Для упрощения расчета по Л. в можно пользоваться эквивалентной нагрузкой, то есть такой сплошной равномерной нагрузкой р, воздействие которой на сооружение равно воздействию от данной системы сосредоточенных сил. Если ω—площадь Л. в., то эквивалентная нагрузка определяется из условия
Z=^Py=pa>,
откуда p=f.
Удобство расчета заключается в том, что воздействие системы грузов может быть найдено путем простого умножения соответствующей эквивалентной нагрузки на площадь Л. в Кроме того величины эквивалентных нагрузок дают удобный способ сравнения интенсивности загружения, производимого различными системами грузов. Пользование эквивалентными нагрузками облегчается наличием таблиц, составленных для всех расчетных и большинства существующих ж.-д. поездов, для различных пролетов мостов и для различных типов Л. в (обычно для Л. в момента в середине и четверти пролета и для Л. в поперечной силы у опор и в

№ груза
Длина от 1-го груза до груза п
Сумма гру-п зов Ϊ.Ρ
Фигура 7.
четверти пролета). Эквивалентные нагрузки для Л. в промежуточных точках находятся линейной интерполяцией. Расчет по эквивалентной нагрузке значительно проще, чем расчет по системе грузов, так как не требует нахождения невыгоднейшего положения нагрузки; он к тому же достаточно точен, и в настоящее время разрешается применять его при проектировке ж.-д. мостов.
Построение Л. в В простых статически определимых системах Л. в могут быть построены из условий равновесия статики; более общим приемом построения Л. в является построение их как эпюр возможных перемещений, что позволяет проводить построение их как в системах статически определимых всякого вида, так и в системах статически неопределимых.
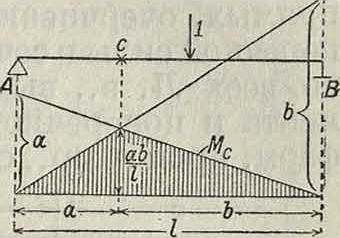
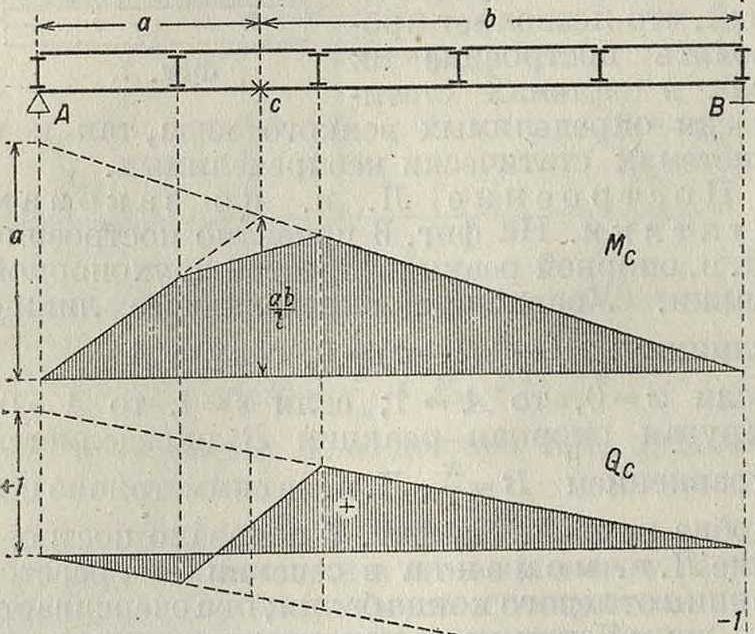
Построение Л. в по законам статики. На фигуре 6 показано построение Л. в опорной реакции простой двухопорной балки. Уравнение, определяющее линию влияния: А1 — 1 (I — ж)=0, откуда А=* 1~ если х=0, то А=1; если х=Ϊ, то А=0. Другая опорная реакция В определяется уравнением В=“, Л. в ее симметрично подобна первой. На фигуре 7 показано построение Л.в. момента в сечении С на расстоянии а от левого конца балки; она очерчивается двумя прямыми, характеризующими изменение величины момента при положении грузα= 1 справа и слева от сечения. Ур-ие правой прямой (груз справа от сечения)
Мс=Аα= - - а; эта прямая пропорциональна Л. в левой опорной реакции и определяется ординатой а под левой опорой и нулем под правой опорой. Ур-ие левой прямой (груз слева от сечения) МС==ВЬ=“ 6; эта прямая пропорциональна правой опорной реакции и определяется ординатой b под правой опорой и нулем под левой опорой. .Обе прямые пересекаются на вертикали под точкой момента.Это свойство позволяет ограничиться при построении Л. в моментов ур-ием одной прямой, т. к. вторая прямая будет определяться нулевой точкой под опорой и точкой пересечения первой прямой с
+? !
я-г—
Фигура 8.
~1-в

if —ii
вертикалью под сечением. Наибольшая ордината Л. в момента под точкой сечения равна-^. На фигуре 8 показано построение Л. в. поперечной силы. Эта Л. в очерчивается двумя прямыми. Ур-ие правой пря-
мой (при положении груза равного 1 справа от сечения) Q=А=; это та же прямая,
которой очерчивается Л. в левой опорной .реакции. Ур-ие левой прямой (при положении груза равного 1 слева от сечения) Q=— в=— эта прямая пропорциональна Л. в правой реакции, но с обратным знаком. Обе прямые параллельны между собой; распространение их ограничивается вертикалью под сечением. Указанные свойства прямых, очерчивающих Л. в момента и поперечной силы в сечении балки, сохраняются во всех Л. в., выражающихся в ф-ии момента и поперечной силы, например в Л. в ферм, арок и прочие, о чем смотрите ниже. На фигуре 9
Фигура 9· ~ __!
показано построение Л. в сечении С балки при передаточном действии нагрузки. Они очерчиваются каждая теми же прямыми, как при непосредственном действии нагрузки, но в пределах между узлами, между к-рыми лежит сечение, контур Л. в изменяется и она имеет очертание по прямой между ближайшими узлами. Изложенные основные положения о построении Л. в двух опорных балках сохраняются в силе и для других видов балок. При наличии в балках промежуточных шарниров (фигура 10), характери-
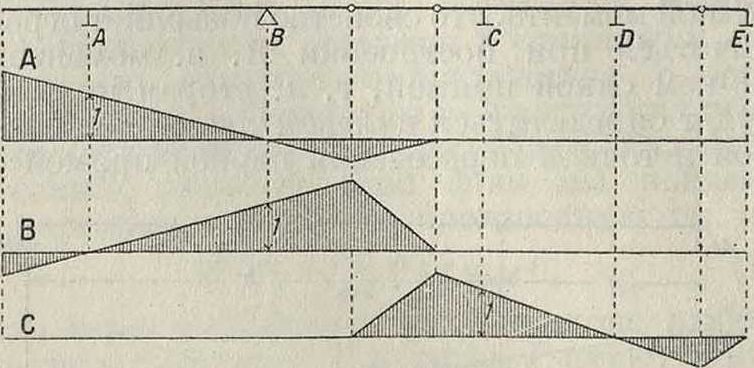
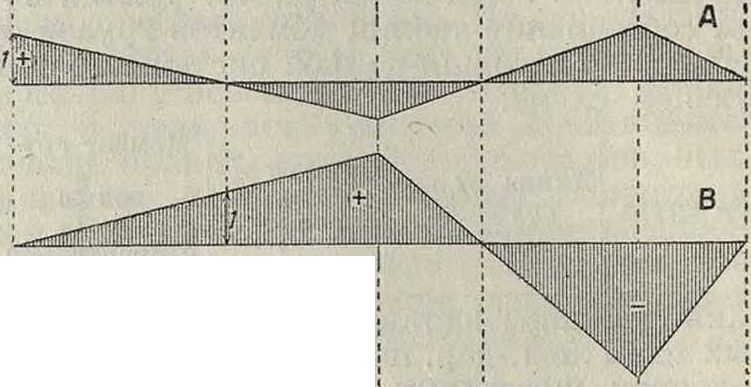
Фигура ю. зугощих собой передачу на балки нагрузки через шарниры, Л. в между шарнирами изменяется по прямым, как для узловой нагрузки. На фигуре 10 показано построение Л. в опорных реакций А, В и С для консольной балки с подвесными бал очками. Если между опорами балки помещается один шарнир (фигура 11), то Л. в изменяется по прямой между этим шарниром и ближайшей опорой, от которой проходит по прямой до следующего шарнира и т. д. Так как Л. в сечениях балки пропорциональны Л. в опорных реакций, то прямые, очерчивающие Л. в мо
Фигура ii-
мента и поперечной силы в балках с промежуточными шарнирами, должны распространяться до шарниров, а между шарнирами должны изменяться по прямым (фигура 12), как это было показано для Л. в опорных реакций таких балок (смотрите Балки простые). Л. в усилий в фермах определяются из уравнений,
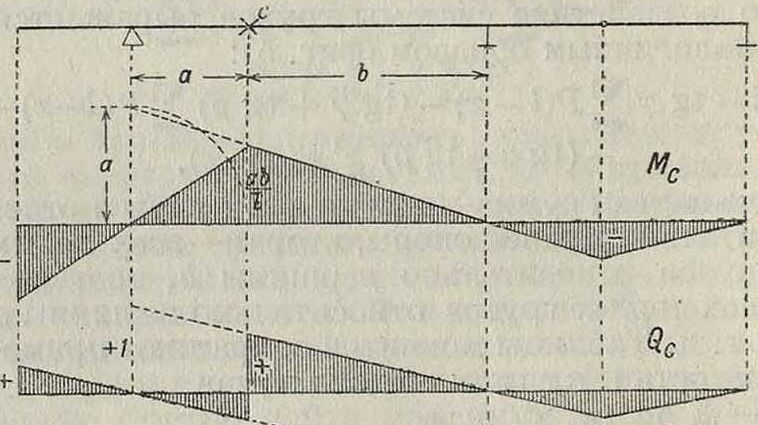

Фигура 12.
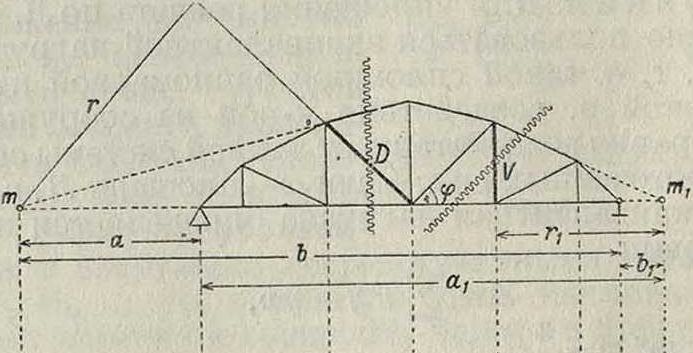
определяющих величину и знак усилия в рассматриваемом стержне фермы и составляемых на основании условий равновесия или относительно точки момента (точка Риттера) или из условия проекций (смотрите Фермы).
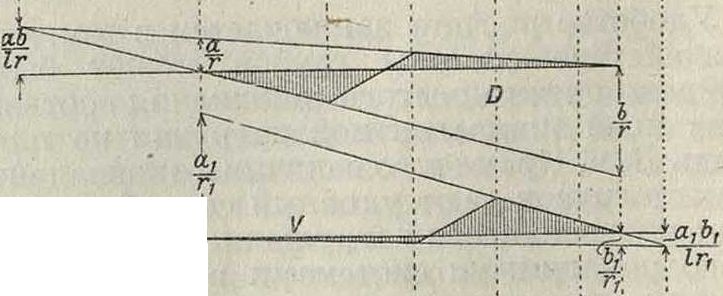
Нагрузка [ понизу
Нагрузка;поверху L
Фигура 13.
Но и в этих Л. в сохраняются указанные выше основные свойства их. Так, Л. в раскоса D фермы, показанной на фигуре 13, опре деляется из ур-ий равновесия относительно точки схода т рассеченных стержней верхнего и нижнего поясов; условия равновесия будут: правой прямой, при положении груза равного 1 справа от сечения,
Вг - Аα= 0; D= + i “=Ц- а;
левой прямой, при положении груза равного 1 слева от сечения,
— Вг — Вb=0; В=-Въ=~уЬ
Построение этих прямых дано на фигуре 13, из которой видно, что они пересекаются на вертикали под точкой моментов; распространение их ограничивается грузовыми узлами, ближайшими к сечению, между которыми Л. в изменяется по прямой. На той я-te фигуре показано построение Л. в для стойки V. Ур-ие усилия этой стойки определяется относительно точки моментов т1 и будет: при положении груза справа от сечения
— Угг + Аах=0; V=+ А ^ ~
чем определяется ордината равная +~ правой прямой под левой опорой; левая прямая определяется точкой пересечения правой прямой с вертикалью под точкой моментов и нулевой точкой под левой опорой. В тех случаях когда сечение, проводимое для определения усилия в стойке, рассекает элементы верхнего и нижнего пояса между узлами, не лежащими на одной вертикали, контур Л. в меняется в зависимости от того, где проходит грузовая линия—по нижним или верхним узлам. Сопоставление контуров Л. в для этих двух случаев сделано на фигуре 13, где показан контур Л. в стойки V при расположении нагрузки по верхним и нижним узлам. Контур Л. в фермах существенно зависит от очертания поясов фермы и системы решетки в ней (смотрите Фермы).
В сложных системах Л. в определяются ур-иями, состоящими из суммы членов, что заставляет прибегать к суммированию отдельных прямых, характеризующих влияние отдельных членов уравнения; типичными примерами такого суммирования служат Л. в системах с распором (арки, комбинированные висячие системы и прочие). Ток, Л. в арках являются результатом сложения видоизмененных Л. в вертикальной реакции V и распора II. Например Л. в момента в любом сечении арки определяется ур-ием: при положении груза равного 1 справа от сечения (фигура 14)
Мс=VAac- Нус.
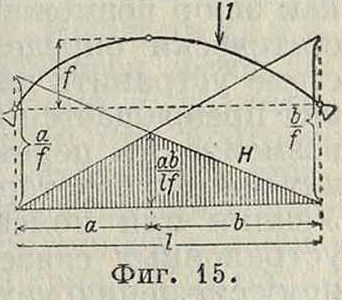
Входящий в это выражение первый член аналогичен ур-ию Л. в простой двухопорной балке и следовательно Л. в., его очерчивающая, имеет форму тр-ка с вершиной под сечением. Что касается второго члена, то он зависит от Л. в распора II. Величина самого распора Я определяется из выражения момента для промежуточного шарнира S, для которого (фигура 15)
Ms=Vаа — Я=0, откуда Я=~^·
Следовательно Л. в распора подобна Л. в момента в шарнире S и имеет форму тр-ка с вершиной под шарниром и наибольшей ординатой под ним а^. На фигуре 14 контур Л. в второго члена— Нус очерчен тр-ком aSb с ординатой η у, над правой опорой. Путем сложения ординат указанных двух членов определяется суммарная Л. в момента
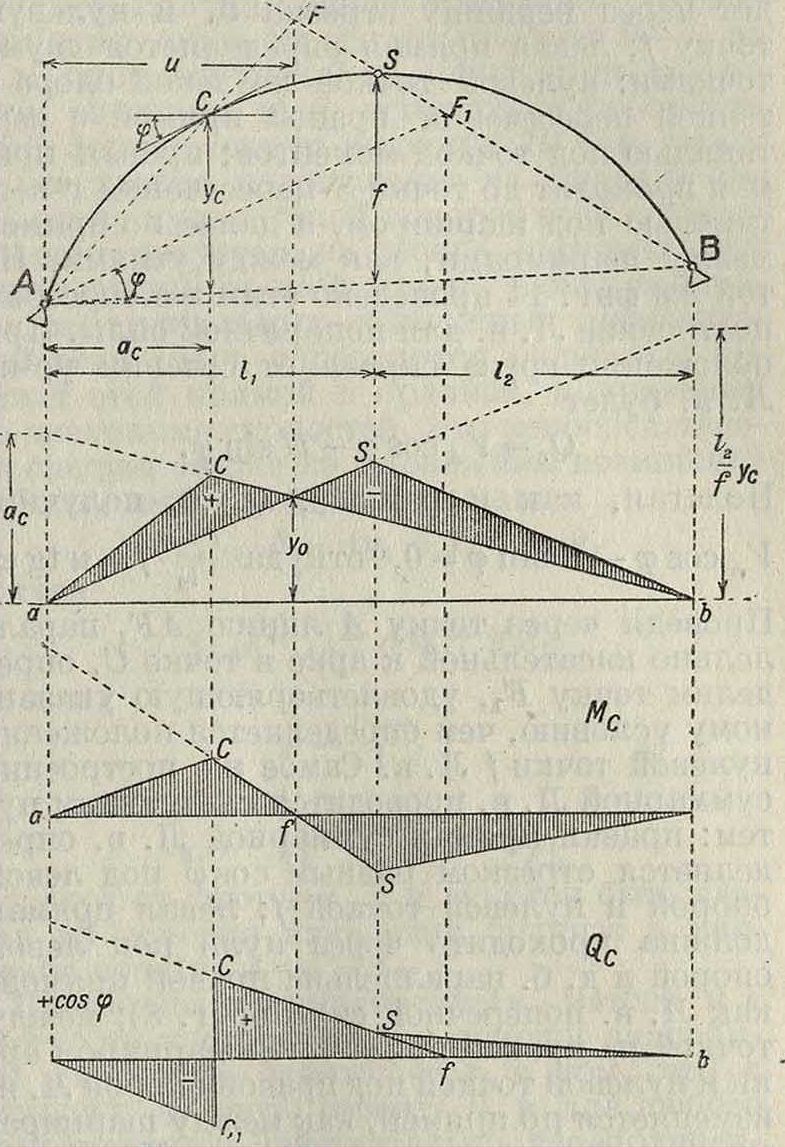
Фигура 14.
в сечении С. Однако целесообразнее такие Л. в строить по нулевым точкам. Из фигура 14 видно, что нулевая точка Л. в., удовлетворяющая условию Мс=VAac — Нус=0, находится на пересечении правой прямой Л. в VAae и левой прямой Л. в Нус.
Если предположить, что эта точка находится на некотором расстоянии и от левой опоры, то при положении груза равного 1 на этой точке, что соответствует условию М„=0, величина
7_эд опорного давления VA=— - и величина рас-
LL I
пора Я=г у. Подставив эти и Я в вышеприведенное получим:
I — и и U π I — и» Ус .,
ас - j ус=0, откуда, -=~ и. значения VАусловие Мс=0,
1
ia
ас
Это отношение позволяет определить положение нулевой точки следующим простым геометрич. построением на самой арке. Прямыми SB и АВ определяются вертикальные отрезки, удовлетворяющие условию [-(I — м)
при любом и; прямыми АС и АВ определяются вертикальные отрезки, удовлетворяю щие условию - и при любом и; очевидно,
а С
что равенству этих отношений удовлетворяет отрезок, засекаемый прямыми BS и АС. Зная точку F и положение ее на оси абсцисс, можно построить Л. в без суммирования, а именно: при суммировании отрезок ас правой прямой Vа сохраняет свою величину, поэтому эта прямая в суммарной Л. в пройдет через вершину отрезка ас и нулевую точку /; левая прямая определяется двумя точками: нулевой точкой на левой опоре и точкой пересечения правой прямой с вертикалью под точкой моментов; правая прямая проходит до точки S пересечения с вертикалью под шарниром, а далее по прямой между шарнирами, как между узлами. На той же фигура 14 проведено этим же способом построение Л. в для поперечной силы. При положении груза справа от сечения ур-ие Л. в будет
Qe=E^COS φ —Н sin φ.
Полагая, как и раньше, ζ>0=0, получим:
I ~~ ZL
V А cos φ — Н sin φ=0, откуда ^=wtg<p.
Проведя через точку А линию AF3 параллельно касательной к арке в точке С, определим точку /<’, удовлетворяющую указанному условию, чем определяется положение нулевой точки Л. в Самое же построение суммарной Л. в проводится следующим путем: правая прямая суммарной Л. в определяется отрезком равным cos φ под левой опорой и нулевой точкой /; левая прямая должна проходить через нуль под левой опорой и должен быть параллельна правой прямой, как Л. в поперечной силы (фигура 8); между точкой на правой прямой под шарниром арки и нулевой точкой под правой опорой Л. в изменяется по прямой, как между шарнирами. Такой прием суммирования Л. в распространяется на все статически определимые системы с распором (смотрите Фермы).
Построение Л. в по законам кинематики. Более общим приемом построения Л. в является рассмотрение их как эпюр возможных перемещений. Если в статически определимой неизменяемой системе устранить какую-либо связь, то этим она превращается в механизм, получающий возможность перемещения, к-рое происходит вокруг некоторых мгновенных полюсов. Усилия или момент, приложенные взамен устраненных связей, препятствуют свободному смещению механизма и удерживают его в равновесии. Если рассматривать такой механизм под действием груза равного 1 и обозначить величину устраненной связи через S, то равновесие системы, по условию равенства нулю работы, определится ур-ием:
- SS[+ 1 · у=0, откуда S=|,
где <5—перемещение, возможное по направлению устраненной связи; у—перемещение, возможное по направлению груза равного 1. Если определить величины у возможных перемещений всех точек грузовой линии, то этим определится эпюра возможных перемещений ее. Из полученного выражения усилия устраненной связи непосредственно видно, что если измерить ординаты эпюры возможных перемещений грузовой линии в мас
штабе <5=1, то она представит собой Л. в устраненной связи. Эпюра возможных перемещений является как бы моделью Л. в Таким образом вопрос сводится к построению эпюры возможных перемещений грузовой линии и определению величины д возможного перемещения по направлению устраненной связи, к-рое должно служить единицей масштаба. Построение эпюр возможных перемещений в статически определимых системах облегчается тем, что каждое жесткое звено, входящее в состав системы, имеет возможную подвижность, вращаясь только вокруг мгновенного полюса; эпюра возможных перемещений в этом случае характеризуется прямой, имеющей нуль в проекции точки неподвижного полюса. Например если в балке, лежащей на 2 опорах, в каком-либо „м<и сечении поместить шар-
АС с 1В нир (фигура 16), то бал ка представится в виде механизма, могущего вращаться вокруг ука-Фигура 16. занного шарнира, при чем возможная для нее эпюра перемещений характеризуется двумя прямыми с нулевыми точками под абсолютно неподвижными полюсами Ли В и пересекающимися между собой под относительным полюсом (смотрите Механика теоретическая). Балка будет удерживаться в равновесии моментами Ж, приложенными в шарнире; ур-ие работы для этого случая выразится в таком виде:
-МЛа+19) + 1-»-0, откуда Жс=-!^/3;
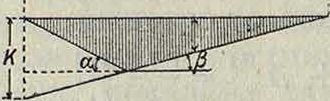
величина (α + β) определяется отношением к : а; если отрезок к будет равен а, то ур-ие приводится к виду Мс=у, то есть эпюра перемещений представит собой непосредственно Л. в момента, что и будет соответствовать действительности, т. к. каждая ордината ее у будет равняться а—, что определяет собой величину момента. На фигуре 17 постро-
д
1s
ДЛЗаашжв.
-"wnasSf
Фигура 17.
ена эпюра возможно-го перемещения балки, если у нее в том же сечении будет устранена связь, препятствую-щая поперечному сдвигу. Ур-ие возможной работы в этом случае выразится так:
у _ у I
— Q (с + e) + 1 · у=0, откуда Q =
С + С δ rj
Приняв (с+с)= 1, получим масштаб, при к-ром ординаты эпюры перемещений будут представлять собой Л. в поперечной силы. Выразив ординату у через отрезок <5=с+с,
а именно: у=(с+с) - у-, полущим Q=; х что соответствует уравнению Л. в поперечной силы.
На фигуре 18 показано применение этого способа построения Л. в для усилий в стержнях простых ферм. Устранение раскоса фермы дает возможность смещения обеим частям ее путем вращения вокруг абсолютных полюсов 4иВ. Эпюра возможных перемещений характеризуется двумя прямыми, пересекаемыми третьей прямой в проекциях под относительными полюсами 3, 5 и 4, 6. Выражение возможной работы в этом слу-
чае будет: при положении груза равного 1 в правой части
— Ώδ + 1 · у=0, откуда Ώ=+1;
при положении грузα= 1 в левой части
— Ώδ — 1 у=0, откуда Б=— ^,
где <5—суммарное перемещение по направлению усилия Б. Разница в знаках показы
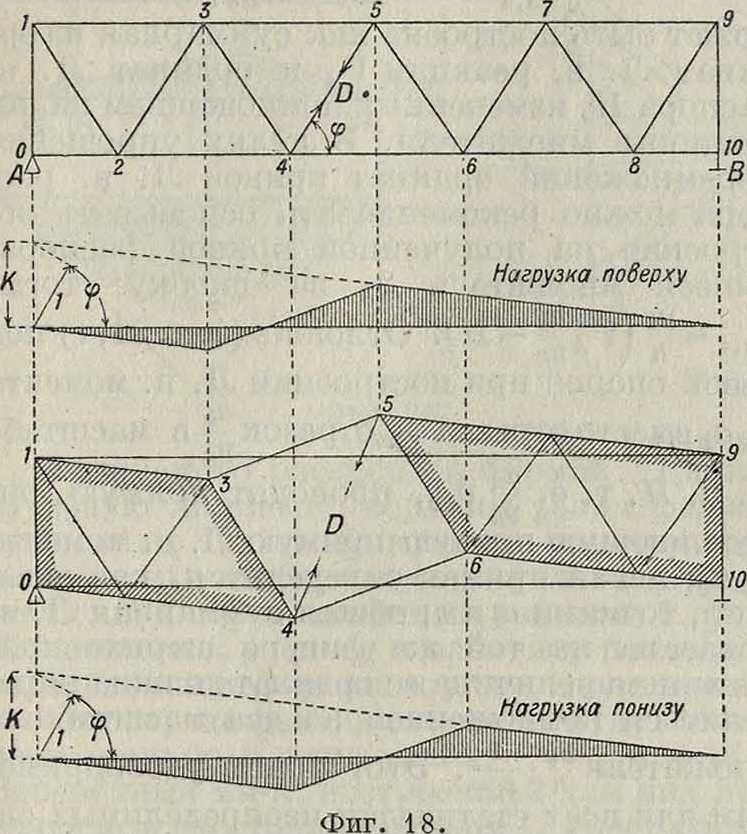
вает, что усилие раскоса имеет разные знаки взависимости от положения нагрузки, как это и надо было ожидать (смотрите Фермы). Т. к. в данном случае точка моментов лежит в бесконечности, то относительное смещение обоих звеньев определяется отрезком к, величина же возможной деформации раскоса δ=к sin <р, что непосредственно видно по проекции полного перемещения к на направление раскоса.
В фермах со сложной решеткой, когда система превращается в механизм с целым рядом звеньев, целесообразно производить построение эпюры перемещений при помощи
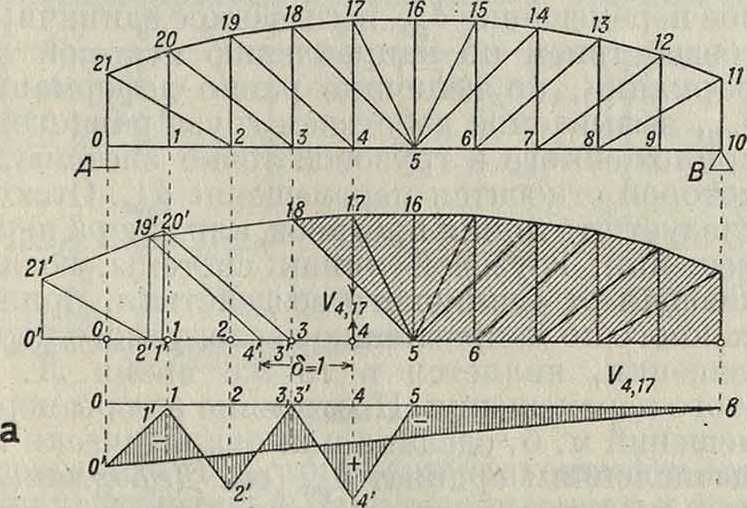
Фигура 19.
диаграммы или эпюры скоростей (смотрите Кинематический метод). На фигуре 19 показано построение диаграммы скоростей в двураскос-иой ферме при устранении из нее” стержня стойки via7, а по ней эпюры возможных перемещений’для узлов нижнего пояса. При устранении стойки v4:17 узел 4 фермы получает возможность вертикального смеще ния с некоторой скоростью 4—4, определяемой изображающей точкой 4 (смотрите Кинематический метод). По этой точке 4 строятся последовательно изображающие точки 3, 19, 20, 2, 1, 21 и 0, определяющие скорости в узлах 3—3, 2—2, 1—1 и 0—О. Отложив эти отрезки в виде ординат от оси абсцисс, получим эпюру возможного смещения этих узлов относительно звена 0—5, но т. к. опорный узел 0 не может иметь смещения, то эпюра должен быть исправлена поворотом всей фермы вокруг шарнира 10 так, чтобы в результате перемещение на опоре 0 было равно нулю; такой поворот всей системы охарактеризуется на эпюре вертикальных перемещений прямой 10—0. Тогда величины действительных возможных перемещений всех узлов определятся разностью ординат этой прямой и ординат, полученных по диаграмме скоростей. Это непосредственно следует также из выражения возможной работы, к-рое изобразится так:
- ^4,17 -δ-Ay о +1 · 2/,р=О,
откуда
vM7=^[-^2/o + ypi,
но т. к.
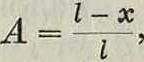
то
i г i - х, i Vi,n — и У О + Vpj
Переход от эпюры к Л. в должен быть сделан из условия измерения ординат в масштабе отрезка 4—4= <5=1.
Преимущество кинема.тическ. метода и в частности построения при помощи диаграммы скоростей заключается в том, что с помощью ее легко строить Л. в для любого направления. Действительно все полученные по фигура 19 отрезки скоростей были отложены нами по вертикальному направлению в полном виде, но они могли быть отложены по любому направлению в виде отрезков, равных проекции этих скоростей на новое направление.
Л. в статически неопределимых системах. Кинематическ. метод лежит также в основе построения Л. в статически неопределимых систем; при построении Л. в этих системах устраняется лишняя связь и изучаются перемещения грузовых точек системы, становящиеся возможными при устранении этой связи. При наличии в системе одной неизвестной×величина ее определяется выражением×= — (см.
°хх
Статически неопределимые системы), которое при действии на систему груза равного 1 приводится к виду·
__ dg;l __ δ1χ
δχχ &ΧΧ.
так как на основании теоремы о взаимности перемещений δχΧ=δ1χ. В этом выражении числитель δ1χ представляет собой линейное перемещение по направлению груза равного 1, вызываемое единичным воздействием по направлению устраненной связи, а знаменатель представляет собой деформацию угловую или линейную по направлению самого неизвестного от того же единичного воздействия Х=1. Т. о., если будут известны перемещения всех грузовых точек системы, вызываемые воздействием Х=1, то есть будет найдена эпюра возможных перемещений, то при измерении ординат эпюры в масштабе <5га=1 получим Л. в неизвестного. Построение эпюр перемещений целесообразнее делать графически при помощи упругих грузов, определяемых как угловые деформации: в сплошных системах из выражения м,
g^as, а в сочлененных системах как угловые деформации шарнирной цепи (смотрите Графическое определение перемещений). На фигуре 20 показано построение Л. в двупролетной балке, с рассмотрением в ней, в качестве лишнего неизвестного, момента на средней опоре. Эпюра перемещений будет иметь вид двух кривых, показанных на чертенке; она представляет собой модель Л. в.; переход к Л. в должен быть сделан путем установления масштаба δχχ=1. В данном случае деформация дхх представляет собой угловую деформацию, определяемую тангенсом угла между касательными к обеим ветвям эпюры в точке приложения неизвестного момента. На фигуре 20 показано построение Л. в той же балке, но при условии рассмотрения в ней, в качестве лишнего неизвестного, опорной реакции А. Эпюра перемещений, становящаяся возможной в системе при устранении этой реакции, показана на том же рисунке; она при-водитсякЛ.в.этой реакции при измерении ее ординат в масштабе ^жж=?/о=1· На фигуре 21 показано построение Л. в для двухшарнирной арки, в которой за неизвестное принят распор Я. Эпюра перемещений, построенная по упругим грузам, определенным по угловым деформациям в шарнирной цепи, вызываемым воздействием ж(Я)=1, имеет вид кривой (фигура 21,6). В
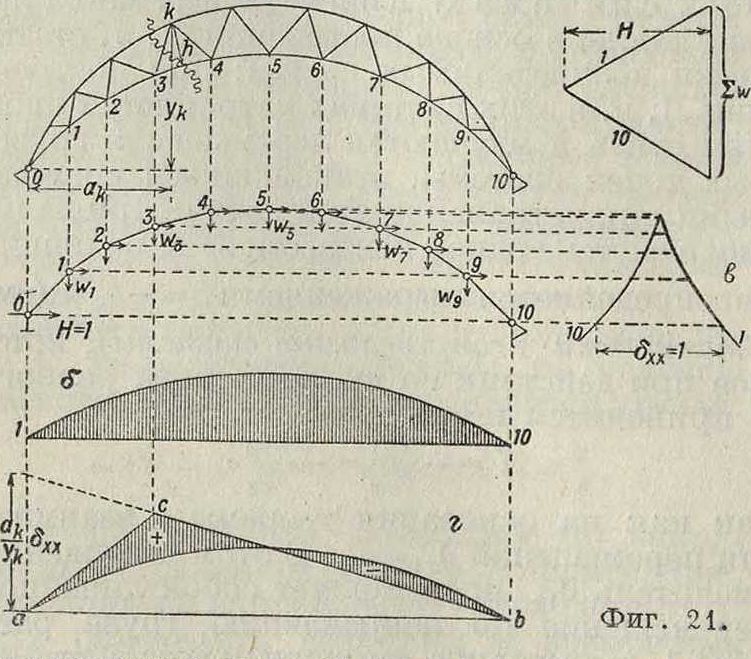
рассматриваемом случае определение масштабного множителя <5ет=1 должен быть сделано или аналитич. расчетом по формуле δχχ=V N&s
(смотрите Деформация) или графич. построением эпюры перемещений для горизонтального направления, как это показано на той же фигура 21, в Построение Л. в внутренних усилий статически неопределимых систем после определения в ней Л i в лишних неизвестных сводится к построению суммарных Л. в по соответствующим ур-иям. Так например Л. в поясного стержня той же арки, определяемая ур-ием вида
VAak-Hyk,
может быть построена как суммарная из ординат Л. в реакции Vл и ординат Л. в распора Я, измененных помножением на постоянные множители. В целях упрощения перемножений ординат кривой Л. в распора можно рекомендовать основывать построение на полученной кривой распора, вынеся множитель ук за скобку; тогда
w3,4=)f Отложив (фигура 21,г) под левой опорой при построении Л. в момента VАак вместо отрезка ак отрезок ~ в масштабе
Л. в Я, то есть “* дхх, проводят прямую, определяющую правую прямую Л. в момента Vлак левая прямая определится, как известно, точками а и с; общая суммарная Л. в показана на той же фигуре штриховкой. Истинная величина ее ординат должна определиться помножением на два масштабных множителя Этот прием удобоприме-
ним для всех статически неопределимых систем с одним неизвестным. При наличии в системе нескольких неизвестных вопрос с построением Л. в осложняется, но в нем могут быть достигнуты упрощения специальными преобразованиями (смотрите Статически неопределимые системы). Для построения Л. в нек-рых общеупотребительных статически неопределимых системах существуют специальные таблицы: например для расчета неразрезных балок—таблицы Griot; для расчета сводов, заделанных пятами,—таблица Strassner’a и др.
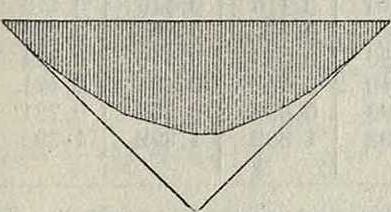
Л. в деформаций. По теореме о взаимности перемещений всякое перемещение вида дар=дра, из чего следует, что линейное перемещение δρα, вызываемое единичным воздействием по направлению искомой деформации, по величине равно деформации δир, вызываемой действием груза равного 1, приложенного в грузовой точке системы, к которой относится перемещение δρα. Отсюда следует,что линия прогибов, или эпюра перемещений, грузовой линии системы, возникающая от единичного воздействия, приложенного по направлению исследуемого перемещения, является в то же время Л. в этого перемещения. Построение эпюры перемещений м. б. сделано или аналитически по вычислениям ординат δρα (смотрите Деформация) или графически при помощи упругих грузов (смотрите Графическое определение перемещений). Ординаты этих эпюр, измеренные в масштабе, соответствующем полюсному расстоянию равному 1, определяют собой Л. в изучаемой деформации. В системах со сплошными сечениями, где условия деформации в каждом сечении определяются выражением вида И7=ds, построение эпюры перемеще-I ний, а следовательно Л. в., делается какве-
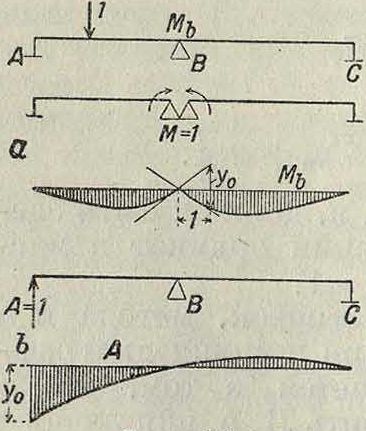
Фигура го. ревочного мн-ка для фиктивного загруже-ния системы эпюрой моментов при полюсном расстоянии, равном 1 (фигура 22). На фигуре 23 показано построение Л. в деформации угла
Л 1
^Трг г 11 I;
Фигура 22.
а, образуемого раскосом и фермой. Приняв грузовую линию по верхним узлам фермы, вычисляют для нее фиктивные упругие грузы (угловые деформации в углах) от действия двух пар с моментами равными 1, приложенными к раскосу и элементу пояса для определения деформации угла. В рассматриваемом случае фиктивные грузы будут иметь место только в двух узлах: — W12 и + Wn. Веревочный мн-к, построенный для них при полюсном расстоянии равном 1, имеет форму двух тр-ков и является Л. в углового перемещения. Точное построение Л. в перемещений в фермах и в сочлененных системах связано с большими вычислениями величин упругих грузов. На практике Л. в прогибов приходится пользоваться при испытании сооружений, в частности мостов, где точность теоретическ. расчетов не соответствует точности измерительных приборов. В таких случаях вычисление ординат Л. в прогибов можно делать по приближенным ф-лам инж. Качурина. Подсчеты показали, что расходимость вычислений по приближенным и точным ф-лам для простых решетчатых ферм с дополнительными подвесками и без них не
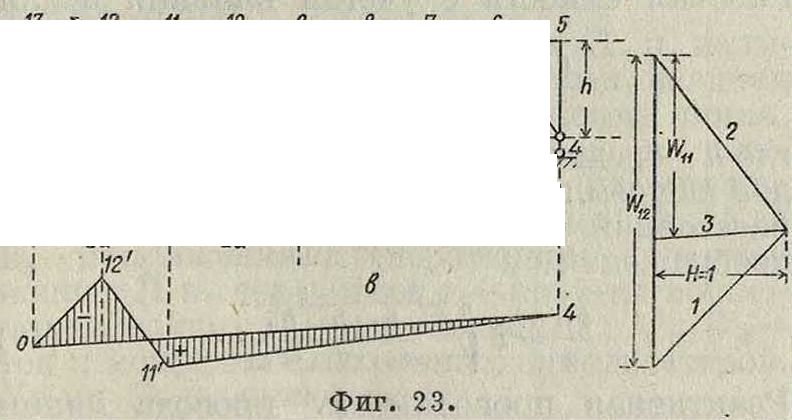
Превосходит 5%, тогда как расходимость между действительными и теоретическими прогибами доходит до 10%.
Обобщенные Л. в Под этим названием известны Л. в., характеризующие собой не влияние груза равного 1, как это имеет место в обычных Л. в., а целой системы грузов, имеющих различную величину и отстоящих друг от друга на определенных и неизменяемых расстояниях. Применение обобщенных Л. в имеет большое значение для испытания мостов. Инж. И. М. Рабинович
I Направление движения предложил строить эти обобщенные линии влияния как веревочный многоугольник от специальной системы грузов. Например если требуется построить обобщенную Л. в для среднего сечения балки от поезда по схеме, показанной на фигуре 24, то балку надо рассматривать под действием трех поездов, обозначенных на том же чертеже цифрами I, 11 и III. Все эти поезда получаются поворотом действительного поезда на 180°. Поезд I ставится своей передней осью над исследуемым сечением; грузы его положительны. Остальные два поезда—реактивные поезда — ставятся своими передними осями над опорами, все, грузы их рав-
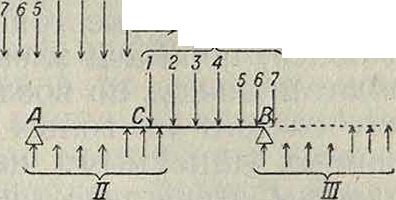
Фигура 24.
ыы половине веса действительных и направлены в обратную сторону. Вся система грузов уравновешена и веревочный многоугольник ее будет замкнутый. Этот веревочный мн-к и представляет собой обобщенную Л. в момента в рассматриваемом сечении. Прием этот м. б. использован для построения любой обобщенной Л. в., соответственно изменяются только число положи тельных и отрицательных поездов и коэ-фициенгы их пропорциональности по отношению к действительшжу поезду. На фигуре 25

Фигура 25.
показана построенная указанным способом обобщенная Л. в усилия в раскосе балочной фермы пролетом 27,0 метров от паровоза серии Щ. Каждая ордината диаграммы соответствует тому положению паровоза, когда передняя ось его стоит над этой ординатой. Особый интерес обобщенных Л. в заключается в том, что они могут быть построены для динамического действия нагрузки (фигура 26). Несомненно, что этот вид Л. в должен получить большое развитие в деле испытания мостов.
Лит.: М то л л е р-Б р е с л а у Г., Графич. статика сооружений, т. 2, ч. 1, пер. с немецкого, 2 изд., СИБ, 1910; Патон Е. Ф. и Горбунов Б. Н., Стальные мосты, т. 1, Киев, 1929; Патон Е. Ф., Таблицы для проектирования деревянных и стальных мостов, Киев, 1929; Прокофьев, Теория сооружения, ч. 1—2, М., 1926—28; Тимошенко С. П., Курс статики сооружений, ч. 1, Л., 1926; К а ч у р и н В., Линии влияния для прогибов и перемещении сквозных ферм, «Труды научно-технического к-та НКПС», М., 1927, вып. 60; Рабинов и ч И., Кинематич. метод в строит, механике, М., 1928; е г о ж е, Нек-рые способы исследования диаграмм, получаемых при испытании мостов, «Труды бюро мостов исслед. научно-техн. к-та НКПС»,М., 1923, сборн. 3;Грио Г., Интерполяционные таблицы для быстрого построения инфлю-ентных линий моментов и поперечных сил, атакже для равномерно распределенных нагрузок и сосредоточенного груза, пер. с нем., М., 1928; Doorentz К., Abreitung d. Einflusslinien, Strassburg, 1921; Lands-b erg Tii., Das Verfahren d. Einflusslinien, 7 Aufl., B., 1920; M arcus H., Die Einflusslinien melirfach gestiitzter Rahmentrager, B., 1915. И. Прокофьев.