> Техника, страница 58 > Линии передачи

Линии передачи

Линии передачи, устройство для транспорта электрич. энергии из места производства в места потребления энергии. Л. п. мо-

гут быть воздушными или подземными. В последнем случае передача энергии производится по подземным кабелям (смотрите Кабель высоковольтный), причем обычно передача электрич. энергии по подземным кабелям производится только на сравнительно небольшие расстояния. При более значительных расстояниях, порядка 100 км и более, передача электрич. энергии производится всегда по воздушным Л. п. Последние состоят из голых проводов, поддерживаемых линейными изоляторами (смотрите Изоляторы электрические), укрепленными через известные промежутки на специальных мачтах-опорах (смотрите Опоры), и соединяющих между собой место генерации электрической энергии (генераторный конец Л. п.) с местом потребления энергии (приемный конец Л. п.). В настоящее время имеются уже осуществленные проекты Л. п., по которым передается до 150 000 kW по одной линии на расстоянии до нескольких сотен км. При передаче столь больших мощностей на такие большие расстояния, во избежание чрезмерных потерь в Л. п. или чрезмерных сечений проводов, необходимо вести передачу при весьма больших напряжениях, достигающих в настоящее время в уже работающих установках до 220 kV. В связи с большой протяженностью Л. п. и значительной величиной применяемых напряжений емкость, линии начинает играть заметную роль в процессе передачи энергии, и картина явлений, происходящих в длинных Л. п., сильно отличается от явлений в коротких линиях.

Электрический расчет Л. п. Омич, сопротивление провода Л. п. равно:

R=~ о, (1)

где I—длина провода, в км, q—сечение провода в миллиметров², ρ—удельное сопротивление материала провода в Ω миллиметров²/км.

Значения удельных сопротивлений различных материалов приведены в таблице 1.

Таблица 1, — Значения ρ для различных материалов.

Красная медь	Алю миний	Бронза	Же лезо	Сталь
мягкая твердо-мягкая ТЯНутая
17,£5 17,5	28,7	19,8—28,3	138	160—204

При переменном токе сопротивление будет несколько больше, вследствие влияния скин-эффекта. В этом случае сопротивление провода будет

R пер .⁼R пост. Л (2)

где К—коэф. скин-эффекта. Для сплошных цилиндрич. проводов и тросов коэф. скин-эффекта равен

К=1 4- 2,03

3,3

+

(3)

где d диам. провода в см. Так как магнитная проницаемость μ ферромагнитных материалов зависит от индукции, то сопротивление биметаллич. проводов зависит от силы тока в них. Зависимость омич, сопротивления биметаллич. проводов (алюминий-сталь) иллюстрируется данными табл. 2.

Таблица 2.— Омическое сопротивление биметаллических проводников.

Сечение проводника, миллиметров2·	На иостоян. токе Q на км при 25°	9 на переменном токе на км при частоте /=50 пер/ск. и 25°
		Плотность тока на А 1мм2
		0	0,62 1,24		1,86	2,17
806 645 524 403 307 254 152 .107 67 42 21,1	0,0365 0,0456 0,0561 0,0727 0,0957 0,116 0,194 0,275 0,437 0,696 1,392	0.0367 0,0458 0.0564 0,0733 0,0963 0,116 0,194 0.276 0,438 0,696 1,392	0,0370 0.0462 0,0567 0,0740 0 0970 0.116 0,194 0,280 0.440 0,696 1,392	0,0380 0,0470 0,0574 0,0740 0,0976 0,116 0,194 0,295 0,448 0.696 1,392	0,0400 0.0488 0,0590 0,0752 0,0995 0,116 0,194 0,316 0,461 0.703 1,392	0,0416 0,0501 0,0601 0,0765 0,100 0,116 0.194 0.324 0,471 0,721 1 ·, 392

Рабочая самоиндукция провода линии при применении транспозиции проводов равна

L=(0,461g ~~ + 0,05 + 0,2 д) · 10-³H,toi, (4)

где г—радиус провода в см, D—расстояние между центрами проводов в см. При трехфазной линии с транспозицией проводов под Ώ следует понимать среднее геометрии, расстояние между проводами

1)=ΫΏ» D_1S · П₂₃, (5)

где Х>₁₂, D₁₃, D₂₃—соответственно расстояния между проводами 1—2, 1—3 и 2—3. Так как для воздушных линий г мало по сравнению с D, то в’ этом случае формула (4) примет вид:

L=(0,46 У + 0,05)-ИГ® Η/iш. (4а)

Индуктивное сопротивление линии

x=‘ZnfLl Ω. (6)

Кажущееся сопротивление провода линии z=Vx² + R² Ω. (7)

Рабочая емкость линии без учета влияния земли

С=°’⁰²⁴¹^⁰:⁶ р/км. (8)

ig-

Рабочая емкость с учетом влияния земли

C=О)

ig - · —

г о где h—среднее геометрическое высот проводов над землей и о—среднее геометрическое расстояний от проводов до их зеркальных изображений.

—=2#>.·*-:b-. (Ю)

а у σ₁₂ · σ₁₃ а₂з

Реактивная проводимость провода линии В=2я/С I мо. (11)

Активная проводимость провода линии передачи д складывается из потерь в изоляторах и потерь на корону.

Потери в изоляторах изменяются прямо пропорционально частоте, выше при деревянных штырях, чем при железных, выше при тумане или мелком дожде, чем в хорошую погоду или при сильном дожде или при обледенелых изоляторах. Результаты измерений потерьв штыревом изоляторе на рабочее напряжение ок. 60 kV даны в таблице 3.

Таблица 3. —Потери в штыревом и з о-

л я τ о p e.
Напряжение, kV	Потерн в W	в изоляторе
		мокром
	сухом
40	7	23
60	16	50
80	31	105
90	41	144

Омическое сопротивление одного элемента гирлянды подвесных изоляторов в сухом виде равно оо, а при смоченной дождем верхней поверхности равно ~ 80 ΜΩ.

Потери на корону в проводе Л. п. равны р=ψ ( + 25) j/£ (Ε-Ε₀γ· 10-^s kW/км; (12)

E—рабочее напряжение линии в kV, Е₀— критич. коронное напряжение;

Е₀=48,9 т₀ δ г lg у kV, (13)

где т—коэф., учитывающий состояние поверхности; для полированных проводов ж== 1; для сплошных неполированных проводов m=0,93 -f- 0,98; для витых проводов т=0,82 -у 0,86; <5—плотность воздуха:

<5=³-^~, (14)

(Ь—барометрическое давление в сантиметров ртутного столба). Зависимость <5 от высоты над уровнем моря дана на кривой фигура 1. Во время снежной бури потери на корону сильно увеличиваются и м. б. вычислены (Е₀ принимают равным 80% его значения при хорошей погоде). Во избежание боль-

Высота над уровнем моря УСЛОВИЯХ бур И ΗΘΟΟΧΟ-

Фигура 1.

димо стремиться к тому,

по формуле (13), было больше Е рабочего напряжения линии.

Характеристиками Л. п. называются кривые зависимости ряда величин от мощности Р₂ на приемном конце линии. Эти величины суть: Р_г—мощность на генераторном конце Л. п., Ij, и 1₂—силы тока на генераторном и приемном концах Л. п., Е₁ и Е₂—напряжения на генераторном и приемном концах Л. п.; cos φ₁ и cos φ₂—коэф-ты мощности на концах Л. π.; η—кпд Л. п.; l_s и W_s— ток и мощность синхронных компенсаторов. Ур-ия Л. п. имеют вид:

E₁=E₂:ChVz^y₀ + y^r^ Jashj/io"^, (15)

h=1₂ ей Уг₀ у_а + ]/^~ Е₀ sh Vz_ay„, (16)

где

z₀=(R + jx) 9

и г/о=(g + i В) мо.

Обычно при отсутствии потерь на корону можно принимать <7=0. По мере удаления от приемного конца Л. п., как это следует из ур-ий (15) и (16), действующие значения силы тока и напряжения будут в общем возрастать, причем возрастание будет идти не беспрерывно, а волнообразно, с длиной волны

А=-

/1/Вс

Т. о. в отдельных случаях при длинных Л. п. сила тока и напряжение на генераторном конце м. б. вследствие влияния распределенной емкости Л. п. менее силы тока и напряжения на приемном конце. Фазный сдвиг между током и напряжением также меняется вдоль Л. п. и м. б. то отстающим, то опережающим. Так как сила тока, напряжение и фазный угол беспрерывно изменяются вдоль линии,то очевидно, что,вообще говоря, потери в линии будут больше джоулевых потерь, рассчитанных по силе тока приемного конца, и падение напряжения в Л. п. будет больше омич, падения напряжения. В тех случаях, когда электрич. и магнитная энергии в Л. п. полностью кюмпенсируют друг друга, потери в Л. п. будут равны омич, потерям. Это условие удовлетворяется при нагрузке, равной

f с 1 ‘J00 У L

Ш,

где Е₂ — фазное напряжение на приемном конце Л. п. в V. Если длина линии передачи

1о=’

то есть равна четверти длины волны, то условия компенсации электрической и магнитной энергии удовлетворяются при всех нагрузках. Ур-ия (15) и (16) имеют сложный вид и неудобны для расчетов, почему ими рекомендуется пользоваться только при расчете очень длинных Л. п. Для линий длиной до 500 км можно с достаточной точностью заменить ур-ия (15) и (16) следующими ур-иями:

Ε₁=Ε₂{ί+?ψ)+ζ_ΰΙ₂(ΐ+^ζ-ψ)=Α+ΐΒ, (17) Ii— 1-г (l + Щ + У_аЕ₂(l + ^ζψ)=С + jD (18) или в более удобной для расчета форме:,

-Е¹!=а { EJ + I₂z₀ cos (σ -φ₂)} +

+ ja [Ε₂βτ + Ι₂ζ₀ sin (σ — φ₂) | =A+jВ, (19) I₁=γ1₂ cos (φ₂ ~τ)-Ε₂Βξα +

+ j { Ε₂Β α — γΙ₂ sin (φ₂ - τ) }=C + jD. (20)

В уравнениях (19) и (20) все величины (кроме Е_х и Ιχ) представляют собою абсолютные значения, т. e. z₀=VR‘ + ж² и тому подобное.

α= 1-^Взс, (21)

(22)

(23)

(24)

(25)

arctg j. (26)

О 1 ^Вх

β ^{= 1}~Α~

Вх

2 ¹ RB _ 2 “

У=1-τ=arc tg

кв

2

., RB RB

arctg „ =, =

. д ⁺ σ=arc tg--_}

RB

Bx

При частоте f=50 можно с достаточной точностью принять:

а= 1 -0,1935 г2· 10-«,	(21а)
β=1 —0,387 г2· 10-«,	(22а)
γ=1-0,581 V · Ю-е.	(23а)

Л. п. оканчивается у трансформаторов, в которых сопротивление, самоиндукция и емкость уже не распределенные, как в линии, а сосредоточенные. При необходимости определения напряжений и т. д. на стороне низкого напряжения. необходимо учитывать влияние трансформаторов. Расчет можно произвести двумя ступенями, рассматривая сначала явление в линии и накладывая затем на них падение напряжения и т. д. в трансформаторах. Иногда удобно принимать постоянные трансформаторов не сосредоточенными, а распределенными и прибавлять их непосредственно к постоянным линии, что сводит расчет к одной операции без большого ущерба в точности, в особенности при коротких линиях. Намагничивающий ток нормальных силовых трансформаторов изменяется в пределах 3—6% от тока полной нагрузки, потери в железе V₂—1% и потери в меди ³/₄—1¹?4% ^от номинальной мощности трансформатора. Омичгск. падение напряжения 1R составляет обычно ³/₄—1% от номинального напряжения трансформатора. Реактивное падение напряжения 1х в % зависит от напряжения (смотрите Короткое замыкание). По вышеприведенным данным могут быть легко вычислены необходимые для расчета постоянные трансформаторов.

Для сравнительно коротких линий, не длиннее 65—80 км, и напряжений, не превосходящих 50—60 kV, влиянием емкости и утечки можно пренебречь, причем уравнения Л. гг. примут вид:

Б?!*-(27) h -i.· (28)

Нормально при передаче электрич. энергии по Л. п. напряжение у приемного конца должно поддерживаться постоянным при всех нагрузках. Это м. б. достигнуто например путем изменения напряжения генератора. Относительное изменение напряжения генератора. в % от постоянного напряжения приемника при изменении нагрузки от холостого хода до полной, называется регулированием линии:

ΔΕ=^§^·100%. (29)

Величина ΔΕ зависит гл. обр. от реактивности линии. В целях удобства эксплоата-ции регулирование линии не должно превосходить 10—15% и максимум в исключительных случаях 22%. Регулирование линии м. б. вычислено по вышеприведенным ур-иям Л. п. (15), (19) или (27), в зависимости от длины линии. С достаточной точностью регулирование линии может быть вычислено по следующей ф-ле:

ΔΕ= а[тг₀ cos(ff-<p₂) + (30)

где

(12—ТОК на приемном конце при полной на грузке). Т. к. при постоянном напряжении на приемном конце Л. п. напряжение на генераторном конце зависит от козф-та мощности, то, если регулирование линии получается более допустимых пределов, возможно поддерживать постоянные напряжения на обоих концах Л. п. путем искусственного изменения коэф-та мощности. Такое изменение коэф циента мошности м. б.· выполнено при помощи синхронных компенсаторов, то есть синхронных двигателей, дающих, как известно, при недовозбуждении отстающий, а при перевозбуждении опережающий ток. Двайт (Н. В. Dwight) показал, что для поддержания постоянства напряжения на приемном конце линии при постоянном напряжении на генераторном конце необходимо, чтобы конец вектора тока 1_г скользил по кругу, координаты центра которого и радиус зависят от постоянных линии и напряжения. Координаты центра круга синхронных компенсаторов и радиус круга м.б. с достаточной точностью вычислены по следующим ф-лам:

α= ~Ьх0 C0S(?> + !-T0),	(32)
b=lj~~ Sin (?> + { - τ0),	(33)
г-“, Ζ0α где	/*““ч СО *
т τ°= β7 ’	(35)
β=Х-Щ-β.	(36)
Для линий не длиннее 200—300км можно с достаточной точностью пользоваться вместо ф-л (32) и (33) ф-лами „ — (37) ζ0

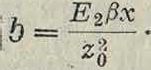
(38)

Окружность круга синхронных компенсаторов

Ток синхронных компенсаторов, а^тследовательно и их безваттная мощность, могут быть определены путем построения диаграммы (фигура 2). При холостом ходе синхронные компенсаторы посылают в линию отстающий ток, к-рый с увеличением нагрузки постепенно уменьшается, доходит до нуля и при полной нагрузке становится опережающим.

Приувеличении напряжения Е, отстающий ток синхронных компенсаторов увеличивается, жающий уменьшается.

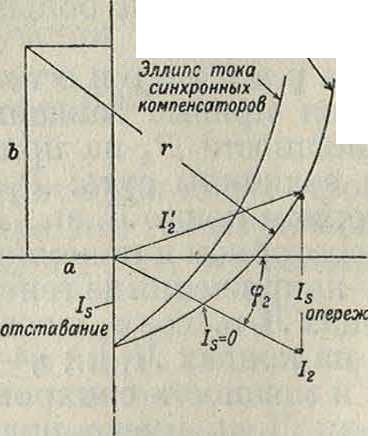
Фиг. а опере-

Наивыгоднейшим является такое напряжение генераторного конца Е_ь при котором максимальный опережающий и отстающий токи равны, т. к. очевидно, что мощность синхронных компенсаторов при этом получается минимальной. Однако в виду неустойчивости работы сильно недовозбужденных синхронных двигателей на практике обычно выбирается Е_у, т. о., чтобы максимум отстающего тока равнялся 60—75% максимума

опережающего тока (тока синхронных компенсаторов при полной нагрузке). Выбор напряжения Е_х м. б. сделан на диаграмме фигура 2 путем подбора величины г, удовлетворяющий вышеуказанным условиям. Тогда напряжение Е, находится по формуле (34).

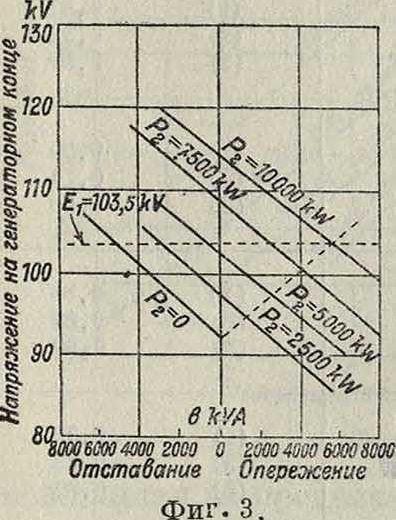
Другой способ определения мощности синхронных компенсаторов заключается в следующем. Строятся кривые зависимости генераторного напряжения от коэф-та мощности приемника при различных нагрузках. Для данной постоянной величины Е₂ и cos <р₂коэф-т мощности на приемном конце зависит от мощности синхронных компенсаторов, которая для удобства и откладывается на оси абсцисс. Построенные т. о. зависимости (фигура 3) практически представляют собою прямые линии, за исключением очень больших перегрузок и малых коэф-тов мощности cos φ₂. В виду этого для построения зависимости достаточно для каждой нагрузки вычислить две точки, соответствующие следующим условиям: 1) мощность синхронных компенсаторов Ж₈=0 и 2) коэф-т мощности приемного конца равен 1. Пересечение зеркального изображения кривой для холостого хода относительно оси TE_s=0 с кривой полной нагрузки дает точку, определяющую мощность синхронных компенсаторов и напряжение генераторного конца при условии равенства отстающей и опережающей мощностей компенсаторов. При неравенстве отстающей и опережающей мощности необходимо только соответственно изменить ось, относительно которой строится зеркальное изображение кривой холостого хода. Пересечения кривых для других нагрузок с прямой линией, соответствующей полученному указанным способом напряжению Е_х, дают точки, определяющие мощность синхронных компенсаторов при этих нагрузках. Суммируя найденное значение тока синхронного компенсатора с током нагрузки (геометрически), получаем полный ток на приемном конце Л. п. Зная полный ток приемного конца, характеристики Л. п. можно вычислить но приведенным выше ур-иям, например (19) и (20). Потери в синхронных компенсаторах 3—4% от их реактивной мощности.

Перенапряжения в Л. п. и выбор изоляции. Перенапряжения в Л. π. могут быть разбиты на следующие группы: 1) перенапряжения внутреннего характера вследствие процессов включения и выключения; 2) перенапряжения вследствие заземляющих дуг; 3) перенапряжения атмосферного характера. Перенапряжения при включении и выключении разомкнутой линии обычно не превосходят 70—100% от номинального напряжения Л. п. В отдельных случаях были зарегистрированы перенапряжения, в 6 раз превышающие номинальное фазное напряжение Л. п. Наиболее неблого приятные условия получаются при оперативности на стороне высокого напряжения. Выключение и включение нагрузки вызывает обычно очень небольшие перенапряжения. При выключении коротко-замкнутей линии запасенная магнитная энергия - --- перехо-дит в электростатическ. энергию ——, то есть L1* СЕ2

Т.о. возникающие при этом перенапряжения будут тем больше, чем меньше емкость С и чем больше ток короткого замыкания I.

Выключение короткого замыкания наиболее опасно при оперативности на стороне низкого напряжения. Судя по произведенным наблюдениям на работающих америк. линиях, перенапряжения при выключении коротких замыканий не превосходят 5—6-кратной величины от нормального фазного напряжения Л. п. Такие перенапряжения для современной изоляции Л. п. и аппаратов нормально не представляют опасности. Перенапряжения вследствие заземляющих дуг, возникающие при генерировании дугой высокочастотных колебаний, наиболее опасны на системах с изолированной нейтралью. Ниже приведены теоретические максимальные напряжения, могущие быть полученными при различных условиях и вычисленные Клемом (I. Е. Clem).

Условия расчета

Кратность перенапряжения по отношению к фазному напряжению Л. п.

Без учета затухания. 7,5

С учетом затухания. 5,7

С учетом затухания и емкости между проводами. 5,5

При заземлении нейтрали через сопротивление не больше критического .. 2,5

При наглухо заземленной нейтрали .. 1,0

Критич. сопротивление в нейтрали, при котором перенапряжение вследствие заземляющих дуг не превосходит 2,5-кратной величины от фазного напряжения Л. п., может быть вычислено по следующей ф-ле, выведенной Кларком (Е. Clark):

R =

10 £2

^ж-^ж2(т§b^к1в

|/з Е

~100 Pi

(39)

kl_a

где Е—линейное напряжение в kV, х—реактивность системы до места аварии в % от мощности Р_;; 1_е—зарядный ток в заземляющей дуге; к—отношение отстающей составляющей тока короткого замыкания к 1_С. Для быстрого гашения дуги проф. Петерсеном было предложено заземлять нейтраль трансформаторов через реактивную катушку, подобранную т. о., чтобы скомпенсировать емкостный ток в заземляющей дуге. Однако в условиях дождя, при наличии заметной активной составляющей тока заземления, катушка Петерсена не может вызвать гашения дуги и даже, наоборот, может сама явиться источником значительных перенапряжений. Наилучшим способом борьбы с заземляющими дугами является все же заземление нейтрали или наглухо или через со-

противление, не превосходящее критической величины (ф-ла Кларка).

Наиболее опасными для изоляции Л. п. и оконечных подстанций являются перенапряжения атмосферного характера. Атмосферные перенапряжения носят всегда характер импульсов или быстро затухающих колебаний очень высокой частоты.

Возникновение перенапряжений атмосферного характера м. б. представлено след, обр. Когда над проводом Л. п. находится заряженное грозовое облако, то на проводе индуктируется связанный заряд противоположного знака, плотность которого в точке х будет

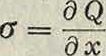
где с—емкость провода на единицу длины, h—высота провода над землей, д—градиент земного потенциала. При мгновенном разряде заряда облака заряд на проводе Л. п. освобождается, причем потенциал провода будет

Так как в действительности облако не может разрядиться мгновенно и разряд длится конечный промежуток времени, то действительная амплитуда перенапряжения, возникающего на проводе Л. п. при разряде грозового облака, будет

V=agh, (40)

где коэф. α ^ 1 и зависит от скорости и закона разряда облака и распределения связанного заряда вдоль провода Л. п. После освобождения заряда последний начинает двигаться в две противоположные стороны, образуя две блуждающих волны, амплитуда напряжения которых будет

7₁=agfe, (40а)

причем коэф. а ^ 0,5. В табл. 4 приведены значения коэф-тов a и a в предположении равномерного распределения связанного заряда вдоль провода Л. п.

Т а 0 л. 4.—3 н а ч е н и я a и а.

Время разряда облака на 95% в у ск	Длина связанного заряда в м
	600		1 200
	a	a	a	а
0	1	0,5	1	0,5
1	0,61	0,42	0,72	0,48
2	0,44	0,34	0,58	0,42
3	0,33	0,27	0,47	0,37
4	0,27	0,23	0,40	0,32

Градиент потенциала земли может при сильных грозах достигать значений до 330 kV/ж.

Для уменьшения амплитуды атмосферных перенапряжений применяется защита линий при помощи заземленных тросов, протянутых над проводами Л. п. Отношение амплитуды перенапряжения при защите Л. п. заземляющими тросами к амплитуде перенапряжения без тросов называется к о э ф и ц и-ентом защиты. Значения коэфициента защиты при различных расположениях проводов и тросов даны в таблице 5. Из рассмотрения табл. 5 очевидно преимущество горизонтального расположения проводов, так как |

в этом случае мы кроме понижения высоты подвеса провода улучшаем также и защитное действие троса. При двух заземленных тросах и горизонтальном расположении проводов коэф. защиты м. б. принят равным 0,37.

Таблица 5К оэфициенты защиты.

Расположение проводов О » тросов Q	Коэфпциент защиты
• 000 1 2 3	(1) 0,45 (2) 0,45 (3) 0,52
9 О ООО	(1) 0,37 (2) 0,32 (3) 0,37
9 ООО	(1) 0,50 (2) 0,44 (3) 0,50
9 9 9 ООО	(1) 0,30 (2) 0,27 (3) 0,30
9 О 90 О 9	(!) 0,32 (2) 0,28 (3) 0,32
О О о 9 о о о	(1) 0,42 (2) 0,52 (3) 0,62
9 9 Λ О О о о о о	(1) 0,33 (2) 0,39 (3) 0,48
9 9 9 о о о о о о	(1) 0,28 (2) 0,33 (3) 0,41

Выбор изоляции Л. п. делается обычно по существующим нормам, то есть выбирается такой изолятор или число элементов гирлянды изоляторов, разрядное напряжение которого удовлетворяет условиям норм. Однако так как нормируется разрядное напряжение при промышленной частоте, а наиболее опасные перенапряжения носят всегда характер импульсов, то выбор изоляции по нормам не всегда обеспечивает бесперебойную работу линии передачи. Для полного обеспечения линии от перекрытия изоляторов изоляцию линии выбирают, исходя из импульсного разрядного напряжения и высоты подвески провода над землей.

Зависимость величины разрядного напряжения от числа элементов в гирлянде шарнирных изоляторов (0 элемента—254 миллиметров и расстояние между элементами—146 миллиметров) при импульсе и при промышленной частоте дана в графической форме на фигуре 4. При расчете амплитуды атмосферных перенапряжений градиент земного потенциала в большинстве случаев достаточно принимать равным 250 kV/ж и только в местностях с усиленной грозовой деятельностью увеличивать эту цифру до 330 kV/ж.

Очень сильная изоляция Л.п. может создать благоприятные условия для попадания волн с большой амплитудой на подстанцию. Во избежание этого ближайшие к подстанции участки Л. п. следует делать с ослабленной изоляцией и с усиленной защитой тросами. Длину ослабленного участка выбирают исходя из” того, чтобы волна перенапряжения,

Фигура 4.

возникшая за пределами этого участка, успела достаточно затухнуть до попадания на подстанцию. Затухание вотны вдоль линии м. б. вычислено по формуле (эмпирической):

е =

ер

0,0001 (е₀ +1^:

(41)

где е₀—начальн. амплитуда волны в kV; I—

расстояние до места возникновения волны в км. Максимальное возможное значение е₀для любой линии будет импульсное разрядное напряжение изоляторов. При выборе подвесных изоляторов необходимо иметь в виду, что распределение потенциала вдоль гирлянды происходит неравномерно вследствие влияния емкостей арматуры изолятора относительно земли и провода Л. п.

Выбор расстояния между проводами. Выбор расстояния между проводами Л. п. должен быть произведен т. о., чтобы при максимальном возможном сближении проводов разрядное напряжение между ними при плотности воздуха δ=0,9 (условия бури) было не менее полуторного рабочего напряжения Л. п. Разрядное напряжение по отношению к нейтрали м. б. вычислено по формуле Пика:

Ems ~ Qvis ^ ^ γ kV действ. > (42)

причем при больших расстояниях у > 30

д_т=21,2 <5 m (1 + - °;^{01 D}Л kV /см (43)

у dr - r

при у < 30

д_тч=21,2 δ т (l + °-’^s=) kV/см. (44) У 6г

Сближение проводов может произойти или вследствие их раскачивания ветром, или вследствие неодинаковой нагрузки вертикально расположенных проводов, или вследствие раскачивания проводов электродина-мич. взаимодействием токов короткого замыкания. При горизонтальном расположении максимальн. сближение проводов будет при их асинхронном раскачивании. При расчете качания проводов под действием ветра достаточно принимать расхождение фаз качания на 90°. При вертикальном расположении проводов наиболее опасным является сброс гололеда на одном пролете нижнего провода. Анализ вопроса показывает, что в этом случае сближение проводов практически не зависит от пролета Л. п.

При приблизительных расчетах можно определить расстояние между проводами при горизонтальном расположении их по формуле, предложенной инж. А. А. Глазуновым:

D=(a^+BE) см, (45)

где I—длина пролета в м, Е—линейное напряжение в начале линии в kV. При IS < 40 kV: А=1,4, В=1; при Е > 40 kV:

А=0,75, В=2,2.

Вертикальное расстояние между проводами Л. п. может быть определено по формуле инж. А. М. Залесского:

s„.=(120 +0,155 В¹’⁵) см. (46)

Расстояние между проводами и частями опор м. б. определено по формуле проф. А. А. Смурова:

d=(15,7 + 5,75 VE) cm, (47)

причем в случае подвесных изоляторов принимается отклонение гирлянд на 45°.

Ф-лы (45), (46) и (47) не учитывают отклонения проводов электродинамич. силами при коротком замыкании. В этом случае максимальное горизонтальное отклонение провода м. б. вычислено из ур-ия:

0.29/₀-у In -- ⁺-V^{5 xm}-=2 890γ~ +2-0,092^, (48)

где x_m—максимальное горизонтальное отклонение провода в см, /₀— начальная стрела провеса провода в см, σ—начальное напряжение в материале провода в килограммах/см², к— отношение веса провода с гололедом к весу голого провода, t—время в ск., необходимое для достижения максимального отклонения. На основании произведенных Петерсоном и Мак Крекеном опытов можно принимать в среднем ί=0,3—1,2 ск. Ур-ие (48) легче всего решать путем подбора.

Устойчивость работы Л. п. Каждая данная Л. п. имеет нек-рую предельную мощность, которую можно передать по Л. π. I При переходе через ? этот предел устой- I чивость работы на * рушается и проис- 1 ходит выпадение из | синхронизма. Ус- § тойчивость работы | тем меньше, чем больше кажущееся сопротивление между генератором и мотором. На больших высоковольтных Л. п. зарядный ток понижает необходимое возбуждение машины и может таким образом привести к уменьшению устойчивости работы. Поэтому максимальная мощность, которая мож т быть передана по Л. п. при увеличении числа цепей, сначала увеличивается, а потом снова падает (фигура 5).

г з 4 5 6 7 8 9 Число линий

10 11

Т. Э. rn. XII.

δ

Необходимо различать устойчивость работы Л. п. при установившемся и при устанавливающемся режиме работы. Устойчивость работы при установившемся режиме работы сильно зависит от системы регулирования напряжения и от типа возбудителя. При замене Л. п. по Кенелли эквивалентной π линией максимальная мощность, которая м. б. передана по Л. п. при установившемся режиме работы, м. б. вычислена по ф-ле, предложенной Никле (С. A. Nickle):

Е 2		(-1	(*Ч)
@	м	, эс Χί+ν	(*2+|)

где Е—линейное напряжение передачи, х — эквивалентная реактивность генератора, ж— эквивалентная реактивность мотора, х—эквивалентная реактивность линии. В виду наличия многих влияющих и неучитываемых факторов точный расчет максимальной мощности возможно произвести лишь в простейших случаях. Расчет устойчивости работы Л. п. при устанавливающемся режиме работы представляет собою чрезвычайно сложную задачу и обычно не может быть произведен. Испытания работающих систем показали, что предел устойчивости работы Л. п. при устанавливающемся режиме работы составляет от 30 до 60% от Р_тах при установившемся режиме.

Механический расчет Л. п. Расчет проводов имеет целью определить тяжения и провесы проводов при различных условиях для решения задач по выбору расположения проводов, трасировке линий, монтажу и тому подобное. Провес проводов определяется по ф-ле:

/-I“. (⁵°)

где д—нагрузка провода в килограммах/м, I—пролет в м, σ—напряжение в материале провода в килограммах/мм², q—сечение провода в миллиметров². Если обозначить р=^я кг/м миллиметров², (51)

то по заданным начальным условиям (σ₀, р₀и ίο) напряжение в материале провода при любых условиях может быть определено из уравнения:

1 р“1*Е i vli*E

⁰ !4 ⁰⁰ 24 σ

-aE(t-t₀)T^a-f, (52)

где E—модуль упругости материала проводов, а—температурный коэф. линейного расширения материала проводов, ί—темп-pa в °С, (5—изменение пролета, причем знак —соответствует уменьшению пролета, а + увеличению. Механические свойства многопроволочных проводов по нормам ЦЭС приведены в таблице 6.

Максимальное напряжение в материале провода при пролете больше критическ. имеет место при ί=5° и нагрузке гололедом и ветром, а при пролетах меньше критического при ί=t_wdn. Критический пролет определяется по формуле: ____

^{= σ}ηιαχ | ^а (tmfn ^о) р2 _ р2 (эЗ)

Знак 0 соответствует условиям гололеда. Максимальный провес проводов может иметь

Табл, б.—М еханические свойства многопроволочных проводов.

Материал	Уд. вес У	а	Е, кг/мм“	Допуск, в матер промешу т. пролеты	напряж. ., кг/мм8 анкеро ванные пролеты
Медь.	8,9	16-10-“	1,1-10*	2Э	13
Алюминий.	2,7	23-10-“	0,6 -1 о4	10	7
Сталь.	7,8	12-10-·	ϊ,8·101		—

место или при ί=t_max (если t_max > t_Kp_) или при нагрузке гололедом и ί= -5° (t_max<t_K ). Критич. ί° м. б. рассчитана по ф-ле:

ίкр. ⁼ + ^атах ^ (l ~ * (54)

По нормам ЦЭС следует принимать толщину гололеда 1 сантиметров при уд. весе льдα= 0,9 и давление ветра на проводα= 24 килограмма/м², относя давление ветра к проекциям провода. При раскачивании проводов ветром максимальный угол качания имеет место при ί=— 5° и нагрузке гололедом толщиной

<5=КоТООЗб γ q - 0,25^- 0,5 d, (55) где d—диам. провода в см. Если по формуле (55) <5>1 см, то в расчет следует вводить (5=1 см.

Нагрузки, действующие на опоры Л. п., определяются по нормам ЦЭС в соответствии с вышеизложенным. Наиболее тяжелым случаем является односторонний обрыв части проводов (обрыв двух проводов из трех). При определении приложенных в этом случае к опоре сил тяжений проводов при расчете промежуточных опор с подвесными изоляторами необходимо считаться с уменьшением тяжения проводов вследствие отклонения гирлянд. Уменьшение тяжения проводов в этом случае будет тем незначительнее, чем больше пролетов имеется между анкерными опорами. Т. к. опоры имеют нормально некоторую гибкость, то необходимо учитывать также и отклонение вершины опоры, также уменьшающее натяжение проводов. Расчет уменьшения натяжений вследствие отклонения гирлянд и верхушек опор производят проще всего путем подбора, задаваясь условиями на анкерной опоре и проверяя по ним условия на последней опоре у оборванного пролета. При наличии заземленного троса необходимо считаться с тем, что часть нагрузок берет насебя трос. После определения действующих на опору нагрузок расчет опор производится нормальными методами строительной механики.

Экономический расчет Л. п. Задача снабжения электрич. энергией промышленных центров может быть разрешена или постройкой электрич. станции на месте нагрузки и транспортом топлива для питания такой станции или же непосредственным транспортом электрич. энергии через Л. п. При экономии, обосновании целесообразности постройки Л. п. могут встретиться два основных случая. При передаче энергии от тепловой электрич. станции необходимо сравнить стоимость транспорта электрич. энергии по Л. п. со стоимостью транспорта топлива. При передаче электрич. энергии с гидроэлектрич. станции необходимо сравнивать стоимость энергии от гидростанции (стоимость электрич.энергии на шинах станции + стоимость передачи энергии по Л. п.) со стоимостью энергии на местной электрической станции, работающей на местном или привозном топливе. Обычно наиболее рентабельной является передача электрич. энергии от гидростанций и от станций, работающих на дешевом и малокалорийном топливе (торф, сланец, штыб и тому подобное.), транспорт которого обходится чересчур дорого. При рассмотрении вопроса необходимо также иметь в виду разгрузку ж.-д. транспорта при сжигании топлива на месте добычи и транспортировании электрической энергии. Задача проектирования и постройки Л. п. заключается в выборе таких элементов Л. п. и их комбинации, при которых ежегодные расходы на передачу энергии являются минимальными. При этом общая задача распадается на ряд отдельных частных задач.

Для каждой линии имеется нек-рый пролет, называемый экономическим пролетом, при к-ром ежегодные расходы на опоры и изоляторы минимальны. Экономил. пролет определяется путем расчета стоимости одного км Л. п. (без проводов) для различных пролетов, на основании чего строится кривая зависимости ежегодных расходов от длины пролета и находится ее минимум. В среднем экономии. пролет получается обычно для жестких металлич. опор равным:

При Е=35 kv.. 150 — 200 м

» Е=60 ».. 2Э0 — 250 ь

» Е=100 ».. 52.) — 27) »

» Е=220 ».. 250 — 300 »

При гибких опорах экономил, пролет получается. обычно в Н/₂—2 раза меньше.

Стоимость проводов· Л. п. пропорциональна весу материала проводов, то есть пропорциональна сечению провода. Т. к. увеличение сечения проводов увеличивает стоимость проводов и опор, но уменьшает стоимость потерь в линии, то для каждой Л. п. существует некоторое наивыгоднейшее сечение провода, при котором ежегодные расходы получаются минимальными. Не учитывая влияния сечения проводов на стоимость опор, наивыгоднейшую плотность тока в линии можно найти по Кельвину из ф-лы:

Ш· <⁵⁶) где q—сечение провода,в миллиметров², δ—уд. в материала провода, р—стоимость одной т проводов, tv—стоимость одного kW-года электрич. энергии, о—удельное сопротивление материала провода, а—ежегодные %-ные отчисления на провода, 1_е—средняя квадратичная сила тока в линии за год. Если обозначить имеющуюся в линии силу тока через Ι_Χι то средняя квадратичная сила тока будет

.-УШ <“>

Т. к. формула (56) не учитывает стоимости опор, увеличивающейся при увеличении сечения провода, то в действительности наивыгоднейшее сечение будет всегда меньше рассчитанного по формуле (56). В виду этого можно рекомендовать пользоваться этой ф-лой только для ориентировки, для получения верхнего предела возможного сечения провода, и находить после этого наивыгоднейшее сечение

например в сетях в провода путем составления параллельных смет для нескольких вариантов и сравнения получающихся стоимостей.

Чаще всего применяются провода из следующих материалов: красная медь твердотянутая; красная медь в виде полых проводов; биметаллическ. провода (обыкновенно алюминий со стальным сердечником); алюминиевые провода без стального сердечника применяются значительно реже; железные провода применяются только на неответственных линиях небольшой мощности, сельских местностях.

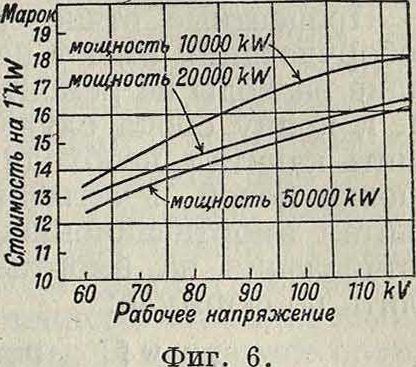
Стоимость оконечных подстанций после разработки схемы коммутации, выбора типа подстанции и составления спецификации аппаратуры легко определяется по прейскурантам и предложениям разных фирм. Для предварительных сравнительных расчетов можно пользоваться данными стоимостей, приведенными в виде кривых на фигуре 6 (стоимость трансформаторных подстанций в Германии, по проф. Клингенбергу), на фигуре 7 (стоимость открытых подстанций в Америке) и на фигуре 8 (стоимость трансформаторов и распределительного устройства по А. Стиллу). Общие ежегодные расходы по Л. п. и оконечным подстанциям складываются из следующих элементов: расходы на обслуживающий персонал; процентные отчисления на капитал; процентные отчисления на амортизацию оборудования; процентные отчисления на ремонт; стоимость потерь в линии, тран- ₄сформаторах и синхронных компенсато- |з рах. Расходы на об- -служивающий персо-нал малы по сравне-1 нию с остальными 1; расходами и при про-оптировании могут о.

Долларов 15

*11

I⁷

I⁵

3,

мощность 10000 k W

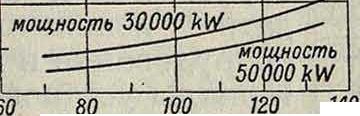
100 120 Рабочее напряжение Фигура 7.

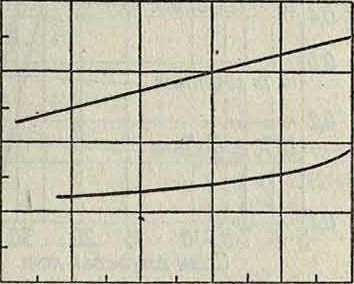
10 20 30 40 50 60 70 80 90 100кЧ Рабочее напряжение

Фигура 8.

не учитываться. Конечно при окончательном определении стоимости передачи электрич. энергии эти расходы также должны быть учтены. Процентные отчисления на капитал зависят от стоимости капитала в данный момент в данной местности. Учитывая %, наросшие на капитал за время постройки до начала экс-плоатации, %, к-рый необходимо отчислять на затраченный капитал при стоимости капитала р% и сроке постройки п лет, будем иметь:

*-Μ(¹+&)"+(¹+£Γ +

+ (^г + ϊοδ) + i¹ + ιοο)] % ·

+

Ф-ла (58) предполагает отпуск денег на постройку равными суммами в начале каждого года постройки. Для уменьшения процентных отчислений на капитал следует стремиться к уменьшению срока постройки и к сосредоточиванию главных расходов к концу постройки.

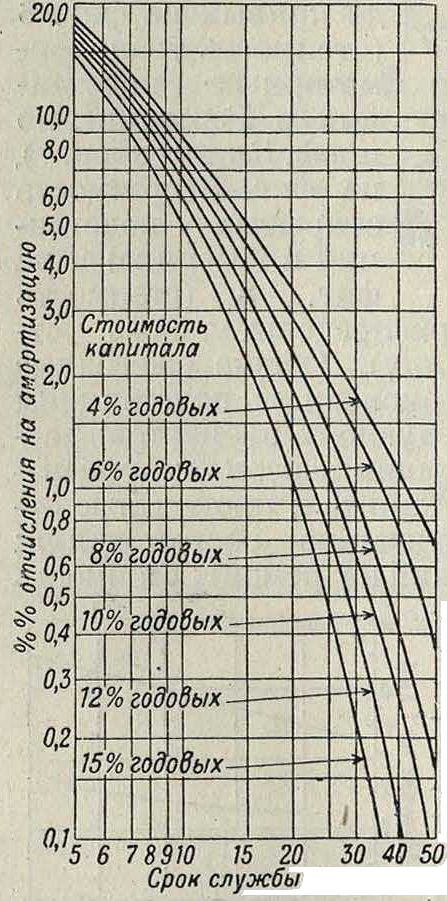
Процентные отчисления на амортизацию оборудования имеют целью покрывать текущие расходы на ремонт частей оборудования и к концу срока службы сооружений накопить капитал, необходимый для замены установки новой. Учитывая сложные % на капитал амортизационного фонда, процентные отчисления на. амортизацию можно определить по формуле:

^й=7 [ά+^ст] ‘ ¹⁰⁰% ’ (5»)

где р—стоимость капитала в долях единицы; п—срок службы установки в годах; J—стоимость сооружения; w—стоимость замены по окончании срока службы старой установки новой;

w=J + R — S,

где R—стоимость приготовления места под постройку новых сооружений (расчистка места, разборка и тому подобное.), S—стоимость установки после окончания срока службы ее, то есть та сумма,за которую можно продать изношенное оборудование и материалы установки. В табл. 7 приведены данные относительно сроков службы отдельных элементов сооружений и стоимость их Sпосле окончания срока службы.

На кривых фигура 9 приведг на зависимость процента. отчислений на амортизацию от срока службы сооружения в предположении S=R. Процентные отчисления на ремонт зависят от лт. характера отдель-Фигура 9. ных элементов ус тановки и от напряженности работы. Для различных частей установки ориентировочно можно принять процентные отчисления по след, данным:

Отчисления

Наименование на ремонт в %

Динамо, турбины, сети внутри помещений .. 1,5

Трансформаторы.. 1,5—3

Деревянные опоры.. 2

Железные опоры.. i

Распределительное устройство. 2

Здания.. 0,7—1

Воздушные сети.. 4

Выбор наивыгоднейшего напряжения является наиболее существенным при экономия, расчете Л. п. Ориентировочно наивыгодней-

J Таблица 7.—С рок службы элементов сооружения и стоимость их S по окончании срока службы.

Наименование элементов сооружения	Срок службы в годах	S в % от первоначальной стоимости
Здания ..	75	5
Паровые турбины. Паровые машины и конден-	15—20	10
саторы.. Синхронные компенсаторы, трансформаторы, возбудите-	12	10
ли и тому подобное..	15—20	10
Распределит, устройство.	12	5
Альтернаторы.	10—20	10
Аккумуляторные батареи.	10—20	10
Водяные турбины.	30	—
Железные опоры.	40—50	—
Деревян. опоры в бетоне.	20	—
Деревни, опоры в земле.	10—18	—
Воздушные линии.	20 ·	—

шее напряжение может быть рассчитано по эмпирической формуле:

Е — 4,34V I + 0,016ΪΡ kV, (60)

где l—длина линии в км я Р—передаваемая по линии мощность в kW. Ф-ла Стилла, как и другие предложенные эмпирич. ф-лы, применима только для предварительных расчетов, так как многие существенные факторы ф-лой не учитываются. В виду этого для нахождения наивыгоднейшего напряжения необходимо идти путем сравнения нескольких параллельных вариантов и пользоваться ф-лой (60) только для предварительного определения наивыгоднейшего напряжения и ограничения числа подлежащих сравнению вариантов.

Сравнение вариантов передачи приводит к параллельному расчету нескольких вариантов и составлению смет стоимости сооружений и стоимости передачи энергии, что м. б. выполнено согласно вышеизложенному. При этом необходимо помнить, что наивыгоднейшим является не тот вариант, который дает наименьшую стоимость сооружений, а дающий наименьшую стоимость передачи энергии; только в редких специальных случаях следует отдавать предпочтение варианту с меньшей первоначальной затратой капитала.

Лит.: Стилл А., Передача электрич. энергии, М., 1925; К а π п е р Ф.,Электропередача. Сооружение воздушных линий, М., 1927; Смуров А. А., Электротехника высокого напряжения и передача электрич. энергии, Л., 1925; УгримовБ. И., Техника высоких напряжений, вып. 1—4, М.—Л., 1924—26;×р у-щ о в В. М., Электрич. линии и сети, Харьков, 1926 (литогр.); Эпштейн Г. Л., Линии передачи электр. энергии переменными токами, ч. 1, Киев, 1925; М а ш-киллейсон Л. Ё., Вспомогательные графики и таблицы для расчета линий электропередач, Л., 1928; Сирот и некий Л.И.,Перенапряжения,Москва, 1924; Эпштейн Г. Л., Перенапряжения на электрич счих установках, Киев, 1927; Юрьев М. Ю., Влияние высоковольтных линий на линии связи, М., 1929; Сушкин Н. И. и Глазунов А. А., Новые конструкции высоковольтных линий передачи, М.—Л., 1929; Глазунов А. А., Линии электропередачи, ч. 1, М., 1928; Залесский А. М., К вопросу о выборе расстояний между проводами линий передачи, «Электричество», Москва, 1928; ЦепляевП. П., Индуктивное влияние трехфазных линий сильного тока на параллельные им линии слабого тока, там же, 1923; А з б у к и н И. А., Влияние линий передач электрич. энергии на линии слабого тока, там же, 1925; СЭТ, Справочная книга для электротехников, т. 3, Л., 1928; Ф а у л ь Ф., Справочник по электротехнике,т. 3, М., 1929; Электротехнические правила и нормы, М., 1929; Buch A., TheoriemodernerHoehspan-mmgsanlagen, 2 Aufl., Mch. u. Berlin, 1922; Z ip p H., Handbuch der elektrischen Hochspannungsteelmik,

5 Aufl., Leipzig, 1923; К у s e г Н., Die elektrische Kraftiibertragung, 2 Aufl.,B 2, B., 1921; Mauduit A., Installations blectriques a haute et basse tension, v. 1, Paris, 1926; L о e w, Electrical Power Transmission, Ni w York, 1928; Lewis W. W., Transmission Line Engineering, N. Y., 1928; Dwight Η. B., Transmission Line Formulas, N. Y., 1925; Peek F. W., Dielectric Phenomena in High Voltage Engineering, N. Y., 1920; S t e i n m e t z С. P., Theory and Calculation of Transient Electric Phenomena a. Oscillations, N. Y., 1920; Riidenberg R., Elektrische Schalt-vorgange, 2 Auil., Berlin, 1926; Schwaiger A., Elektrische Festigkeitslehre, Berlin, 1925; Roth A., Hochspannungstechnik,Berlin,1927; Coombs R.D., Pole a. Tower Lines, New York, 1926; Pender H., Handbook for Electrical Engineers, 2 ed., New Yi.rk, 1922; Amer. Inst, of Electr. Eng. Standards, N. Y.; Vorschriftenbuch des V. D. E., Berlin, 1928; Peterson W. S. a. Cracker Η. I., Movements of Overhead Line Conductors during Short Circuits, «Transactions of the American Inst, of Electr. Eng.», N. Y., 1929, J; Symposium on Surge Voltage Investigation, ibid., 1928, 4; Lewis W. W., Relation between Transmission Line Insulation a. Transformer Insulation, ibid., 1928, 4; SpornP, Rationalisation of Transmission System Insulation Strength, ibid., 1928, 4; Clarke E., Steady State Stability in Transmission Systems, ibidem, 1926; Wagner C. F. a. Evans R. D., Static Stability Limits and the Intermediate Condenser Station, ibid., 1928, 1; Murray J. S. and RobertT., Power Limit Tests on Southeastern Power and Light Company’s System, ibid., 1929, 1. Л. Маш киллейсон.