> Техника, страница 58 > Логарифм

Логарифм

Логарифм, показатель степени, в к-рую нужно возвести основание (постоянное положительное число), чтобы получить данное число. Обозначив основание Л. через а. и Л. данного числа N через у, получаем¹ а^у=N,

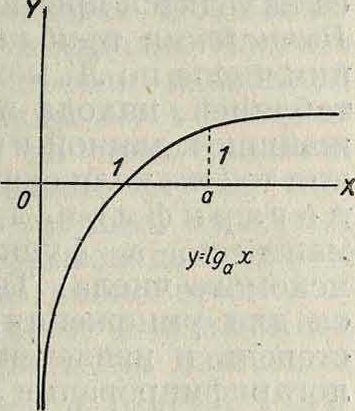
Свойства Л.: 1) Л. произведения равен сумме Л. сомножителей; 2) Л. дроби равен разности Л. числителя и знаменателя; 3) Л. степени равен показателю степени, умноженному налогарифм возводимого количества (корень рассматривается здесь как дробная степень); 4) Л. единицы равен нулю; 5) Л. основания равен 1. Обыкновенно предполагается а>1. Считая данное число ж переменным и обозначая его Л. через у, определяем логарифмическую ф-ию у=1д’_й х. Из определения Л. следует: х=а^у. Ф-ия а^у (степень с постоянным основанием и переменным показателем) называется показательной ф-ией. Она является обратной логарифмич. ф-ии. Ф-ия у=lg_e х определенна только для положительных значений ж (смотрите фигура); при а > 1 это ф-ия возрастающая, ее значения для ж < 1 отрицательны, для ж > 1 положительны,

lim ]g_a х=— со, Ит lg_a ж=+ со. х О×-* оо

Определение Л. для отрицательных и комплексных значений аргумента—см. Функции комплексного переменного.

Связь между Л. при различных основаниях. Пусть у=lg_aж, т.^ре. а^у=ж. Логарифмируем это равенство при основании Ь:

lg_bx=ylg_ba=lg_ax lg_ъа.

Отсюда при ж=b получаем:

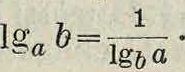
Производная логарифмич.ф-ии, см.Диф-ференциальнов исчисление.

Л. при основании

e=lim (l + Л ”=2,71828.

п -> оо называется натуральным и обозначается In x(lg_ex). Натуральные Л. являются в ряде вопросов анализа наиболее простыми,

X

к ним приводит вычисление J ~ и целого

1

ряда других интегралов (смотрите Интегральное исчисление).

Десятичные Л. При вычислениях обычно употребляются Л. с основанием 10. Такой Л. будем обозначать: lg х (lg_ln ж). Из определения Л. следует: lg 1=0, lg 10=1,

lg 100=2,., lg0,1--1, lg0,01=— 2,. Из свойства возрастания следует: десятичный Л. числа, заключенного между 1 и 10, имеет целую часть (характеристику Л.), равную 0, при 10 <-N<100 характеристика IgA⁷ равна!,и вообще, если число цифр до запятой есть к, то характеристика Л.= 7с—1. Дробная часть Л. называется мантиссой. Л. чисел, имеющих одинаковые значащие цифры, имеют одинаковые мантиссы. Таблицы десятичных Л. обыкновенно дают мантиссы для чисел от 100 до 999 (четырехзначные Л., то есть дающие приближенное значение мантиссы с 4 знаками) или от 1 000 до 9 999 (пятизначные Л.). Если число значащих цифр данного числа больше, чем дано в таблице, то мантисса находится при помощи интерполяции (смотрите Вычисления приближенные). Для нахождения числа по Л. можно пользоваться той же таблицей, находя в ней две мантиссы, ближайшие к данной, и применяя интерполяцию; для той же цели существуют таблицы антилогарифмов, где аргументом является мантисса, а функцией значащие цифры искомого числа. Таблицы Л. употребляются для умножения, деления, возведения в степень и извлечения корня из чисел; при логарифмировании эти действия заменяются соответственно более простыми—сложением, вычитанием, умножением и делением. Для многих других ф-ий (например тригонометрических) также часто даются значения не самих ф-ий, а их Л., для удобства последующих умножений и делений значений этих функций.

Имеются таблицы, которые дают возможность найти по Л. двух чисел Л. их суммы или разности. Предположим а>b; имеем:

lg (а + Ь)=lg а + lg- (1 + -* ) Обозначим

Iga - lg Ь=А, lg (l Т ц)=lg (l + 10^-А) =15.

Достаточно составить таблицу, дающую В как ф-июЛ, чтобы вычислить: lg (a+b)=lg а+Ь.

Аналогично: lg (а — b)=lg а + lg (1 — ^ или, принимая lg а — lg Ь=В, получаем: lg (a—b)==lga—lg положим lg ~₁₀__в=С, от куда 10"^B + 1(H^C=1. Имеем: lg (a—b)=lg a—С. Замечая, что В я С связаны симметричным соотношением, можем ограничиться таблицей, дающей значения В, при которых 10~^в <

В > 0,30103; для меньших значений нужно переменить роли В я С.

Для натуральных Л. существуют специальные таблицы. Но можно вычислять натуральные Л. по десятичным и обратно при помощи ф-лы:

Inх=lga: · In 10

или

lg ж=In ж · lge.

Число Μ=lg e=0,43429. называется модулем; число In 10= j^=~= 2,30259.

Ф-лы для вычисления Л.—см. Ряды, Вычисления приближенные.

Лит.: Успенский Я. В., Очерк истории логарифмов, Петроград, 1923; Пржевальск и и Е., Пятизначные таблицы логарифмов и тригонометрич. величин, М.—Л., 1928; Г он фен Б., Логарифмы и антилогарифмы в упрощенных таблицах, М., 1919; Афанасьев А. П., Таблицы математич. и физич. величин, П., 1923. В. Степанов.