> Техника, страница 58 > Логарифмическая линейка

Логарифмическая линейка

Логарифмическая линейка, прибор, служащий для производства вычислений, обычно совершаемых при помощи таблиц логарифмов. Пусть у=/(ж) представляет непрерывную однозначную функцию переменного ж, возрастающую в рассматриваемом промежутке изменения х. Составим таблицу значений этой функции для последовательного ряда обычно равноотстоящих значений аргумента и нанесем их на линейку в виде отрезков, имеющих общее начало. Против полученных т. о. точек надпишем соответствующие значения аргумента. То же самое проделаем по отношению к другой функции z=φ(ί) такого же рода, нанеся ее значения на другую линейку. Приложим две полученные нами шкалы одну к другой. Пусть начальная точка второй шкалы "совпадает с точкой х_х первой шкалы, а какая-нибудь ее точка ί с точкой ж₂; тогда очевидно наши шкалы могут служить для решения уравнения f(x_x) + φ( t)=(ж ₂) относительно одной из трех величин х_х, х₂, t по заданным двум. Предположим в частности, что обе функции и φ представляют логарифм. Уравнение примет вид:

lg х_х + lg t=lg ж₂,

откуда x_xt=Xz и ^х*=х_х, то есть наши линейки дают возможность находить произведение и частное двух чисел.

Построенная на этом принципе Л. л. имеет почти ту же давность, как и сами логарифмы. В 1620 г., через 6 лет после опубликования Непером его Mirifici Logaritlimorum Canonis Descriptio, Гюнтер предложил прибор, отличающийся от приведенной выше схемы лишь тем, что роль второй линейки играл циркуль, а еще 10 лет спустя Отред (Ought-red) воспользовался уже двумя линейками. С тех пор усовершенствовались лишь детали, пока в 1850 г. Мангейм не выработал того типа линейки, который с незначительными изменениями повторяется и сейчас целым рядом фирм: A. W. Faber, A. Nestler, W. F. Stanley, J. Davis, Gebr. Wichmann и др. Эта Л. л. (фигура 1) имеет две неподвижные шкалы У иА⁷!, между к-рыми перемещается подвижная часть ее (движок) с двумя

шкалами N и Νί, нанесенными на ее лицевой стороне, и тремя шкалами S, Т и L, нанесенными на ее обратной стороне. Шкала N делится на две равные части, каждая из которых принята за единицу дЛины и которые повторяют одна другую. На этих шкалах отложены отрезки, пропорциональные значениям логарифмов чисел от1 golO(lgl=0— начало шкалы, lg 10=1—конец шкалы), причем число промежуточных делений дается в зависимости от размеров Л. л.; так например на Л. л. в 25 сантиметров в промежутке от 1 до 2 деления даны через 0,02, в промежутке от 2 до 5—через 0,05 и в промежутке от 5 до 10—через 0,1. Шкала N тождественна

[ соответствующей множимому, начало шкалы Νί, на шкале Ν_χ против черты шкалы N[, соответствующей множителю, читаем произведение. В том случае когда множитель придется вне шкалы N_lt за этой последней надо вообразить ее повторение, иначе говоря, совместить с множимым на шкале N i конечную черту шкалы Νί и прочитать произведение на шкале Ν_χ против черты шкалы Ν{, соответствующей множителю. Число знаков п произведения, стоящих влево от запятой, как известно, или единицей меньше суммы числа знаков целой части множимого п₁ и множителя п₂ или равно этой сумме. Этим двум возможностям co

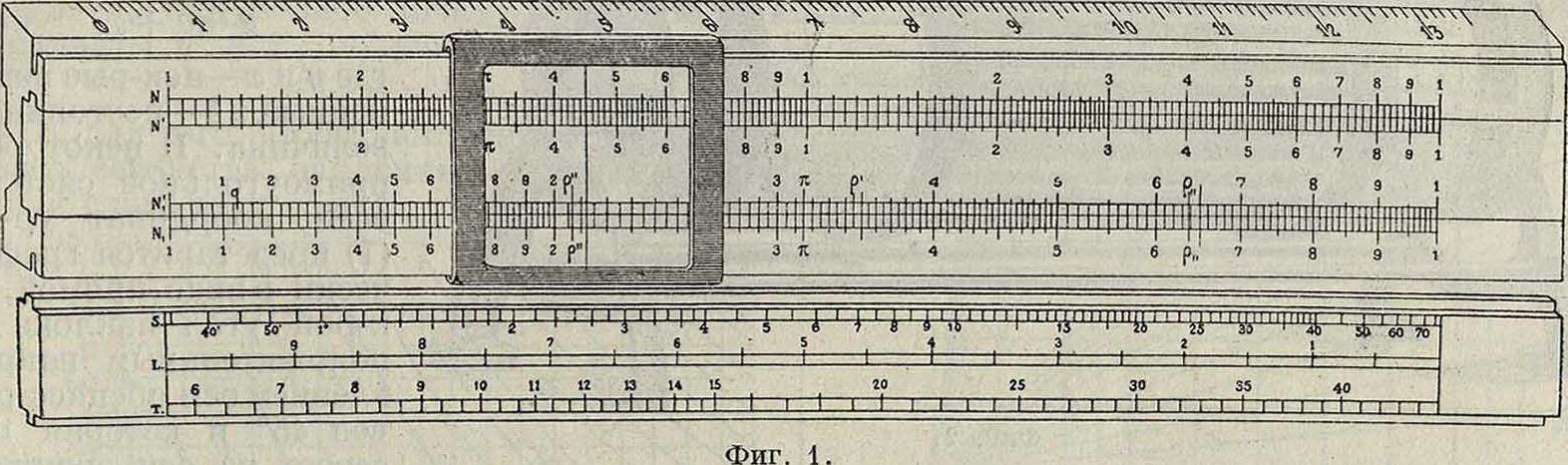
co шкалой N. Шкала N₁ повторяет одну из шкал N во вдвое большем масштабе и соответственно этому с более частыми делениями. Наконец шкала N{ тождественна со шкалой .NTj. Деления шкалы S соответствуют значениям 2 + lg sin х для значений х от 34 до 90° (sin 34^0,01 и следовательно lgsin34s=— 2, lg sin 90°=0) и отмечены значениями аргумента х; деления шкалы Т соответствуют значениям 1 + lg tg х для значений х от 5° 44 до 45° (tg 5° 44 as 0,1 и следовательно lg tg 5° 44 es — 1, lg tg 45°=0) и тоже отмечены значения аргумента х. Наконец шкала L дает значения логарифмов чисел. Л. л. снабжена визиром, состоящим из передвигающейся вдоль нее рамки со стеклом, на к-ром нанесены 1 или 3 перпендикулярные Л. л. черты. При трех чертах на визире обе крайние отстоят от средней на расстояние, равное lg * в масштабе шкалы N; это дает возможность, двигая одним визиром,

решать задачи типα= ~ и d

Визир облегчает оценку долей делений, дает возможность производить отсчеты по шкалам, не лежащим непосредственно одна около другой, и служит для фиксирования промежуточных результатов при сложных выкладках. При пользовании Л. л. надо помнить, что увеличение или уменьшение числа в 10, 100, 1 000,. раз не изменяет мантиссы логарифма числа, а влияет только на характеристику. Поэтому, с одной стороны, каждую из шкал N, N_x можно представить себе повторенной вправо и влево от фактически имеющейся шкалы,а с другой стороны, читать нанесенные на шкалах числа в зависимости от обстоятельств различно, например 2 можно читать как 0,2; 2; 20; 200 и т. д.

Умножение производится при помощи шкал N_x и N_l. Совмещая с чертой шкалы N_lt

ответствуют два случая отсчета произведения, а именно, при совмещении с множимым начала шкалы движка п=щ + n₂ —1, при совмещении конца шкалы п=щ + п_г. Деление производится на тех же шкалах, но теперь с чертой шкалы N_x, соответствующей делимому, совмещается черта шкалы Νί, соответствующая делителю. Частное читается на шкале Ν_χ против начальной или конечной черты шкалы Νί в зависимости от того, которая из них придется против шкалы Ν_χ. В первом случае число знаков целой части частного единицей больше разности числа знаков делимого и делителя, во втором оно равно этой разности. Возведение в квадрат и извлечение квадратного корня основано на известных соотношениях lg®^a=21ga; и lg j/ж=| lg®,

которые осуществляются шкалами N и N_x. Квадрат читается на шкале N против основания степени, отложенного на шкале N_x, обратно—корень квадратный—читается на шкале N_x против подкоренной величины, отложенной на шкале N. Комбинирование возвышения в квадрат с умножением и извлечения квадратного корня с делением дает возможность находить кубы и кубич. корни.

Назначение шкал S и Т двояко: во-первых, давать значения sin и tg в промежутках, указанных выше, во-вторых, производить вычисления, при которых sin и tg входят множителями и делителями. Действительно, совмещая начальные черты этих шкал с начальными чертами шкал N и N_x, имеем на этих последних против делений S я Т соответствующие значения sin и tg, причем первая половина N дает sin от 34 до 5° 44, вторая—от5° 44 до 90°. При вычислениях с sin и tg шкалами S и Т пользуются так же, как обычной логарифмич.шкалой, с тою только разницей, что шкале ввсегда соответству-

ет шкала N, а шкале Т—шкала Ν_τ. Более сложные вычисления требуют нахождения логарифмов чисел; для,этой цели служит шкала L обратной-стороны подвижной части линейки. Л. л. описанного типа изготовляются длиной 12,5, 25, 50 и даже 100 сантиметров и применяются в зависимости от требуемой точности. Допуская возможность отсчета до 0,1 миллиметров, получим для Л. л. в 25 сантиметров погрешность от 1,5 до 3%.

Наряду с описанным типом Л. л. постепенно выработался ряд Л. л. специального назначения. Прецизионная линей-к а при длине в 25 сантиметров дает точность Л. л. в 50 сантиметров благодаря тому, что на ней все шкалы разбиты пополам и каждая половина занимает всю длину Л. л. Прием вычисления при помощи этой Л. л. несколько сложнее, чем на обыкновенной Л. л. Далее изготовляются Л. л. со специальными шкалами, построенными по изложенному выше (в начале статьи) принципу и приспособленные для электротехнических, гидравлич., машиностроительных, железобетонных и других технических расчетов. Параллельно с разработкой и усовершенствованием Л. л. описанного типа делались попытки построения по тому же принципу других приборов в целях достижения или большей точности или большей компактности прибора. Из этих попыток заслуживают упоминания прибор Фуллера, дающий результат с точностью до 4 или даже 5 знаков, в к-ром шкала нанесена по винтовой линии на цилиндре и имеет длину свыше 25 м, и прибор Boucher, усовершенствованный Stanley, имеющий вид карманных часов, в к-ром шкалы нанесены на кон-центрич. вращающихся циферблатах и точность которого соответствует точности Л. л. в 25 см. В последнее время для более точных вычислений применяют т. н. счетные вальцы (Rechenwalzen), представляющие собой отдельные участки Л. л., нанесенные по образующим цилиндрич. вальца (фигура 2); движок в этом случае имеет форму полого цилиндра с окнами, прорезанными против основных шкал; деление движка нанесено по краям этих прорезов. Вальцы позволяют производить операции умножения и деления с такой же быстротой, как ичпри помощи обычной Л. л., но с точностью в 10—100 раз большей.

Лит.: Абрамов Η. М., Технич. вычисления, М., 1928; Павлов Η. Н., Производство технич. вычислений, 2 изд., М., 1927; Филиппов В. М., Теория и практика элементарных приближенных вычислений, СПБ, 1909; Франк М. Л., О решении трехчленных уравнений при помощи логарифмической линейки, «Сборн. ИИПС», Петроград, 1915, т. 89; Cajori F., Aj History of the Logarithmic Slide Rule, London, 1909; d’O c a g n e M., Le Calcul simplifid par les procedes mecaimpies et graphiques, 2 dd., Paris. 1905. К. Меликов»