> Техника, страница 58 > Логарифмические диагрammы

Логарифмические диагрammы

Логарифмические диагрammы, частный вид номограмм с неравными делениями шкал, когда деления последних пропорциональны логарифмам чисел, обозначающих точки деления (смотрите Номография). Построение Л. д. основывается на следующих принципах. Пусть имеется равенство

У=b + х, (1)

где у и х—нек-рые переменные, а b—постоянная величина. В некоторой прямоугольной системе осей координат ур-ие (1) представится графически в виде прямой, у которой угол наклона с положительным направлением оси абсцисс равен 45° и которая отсекает на оси ординат, считая от начала координат, отрезок, равный b. Меняя затем параметр b, придавая ему значения 6_1; Ь₂, ., Ь_п, получим семейство параллельных прямых, отсекающих на оси ординат отрезки Ь_г, Ь₂, ., b_п. Не трудно видеть, что, взяв на какой-либо из этих прямых у =b_v -f ж точку М с координатами ξ и η, имеем:

У=b_v + ξ. (2)

Т. о. для того, чтобы сложить при помощи полученной номограммы два числа ξ и b_v, нужно поступить след, образом. Взяв на оси Л точку, соответствующую числу ξ, про

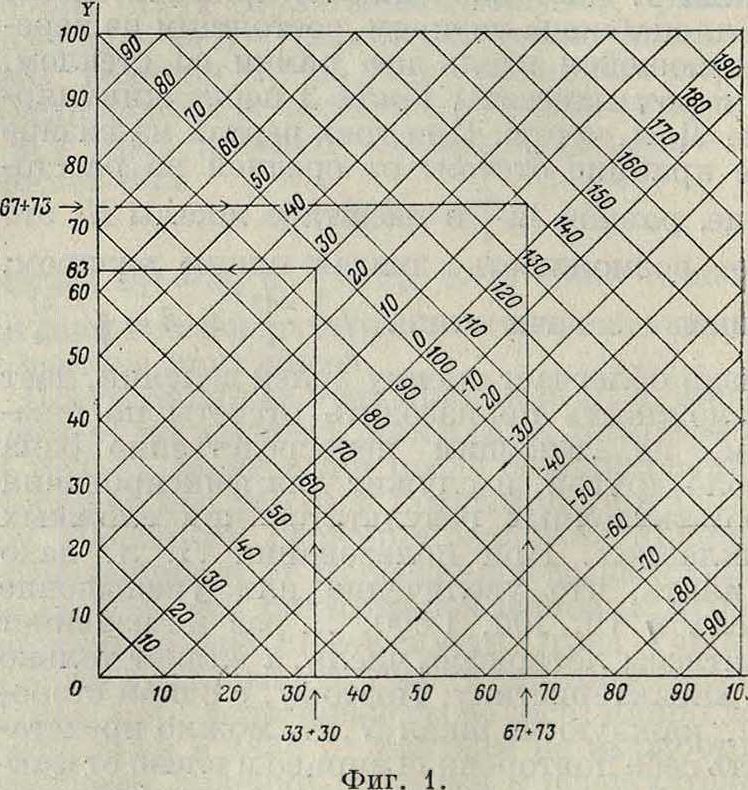
водят через эту точку перпендикуляр к оси×до встречи с наклонной (диагональной) прямой, имеющей параметр, равный другому слагаемому b_v, и затем из этой точки встречи опускают перпендикуляр на ось Y.

Число, соответствующее основанию этого перпендикуляра, при условии равенства масштабов делений осей координат, и дает искомую сумму (фигура 1). На практике обычно пользуются готовой сеткой, что освобождает от необходимости проведения вышеупомянутых перпендикуляров.

Если вместо (1) имеется равенство

у=b — х,	(3)
у + х=b,	(30

то при различных значениях’ b получаем семейство прямых, наклоненных к положительному направлению оси×под углом 135°. Взяв на какой-нибудь- из Этих прямых у+х= Ь„ какую-либо точку, имеющую координаты η и получим:

П + Г=b„. (4)

Т. о. для того, чтобы найти при помощи второго семейства наклонных прямых сумму двух слагаемых η и £, следует через точки

деления ξκη* на осях координат восставить к последним перпендикуляры и определить параметр b_v той наклонной прямой, которая проходит через точку пересечения перпендикуляров (фигура 1). Вычитание можно производить способами, обратными вышеуказанным.

Пусть имеется далее ур-ие:

, ху=а, (5)

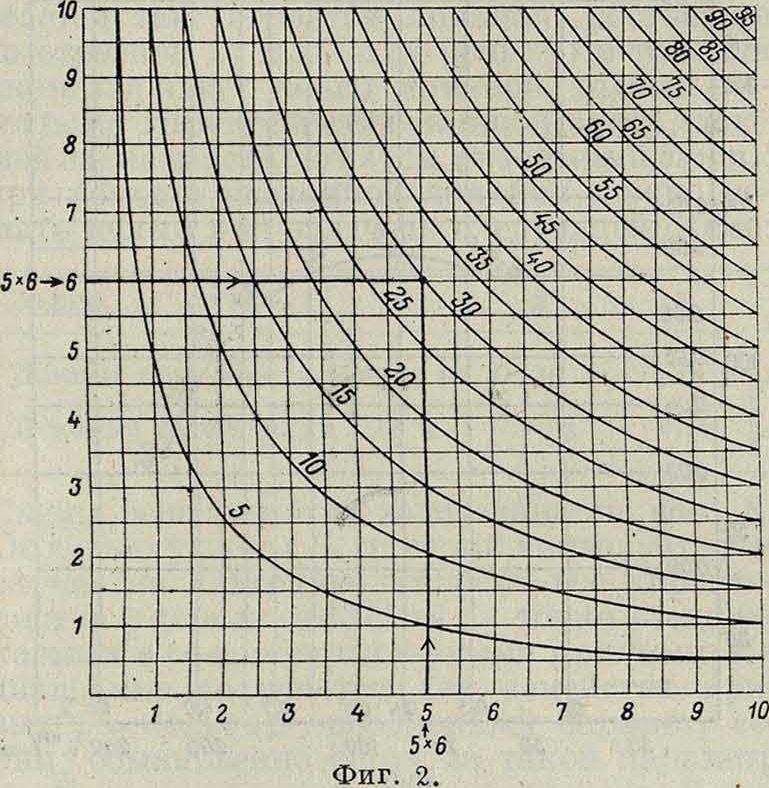
где х и у—попрежнему переменные, а а— постоянная величина. Графически ур-ие (5) представляется в прямоугольных координатах равнобокою гиперболою с асимптотами, совпадающими с осями координат. Меняя затем величину параметра а, придавая ему значения а_1г а₂, ., а_п, получим семейство равнобоких гипербол; при помощи этой номограммы можно производить умножения и деления чисел (фигура 2). Недостаток этой номограммы заключается в том, что если пересечение перпендикуляров не находится на одной из имеющихся на номограмме кривых, то приходится либо вычерчивать соответствующую новую кривую либо определять параметр последней наглаз, в ущерб конечно точности получаемых результатов. Для устранения указанного недостатка применяют номограмму, в которой кривые (гиперболы) заменены прямыми, проведение которых не представляет конечно таких затруднений, как проведение новых кривых. Пусть имеется равенство:

У=сю (6)

При определенном значении параметра а. равенство (6) [представляет прямую, прохо-

о i г i з * 5 е 7 a 9 ю

»3

Фигура 3.

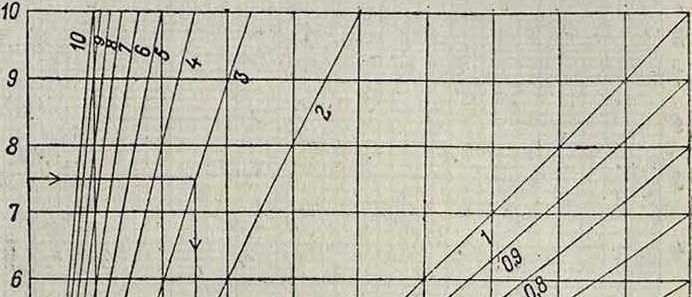
дящую через начало координат и тангенс угла наклона которой с положительным направлением оси×равен а. Меняя значения параметра а, получаем пучок прямых, проходящих через начало координат. Из (6) видно, что для того, чтобы умножить два числа х₁ и а_г, нужно взять на оси×точку, соответствующую числу х_и и провести через эту точку перпендикуляр к оси×до пересечения с наклонной прямой, имеющей параметр а_а; ордината полученной точки пере

сечения и определяет искомое произведение (фигура 3). Но, устраняя один недостаток (замена параметренных кривых прямыми), последняя номограмма обладает новыми недо-

статками, делающими ее мало пригодной для практич. применения и заключающимися в следующем: 1) если сомножители близко подходят к пределам а; и у номограммы, то точки пересечения выходят за пределы номограммы; так для того, чтобы умножить 10 на 10, необходимо, чтобы высота номограммы была в 10 раз больше ее основания;

2) пересечение прямых, перпендикулярных оси X, с наклонными прямыми, близко подходящими к оси Y, происходит под очень острым углом, вследствие чего делается почти невозможным б. или м. точное определение точки пересечения прямых; 3) в области, близкой к начальным значениям ж и у, имеет место скопление диагональных прямых, вследствие чего затрудняется отсчет.

Для того чтобы сохранить все преимущества прямолинейных номограмм и устранить в то же время вышеприведенные недостатки их, прибегают к Л. д., или логарифмическим номограммам, принцип построения которых заключается в следующем. Взяв логарифм от обеих частей (5), имеем равенство:

lg х + lg у=lg α, (7)

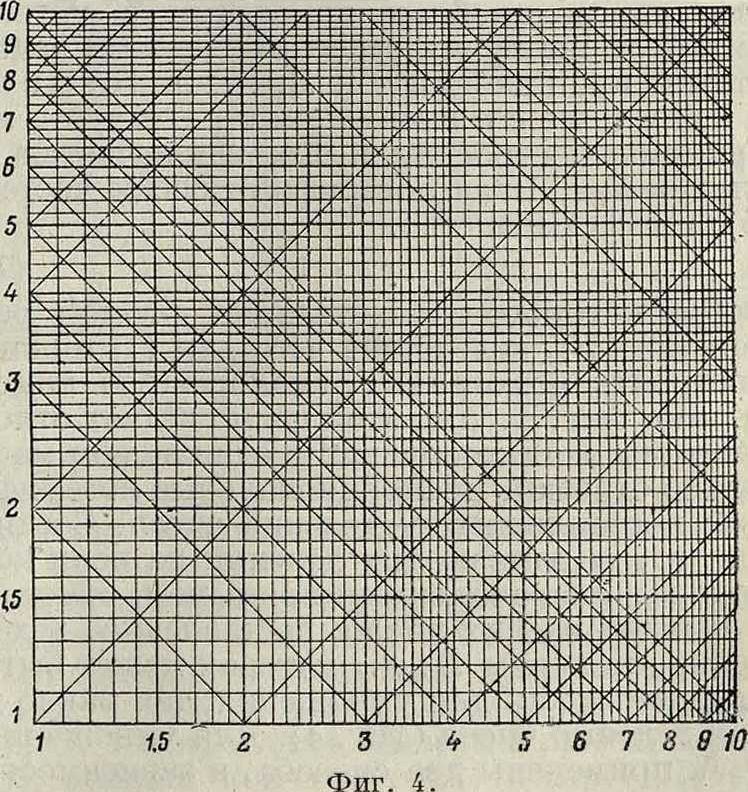
форма которого тождественна с формой равенства (3), вследствие чего для (7) можно построить номограмму, аналогичную номограмме фигура 1. Для этой цели следует отложить на осях координат в одинаковом масштабе отрезки, пропорциональные логарифмам поставленных у делений чисел. Соединив точки одинаковых делений на осях координат диагональными прямыми и отметив у каждой из них число, поставленное у деления, получим Л. д., которая может быть применена как для умножения, так равно и для деления чисел (фигура 4). Для умножения м. б. применены два способа, в зависимости от того, пользуются ли при этом диагональными прямыми, идущими под углом 45 или 135° к положительному направлению оси X. Умножение и деление, сведенные к сложению и вычитанию логарифмов, производят ся таким же образом, как это было описано выше для номограммы фигура 1.

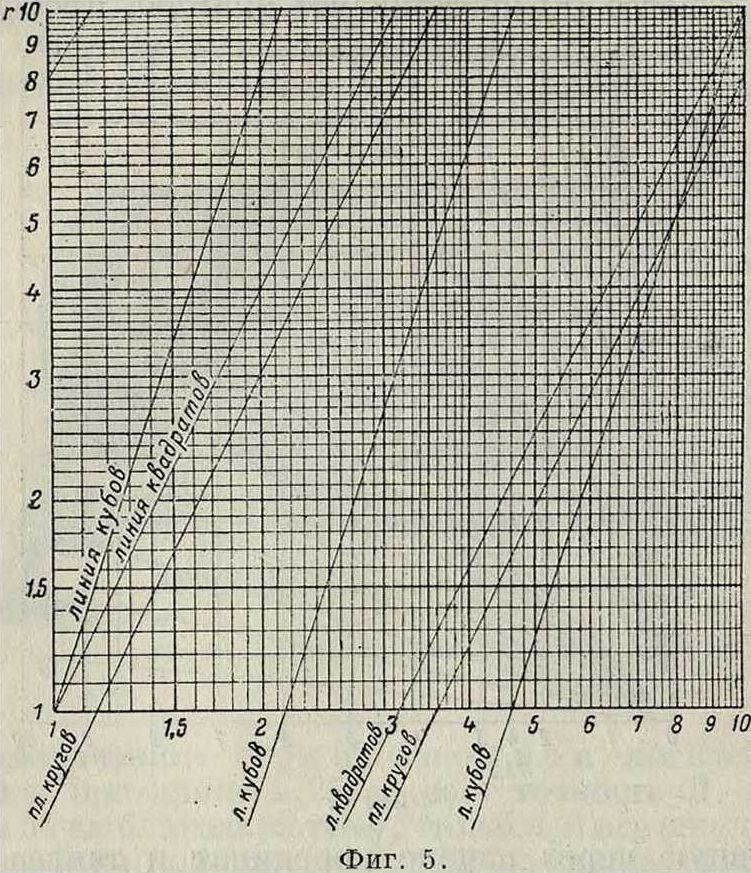
Л. д. очень удобны для получения ф-ий степени или корня какой-либо переменной, в особенности если степени и корни дробные. Ур-ие у=х³ например м. б. представлено еще и следующим образом: gy=Ά Igx, что имеет вид η=3ξ. Отсюда следует, что, проведя по сетке с логарифмич. делениями прямую через начало координат, имеющую тангенс угла наклона к положительному направлению оси×равный 3, получим т. н. линию кубов (фигура 5), то есть прямую, ординаты точек которой равны кубам соответствующих абсцисс. Для построения линии кубов достаточно верхнее и нижнее основания квадратной Л. д. разделить на три равные части и соединить точки деления 0, 1, 2 нижнего основания соответственно с точками деления 1, 2, 3 верхнего основания. Аналогично можно построить линию любой степени п,

ΊΡ

300

rn·

50-

30 SO W 100 ZOO ООО v "Уччс

Фигура 6.

независимо от того, будет ли п числом целым или дробным. Во всех случаях тангенс угла наклона диагональных прямых должен равняться п. Л. д. применяются во многих областях техники, как например в сопротивлении материалов, деталях машин, электротехнике и т. д. Примером Л. д. служат диаграммы для расчета винтов аэропланов.

Лит.: Астафьев А., Применение методов номографии, СПБ,1909; Волков А., Математические основания номографии, М.,1911;Герсеванов Н., Основания номографич. исчисления, выи. 1, СПБ, 1906. вып. 2, СПБ, 1908; Педл Дж., Построение и применение номограмм, Москва, 1913; M e h m k е R., Numerisches Rechiien, Enzyklopadie d. mathemat. Wissenschaften, В. 1, T.2, H. 6—7, B.—Lpz., 1901 — 02, p. 1006—1052; M e h m к e R., Neue Methode be-liebige numerische Gleichungen mlt einer Unbekannten graphisch aufzulosen, «Civilingenieur», B. 1889; Reuse h 1 e C., Graphisch-meehanischeMethode z. Auflosung d. numerischen Gleichungen, Stuttgart, 1884; Schilling F., tlber d. Nomographie von M. d’Ocagne. Lpz., 1917; G о e d s e e 1 s, Les proc6d6s pour simplifier les calculs, Bruxelles, 1898; d0 cagne M., Traitdde nomographie, 2 6d., P., 1899; d’O c a g n e M., Le calcul simplifid par les proc6d6s niecaniques et graphiques, P., 1905; d’0 cagne M., Calcul gra-phi que et nomographie, P., 1910; Soreau R., Contribution a la thOorie et aux applications de la nomographie, «Mdmoirs et comptes rendus des travaux de la Socifitedesingen.civils de France»,?., 1901;Pesci G., Cenni di nomogralia, Livorno, 1901. M- Серебренников.

Логарифмические диаграммы в авиации широко применяются как для расчета винтов, так и аэропланов; они предложены сотрудником лаборатории Эйфеля Ритом (Rith). Винтовые Л. д. строят на лога-рифмич. бумаге, откладывая по осям с ло-гарифмич. шкалами координаты:

₀ 75 · 603. N „, 60 V

ρη^ΙΠ ^{и λ}~ 3,6 1ГБ’

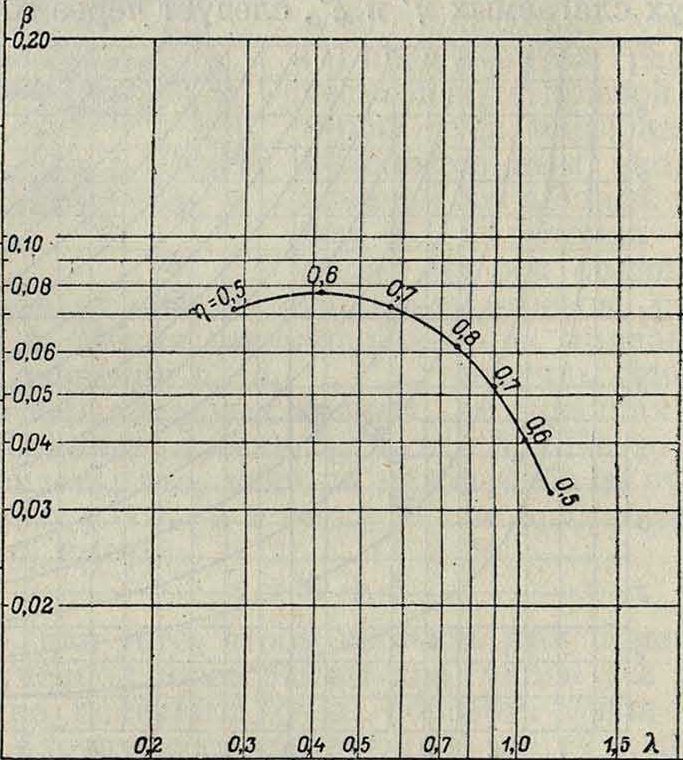
где N—мощность в 1Р, п—число оборотов винта в мин., Ώ—диаметр его в м, v—скорость в км/ч, ρ—массовая плотность среды в килограммах ск²/м“ (фигура 6). На полученной кривой делают разметку величин кпд η. Взяв некоторые средние практические величины для n, D и ρ, на шкалах λ и β наносят параллельные шкалы v и Ν. На той же номограмме наносят шкалы ддя п и Ώ с наклонами ³/ι и 6/j к шкале λ (v) (фигура 7). На этих шкалах особо выделяют точки с отметками п и Ώ, принятые за средние, и обозначают знаком Or (origine—начало). Расчет по Л. д. ведется так: строится ломаная, состоящая из отрезков v, n, D и N (фигура 7) в том или ином порядке; конец ломаной должен лежать на характеристич. кривой винта, дающей зависимость β от λ (смотрите Воздушный винт); при помощи указанной ломаной можно решать целый ряд задач по следующей схеме:

ра получим п и η при скорости v. Тяга вычисляется по ф-ле:

ф ₌ 75 3,6 п N _

Взяв несколько скоростей v, получают полную характеристику винтомоторной группы. Характеристики для высоты г получаются так же, но на характеристике мотора откладывают фиктивные мощности Νφ.=^, где

А—отношение плотностей на высоте ζ и на земле. Таким путем исследуются все вопро-1 г з * ь

Фигура 8.

сы, связанные с изучением работы винтомоторной группы.

Логарифмические поляры аэро,-планов строятся на основании ур-ий:

зУ³’

Задача.	1	2	3	4	5
Данные величины.	N, v, п	D, v, п	N_y D, n	N, D, v	N, D, v
Искомые величины.	D, η	Ν, η	V, η	П, η	n, V

Схемы решения этих задач даны на фигуре 8. Особенно удобны Л. д. серии винтов. В этом случае на диаграмму наносят все характеристич. кривые семейства, и точки с одинаковыми η соединяют плавными кривыми. На диаграмме получается два семейства кривых р=Const (р—переменный параметр серии; обыкновенно берут за такой параметр Л=~, где Н—шаг винта) и η=Const. Имея такую диаграмму, легко для определенного задания (обычно N, п, v) подобрать винт с наибольшим у, меняя длину отрезка Ώ (или п) таким образом, чтобы он касался одной из кривых η=Const в своей конечной точке. В этой точке получим D, р и η для наилучшего винта. Для построения характеристики винтомоторной группы (смотрите Аэродинамика) аэропланов берут винтовую Л. д. (фигура 9); на особом куске кальки Т проводят ось v, а затем из произвольной точки ее а ведут отрезок ab D; через точку Ь проводят линию, параллельную шкале п, и размечают на ней числа оборотов γι. Из полученных точек откладывают отрезки Ν, взятые из характеристики мотора, в масштабе шкалы Ν. Кривая МК дает логарифмич. характеристику мотора. Совмещая точку а кальки с любой етметкой ν на диаграмме, в точке пересечения А характеристик винта и мото где G—вес самолета в килограммах, N— потреби, мощность в IP, S—площадь крыльев в м², ρ—массовая плотность среды в килограммах ск²/м·, ν—скорость самолета в км/ч, С_у и С_х—коэфициенты подъемной, силы и лобового сопротивления (смотрите Аэродинамика) аэропланов. По осям логарифмической бумаги наносятся шкалы R_x и R_y на тех же осях наносятся параллельные шкалы N и G, получаемые из предыдущих формул при определенном v—v₁. На этой же номограмме наносят шкалы ν и п (фигура 10) с наклонами ²/₃ и 1 по

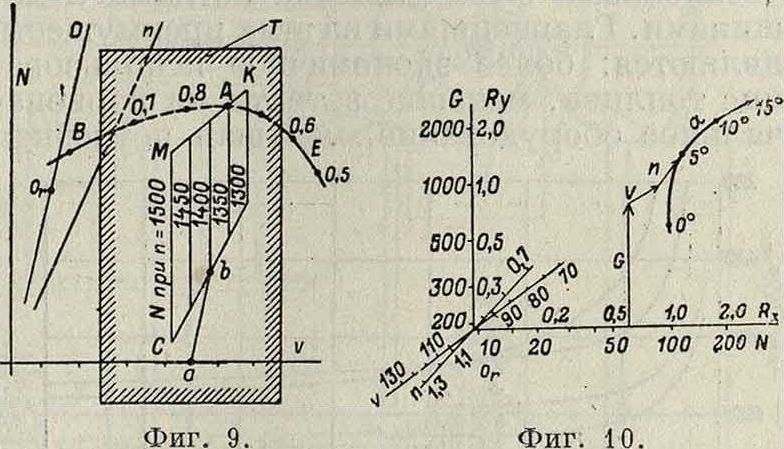
отношению к оси R_x (N), на шкалах выделяют точки г>=·υ_χ и п=1, отмечая их знаком Or. Нанося кривую R_y в зависимости от R_x и отмечая на ней углы атаки а°, получим логарифмическую поляру аэроплана. Шкала п служит для исследования влияния подобного изменения крыльев самолета в и раз. Ломаная линия из отрезков N, G, ν и п, откладываемых в любом порядке, должна кончаться на поляре. Путем, аналогичным описанному выше, решается ряд задач при трех заданных и двух искомых величинах из числа пяти переменных N, G, n, v и а и ряд задач, связанных с изменением масштаба п. Таким же путем

решается ряд задач о минимуме тяги, мощности, максимуме скорости и тому подобное. Влияние высоты полета г легко. учитывается при помощи шкалы п: уменьшение плотности в п раз равносильно уменьшению размеров самолета в Vn раз. Можно прямо по шкале п разбить шкалу высоты полета г. Характеристика винтомоторной группы позволяет построить на той же диаграмме кривые полезных мощностей (фигура 11) на любой высоте. Перенося поляру самолета на отрезок G вниз получим кривую МР; в месте касания этой кривой с одной из кривых полезных мощностей получим режим потолка.

Лит.: Юрьев Б. Н., Воздушные гребные винты, «Труды ЦАГИ», Москва, 1925, вып. 10; В е т-чинкин В. П., Теория гребных винтов, Москва, 1926; В е т ч и н к и н В., Каменев С., Ченцов Н., Динамика полетов, «Труды ЦАГИ», Москва, 1927, вып. 26. В. Ведров.